四、查找算法
文章目录
- 一、查找算法介绍
- 二、线性查找算法
- 2.1 顺序查找
- 2.2 二分查找(折半查找)
- 2.3 插值查找
- 2.4 斐波拉契(黄金分割法)查找算法
- 三、树表的查找
- 3.1 二叉排序树
- 3.1.1 引入
- 3.1.2 基本介绍
- 3.1.3 二叉树的遍历
- 3.1.4 二叉树的删除
- 3.2 平衡二叉树
- 3.2.1 基本介绍
- 3.2.2 左旋转(对应RR型)
- 3.2.3 右旋转(对应LL型)
- 3.2.4 双旋转(对应LR型和RL型)
- 3.3 B树
- 3.3.1 引入
- 3.3.2 B树的基本介绍
- 3.3.3 2-3树
- 3.3.4 B树、B+树和B*树
- 四、散列(哈希)表
- 4.1 散列(哈希)表引出
- 4.2 散列(哈希)表的基本介绍
- 4.3 散列(哈希)表 --- 应用实例
一、查找算法介绍

二、线性查找算法
2.1 顺序查找

package com.gyh.search;/*** @author Gao YongHao* @version 1.0*/
public class SeqSearch implements Search<Integer> {public static void main(String[] args) {Integer arr[] = {1, 9, 11, -1, 34, 89};int index = new SeqSearch().search(arr, -1);System.out.println(index);}@Overridepublic int search(Integer[] nums, Integer value) {for (int i = 0; i < nums.length; i++) {if (nums[i].equals(value)) {return i;}}return -1;}
}2.2 二分查找(折半查找)


package com.gyh.search;import java.util.ArrayList;/*** @author Gao YongHao* @version 1.0* <p>* 注意:使用二分查找的前提是 该数组是有序的*/
public class BinarySearch implements Search<Integer> {public static void main(String[] args) {Integer[] arr = {-1, 11, 11, 11, 34, 89};BinarySearch binarySearch = new BinarySearch();int index = binarySearch.search(arr, 11);System.out.println(index);ArrayList<Integer> integers = binarySearch.searchAll(arr, 11);integers.forEach(System.out::println);}@Overridepublic int search(Integer[] nums, Integer value) {if (nums[0] > value || nums[nums.length - 1] < value) {return -1;}return search(nums, value, 0, nums.length - 1);}private int search(Integer[] nums, int value, int left, int right) {if (left > right) {return -1;}int mid = (left + right) / 2;if (nums[mid] < value) {return search(nums, value, mid + 1, right);} else if (nums[mid] > value) {return search(nums, value, left, mid - 1);} else {return mid; // 只返回一个值的写法}}@Overridepublic ArrayList<Integer> searchAll(Integer[] nums, Integer value) {if (nums[0] > value || nums[nums.length - 1] < value) {return new ArrayList<>();}return search2(nums, value, 0, nums.length - 1);}private ArrayList<Integer> search2(Integer[] nums, int value, int left, int right) {if (left > right) {return new ArrayList<>();}int mid = (left + right) / 2;if (nums[mid] < value) {return search2(nums, value, mid + 1, right);} else if (nums[mid] > value) {return search2(nums, value, left, mid - 1);} else {/*** 思路分析* 1. 在找到 mid 索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足 等于value的元素下标加入到集合 ArrayList中* 3. 向 mid 索引值的右边扫描,将所有满足 等于value的元素下标加入到集合 ArrayList中*/ArrayList<Integer> integers = new ArrayList<>();int temp = mid - 1;while (temp >= 0 && nums[temp].equals(nums[mid])) {integers.add(temp--);}integers.add(mid);temp = mid + 1;while (temp <= nums.length - 1 && nums[temp].equals(nums[mid])) {integers.add(temp++);}return integers;}}
}2.3 插值查找


package com.gyh.search;import java.util.ArrayList;/*** @author Gao YongHao* @version 1.0*/
public class InsertSearch implements Search<Integer> {public static void main(String[] args) {Integer[] arr = {-1, 11, 11, 11, 34, 89};InsertSearch insertSearch = new InsertSearch();int index = insertSearch.search(arr, 11);System.out.println(index);}@Overridepublic int search(Integer[] nums, Integer value) {return search(nums, value, 0, nums.length - 1);}private int search(Integer[] nums, int value, int left, int right) {// 注意:value < nums[0] 和 value > nums[nums.length -1 ] 的条件必须有// 否则得到的mid值可能越界(如value比nums的最大的数大得多 ...)if (left > right || value < nums[left] || value > nums[right]) {return -1;}// 自适应的midint mid = left + (value - nums[left]) / (nums[right] - nums[left]) * (right - left);if (nums[mid] < value) {return search(nums, value, mid + 1, right);} else if (nums[mid] > value) {return search(nums, value, left, mid - 1);} else {return mid; // 只返回一个值的写法}}}2.4 斐波拉契(黄金分割法)查找算法



package com.gyh.search;
import java.util.Arrays;/*** @author Gao YongHao* @version 1.0*/
public class FibonacciSearch implements Search<Integer> {private static final int MAX = 20;public static void main(String[] args) {Integer[] arr = {-1, 11, 11, 11, 34, 89};FibonacciSearch fibonacciSearch = new FibonacciSearch();int index = fibonacciSearch.search(arr, -1);System.out.println(index);}@Overridepublic int search(Integer[] nums, Integer value) {int low = 0;int high = nums.length - 1;int k = 0; // 表示斐波拉契分割数值的下标int mid = 0; // 表示存放mid值int[] f = fib(); // 获取到斐波拉契数列// 获取到斐波那契分割数值的下标while (high > f[k] - 1) {k++;}// 因为 f[k] 值可能大于 nums 的长度,因此我们需要使用Arrays类,构造一个新的数组,并指向a[]// 不足的部分会使用 0 填充Integer[] temp = Arrays.copyOf(nums, f[k]);// 实际上需求使用 nums 数组最后的数填充 temp// 只需要对总数据作一次填充即可for (int i = high + 1; i < temp.length; i++) {temp[i] = nums[high];}// 与二分查找类似使用while数组处理,找到我们的数 keywhile (low <= high) {mid = low + f[k - 1] - 1; // 黄金分割点位置if (value < temp[mid]) { // 我们应该继续向左继续向数组的前面查找high = mid - 1;/*** 为什么 k--* 说明* 1. 全部元素 = 前面的元素 + 后面的元素* 2. f[k] = f[k-1] + f[k-2]* 因为 前面的有 f[k-1] 元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]* 即 在前面的f[k-1]继续查找 k--* 即 下次循环 mid = low + f[k-1-1]-1*/k--;} else if (value > temp[mid]) {low = mid + 1;/*** 为什么是 k-=2* 说明* 1. 全部元素 = 前面的元素 + 后面的元素* 2. f[k] = f[k-1] + f[k-2]* 3. 因为后面我们有f[k-2]个数所以可以继续拆分 f[k-2] = f[k-3] + f[k-4]* 4. 即在后面的f[k-2]继续查找 k-=2* 5. 即下次循环 mid = low + f[k-1-2]-1*/k -= 2;} else { // 找到// 需要确定,返回的是哪个下标// 存在最终定位的 mid 是由原数组最大值扩充的元素return Math.min(mid, high);}}return -1;}private int[] fib() {int[] fs = new int[MAX];for (int i = 0; i < MAX; i++) {if (i == 0 || i == 1) {fs[i] = 1;continue;}fs[i] = fs[i - 1] + fs[i - 2];}return fs;}}三、树表的查找
3.1 二叉排序树
3.1.1 引入


3.1.2 基本介绍

3.1.3 二叉树的遍历

package com.gyh.tree;/*** @author Gao YongHao* @version 1.0*/
public class BinarySortTree {public static void main(String[] args) {int[] arr = {7, 3, 10, 12, 5, 1, 9};BNode binarySortTree = new BinarySortTree().createBinarySortTree(arr);new BinarySortTree().midOrder(binarySortTree);}public void midOrder(BNode node) {if (node == null) {return;}midOrder(node.left);System.out.println(node.n);midOrder(node.right);}public BNode createBinarySortTree(int[] arr) {if (arr == null || arr.length <= 0) {return null;}BNode root = new BNode(arr[0]);BNode tNode;for (int i = 1; i < arr.length; i++) {tNode = root;while (true) {if (arr[i] < tNode.n) {if (tNode.left == null) {tNode.left = new BNode(arr[i]);break;} else {tNode = tNode.left;}} else {if (tNode.right == null) {tNode.right = new BNode(arr[i]);break;} else {tNode = tNode.right;}}}}return root;}
}class BNode {int n;BNode left;BNode right;public BNode(int n) {this.n = n;}public BNode(int n, BNode left, BNode right) {this.n = n;this.left = left;this.right = right;}
}
3.1.4 二叉树的删除
- 主要思想:
- 前提是 需要有指向
当前结点与其双亲结点的变量 - 若当前结点是叶子结点,直接删除
- 若当前结点的孩子结点只有一个(左或右),将当前结点的左(右)孩子赋给双亲结点的指向当前结点的变量(
parent.left或parent.right) - 若当前结点的孩子结点有两个,则使用当前结点的
右子树的中最小值对应的结点填充到这个位置(再该填充值原来的位置的结点); 或使用当前结点的左子树的中最大值对应的结点填充到这个位置(再该填充值原来的位置的结点)

package com.gyh.tree;/*** @author Gao YongHao* @version 1.0*/
public class BinarySortTree {private BNode root;public static void main(String[] args) {int[] arr = {7, 3, 10, 12, 5, 1, 9};BNode binarySortTree = BinarySortTree.createBinarySortTree(arr);new BinarySortTree(binarySortTree).midOrder();new BinarySortTree(binarySortTree).remove(7);new BinarySortTree(binarySortTree).midOrder();}public BinarySortTree(BNode root) {this.root = root;}public void midOrder() {midOrder(root);}private void midOrder(BNode bn) {if (bn == null) {return;}midOrder(bn.left);System.out.println(bn.n);midOrder(bn.right);}// 查找要删除的结点private BNode search(BNode bn, int value) {if (bn == null) {return null;}if (value < bn.n) {return search(bn.left, value);} else if (value > bn.n) {return search(bn.right, value);} else {return bn;}}// 查找要删除结点的父节点private BNode searchParent(BNode bn, int value) {if ((bn.left != null && bn.left.n == value) || (bn.right != null && bn.right.n == value)) {return bn;} else {if (value < bn.n && bn.left != null) {return searchParent(bn.left, value); // 向左子树寻找} else if (value > bn.n && bn.right != null) {return searchParent(bn.right, value); // 向右子树寻找} else {return null;}}}public void remove(int value) {remove(root, value);}public void remove(BNode bn, int value) {// 1、寻找要删除的结点BNode node;if (root == null || (node = search(bn, value)) == null) {return;}// 2、寻找要删除的结点的父结点BNode pNode = searchParent(root, value);// 若是叶子结点则直接删除后,重置其父节点的指向if (node.left == null && node.right == null) {if (pNode == null) {// 删除根节点信息并退出root = null;return;}if (pNode.left == node) {pNode.left = null;} else {pNode.right = null;}} else if (node.left == null) { // 若只有一棵子树if (pNode == null) {// 删除根节点root = node.right;return;}if (pNode.left == node) {pNode.left = node.right;} else {pNode.right = node.right;}} else if (node.right == null) {if (pNode == null) {// 删除根节点root = node.left;return;}if (pNode.left == node) {pNode.left = node.left;} else {pNode.right = node.left;}} else { // 有两棵子树// 方式一:找左子树的最大值(最右的结点)
// BNode lNode = node.left;
// while (lNode.right != null) {
// lNode = lNode.right;
// }
// // 删除左边的最大值点
// remove(node, lNode.n);
// // 将左边的最大值赋给当前结点
// node.n = lNode.n;// 方式二:找右子树的最小值(最最的结点)BNode rNode = node.right;while (rNode.left != null) {rNode = rNode.left;}// 删除右边的最小值点remove(node, rNode.n);// 将右边的最小值赋给当前结点node.n = rNode.n;}}public static BNode createBinarySortTree(int[] arr) {if (arr == null || arr.length <= 0) {return null;}BNode root = new BNode(arr[0]);BNode tNode;for (int i = 1; i < arr.length; i++) {tNode = root;while (true) {if (arr[i] < tNode.n) {if (tNode.left == null) {tNode.left = new BNode(arr[i]);break;} else {tNode = tNode.left;}} else {if (tNode.right == null) {tNode.right = new BNode(arr[i]);break;} else {tNode = tNode.right;}}}}return root;}
}class BNode {int n;BNode left;BNode right;public BNode(int n) {this.n = n;}public BNode(int n, BNode left, BNode right) {this.n = n;this.left = left;this.right = right;}
}3.2 平衡二叉树

3.2.1 基本介绍
- 平衡二叉树的平衡调整方法
在插入结点时,首先按照二叉排序树处理,若插入结点后破坏了平衡二叉树的特性,需要对平衡二叉树进行调整。调整方法是:找到离插入结点最近且平衡因子绝对值超过1的祖先结点,以该结点为根的子树称为最小不平衡子树,可将重新平衡的范围局限于这棵树。

3.2.2 左旋转(对应RR型)


3.2.3 右旋转(对应LL型)

3.2.4 双旋转(对应LR型和RL型)


package com.gyh.tree;/*** @author Gao YongHao* @version 1.0* <p>* 平衡二叉树*/
public class BalancedBinaryTree {public static void main(String[] args) {int[] arr = {4, 3, 6, 5, 7, 8};BBNode binarySortTree = BalancedBinaryTree.createBinarySortTree(arr);BalancedBinaryTree.midOrder(binarySortTree);System.out.println("树的高度:" + BalancedBinaryTree.height(binarySortTree));System.out.println("树的左子树高度:" + BalancedBinaryTree.leftHeight(binarySortTree));System.out.println("树的右子树高度:" + BalancedBinaryTree.rightHeight(binarySortTree));}// RR 型对应左旋转public static void leftRote(BBNode root) {// 创建一个新节点,以当前根节点的值BBNode bbNode = new BBNode(root.d);// 把新的结点的左子树根节点值设置成当前结点的左子树根节点值bbNode.left = root.left;// 把新的结点的右子树节点值设置成当前结点的右子树的左子树节点值bbNode.right = root.right.left;// 把当前结点的值替换为右子树节点值root.d = root.right.d;// 把当前结点的右子树设置为右子树的右子树节点值root.right = root.right.right;// 把当前结点的左子树设置为新节点root.left = bbNode;}// LL型对应右旋转private static void rightRote(BBNode root) {BBNode bbNode = new BBNode(root.d);bbNode.right = root.right;bbNode.left = root.left.right;root.d = root.left.d;root.left = root.left.left;root.right = bbNode;}public static void midOrder(BBNode bn) {if (bn == null) {return;}midOrder(bn.left);System.out.println(bn.d);midOrder(bn.right);}// 计算平衡因子private static int avlFactor(BBNode bbn) {return leftHeight(bbn) - rightHeight(bbn);}// 平衡化过程// 本例中并没有寻找最小不平衡子树,直接对根进行平衡化操作(此操作过程有误,仅实验方法)private static void avl(BBNode root) {if (root == null) {return;}// 计算左子树高 和 右子树高int avlFactor = avlFactor(root);int leftAvlFactor;if (root.left == null) {leftAvlFactor = 0;} else {leftAvlFactor = avlFactor(root.left);}int rightAvlFactor;if (root.right == null) {rightAvlFactor = 0;} else {rightAvlFactor = avlFactor(root.right);}if (avlFactor == -2 && rightAvlFactor == -1) { // 需要左旋转leftRote(root);}if (avlFactor == -2 && rightAvlFactor == 1) { // 先右后左旋转rightRote(root.right);leftRote(root);return;}if (avlFactor == 2 && leftAvlFactor == 1) { // 需要右旋转rightRote(root);return;}if (avlFactor == 2 && leftAvlFactor == -1) { // 需要左后右旋转leftRote(root.left);rightRote(root);}}public static BBNode createBinarySortTree(int[] arr) {if (arr == null || arr.length <= 0) {return null;}BBNode root = new BBNode(arr[0]);BBNode tNode;for (int i = 1; i < arr.length; i++) {tNode = root;while (true) {if (arr[i] < tNode.d) {if (tNode.left == null) {// 添加新值tNode.left = new BBNode(arr[i]);// 平衡化处理avl(root);break;} else {tNode = tNode.left;}} else {if (tNode.right == null) {tNode.right = new BBNode(arr[i]);// 平衡化处理avl(root);break;} else {tNode = tNode.right;}}}}return root;}public static int leftHeight(BBNode bbn) {return height(bbn.left);}public static int rightHeight(BBNode bbn) {return height(bbn.right);}public static int height(BBNode bbn) {if (bbn == null) {return 0;}return Math.max(height(bbn.left), height(bbn.right)) + 1;}
}class BBNode {int d;BBNode left;BBNode right;public BBNode(int d) {this.d = d;}
}
3.3 B树
3.3.1 引入


3.3.2 B树的基本介绍
- 定义见书上 P210

3.3.3 2-3树
- 3阶(阶数代表
最大分叉数)的B树,至多可有两个关键字,至少有一个关键字(即子树个数为2或者3,故成为2-3树)


- 插入时的分裂方法参见书 P214

3.3.4 B树、B+树和B*树

-
B树

-
注意:对B树数据存放位置的描述(可能存在于
叶子结点与非叶子结点) -
B+树

-
注意:对B+树数据存放位置的描述(只存在于
叶子结点) -
B*树

四、散列(哈希)表
4.1 散列(哈希)表引出

4.2 散列(哈希)表的基本介绍

4.3 散列(哈希)表 — 应用实例

package com.gyh.search;import java.util.HashMap;
import java.util.Objects;/*** @author Gao YongHao* @version 1.0*/
@SuppressWarnings("all")
public class HashTableDemo<K, V> {public static void main(String[] args) {HashTableDemo<Integer, Emp> hashTab = new HashTableDemo<Integer, Emp>();hashTab.put(1, new Emp(1, "aa", 1, 12, "zg"));hashTab.put(1, new Emp(1, "bb", 1, 12, "33"));hashTab.put(1, new Emp(1, "dd", 1, 12, "dd"));hashTab.put(101, new Emp(101, "cc", 1, 12, "55"));System.out.println(hashTab.get(1));}// 数组private Node<K, V>[] table;// 设置最大的容量private static int MAX = 100;private int size = 0;// 不考虑扩容public HashTableDemo() {table = (Node<K, V>[]) new Node[MAX];}public void put(K k, V v) {putVal(hash(k), k, v);}public V get(K k) {
// HashMapint hash;Node<K, V> n, e;if (size > 0 && (e = table[hash = hash(k)]) != null) {// 遍历位于同一位置的单链表上的元素while (e != null) {if (hash == e.hash && (k == e.k || k.equals(e.k))) {return e.v;}e = e.next;}}return null;}private void putVal(int hash, K k, V v) {Node<K, V> cur, p;// 该位置没有初始的数值if ((cur = table[hash]) == null) {table[hash] = new Node<>(hash, k, v, null);size++;} else { // 遍历链表中的元素。相等则值替换,不等则直接添加至最后while (cur != null) {if (hash == cur.hash && (k == cur.k || k.equals(cur.k))) {// 表示相同则值替换cur.v = v;break;}// 若是最后一个元素则添加if ((p = cur.next) == null) {cur.next = new Node<>(hash, k, v, null);size++;break;} else {cur = p;}}}}// 散列函数计算存储的位置(除留余数法)private int hash(K v) {int h = v.hashCode();return h % MAX;}}class Node<K, V> {int hash;K k;V v;Node<K, V> next;public Node(int hash, K k, V v, Node<K, V> next) {this.hash = hash;this.k = k;this.v = v;this.next = next;}
}class Emp {private int id; // 雇员的Idprivate String name; // 名字private int gender; // 性别private int age; // 年龄private String address; // 地址public Emp() {}@Overridepublic String toString() {return "Emp{" +"id=" + id +", name='" + name + '\'' +", gender=" + gender +", age=" + age +", address='" + address + '\'' +'}';}public Emp(int id, String name, int gender, int age, String address) {this.id = id;this.name = name;this.gender = gender;this.age = age;this.address = address;}public int getId() {return id;}public void setId(int id) {this.id = id;}public String getName() {return name;}public void setName(String name) {this.name = name;}public int getGender() {return gender;}public void setGender(int gender) {this.gender = gender;}public int getAge() {return age;}public void setAge(int age) {this.age = age;}public String getAddress() {return address;}public void setAddress(String address) {this.address = address;}@Overridepublic boolean equals(Object o) {if (this == o) return true;if (o == null || getClass() != o.getClass()) return false;Emp emp = (Emp) o;return id == emp.id &&gender == emp.gender &&age == emp.age &&Objects.equals(name, emp.name) &&Objects.equals(address, emp.address);}@Overridepublic int hashCode() {return id; // 当前任务使用 id 作为 hashCode}
}相关文章:

四、查找算法
文章目录 一、查找算法介绍二、线性查找算法2.1 顺序查找2.2 二分查找(折半查找)2.3 插值查找2.4 斐波拉契(黄金分割法)查找算法 三、树表的查找3.1 二叉排序树3.1.1 引入3.1.2 基本介绍3.1.3 二叉树的遍历3.1.4 二叉树的删除 3.2…...

果蔬识别系统性能优化之路(三)
目录 前情提要遗留问题 解决方案优化查询速度优化ivf初始化的速度 下一步 前情提要 果蔬识别系统性能优化之路(二) 遗留问题 优化同步速度,目前大约30秒,不是一个生产速度 这次来解决遗留问题 通过console,发现两个…...

时序预测|基于小龙虾优化高斯过程GPR数据回归预测Matlab程序COA-GPR 多特征输入单输出 附赠基础GPR
时序预测|基于小龙虾优化高斯过程GPR数据回归预测Matlab程序COA-GPR 多特征输入单输出 附赠基础GPR 文章目录 一、基本原理二、实验结果三、核心代码四、代码获取五、总结 时序预测|基于小龙虾优化高斯过程GPR数据回归预测Matlab程序COA-GPR 多特征输入单输出 附赠基础GPR 一、…...

C#进阶-快速了解IOC控制反转及相关框架的使用
目录 一、了解IOC 1、概念 2、生命周期 二、IOC服务示例 1、定义服务接口 2、实现服务 三、扩展-CommunityToolkit.Mvvm工具包 Messenger信使 方式一(收发消息) 方式二(收发消息) 方式三(请求消息…...

C++内存布局
文章目录 C内存布局1.文字介绍2.图片介绍3.代码介绍 C内存布局 1.文字介绍 1.内核态空间 2.用户态空间 (1)栈区:存储局部变量和函数调用的相关信息,栈的特点是自动分配和释放,由操作系统管理。栈由高地址向低地址生长,通常为0x…...
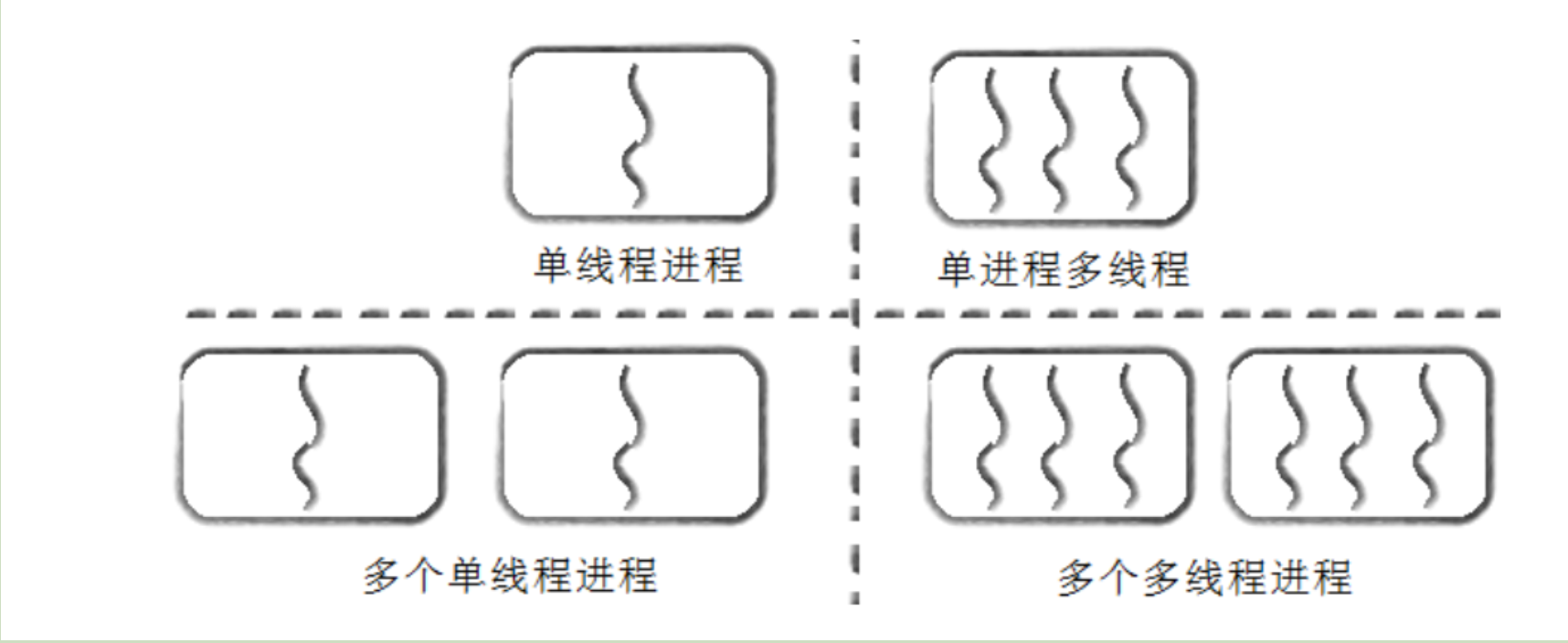
【Linux 19】线程概念
文章目录 🌈 一、线程的概念⭐ 1. 线程是什么⭐ 2. 线程的优点⭐ 3. 线程的缺点⭐ 4. 线程的异常⭐ 5. 线程的用途 🌈 二、进程和线程⭐ 1. 进程和线程的区别⭐ 2. 进程的多线程共享⭐ 3. 进程和线程的关系⭐ 3. 进程和线程的关系 🌈 一、线程…...

[区间dp]添加括号
题目描述 有一个 n n n 个元素的数组 a a a。不改变序列中每个元素在序列中的位置,把它们相加,并用括号记每次加法所得的和,称为中间和。现在要添上 n − 1 n - 1 n−1 对括号,加法运算依括号顺序进行,得到 n − …...

jenkins流水线+k8s部署springcloud微服务架构项目
文章目录 1.k8s安装2.jenkins安装3.k8s重要知识1.简介2.核心概念3.重要命令1.查看集群消息2.命名空间3.资源创建/更新4.资源查看5.描述某个资源的详细信息6.资源编辑7.资源删除8.资源重启9.查看资源日志10.资源标签 4.k8s控制台1.登录2.界面基本操作1.选择命名空间2.查看命名空…...
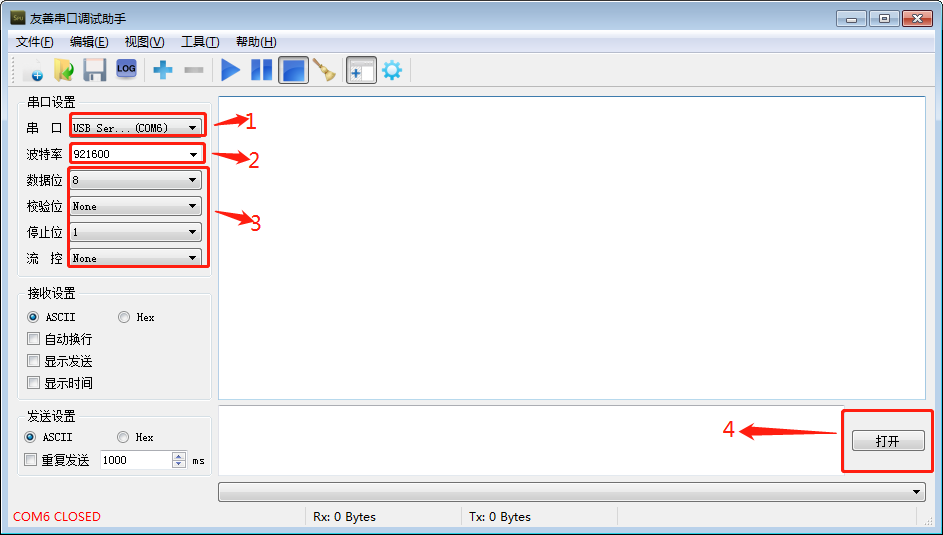
安卓开发板_联发科MTK开发评估套件串口调试
串口调试 如果正在进行lk(little kernel ) 或内核开发,USB 串口适配器( USB 转串口 TTL 适配器的简称)对于检查系统启动日志非常有用,特别是在没有图形桌面显示的情况下。 1.选购适配器 常用的许多 USB 转串口的适配器…...

vue+el-table 可输入表格使用上下键进行input框切换
使用上下键进行完工数量这一列的切换 <el-table :data"form.detailList" selection-change"handleChildSelection" ref"bChangeOrderChild" max-height"500"><!-- <el-table-column type"selection" width&quo…...

中国书法——孙溟㠭浅析碑帖《三希堂法帖》
孙溟㠭浅析碑帖《三希堂法帖》 全称是《三希堂石渠宝笈法帖》,是中国清代宫廷刻帖,一共三十二册。 清朝高宗弘历收藏了晋王羲之《快雪时晴帖》,王献之的《中秋帖》,王珣的《伯远帖》三种王氏原墨迹。故而把所藏法书之所…...
:颠覆传统的AI创作方式)
深入探讨生成对抗网络(GANs):颠覆传统的AI创作方式
在人工智能的快速发展中,生成对抗网络(Generative Adversarial Networks, GANs)无疑是一个引人注目的技术。自2014年由Ian Goodfellow等人首次提出以来,GANs已经在图像生成、文本生成、视频生成等多个领域展现出了惊人的能力。本文…...

vmware Vnet8虚拟网卡丢失的找回问题
vmware Vnet8虚拟网卡丢失的找回问题 1.打开VMware Workstation 2.然后点击Edit --> Virtual Network Edit --> 打开Virtual Network Edit框 , 3.点击最下面的的Restore Default 按钮, 3.恢复默认设置,这会在网络连接那块可以看到丢失…...

Python 从入门到实战13(字符串简介)
我们的目标是:通过这一套资料学习下来,通过熟练掌握python基础,然后结合经典实例、实践相结合,使我们完全掌握python,并做到独立完成项目开发的能力。 上篇文章我们通过举例学习了流程控制语句中的循环语句。今天继续讨…...

Redis_RDB持久化
基于RDB的持久化方式会把当前内存中所有的redis键值对数据以快照的方式写入硬盘文件中,如果需要恢复数据,就把快照文件读到内存中。 RDB快照文件是经压缩的二进制格式的文件,它的储存路径不仅可以在redis服务器启动前通过配置参数来设置&…...

SOP流程制定:vioovi ECRS工时分析软件的智慧引领
在现代制造业中,标准化操作流程(SOP)已成为提升生产效率、确保产品质量、降低运营成本的关键要素。SOP不仅为生产活动提供了明确的指导,还促进了企业管理的规范化和精细化。然而,如何科学、高效地制定SOP流程ÿ…...
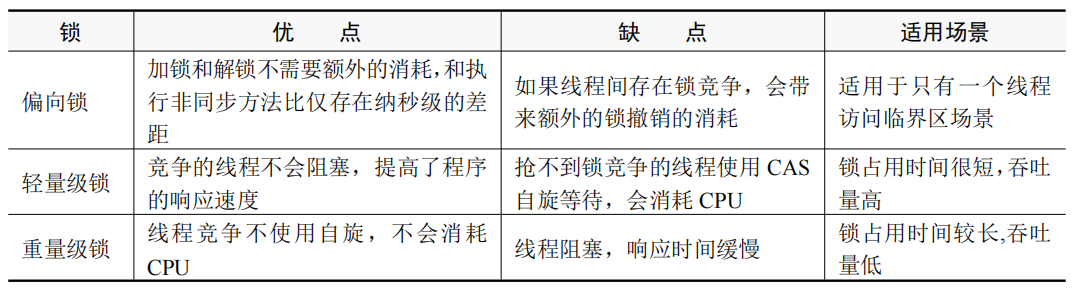
并发编程-synchronized解决原子性问题
并发编程-synchronized解决原子性问题 文章目录 并发编程-synchronized解决原子性问题零、说在前面一、线程安全问题1.1 什么是线程安全问题1.2 自增运算不是线程安全的1.3 临界区资源与临界区代码段 二、synchronized 关键字的使用2.1 synchronized 关键字作用2.2 synchronize…...

CSS之我不会
非常推荐html-css学习视频:尚硅谷html-css 一、选择器 作用:选择页面上的某一个后者某一类元素 基本选择器 1.标签选择器 格式:标签{} <h1>666</h1><style>h1{css语法} </style>2.类选择器 格式:.类…...

AI绘画:SD打光神器!(Stable Diffusion进阶篇:Imposing Consistent Light)
前言 在上一篇笔记中学习了如何简单地下载以及使用IC-Light,今天的内容会稍微有点不一样。 对于学过stable diffusion的小伙伴来说,forge UI和Comfy UI会更加熟悉一些。在IC-Light发布后,Openpose editor的开发者将其制作成了一个Forge UI上…...

QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期]
QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期] 第二期介绍:频道模块之频道管理 目录 QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期]第二期介绍:频道模块之频道管理获取用户详情获取用户频道列表获取频道详情获取子频道列表获…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
