9.11 codeforces Div 2
文章目录
- 9.11 Div 2
- A. Dora's Set(删除三个互质数)
- 思路
- 代码
- B. Index and Maximum Value(范围加减1求max)
- 思路
- 代码
- C. Dora and C++(加a/b,最小化极差)
- 思路
- 代码
9.11 Div 2
Dashboard - Codeforces Round 969 (Div. 2) - Codeforces
A. Dora’s Set(删除三个互质数)
集合s是l,r之间的数字
-
从集合 s 中选择三个不同的整数 a 、 b 和 c ,使得 gcd(a,b)=gcd(b,c)=gcd(a,c)=1 。
-
然后,从集合 ss 中删除这三个整数。
思路
由题意知,需要尽可能多的组成三个互质的数字。必然不能存在两个偶数,所以每个组合至少两个奇数。
由于集合s是连续序列,直接取相邻的三个数(两奇一偶),因而计算奇数个数,除以2就是答案。
代码
void solve()
{ int l,r;cin>>l>>r;int n=r-l+1;int j=n/2;if(n%2!=0) j=j+l%2;cout<<j/2<<'\n';
}
B. Index and Maximum Value(范围加减1求max)
对于一个整数数组,数字在 [ l , r ] [l,r] [l,r]范围内,进行+1或-1.每操作后,输出最大值。
审题不清,刚开始以为下标在某范围内,进行±,但平常也用不上算法,后来开始写ST,模板没记住,又废了好一会儿。
思路
看似复杂,实则只需考虑max,是否在范围内。
若不在范围内,顶多出现max-1变成了max ,最大值依旧为max
若在范围内,max++,便是答案
若不在范围内,max
在范围内,max—
代码
void solve()
{ int n,m,mx=0;char x;cin>>n>>m;fir(i,1,n){cin>>a[i];if(a[i]>mx)mx=a[i];}while(m--){int l,r;cin>>x>>l>>r;if(mx>=l&&mx<=r){ if(x=='+') mx++;else mx--;} cout<<mx<<' ';}cout<<'\n';
}
C. Dora and C++(加a/b,最小化极差)
一个数组可以选择对某个数字+a/b,进行无限次操作,得到最小极差
思路
我的整体思路没错,计算一个C,数组对C取模,将结果围成一个圈,两种转圈方法,取最小的。
两个细节有问题
-
c我简单的以为是min(a,b,|a-b|),实在太疏忽了。
比如(15,9),可以变成(15,18),此时他们的差值为3而不是6。这样太武断了,且没有说服力很强的论证,看起来就不像答案。
-
对于第二中转圈方法,我将小于C/2的 数字+C,最后用max-min
比如1 4 6 8 9,c=10
此时为(14-6=8),这样并不是最优的,(11-4=7才是)。之前遇到过相似题,当时按这个思路写对了,复杂。
问题应该这样解决:
- c=__gcd(a,b)
最终数组肯定是由多个a,b相加得到,可以表示为 c i = f a + f b + c i c_i=fa+fb+c_i ci=fa+fb+ci
即
c i = k c + b c_i=kc+b ci=kc+b
- w[i-1]+c-w[i]
这样将每一个i,作为开端,前面的数字作为末尾。遍历得出最小
最终答案有理有据,而我的武断猜想也很重要
代码
void solve()
{int n,a,b,ans;cin>>n>>a>>b;int c=__gcd(a,b);fir(i,1,n){cin>>w[i];w[i]%=c;}sort(w,w+n+1);ans=w[n]-w[1];//1fir(i,1,n){ans=min(ans,w[i-1]+c-w[i]);//2}cout<<ans<<'\n';
}
相关文章:

9.11 codeforces Div 2
文章目录 9.11 Div 2A. Doras Set(删除三个互质数)思路代码 B. Index and Maximum Value(范围加减1求max)思路代码 C. Dora and C(加a/b,最小化极差)思路代码 9.11 Div 2 Dashboard - Codeforces Round 969 (Div. 2) …...

二级菜单的两种思路(完成部分)
第一种 <el-form ref"formRef" :model"form" :rules"rules" label-width"120px"><el-form-item label"类型" prop"type"><el-select v-model"form.type" placeholder"请选择类型&q…...

【机器学习导引】ch2-模型评估与选择
文章目录 经验误差与过拟合 (Empirical error &overfitting)1. **均方误差(Mean Squared Error, MSE)**2. **均方根误差(Root Mean Squared Error, RMSE)**3. **平均绝对误差(Mean Absolute…...

二开ihoneyBakFileScan备份扫描
优点:可以扫描根据域名生成的扫描备份的扫描工具 二开部分:默认网址到字典(容易被封),二开字典到网址(类似test404备份扫描规则),同时把被封不能扫描的网址保存到waf_url.txt 中&am…...

leetcode21. 合并两个有序链表
思路: 用一个新链表来表示合并后的有序链表, 每次比较两个链表,将较小的那个结点存储至新链表中 # Definition for singly-linked list. # class ListNode(object): # def __init__(self, val0, nextNone): # self.val val # …...

搭建 WordPress 及常见问题与解决办法
浪浪云活动链接 :https://langlangy.cn/?i8afa52 文章目录 环境准备安装 LAMP 堆栈 (Linux, Apache, MySQL, PHP)配置 MySQL 数据库 安装 WordPress配置 WordPress常见问题及解决办法数据库连接错误白屏问题插件或主题冲突内存限制错误 本文旨在介绍如何在服务器上…...
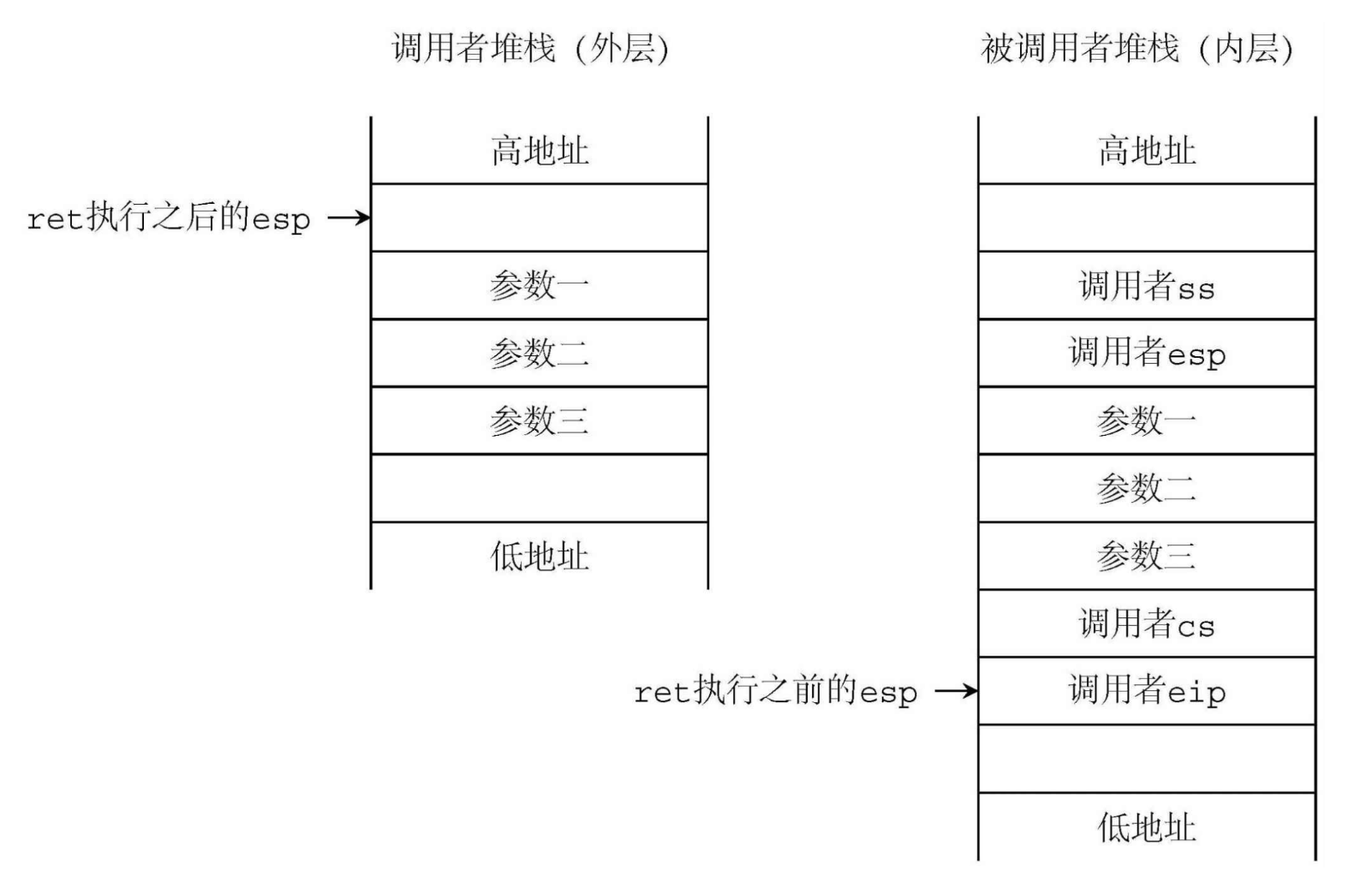
《ORANGE‘s 一个操作系统的实现》--保护模式进阶
保护模式进阶 大内存读写 GDT段 ;GDT [SECTION .gdt] ; 段基址, 段界限 , 属性 LABEL_GDT: Descriptor 0, 0, 0 ; 空描述符 LABEL_DESC_NORMAL: Descriptor 0, 0ffffh, DA_DRW ; Normal 描…...

【可变参模板】可变参类模板
可变参类模板也和可变参函数模板一样,允许模板定义含有0到多个(任意个)模板参数。可变参类模板参数包的展开方式有多种,以下介绍几种常见的方法。 一、递归继承展开 1.1类型模板参数包的展开 首先先看下面的代码: /…...

Linux 递归删除大量的文件
一般情况下 在 Ubuntu 中,递归删除大量文件和文件夹可以通过以下几种方式快速完成。常用的方法是使用 rm 命令,配合一些适当的选项来提高删除速度和效率。 1. 使用 rm 命令递归删除 最常见的方式是使用 rm 命令的递归选项 -r 来删除目录及其所有内容。…...

设计一个算法,找出由str1和str2所指向两个链表共同后缀的起始位置
假定采用带头结点的单链表保存单词,当两个单词有相同的后缀时,则可共享相同的后缀存储空间,例如,’loading’和’being’的存储映像如下图所示。 设str1和str2分别指向两个单词所在单链表的头结点,链表结点结构为 data…...

Python中如何判断一个变量是否为None
在Python中,判断一个变量是否为None是一个常见的需求,特别是在处理可选值、默认值或者是在函数返回结果可能不存在时。虽然这个操作本身相对简单,但围绕它的讨论可以扩展到Python的哲学、类型系统、以及如何在不同场景下优雅地处理None值。 …...

表观遗传系列1:DNA 甲基化以及组蛋白修饰
1. 表观遗传 表观遗传信息很多为化学修饰,包括 DNA 甲基化以及组蛋白修饰,即DNA或蛋白可以通过化学修饰添加附加信息。 DNA位于染色质(可视为微环境)中,并不是裸露的,因此DNA分子研究需要跟所处环境结合起…...

Android 跳转至各大应用商店应用详情页
测试通过机型品牌: 华为、小米、红米、OPPO、一加、Realme、VIVO、IQOO、荣耀、魅族、三星 import android.content.ActivityNotFoundException; import android.content.Context; import android.content.Intent; import android.content.pm.PackageInfo; import …...

Pywinauto鼠标操作指南
Pywinauto是一个强大的Python库,用于自动化Windows桌面应用程序的测试。它提供了一系列工具和API来模拟用户输入,包括键盘、鼠标事件,以及与各种窗口控件交互的能力。本文将详细介绍如何使用Pywinauto来执行鼠标操作,并通过一些示…...

VRAY云渲染动画怎么都是图片?
动画实际上是由一系列连续的静态图像(帧)组成的,当这些帧快速连续播放时,就形成了动画效果。每一帧都是一个单独的图片,需要单独渲染。 云渲染农场的工作方式: 1、用户将3D场景文件和动画设置上传到云渲染…...
)
共享内存(C语言)
目录 一、引言 二、共享内存概述 1.什么是共享内存 2.共享内存的优势 三、共享内存的实现 1.创建共享内存 2.关联共享内存 3.访问共享内存 4.解除共享内存关联 5.删除共享内存 四、共享内存应用实例 五、总结 本文将深入探讨C语言中的共享内存技术,介绍其原理、…...

《JavaEE进阶》----16.<Mybatis简介、操作步骤、相关配置>
本篇博客讲记录: 1.回顾MySQL的JDBC操作 2..Mybatis简介、Mybatis操作数据库的步骤 3.Mybatis 相关日志的配置(日志的配置、驼峰自动转换的配置) 前言 之前学习应用分层时我们知道Web应用程序一般分为三层,Controller、Service、D…...

HuggingFists算子能力扩展-PythonScript
HuggingFists作为一个低代码平台,很多朋友会关心如何扩展平台算子能力。扩展平台尚不支持的算子功能。本文就介绍一种通过脚本算子扩展算子能力的解决方案。 HuggingFists支持Python和Javascript两种脚语言的算子。两种语言的使用方式相同,使用者可以任选…...

WInform记录的添加和显示
1、程序 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Forms;namespace ComboBoxApp {public part…...

★ C++基础篇 ★ string类的实现
Ciallo~(∠・ω< )⌒☆ ~ 今天,我将继续和大家一起学习C基础篇第五章下篇----string类的模拟实现 ~ 上篇:★ C基础篇 ★ string类-CSDN博客 C基础篇专栏:★ C基础篇 ★_椎名澄嵐的博客-CSDN博客 目录 一 基础结构 二 迭代器 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
