智能优化算法-粒子群优化算法(PSO)(附源码)
目录
1.内容介绍
2.部分代码
3.实验结果
4.内容获取
1.内容介绍
粒子群优化算法 (Particle Swarm Optimization, PSO) 是一种基于群体智能的元启发式优化算法,由Kennedy和Eberhart于1995年提出。PSO模拟了鸟群或鱼群的觅食行为,通过粒子之间的相互作用来搜索最优解。
PSO的工作机制主要包括:
- 速度更新:每个粒子根据自身历史最佳位置和个人认知,以及群体历史最佳位置和社会认知来调整自己的飞行速度。
- 位置更新:粒子根据更新后的速度移动至新的位置,继续评估适应度值。
优点包括:
- 简单易用:算法概念简单,易于理解和实现。
- 快速收敛:通常能够在较少迭代次数内找到较好的解。
- 广泛应用:适用于多种优化问题,包括连续和离散优化。
不足之处:
- 可能的早熟收敛:在某些情况下,PSO可能会过早收敛到局部最优解。
- 参数敏感性:算法性能高度依赖于惯性权重等参数的选择。
- 缺乏多样性:后期搜索过程中可能导致种群多样性降低。
应用范围广泛,例如:
- 功能优化:解决单目标或多目标优化问题。
- 机器学习:用于特征选择、参数调优等。
- 工程设计:优化结构设计、电路设计等。
- 经济金融:投资组合优化、风险管理等。
总之,PSO作为一种成熟且有效的优化算法,在处理复杂优化问题方面有着显著的优势。随着进一步的研究和改进,PSO将继续在众多领域发挥作用。
2.部分代码
clc
clear
close all
%% 参数初始化
c1 = 1.5; % 学习因子
c2 = 1.5;
w=0.7; % 惯性权重
D=10; % 粒子维度
maxgen = 100; % 迭代次数
sizepop = 200; % 种群大小
Vmax = 0.5; % 速度的范围
Vmin = -0.5;
popmax = 5; % 搜索的范围
popmin = -5;
%% 种群初始化
for i = 1:sizepop
% 随机产生一个种群
pop(i,:) = rand(1,D)*10-5; % 初始化位置
V(i,:) = 0.5 * rands(1,D); % 初始化速度
% 适应度计算
fitness(i) = fit(pop(i,:));
end
%% 个体极值和群体极值
[bestfitness,bestindex] = max(fitness); % 默认将第一代的最大适应度值设置为最佳
zbest = pop(bestindex,:); % 全局最佳
gbest = pop; % 个体最佳
fitnessgbest = fitness; % 个体最佳适应度值
fitnesszbest = bestfitness; % 全局最佳适应度值
%% 迭代寻优
for i = 1:maxgen
for j = 1:sizepop
% 速度更新
V(j,:) = w*V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
% 速度越界检查
V(j,find(V(j,:)>Vmax)) = Vmax;
V(j,find(V(j,:)<Vmin)) = Vmin;
% 种群更新
pop(j,:) = pop(j,:) + V(j,:);
% 个体范围越界检查
pop(j,find(pop(j,:)>popmax)) = popmax;
pop(j,find(pop(j,:)<popmin)) = popmin;
% 适应度值计算
fitness(j) = fit(pop(j,:));
end
for j = 1:sizepop
% 个体最优更新
if fitness(j) < fitnessgbest(j)
gbest(j,:) = pop(j,:);
fitnessgbest(j) = fitness(j);
end
% 全局最优更新
if fitness(j) < fitnesszbest
zbest = pop(j,:);
fitnesszbest = fitness(j);
end
end
% 记录每一代的最优值
yy(i) = fitnesszbest;
end
%% 输出结果并绘图
[fitnesszbest zbest]
figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);
ylabel('适应度','fontsize',12);
legend('PSO')
3.实验结果

4.内容获取
粒子群优化算法matalb源代码:主页欢迎自取,点点关注,非常感谢!
相关文章:

智能优化算法-粒子群优化算法(PSO)(附源码)
目录 1.内容介绍 2.部分代码 3.实验结果 4.内容获取 1.内容介绍 粒子群优化算法 (Particle Swarm Optimization, PSO) 是一种基于群体智能的元启发式优化算法,由Kennedy和Eberhart于1995年提出。PSO模拟了鸟群或鱼群的觅食行为,通过粒子之间的相互作用…...

vue系统获取授权平台授权码实现单点登录、注销功能
公司平台需要对接别的平台 实现单点登录 注销。简而言之,不需要在自己公司系统登录 统一在别的平台登录后获取到登录凭证(授权码) 在本公司系统实现免密登录的功能。 流程: 跳转授权页面和保存授权码的代码: hrefLog…...

Java之枚举
目录 枚举 引入 定义 代码示例 常用方法 代码示例 枚举的优缺点 枚举和反射 面试题 枚举 引入 枚举是在JDK1.5以后引入的。主要用途是:将一组常量组织起来,在这之前表示一组常量通常使用定义常量的方式: publicstaticintfinalRED1;…...

八、适配器模式
适配器模式(Adapter Pattern)是一种结构型设计模式,它允许不兼容的接口之间进行合作。适配器模式通过创建一个适配器类来转换一个接口的接口,使得原本由于接口不兼容无法一起工作的类可以一起工作。 主要组成部分: 目标…...

关于E-R图
一 什么是E-R图 E-R图(Entity-Relationship Diagram)是一种数据建模工具,用于描述数据库中实体之间的关系。它使用实体(Entity)、属性(Attribute)和关系(Relationship&#…...

DVWA通关教程
Brute Force Low 先进行一下代码审计 <?php // 检查是否通过GET请求传递了Login参数(注意:这里应该是username或类似的,但代码逻辑有误) if( isset( $_GET[ Login ] ) ) { // 从GET请求中获取用户名 $user $_GET[ us…...

网络学习-eNSP配置VRRP
虚拟路由冗余协议(Virtual Router Redundancy Protocol,简称VRRP) VRRP广泛应用在边缘网络中,是一种路由冗余协议,它的设计目标是支持特定情况下IP数据流量失败转移不会引起混乱,允许主机使用单路由器,以及即使在实际…...

Kafka【九】如何实现数据的幂等性操作
为了解决Kafka传输数据时,所产生的数据重复和乱序问题,Kafka引入了幂等性操作,所谓的幂等性,就是Producer同样的一条数据,无论向Kafka发送多少次,kafka都只会存储一条。注意,这里的同样的一条数…...

JavaScript知识点1
目录 1.JavaScript中常用的数组方法有哪些? 2.JavaScript的同源策略? 3.JavaScript中的 NaN 是什么? 4.JavaScript中的split、slice、splice函数区别? 1.JavaScript中常用的数组方法有哪些? 在 JavaScript 中&…...

51单片机个人学习笔记11(AT24C02-I2C总线)
前言 本篇文章属于STC89C52单片机(以下简称单片机)的学习笔记,来源于B站教学视频。下面是这位up主的视频链接。本文为个人学习笔记,只能做参考,细节方面建议观看视频,肯定受益匪浅。 [1-1] 课程简介_哔哩…...

创建Java项目,可实现main方法运行,实现对性能数据的处理
1、Android Studio无法执行Java类的main方法问题及解决方法 Android Studio无法执行Java类的main方法问题及解决方法_delegatedbuild-CSDN博客 D:\workspaces\performanceTools\.idea 文件夹下,gardle.xml ,添加依赖 <option name"delegatedBuild"…...

JavaWeb(后端)
MVC MVC 就是 Model View Controller 的缩写,属于一种软件架构设计模式一种思想,把我们的项目分为控制器(Controller)、模型(Model)、视图(view)三个部分,model就是处理…...

828华为云征文 | 华为云Flexusx实例,高效部署Servas书签管理工具的优选平台
前言 华为云Flexus X实例,Servas书签管理工具部署的优选平台!828节日特惠,让高效管理您的知识宝藏触手可及。Flexus X实例以其卓越的算力、灵活的资源配置和智能调优技术,为Servas提供了稳定、高效的运行环境。无论是快速访问、安…...

分治法和动态规划法
一、分治法(Divide and Conquer) 定义 分治法是一种将大问题分解成若干个小问题,递归地解决这些小问题,然后将这些小问题的解合并起来得到原问题的解的算法策略。(子问题之间相互独立) 基本步骤 1.分解…...

【FreeRL】我的深度学习库构建思想
文章目录 前言参考python环境效果已复现结果 综述DQN.py(主要)算法实现参数修改细节实现显示训练,保存训练 Buffer.pyevaluate.pylearning_curves 前言 代码实现在:https://github.com/wild-firefox/FreeRL 欢迎star 参考 动手学强化学习e…...

Docker部署nginx容器无法访问80端口
问题说明 在阿里云ECS服务器上部署一台CentOS服务器,然后在里面安装了docker服务。用docker部署了nginx,开启docker中的nginx服务,映射宿主机端口80 把阿里云服务器上面的安全组放开了80端口 但是还是无法访问nginx的80web界面 问题分析 查…...

Python语言开发学习之使用Python预测天气
什么是wttr? 使用Python预测天气的第一步,我们要了解wttr是什么。wttr.in是一个面向控制台的天气预报服务,它支持各种信息表示方法,如面向终端的ANSI序列(用于控制台HTTP客户端(curl、httpie或wget))、HTML(用于web浏览器)或PNG(…...
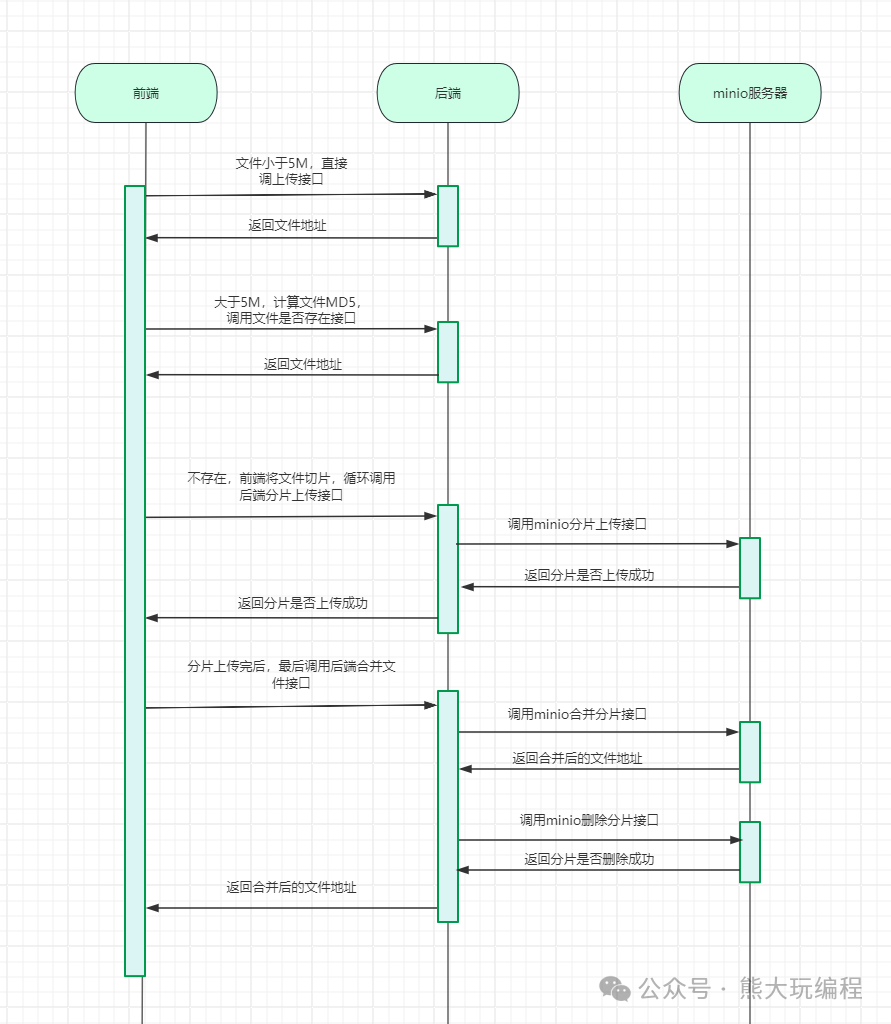
minio实现大文件断点续传
最近工作中遇到一个需求,用户需要上传大文件几百M,为了更好的用户体验,需要支持断点续传,秒传,上传进度条等功能。需求如下: 方案有两种: 第一种:前端直接将整个大文件丢到后端&…...

Qt绘制动态仪表(模仿汽车仪表指针、故障灯)
背景: 项目需要,可能需要做一些仪表显示。此篇除了介绍实现方法,还要说明心路历程。对我而言,重要的是心理,而不是技术。写下来也是自勉。 本人起初心里是比较抵触的,从业20多年了,深知所谓界…...
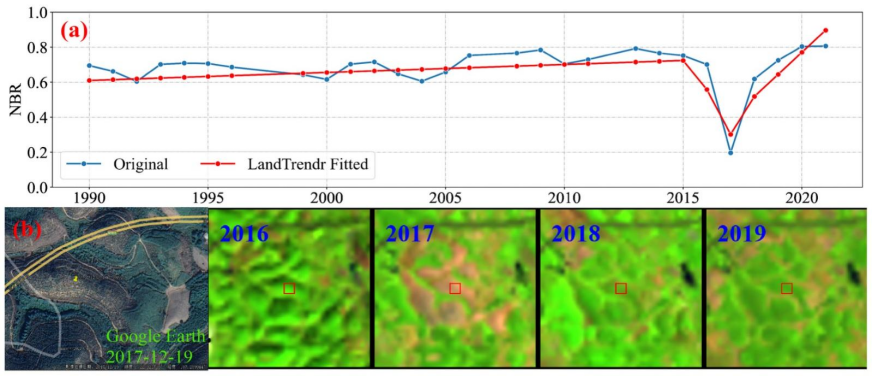
【视频教程】GEE遥感云大数据在林业中的应用与典型案例实践
近年来遥感技术得到了突飞猛进的发展,航天、航空、临近空间等多遥感平台不断增加,数据的空间、时间、光谱分辨率不断提高,数据量猛增,遥感数据已经越来越具有大数据特征。遥感大数据的出现为相关研究提供了前所未有的机遇…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
