字符串的KMP算法详解及C/C++代码实现
1. 原由
紧接上文,我们知道了暴力匹配的算法在时间运行上的缺陷,假设字符串T的长度为n,字符串P的长度为m,则整个算法的时间复杂度为O( n * m ),而对于一个复杂的现实情况而言 n >> m >> 2 (即n远远大于m,m远远大于常数),这样的计算计算机的负担很重。
请思考一个暴力匹配的情况:
给定一个主字符串
T = “AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB”(47位)
同时给定模式串 P = “AAAAAB”(6位)
试问搜索的情况,很显然,暴力搜索对于每一次搜索,都要搜索到最后一个字符才能进行下一轮的搜索,因此进行的计算近似可以理解为:O(47 * 6) ,对于这样很少的数据已经有很高的计算量了。
KMP算法一种改进的模式匹配算法,是D.E.Knuth、V.R.Pratt、J.H.Morris于1977年联合发表,KMP算法又称克努特-莫里斯-普拉特操作, KMP算法与前文的暴力匹配算法,核心的区别就是没有不匹配的回溯,而是根据整个字符串的情况进行一次位移,这样大大减少了回溯产生的缺陷,KMP算法的时间复杂度可以优化到 O( n + m)级别,是二次优化到线性的程度。
2.构造next表(以-1开头)
对于模式串P而言,我们需要知道模式串中P的每一位的前一位是否存在相等的完全相等的前后缀,并且求这个最大的完全相等的前后缀,如一个模式串”ABCABDE”对于第倒数第二位字符而言,其符合情况的前后缀就是”AB”,而最后一位则没有完全相等的前后缀。
PS:何为前后缀:如一个字符串”ABCD”,其前缀有可能为”A”“AB”“ABC”(即除去本身的全部字符),同理,则后缀可能为:”D””CD””BCD”
我们需要求的就是每一个字符其相对应的最大前后缀数,这样与模式串P一一对应的表称之为next表。
因此”ABCABDE”的next表为:-1 0 0 0 1 2 0 (字符用空格隔开)
那么我们该如何实现代码呢?
对于每一个当前需要判断的字符而言,在构造next表时,应该向前进行比对,以上一个已经判断的情况为基础(初始值赋-1,部分教程中初始值赋0,两者没有实质区别),后缀如果+1位置的字符与前缀+1位置的字符相等,则next[i]就是next[i-1]+1,而如果不相等,则说明无法匹配,则next[i]=0。
3. KMP实现
与暴力匹配极其相似,利用while循环的条件控制, 进行匹配失败时,只需要将失败的模式串P的索引指向next表中对应的数值即可,其余匹配照旧线性执行即可。
4. 实现代码(仅作参考)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;int *buildNext(char *P){int m = strlen(P) , j=0;int * N = new int[m];int t = N[0] = -1;while( j < m-1 ){if( 0 > t || P[j] == P[t] ){N[++j] = ++t;}else{t = N[t];}}return N;
}int KMP(char T[],char P[]){ //T--主串,P--模式串int *next = buildNext(P); //构造NEXT表int n = strlen(T) , i=0;int m = strlen(P) , j=0;while( j<m && i<n ){if( j<0 || T[i]==P[j] ){i++;j++;}else{j = next[j];}}delete []next;return i-j;
}int main(){char org[] = "ABABABABABD";char str[] = "ABABD";int ans = KMP(org,str);cout << ans <<endl;return 0;
}
输出6,即经过6位,在第七位发生匹配
相关文章:

字符串的KMP算法详解及C/C++代码实现
1. 原由 紧接上文,我们知道了暴力匹配的算法在时间运行上的缺陷,假设字符串T的长度为n,字符串P的长度为m,则整个算法的时间复杂度为O( n * m ),而对于一个复杂的现实情况而言 n >> m >> 2 (即…...

2024年数学建模比赛题目及解题代码
目录 一、引言 1. 1竞赛背景介绍 1.1.1数学建模竞赛概述 1.1.2生产过程决策问题在竞赛中的重要性 1.2 解题前准备 1.2.2 工具与资源准备 1.2.3 心态调整与策略规划 二、问题理解与分析 三、模型构建与求解 3.1 模型选择与设计 3.1.1 根据问题特性选择合适的数学模型类…...

BERT 论文逐段精读【论文精读】
BERT: 近 3 年 NLP 最火 CV: 大数据集上的训练好的 NN 模型,提升 CV 任务的性能 —— ImageNet 的 CNN 模型 NLP: BERT 简化了 NLP 任务的训练,提升了 NLP 任务的性能 BERT 如何站在巨人的肩膀上的?使用了哪些 NLP 已有的技术和思想ÿ…...
)
在Flask中实现跨域请求(CORS)
在Flask中实现跨域请求(CORS,Cross-Origin Resource Sharing)主要涉及到对Flask应用的配置,以允许来自不同源的请求访问服务器上的资源。以下是在Flask中实现CORS的详细步骤和方法: 一、理解CORS CORS是一种机制&…...
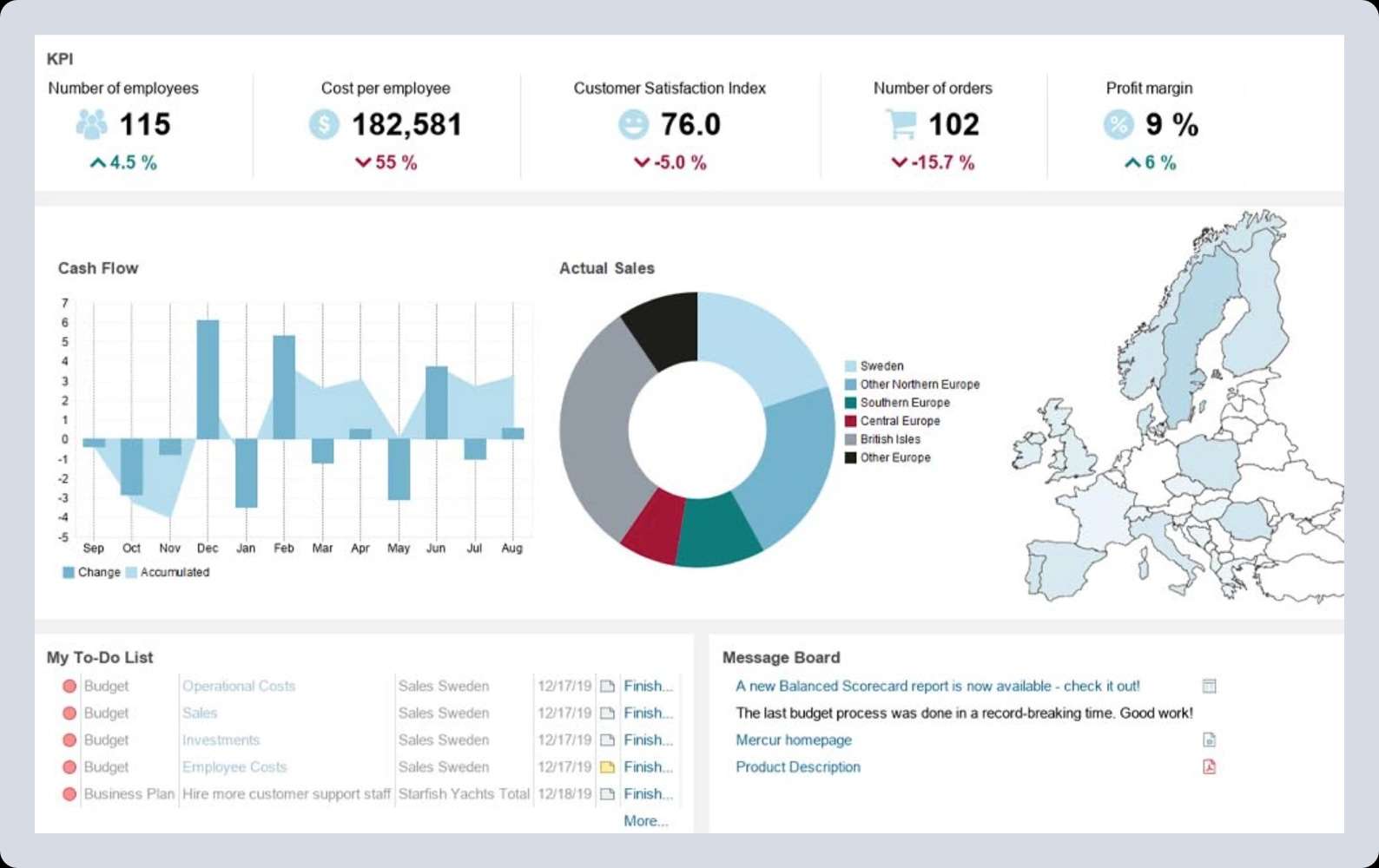
在桌面商业分析应用程序中启用高级 Web UI
挑战 Mercur Business Control 应用程序在企业界,尤其是金融领域,拥有悠久的应用历史。它帮助企业处理、可视化和分析海量数据,从而做出明智的商业决策。 随着产品的不断演进和现代化,Mercur Solutions AB 为该应用创建了 Web 客…...

CentOS Stream 8 通过 Packstack 安装开源 OpenStack(V版)
1、环境规划以及网卡配置 controller IP:192.168.235.101 compute IP:192.168.235.102 控制节点 [rootluck ~]# cd /etc/sysconfig/network-scripts/ [rootluck network-scripts]# vi ifcfg-ens160 [rootluck network-scripts]# cat ifcfg-ens160 TYP…...

OpenSSL工具验证RSA证书
openssl x509 是一个用于处理 X.509 证书的命令行工具。常用的 openssl x509 命令: -in <file>:指定输入文件。-out <file>:指定输出文件。-noout:不输出证书信息。-text:以文本格式输出证书信息。-pubke…...

架构师白话分布式系统
对于分布式系统的定义,大致可以理解为如下的两个点 分布式系统从整体的体量来说,它内部是由很多的服务器、服务实例组成。所提供的用户服务是由一组相互独立运行的服务器来提供。对于用户来说,这个多服务器的系统就跟一个服务器一样,感觉不到每个单独的服务器实例的存在。从…...

C++ 中 vector 的常用功能介绍
在 C 中,vector 是一种常用的动态数组容器,提供了方便的自动扩展、内存管理以及各种便捷的操作方法。它是 C 标准模板库(STL)的一部分,适用于需要动态存储和管理大量元素的场景。 在本文中,我们将简要介绍…...

[QT] QT事件与事件重写
一.事件 事件(event)是由系统或者 Qt本身在不同的场景下发出的。当用户按下鼠标、敲下键盘,或者是窗口关闭等都会发出一个相应的事件。 一些事件在用户操作时发出(如鼠标/键盘事件); 另一些事件则是由系统自动发出(如计时器事件)。 Qt窗口中对于产生的一系列事件都…...

c# 视觉识别图片文字 二维码
1.二维码识别 插件 ZXing.Net using System; using System.Drawing; // 如果你使用的是System.Drawing.Common using ZXing;class Program {static void Main(){string imagePath "path_to_your_qr_code_image.png";var barcodeBitmap (Bitmap)Image.FromFile(im…...

UEFI——访问PCI/PCIE设备(二)
一、支持访问PCI/PCIE设备的Protocol UEFI中提供了两个主要的模块来支持PCI总线,一是PCI Host Bridge(PCI主桥)控制器驱动,另一个是PCI总线驱动。这两个模块是和特定的平台硬件绑定的,在这种机制下,屏蔽了…...

决策树算法的介绍与应用
目录 引言 决策树算法的基本原理 表格总结:决策树的构建步骤 决策树算法的 MATLAB 实现 示例:使用决策树进行分类预测 决策树的应用场景 表格总结:决策树的主要应用领域 决策树的优势与局限 结论 引言 决策树是一种广泛应用于数据挖掘…...

杰发科技Bootloader(3)—— 基于7801的APP切到Boot
为了方便在APP中跳转到Boot重新进行升级,有两种办法,7840同样可以使用。 1. 调用reset接口进行复位,复位后会先进Boot,再自动跳转到App。 NVIC_SystemReset(); 2. 直接使用跳转指令,参考Boot跳转到App代码࿰…...

Leetcode面试经典150题-138.随机链表的复制
题目比较简单,重点是理解思想,random不管,copy一定要放在next 而且里面的遍历过程不能省略 解法都在代码里,不懂就留言或者私信 /* // Definition for a Node. class Node {int val;Node next;Node random;public Node(int val…...

freemarker模板学习笔记
文章目录 freemarker常用指令if-elseif-else指令switch, case, default, break指令list, else, items, sep, break 指令<#list>指令语法<#else> 指令<#items> 指令<#sep> 指令<#break> 指令 include 指令<#include> 基础知识<#include&…...

高亚科技与广东海悟携手,打造全流程电子竞标管理平台!
近日,中国企业管理软件资深服务商高亚科技与广东海悟科技有限公司(以下简称“海悟”)正式签署合作协议,双方将基于高亚科技的8Manage SRM系统,推进海悟采购管理的数字化升级,实现全流程在线电子竞标管理&am…...

240908-结合DBGPT与Ollama实现RAG本地知识检索增强
A. 最终效果 B. 背景说明 DBGPT在0.5.6版本中开始支持Ollama:v0.5.6 版本更新 网友对其Web端及界面端的设置进行了分享: feat(model): support ollama as an optional llm & embedding proxy by GITHUBear Pull Request #1475 eosphoros-ai/DB-G…...

AMD ThinkSystem服务器上的 Linux 和 C 状态设置 - Lenovo ThinkSystem
受影响的配置 该系统可以是以下任何Lenovo服务器: ThinkSystem 、SR645( ThinkSystem )ThinkSystem ,SR645 V3( ThinkSystem )ThinkSystem ,SR635 V3( ThinkSystem )Th…...

Redis过期删除和缓存淘汰
1. 过期删除 在 Redis 中,键的过期删除机制主要包括惰性删除(Lazy Deletion)和定期删除(Periodic Deletion)。这两种策略有各自的优缺点,Redis 最终会结合这两种方法来管理过期键。 1.1 惰性删除…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
