python 实现euler modified变形欧拉法算法
euler modified变形欧拉法算法介绍
Euler Modified(改进)变形欧拉法算法,也被称为欧拉修改法或修正欧拉法(Euler Modified Method),是一种用于数值求解微分方程的改进方法。这种方法在传统欧拉法的基础上进行了优化,以减少误差。
基本原理
欧拉法是一种通过逐步逼近来计算函数值的方法,但在某些情况下,传统的欧拉法可能会引入较大的误差。改进的欧拉法通过使用平均斜率来减小误差。其基本思想是:在每个步骤中,首先使用初始点的斜率来估计下一个点的值,然后使用这两个点的平均斜率来计算该点的函数值。这种方法能更好地逼近真实的函数曲线。
计算步骤
- 初始化:设定初始条件,包括初始点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),步长ℎ,以及微分方程的表达式 y ′ = f ( x , y ) y′=f(x,y) y′=f(x,y)。
- 预测步骤:使用欧拉法的公式 y p r e d = y n + h ⋅ f ( x n , y n ) y_{pred}=y_n+h⋅f(x_n,y_n) ypred=yn+h⋅f(xn,yn)来预测下一个点的𝑦值,其中 y n y_n yn是当前点的𝑦值,{𝑥_𝑛}是当前点的𝑥值。
- 斜率计算:使用预测得到的点 ( x n + 1 , y p r e d ) (x_{n+1},y_{pred}) (xn+1,ypred)和原始点 ( x n , y n ) (x_n,y_n) (xn,yn)来计算两个点的平均斜率 k a v g = f ( x n + 1 , y p r e d ) + f ( x n , y n ) 2 k_{avg}=\frac{f(x_{n+1},y_{pred})+f(x_n,y_n)}{2} kavg=2f(xn+1,ypred)+f(xn,yn)。
- 校正步骤:使用平均斜率来计算下一个点的𝑦值,即 y n + 1 = y n + h ⋅ k a v g y_{n+1}=y_n+h⋅k_{avg} yn+1=yn+h⋅kavg。
优点与缺点
优点:
改进的欧拉法比传统的欧拉法具有更高的精度,因为它使用了平均斜率来减少误差。
它的实现相对简单,计算速度也较快。
缺点:
尽管比传统的欧拉法更精确,但改进的欧拉法仍然是一种一阶方法,其精度可能不足以满足所有需求。对于需要更高精度的应用,可能需要使用更高级的数值方法,如龙格-库塔法(Runge-Kutta methods)。
注意事项
- 在使用改进的欧拉法时,需要仔细选择步长ℎ,因为步长的大小会直接影响算法的精度和稳定性。
- 改进的欧拉法适用于求解常微分方程的初值问题,但不适用于所有类型的微分方程。
总的来说,Euler Modified(改进)变形欧拉法算法是一种有效的数值求解微分方程的方法,它在保持计算简单性的同时,提高了传统欧拉法的精度。然而,对于需要更高精度的应用,可能需要考虑其他更高级的数值方法。
euler modified变形欧拉法算法python实现样例
Euler modified (改进)方法是一种数值解微分方程的方法,它在Euler方法的基础上进行了修正,以提高数值解的准确性。下面是使用Python实现Euler modified方法的示例代码:
import numpy as np
import matplotlib.pyplot as pltdef euler_modified(f, t0, tn, y0, h):n = int((tn - t0) / h)t = np.linspace(t0, tn, n+1)y = np.zeros(n+1)y[0] = y0for i in range(n):y_star = y[i] + h * f(t[i], y[i])y[i+1] = y[i] + h * (f(t[i], y[i]) + f(t[i+1], y_star)) / 2.0return t, y# 定义微分方程 dy/dt = f(t, y)
def f(t, y):return y * (1 - t)# 设置初始条件和步长
t0 = 0
tn = 1
y0 = 1
h = 0.1# 使用Euler modified方法求解微分方程
t, y = euler_modified(f, t0, tn, y0, h)# 绘制数值解的图像
plt.plot(t, y)
plt.xlabel('t')
plt.ylabel('y')
plt.title('Numerical Solution of dy/dt = y * (1 - t)')
plt.grid(True)
plt.show()
在代码中,首先定义了一个名为euler_modified的函数,它接受微分方程f、积分的起始时间t0、终止时间tn、初始条件y0和步长h作为输入,然后利用Euler modified方法求解微分方程,并返回时间和数值解的数组。
然后定义了一个简单的微分方程f(t, y) = y * (1 - t)作为示例。然后设置初始条件t0=0、tn=1、y0=1和步长h=0.1。最后调用euler_modified函数得到数值解,并使用matplotlib.pyplot绘制数值解的图像。
相关文章:

python 实现euler modified变形欧拉法算法
euler modified变形欧拉法算法介绍 Euler Modified(改进)变形欧拉法算法,也被称为欧拉修改法或修正欧拉法(Euler Modified Method),是一种用于数值求解微分方程的改进方法。这种方法在传统欧拉法的基础上进…...

strcpy 函数及其缺点
目录 一、概念 二、strcpy 函数有什么缺点 1. 缺乏边界检查 2. 容易引发未定义行为 3. 不适合动态和未知长度的字符串操作 4. 替代方案的可用性 5. 效率问题 一、概念 strcpy 是 C 语言中的一个标准库函数,用于将源字符串复制到目标字符串中。它定义在 <…...

区块链-P2P(八)
前言 P2P网络(Peer-to-Peer Network)是一种点对点的网络结构,它没有中心化的服务器或者管理者,所有节点都是平等的。在P2P网络中,每个节点都可以既是客户端也是服务端,这种网络结构的优点是去中心化、可扩展…...
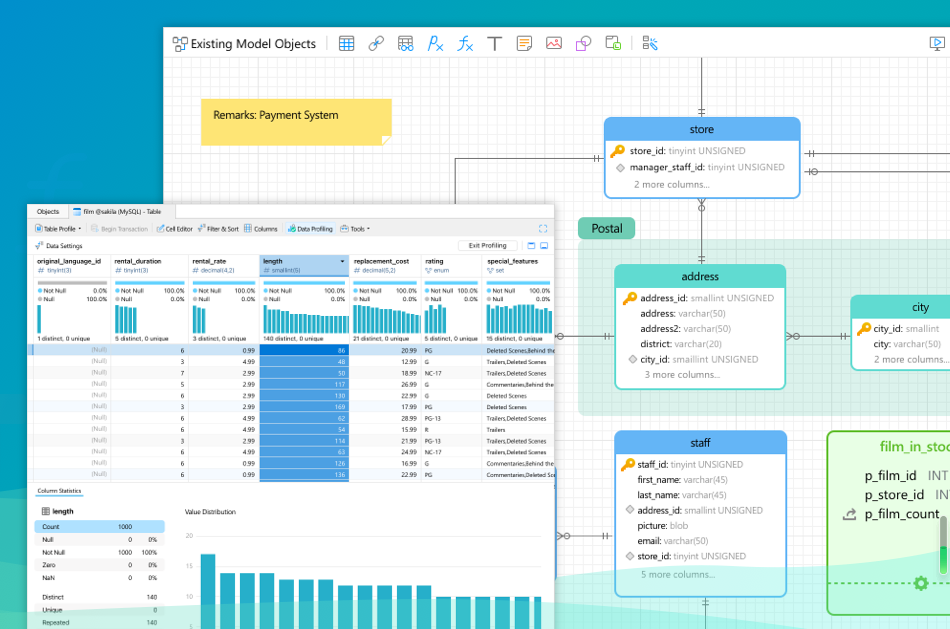
数据库管理的利器Navicat —— 全面测评与热门产品推荐
在数据库管理领域,Navicat无疑是一款深受欢迎的软件。作为一个强大的数据库管理和开发工具,它支持多种数据库类型,包括MySQL、MariaDB、MongoDB、SQL Server、Oracle、PostgreSQL等。本文将全面测评Navicat的核心功能,同时推荐几款…...

如何让Google收录我的网站?
其实仅仅只是收录,只要在GSC提交网址,等个两三天,一般就能收录,但收录是否会掉,这篇内容收录了是否有展现,排名,就是另外一个课题了,如果不收录,除了说明你的网站有问题&…...

03 Flask-添加配置信息
回顾之前学习的内容 02 Flask-快速上手 Flask 中最简单的web应用组成 1. 导入核心库 Flask from flask import Flask2. 实例化 web应用 注意:不要漏了 app Flask(__name__) 中的 __name__ 表示:是从当前的py文件实例化 app Flask(__name__)3. 创…...
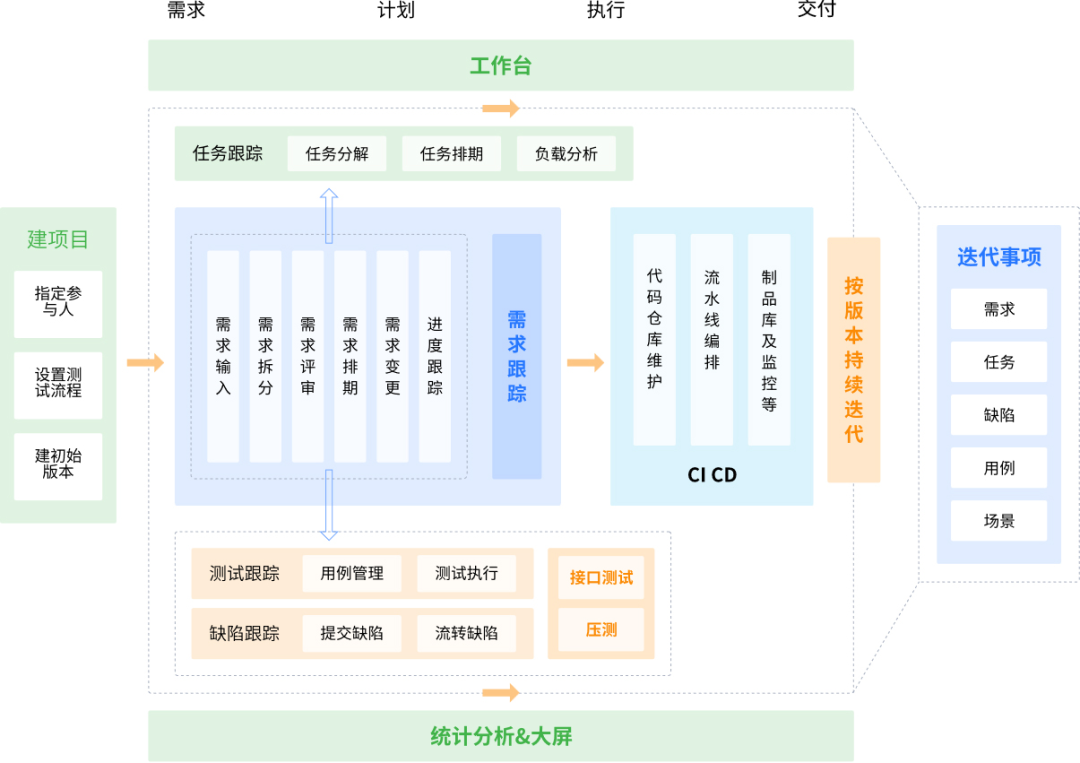
Codes 开源研发项目管理平台——敏捷测试管理创新解决方案
前言 Codes 是国内首款重新定义 SaaS 模式的开源项目管理平台,支持云端认证、本地部署、全部功能开放,并且对30人以下团队免费。它通过整合迭代、看板、度量和自动化等功能,简化测试协同工作,使敏捷测试更易于实施。并提供低成本的…...
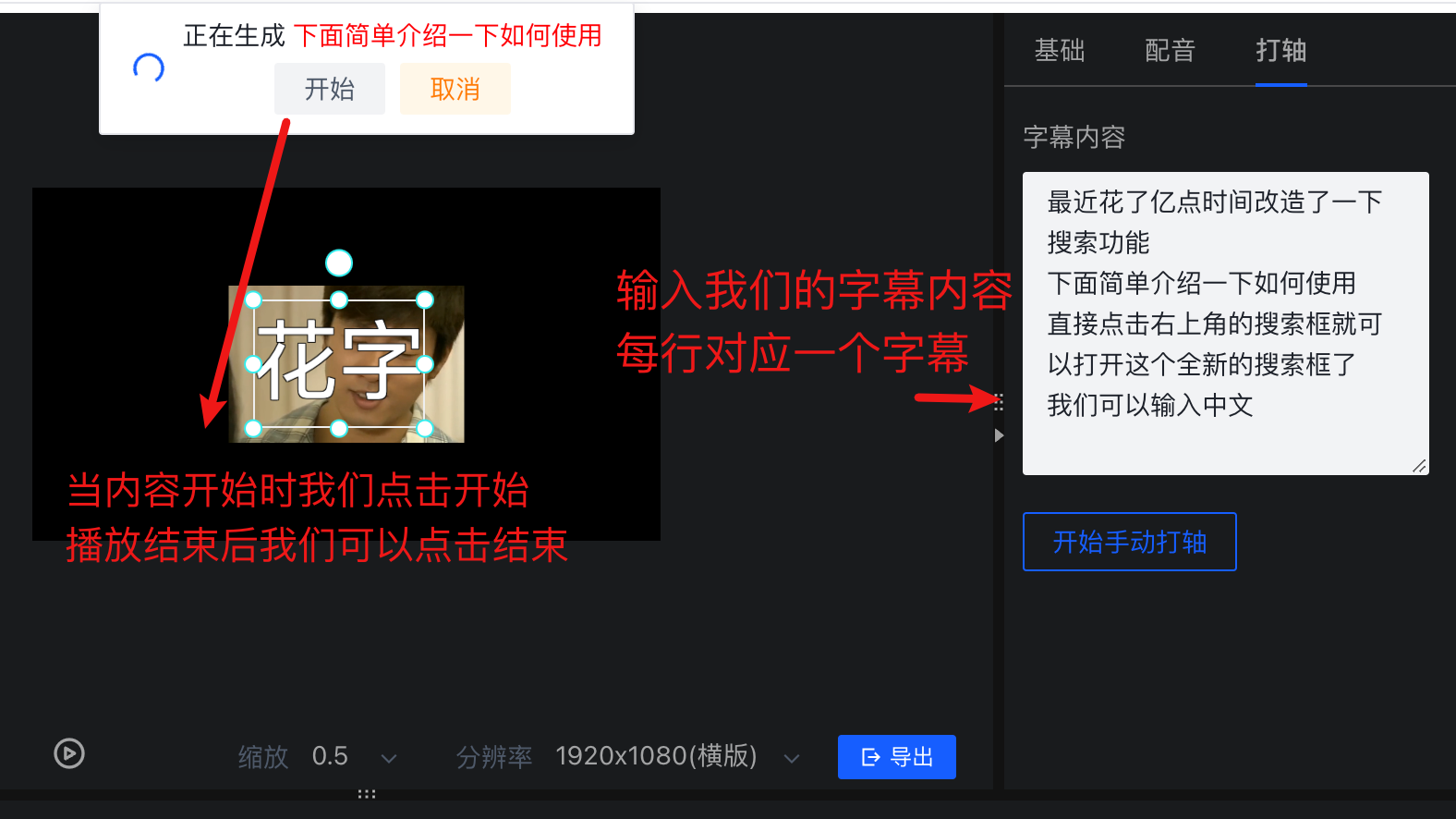
耗时一个月,我做了一个网页视频编辑器
最近又肝了一个多月,终于把这个网页视频编辑器做好了,下面我来简单介绍一下如何使用 注意目前该功能还处在测试阶段,可能会有很多问题,后续我会不断修复 体验地址 app.zyjj.cc 界面介绍 整个剪辑界面包括4个区,左边是…...

uniapp 做一个查看图片的组件,图片可缩放移动
因为是手机端,所以需要触摸可移动,双指放大缩小。 首先在components里建个组件 查看图片使用 uni-popup 弹窗 要注意 transform的translate和scale属性在同一标签上不会一起生效 移动就根据触摸效果进行偏移图片 缩放就根据双指距离的变大变小进行缩…...

卡车配置一键启动无钥匙进入手机控车
卡车智能一键启动无钥匙进入手机控车,通过手机应用程序与汽车内置硬件、软件的无线通信,实现对汽车的远程控制。 卡车改装一键启动的步骤包括安装门把手的感应装置、拆卸仪表台和门板,取出内部的待接线束,并将一键启动…...

计算机网络基础概念 交换机、路由器、网关、TBOX
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、VLAN是什么?二 、交换机三、路由器四、网关五、TBOX六、问题1 、网关和交换机的区别2、网关和路由器的区别 总结 前言 工作有感而发࿰…...

labview禁用8080端口
需求背景 最近电脑上安装了labview全家桶,发现idea的8080端口项目启动报错,一直提示8080端口被占用。最简单的办法就是找到8080端口的服务,然后关闭这个服务。但是我不想这么做,我想把labview的web服务器的端口给修改了。 操作教程 1、cmd查看8080端口 2、windows进程 同…...

字符串的KMP算法详解及C/C++代码实现
1. 原由 紧接上文,我们知道了暴力匹配的算法在时间运行上的缺陷,假设字符串T的长度为n,字符串P的长度为m,则整个算法的时间复杂度为O( n * m ),而对于一个复杂的现实情况而言 n >> m >> 2 (即…...

2024年数学建模比赛题目及解题代码
目录 一、引言 1. 1竞赛背景介绍 1.1.1数学建模竞赛概述 1.1.2生产过程决策问题在竞赛中的重要性 1.2 解题前准备 1.2.2 工具与资源准备 1.2.3 心态调整与策略规划 二、问题理解与分析 三、模型构建与求解 3.1 模型选择与设计 3.1.1 根据问题特性选择合适的数学模型类…...

BERT 论文逐段精读【论文精读】
BERT: 近 3 年 NLP 最火 CV: 大数据集上的训练好的 NN 模型,提升 CV 任务的性能 —— ImageNet 的 CNN 模型 NLP: BERT 简化了 NLP 任务的训练,提升了 NLP 任务的性能 BERT 如何站在巨人的肩膀上的?使用了哪些 NLP 已有的技术和思想ÿ…...
)
在Flask中实现跨域请求(CORS)
在Flask中实现跨域请求(CORS,Cross-Origin Resource Sharing)主要涉及到对Flask应用的配置,以允许来自不同源的请求访问服务器上的资源。以下是在Flask中实现CORS的详细步骤和方法: 一、理解CORS CORS是一种机制&…...
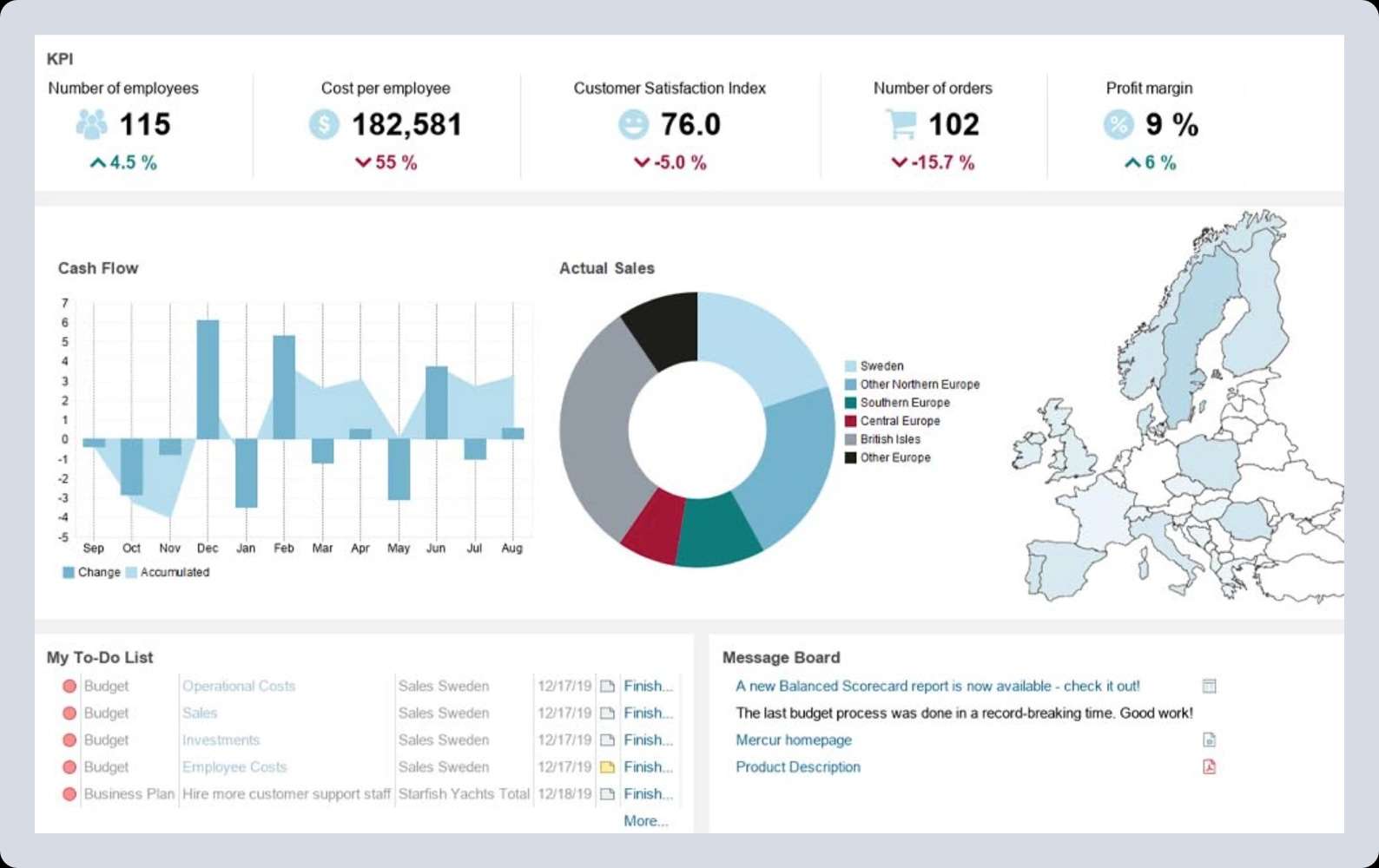
在桌面商业分析应用程序中启用高级 Web UI
挑战 Mercur Business Control 应用程序在企业界,尤其是金融领域,拥有悠久的应用历史。它帮助企业处理、可视化和分析海量数据,从而做出明智的商业决策。 随着产品的不断演进和现代化,Mercur Solutions AB 为该应用创建了 Web 客…...

CentOS Stream 8 通过 Packstack 安装开源 OpenStack(V版)
1、环境规划以及网卡配置 controller IP:192.168.235.101 compute IP:192.168.235.102 控制节点 [rootluck ~]# cd /etc/sysconfig/network-scripts/ [rootluck network-scripts]# vi ifcfg-ens160 [rootluck network-scripts]# cat ifcfg-ens160 TYP…...

OpenSSL工具验证RSA证书
openssl x509 是一个用于处理 X.509 证书的命令行工具。常用的 openssl x509 命令: -in <file>:指定输入文件。-out <file>:指定输出文件。-noout:不输出证书信息。-text:以文本格式输出证书信息。-pubke…...

架构师白话分布式系统
对于分布式系统的定义,大致可以理解为如下的两个点 分布式系统从整体的体量来说,它内部是由很多的服务器、服务实例组成。所提供的用户服务是由一组相互独立运行的服务器来提供。对于用户来说,这个多服务器的系统就跟一个服务器一样,感觉不到每个单独的服务器实例的存在。从…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
