OpenCV结构分析与形状描述符(12)椭圆拟合函数fitEllipseAMS()的使用
- 操作系统:ubuntu22.04
- OpenCV版本:OpenCV4.9
- IDE:Visual Studio Code
- 编程语言:C++11
算法描述
围绕一组2D点拟合一个椭圆。
该函数计算出一个椭圆,该椭圆拟合一组2D点。它返回一个内切于该椭圆的旋转矩形。使用了由[260]提出的近似均方差(AMS)方法。
对于椭圆,这个基集是 χ = ( x 2 , x y , y 2 , x , y , 1 ) \chi= \left(x^2, x y, y^2, x, y, 1\right) χ=(x2,xy,y2,x,y,1),这是一个包含六个自由系数的集合 A T = { A xx , A xy , A yy , A x , A y , A 0 } A^T=\left\{A_{\text{xx}},A_{\text{xy}},A_{\text{yy}},A_x,A_y,A_0\right\} AT={Axx,Axy,Ayy,Ax,Ay,A0}然而,要指定一个椭圆,只需要五个数字;主轴和次轴的长度 ( a , b ) (a,b) (a,b),位置 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)以及方向 θ。这是因为基集包含了直线、二次函数、抛物线和双曲线函数以及椭圆函数作为可能的拟合。如果发现拟合是一个抛物线或双曲线函数,则使用标准的 fitEllipse 方法。AMS 方法通过施加条件 A T ( D x T D x + D y T D y ) A = 1 A^T ( D_x^T D_x + D_y^T D_y) A = 1 AT(DxTDx+DyTDy)A=1 来限制拟合为抛物线、双曲线和椭圆曲线,其中矩阵 D x Dx Dx和 D y Dy DyDy 是设计矩阵D关于x 和y的偏导数。矩阵是通过逐行应用以下规则来形成的,针对点集中的每一个点: D ( i , : ) = { x i 2 , x i y i , y i 2 , x i , y i , 1 } D x ( i , : ) = { 2 x i , y i , 0 , 1 , 0 , 0 } D y ( i , : ) = { 0 , x i , 2 y i , 0 , 1 , 0 } \begin{align*} D(i,:)&=\left\{x_i^2, x_i y_i, y_i^2, x_i, y_i, 1\right\} & D_x(i,:)&=\left\{2 x_i,y_i,0,1,0,0\right\} & D_y(i,:)&=\left\{0,x_i,2 y_i,0,1,0\right\} \end{align*} D(i,:)={xi2,xiyi,yi2,xi,yi,1}Dx(i,:)={2xi,yi,0,1,0,0}Dy(i,:)={0,xi,2yi,0,1,0}
AMS 方法最小化成本函数:
ϵ 2 = A T D T D A A T ( D x T D x + D y T D y ) A T \begin{equation*} \epsilon ^2=\frac{ A^T D^T D A }{ A^T (D_x^T D_x + D_y^T D_y) A^T } \end{equation*} ϵ2=AT(DxTDx+DyTDy)ATATDTDA
通过求解广义特征值问题找到最小成本。
D T D A = λ ( D x T D x + D y T D y ) A \begin{equation*} D^T D A = \lambda \left( D_x^T D_x + D_y^T D_y\right) A \end{equation*} DTDA=λ(DxTDx+DyTDy)A
fitEllipseAMS 是 OpenCV 中用于拟合椭圆的一个函数,它使用了“代数方法”(Algebraic Method)来进行椭圆拟合。相比于 fitEllipse 函数使用的最小二乘法,fitEllipseAMS 更侧重于代数意义上的拟合,适用于某些特定的应用场景。
函数原型
RotatedRect cv::fitEllipseAMS
(InputArray points
) 参数
- points 输入的2D点集,存储在 std::vector<> 或 Mat 中。
代码示例
#include <iostream>
#include <opencv2/opencv.hpp>using namespace std;
using namespace cv;int main()
{// 创建一个空白图像Mat img( 400, 400, CV_8UC3, Scalar( 255, 255, 255 ) );// 创建一组2D点vector< Point2f > points;points.push_back( Point2f( 100, 100 ) );points.push_back( Point2f( 200, 100 ) );points.push_back( Point2f( 200, 200 ) );points.push_back( Point2f( 100, 200 ) );points.push_back( Point2f( 150, 150 ) );points.push_back( Point2f( 150, 250 ) );points.push_back( Point2f( 250, 150 ) );points.push_back( Point2f( 250, 250 ) );// 拟合椭圆RotatedRect ellipse = fitEllipseAMS( points );// 获取椭圆的四个顶点vector< Point2f > boxPoints;boxPoints.resize( 4 ); // 确保boxPoints至少有4个元素ellipse.points( boxPoints.data() );// 将 Point2f 转换为 Pointvector< Point > intBoxPoints;for ( const auto& pt : boxPoints ){intBoxPoints.push_back( Point( static_cast< int >( pt.x ), static_cast< int >( pt.y ) ) );}// 在原图上绘制椭圆polylines( img, intBoxPoints, true, Scalar( 0, 0, 255 ), 2, LINE_8 );// 绘制点集for ( const auto& pt : points ){circle( img, pt, 5, Scalar( 0, 255, 0 ), -1 );}// 显示结果imshow( "Ellipse Fitting (AMS)", img );waitKey( 0 );return 0;
}
运行结果

相关文章:

OpenCV结构分析与形状描述符(12)椭圆拟合函数fitEllipseAMS()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 围绕一组2D点拟合一个椭圆。 该函数计算出一个椭圆,该椭圆拟合一组2D点。它返回一个内切于该椭圆的旋转矩形。使用了由[260]提出的近…...

安卓显示驱动
安卓显示驱动是用于在Android设备上提供图形和视频显示的底层软件组件。 显示驱动在Android系统中扮演着至关重要的角色,它们负责将图形和视频内容从系统内存传输到显示屏上。这些驱动程序确保了用户界面、图像、视频和游戏等视觉元素的正常显示。以下是关于安卓显…...
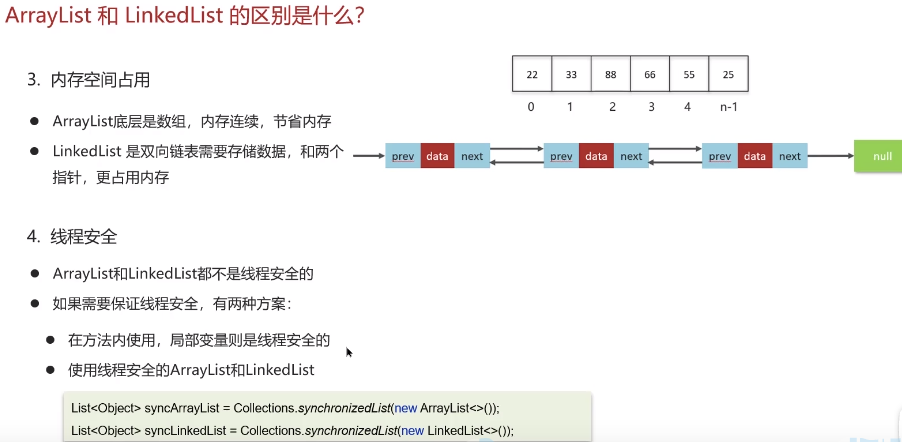
java重点学习-集合(List)
七 集合(List) 7.1 复杂度分析 7.2 数组 1.数组(Array)是一种用连续的内存空间存储相同数据类型 数据的线性数据结构。 2.数组下标为什么从0开始 寻址公式是:baseAddressi*dataTypeSize,计算下标的内存地址效率较高 3.查找的时间复杂度 随机(…...

【PCB测试】最常见的PCB测试方法
系列文章目录 1.元件基础 2.电路设计 3.PCB设计 4.元件焊接 5.板子调试 6.程序设计 7.算法学习 8.编写exe 9.检测标准 10.项目举例 11.职业规划 文章目录 一、PCB测试的好处1.发现错误2.降低成本3.节省时间4.减少退货率5.提高安全性 二、PCB测试内容1.孔壁质量2.电镀铜3.清…...
)
AtCoder Beginner Contest 370 ABCD题详细题解(C++,Python)
前言: 本文为AtCoder Beginner Contest 370 ABCD题的详细题解,包含C,Python语言描述,觉得有帮助或者写的不错可以点个赞 个人感觉D比C简单,C那里的字典序有点不理解, E应该是前缀和加dp,但是是dp不明白,等我明白了会更…...

斯坦福研究人员探讨大型语言模型在社交网络生成中的应用及其在政治同质性上的偏见
社交网络生成在许多领域有着广泛的应用,比如流行病建模、社交媒体模拟以及理解社交现象如两极化等。当由于隐私问题或其他限制无法直接观察真实网络时,创建逼真的社交网络就显得尤为重要。这些生成的网络对于在这些情况下准确建模互动和预测结果至关重要…...

一招教你找到Facebook广告的最佳发帖时间
在社交媒体上做广告时,时机是至关重要的。有时候你投放的广告参与度低,很有可能是因为你没有在适当的时机投放广告。这篇文章会教你如何找到适合自己的广告投放时间,如果你感兴趣的话,就继续看下去吧! 首先࿰…...

【数据库】MySQL-基础篇-多表查询
专栏文章索引:数据库 有问题可私聊:QQ:3375119339 目录 一、多表关系 1.一对多 2.多对多 3.一对一 二、多表查询概述 1.数据准备 2.概述 3.分类 三、内连接 1.隐式内连接 2.显式内连接 3.案例 四、外连接 1.左外连接 2.右外连…...

MongoDB事务机制
事务机制 1.事务概念 在对数据的操作的过程中,涉及到一连串的操作,这些操作如果失败,会导致我们的数据部分变化了,部分没变化。这个过程就好比如你去吃早餐,你点完餐了,并且吃完早餐了,没付钱你…...

大模型 LLM(Large Language Models)如今十分火爆,对于初入此领域的新人小白来说,应该如何入门 LLM 呢?是否有值得推荐的入门教程呢?
前言 很明显,这是一个偏学术方向的指南要求,所以我会把整个LLM应用的从数学到编程语言,从框架到常用模型的学习方法,给你捋一个通透。也可能是不爱学习的劝退文。 通常要达到熟练的进行LLM相关的学术研究与开发,至少…...

Python实现模糊逻辑算法
博客目录 引言 什么是模糊逻辑?模糊逻辑的应用场景模糊逻辑的基本思想 模糊逻辑的原理 模糊集合与隶属函数模糊推理系统(FIS)模糊规则和推理过程 Python实现模糊逻辑算法 面向对象的设计思路代码实现示例与解释 模糊逻辑算法应用实例&…...

MATLAB、FPGA、STM32中调用FFT计算频率、幅值及相位差
系列文章目录 文章目录 系列文章目录前言MATLABSTM32调用DSPSTM32中实现FFT关于初相位 FPGA 前言 最近在学习如何在STM32中调用FFT MATLAB 首先对FFT进行一下说明,我们输入N个点的数据到FFT中,FFT会返回N个点的数据,这些数据都是复数&#…...

基于SSM的医院药品库存系统的设计与实现---附源码76620
摘要 医院药品库存管理是医院管理的重要组成部分,对于保障医疗服务的质量和效率具有重要意义。传统的手工管理方式已经无法满足药品库存管理的需求,因此建立一个医院药品库存系统具有重要的实践价值。 使用Java语言开发医院药品库存系统可以兼容不同操作…...

Jupyter管理内核命令
1.显示有哪些内核 jupyter kernelspec list2.删除某个内核 jupyter kernelspec remove xxx3.添加某个内核 先激活环境 conda activate test_env然后安装ipykernel包 pip install ipykernel在虚拟环境中安装ipykernel包 python -m ipykernel install --name test_env安装过…...

简单分享-获取.txt文件内数据 文件内数据逗号分隔 分隔符 C语言
简单分享-获取.txt文件内数据 文件内数据逗号分隔 分隔符 C语言 数据存储到文件中,把文件数据读取到数组,方便数据处理。 # include <stdio.h> # include <stdlib.h> # include <string.h>#define DATANUM 307200 //数组个数 int ma…...

从0开始手把手带你入门Vue3
前言 本文并非标题党,而是实实在在的硬核文章,如果有想要学习Vue3的网友,可以大致的浏览一下本文,总体来说本篇博客涵盖了Vue3中绝大部分内容,包含常用的CompositionAPI(组合式API)、其它CompositionAPI以及一些新的特…...

C# USB通信技术(通过LibUsbDotNet库)
文章目录 1.下载LibusbDotNet库2.引入命名空间3. 实例化USB设备4.发送数据5.关闭连接 1.下载LibusbDotNet库 右击项目选择管理NuGet程序包在弹出的界面中搜索LibusbDotNet,然后下载安装。 2.引入命名空间 using LibUsbDotNet; using LibUsbDotNet.Main;3. 实例化…...

常用Java API
1 字符串处理 1.1 String 类 String 类是 Java 中不可变的字符序列。它提供了以下常用方法: length():返回字符串的长度。 charAt(index):返回指定索引处的字符。 substring(startIndex, endIndex):返回从 startIndex 到 endI…...

使用opencv优化图片(画面变清晰)
文章目录 需求影响照片清晰度的因素 实现降噪测试代码 锐化空间锐化Unsharp Masking频率域锐化对比测试 对比度增强常用算法对比测试 需求 对图像进行优化,使其看起来更清晰,同时保持尺寸不变,通常涉及到图像处理技术如锐化、降噪、对比度增强…...

Java 回顾方法的定义
一、方法的定义 1.修饰符(public static…)详见博客【Java 方法的定义】 2.返回值(int, double, char[],…., void)详见博客【Java 方法的定义】 3. break:跳出switch 结束循环,详…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...
