DFS算法专题(二)——穷举vs暴搜vs深搜vs回溯vs剪枝【OF决策树】
目录
1、决策树
2、算法实战应用【leetcode】
2.1 题一:全排列
2.2.1 算法原理
2.2.2 算法代码
2.2 题二:子集
2.2.1 算法原理【策略一】
2.2.2 算法代码【策略一】
2.2.3 算法原理【策略二,推荐】
2.2.4 算法代码【策略二,推荐】
2.3 题三:找出所有子集的异或总和再求和
2.3.1 算法原理
2.3.2 算法代码【解法一】(不推荐)
2.3.3 算法代码【解法二】(推荐)
2.4 题四:全排列 II
2.4.1 算法原理
2.4.2 算法代码
1、决策树
决策树是一种树形结构的监督学习算法,广泛应用于分类任务和回归任务中。它通过递归地将数据集分割成更小的子集,最终形成一个树形模型,用于预测新数据的输出。
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
决策树是一种十分常用的分类方法。它是一种监督学习,所谓监督学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。
面对上难度的DFS算法题,我们首先要做的就是画出决策树。
注意:画出的决策树越详细越好!!!

2、算法实战应用【leetcode】
2.1 题一:全排列
. - 力扣(LeetCode)
2.2.1 算法原理
- 画出决策树,记住:决策树越详细越好!!!
- 设置全局变量(全局变量的设置因题而异),本题设置二维数组ret为返回值,记录全部的全排列;数组path记录路径;布尔类型的check数组实现剪枝操作
- 对于递归函数,我们仍然要站在宏观角度,聚焦于某一层要做的事来设计
- DFS算法,不可避免的就是回溯、剪枝与函数出口等细节问题的考虑
- 对于本题回溯的设计,在dfs完下一层,回到当前层后,再进行恢复现场的操作(删除下一层在path中的数据),注意:本题需要对path和check均进行回溯操作
- 对于本题剪枝的设计,通过布尔数组的判断,判断数组中数据可否放进路径path中
- 对于本题递归函数的出口,将path中存放数据的数量和nums数组长度相比较,若相等,则添加到ret中。

2.2.2 算法代码
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;public List<List<Integer>> permute(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];dfs(nums);return ret;}public void dfs(int[] nums) {//函数出口if(path.size() == nums.length) {ret.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++) {if(!check[i]) {path.add(nums[i]);check[i] = true;dfs(nums);//将下一层中的相关数据删除 -> 回溯 -> 恢复现场 -> 1.path 2.check//add新数据时,递归仍然在本层中,add的是本层i位置处的新数据,//dfs完后,i仍然为本层add时的数据的下标,//此时回溯要将path和check恢复现场path.remove(path.size() - 1);check[i] = false;}}}
}2.2 题二:子集
. - 力扣(LeetCode)
2.2.1 算法原理【策略一】
- 画决策树
- 设置全局变量 : ①:List<List<Integer>> ret;//返回值 ②:List<Integer> path;//记录路径
- 设计函数头:void dfs(nums, pos);//pos为下一次进入path中元素的下标
- 设计函数体:①:选:path += nums[pos]; dfs(nums,pos+1);②:不选:dfs(nums,pos+1);
- 考虑函数出口:pos == nums.length;将path添加进ret中,return;
- 处理细节问题:①:回溯 -> 恢复现场:path.remove(pathsize()-1); ②:剪枝:无
2.2.2 算法代码【策略一】
class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums, 0);return ret;}public void dfs(int[] nums, int pos) {//函数出口if(pos == nums.length) {ret.add(new ArrayList<>(path));return;}//选path.add(nums[pos]);dfs(nums, pos + 1);//回溯 -> 恢复现场path.remove(path.size() - 1);//不选(不做任何操作即可)dfs(nums, pos + 1);}
}2.2.3 算法原理【策略二,推荐】
思想
- 分三个支线,每个节点就是一个子集,所以每刚进入递归函数时,就把path添加进ret中,pos依然为下一个要添加进path中的元素的下标。叶子节点即为函数出口。
步骤:
- 画决策树
- 设计代码 ①全局变量 ret/path ②函数头 void dfs(nums, pos); ③函数体 1.ret.add(path);2.依次枚举该节点后的元素 ④函数出口 无
- 细节问题 ①回溯 -> 恢复现场:path.remove(path,size()-1) ②剪枝 -> 无

2.2.4 算法代码【策略二,推荐】
class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums, 0);return ret;}public void dfs(int[] nums, int pos) {ret.add(new ArrayList<>(path));//从pos位置开始向后枚举for(int i = pos; i < nums.length; i++) {//依次枚举,下标为ipath.add(nums[i]);//从当前元素后面的元素中选dfs(nums, i + 1);//回溯 -> 恢复现场path.remove(path.size() - 1);}}
}2.3 题三:找出所有子集的异或总和再求和
. - 力扣(LeetCode)
2.3.1 算法原理
本题与上一题解题思想如出一辙,
解法一:直接cv上一题的代码,再将每组子集相异或再求和。(不推荐)
解法二:将path设置为每个子集的异或值(策越二,每个节点都是一个子集),再创建一个全局变量sum求和即可,回溯时直接利用异或消消乐的特性恢复现场即可。
解法二的时间效率更加优秀,建议大家使用解法二解题。
2.3.2 算法代码【解法一】(不推荐)
class Solution {List<List<Integer>> total;List<Integer> path;public int subsetXORSum(int[] nums) {total = new ArrayList<>();path = new ArrayList<>();List<Integer> sum = new ArrayList<>();dfs(nums, 0);for(int i = 0; i < total.size(); i++) {int ret = 0;for(int j = 0; j < total.get(i).size(); j++) {ret ^= (total.get(i).isEmpty() ? 0 : total.get(i).get(j));}sum.add(ret);}int val = 0;for(int x : sum) val += x;return val;}public void dfs(int[] nums, int pos) {total.add(new ArrayList<>(path));for(int i = pos; i < nums.length; i++) {path.add(nums[i]);dfs(nums, i + 1);path.remove(path.size() - 1);}}
}2.3.3 算法代码【解法二】(推荐)
class Solution {int path;//每个子集所有元素的异或值int sum;public int subsetXORSum(int[] nums) {path = 0;sum = 0;dfs(nums, 0);return sum;}public void dfs(int[] nums, int pos) {sum += path;for(int i = pos; i < nums.length; i++) {path ^= nums[i];dfs(nums, i + 1);//回溯 -> 恢复现场 -> 异或:消消乐path ^= nums[i];}}
}2.4 题四:全排列 II
. - 力扣(LeetCode)
2.4.1 算法原理
本题整体框架与上文题一全排列相同,回溯函数出口函数体等设计这里不再赘述。
由于出现重复的元素,故本题算法需要添加更多的剪枝操作。
在数组有序的情况下(有序时相同的元素才会相邻),我们可以这样来设计剪枝:
- 剪枝:
①:同一个元素只能出现一次 --> boolean[] check
②:在一个节点的分支中,相同数值的元素只能选择一次
- 筛选节点:
符合条件的节点:
check[i]==flase && (i==0 || nums[i-1] != nums[i] || check[i-1]==true)

2.4.2 算法代码
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;//同一个数据,只能出现一次public List<List<Integer>> permuteUnique(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];//数据有序的情况下,保证重复的元素是相邻的Arrays.sort(nums);dfs(nums);return ret;}public void dfs(int[] nums) {if(path.size() == nums.length) {ret.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++) {//剪枝 -> 筛选出符合条件的分支//同一个数据只能出现一次 && 一个节点上,相同数值的元素只能选择一次if(!check[i] && (i == 0 || nums[i - 1] != nums[i] || check[i - 1])) {path.add(nums[i]);check[i] = true;dfs(nums);//回溯 -> 恢复现场path.remove(path.size() - 1);check[i] = false;}}}
}END
相关文章:

DFS算法专题(二)——穷举vs暴搜vs深搜vs回溯vs剪枝【OF决策树】
目录 1、决策树 2、算法实战应用【leetcode】 2.1 题一:全排列 2.2.1 算法原理 2.2.2 算法代码 2.2 题二:子集 2.2.1 算法原理【策略一】 2.2.2 算法代码【策略一】 2.2.3 算法原理【策略二,推荐】 2.2.4 算法代码【策略二&#x…...

Spring Security 快速开始
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifactId></dependency> 一、认证 1、从数据中读数据完成认证 Service public class MyUserDetailsService implements UserDeta…...

Lua5.3 参考手册
《Lua 5.3 参考手册》是对 Lua 5.3 版本语言的官方定义。这份手册详细描述了 Lua 语言的语法、语义以及标准库和 C API。它是由巴西里约热内卢 Pontifical Catholic 大学的 PUC-Rio 团队开发的,并且是一个自由软件,广泛应用于世界各地的产品和项目中【9†…...

Centos如何配置阿里云的yum仓库作为yum源?
背景 Centos在国内访问官方yum源慢,可以用国内的yum源,本文以阿里云yum源为例说明。 快速命令 sudo mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.a…...

力扣139-单词拆分(Java详细题解)
题目链接:139. 单词拆分 - 力扣(LeetCode) 前情提要: 因为本人最近都来刷dp类的题目所以该题就默认用dp方法来做。 最近刚学完背包,所以现在的题解都是以背包问题为基础再来写的。 如果大家不懂背包问题的话&#…...

CSS —— display属性
用于指定一个元素在页面中的显示方式 HTML中标签元素大体被分为三种类型:块元素、行内元素和行内块元素 块元素 :block 1.独占一行 2.水平方向,占满它父元素的可用空间(宽度是父级的100%) 3.垂直方向,占据的…...

BTC ETF资金流入暴涨400%,市场下一步将如何发展?
近期,BTC现货ETF(交易所交易基金)市场出现了显著的资金流入,尤其是在9月10日,BTC ETF吸引了近1.17亿美元的资金流入,相较于前一天的3729万美元,暴涨了400%。这种现象引发了市场广泛关注…...
视频监控管理平台LntonAIServer视频智能分析抖动检测算法应用场景
在视频监控系统中,视频画面的稳定性对于确保监控效果至关重要。抖动现象是指视频画面中存在不稳定或频繁晃动的情况,这可能会影响视频的清晰度和可读性。LntonAIServer通过引入抖动检测功能,帮助用户及时发现并解决视频流中的抖动问题&#x…...

初识php库管理工具composer的体验【爽】使用phpword模板功能替换里面的字符串文本
需求: 做了一个租赁的项目,里面要求签署个人授权协议,里面要填写姓名,手机号,身份证号,签署日期等参数,格式如下图 格式: 如上图,word中的字符串模板变量使用${varname…...

每日一问:C++ 如何实现继承、封装和多态
每日一问:C 如何实现继承、封装和多态 C 是一门面向对象编程语言,通过继承、封装和多态这三个核心特性实现了对复杂系统的高效管理和扩展。继承让代码重用性得以提升,封装保护数据的完整性,而多态通过不同的接口实现了灵活性。本文…...

STM32常用数据采集滤波算法
例如,STM32进行滤波处理时,主要目的是处理数据采集过程中可能产生的噪声和尖刺信号。这些噪声可能来自电源干扰、传感器自身的不稳定性或其他外部因素。 1.一阶互补滤波 方法:取a0~1,本次滤波结果(1-a)本次采样值a上…...
9/12)
二分系列(二分查找)9/12
一、分情况讨论 1.左闭右闭:[left,right] 因为是左闭右闭,所以left和right都能直接取到。 #这里将>放到一起,当nums[mid]>target的时候, 要更新右边界,rightmid-1,这样就把一些相同的情况也切出去了 可以理解为找的第一个…...

如何通过可视化大屏,助力智慧城市的“城市微脑”建设?
在智慧城市的宏伟蓝图中,常常面临着一个关键挑战:如何确保这些理念和技术能够真正地惠及城市的每一个角落,每一个产业,以及每一位市民。问题的核心在于城市的具体应用场景,无论是横向的社区、园区、镇街、学校、酒店、…...

何时空仓库
某仓库现存货物 s 箱,每天上午出货 m 箱、下午进货 n 箱,若s≥m>n≥0,则第 k 天将会出现空仓的情况。请你帮仓库管理员编写程序,输入s、m 和 n,计算并输出 k。 输入格式 s,m,n (s≥m>n≥0) 输出格式 k 输入样例…...

美创获评CNVD年度原创漏洞发现贡献单位!
9月10日,第21届中国网络安全年会暨网络安全协同治理分论坛在广州成功举办。会上,美创科技首次获评“CNVD年度原创漏洞发现贡献单位”。 美创科技依托第59号安全实验室,专注数据安全技术和攻防研究。凭借深厚的技术积累与优势,被遴…...

Spring 循环依赖原理及解决方案
一、什么是循环依赖 循环依赖指的是一个实例或多个实例存在相互依赖的关系(类之间循环嵌套引用)。 举例: Component public class AService {// A中注入了BAutowiredprivate BService bService; }Component public class BService {// B中也…...
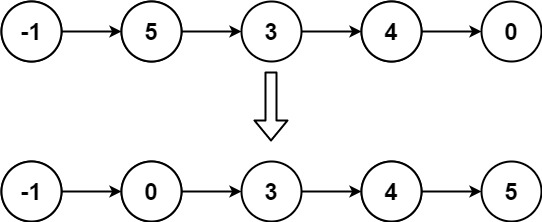
【数据结构与算法 | 灵神题单 | 插入链表篇】力扣2807, LCR 029, 147
1. 力扣2807:在链表中插入最大公约数 1.1 题目: 你一个链表的头 head ,每个结点包含一个整数值。 在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。 请你返回插入之后的链表。 两个…...

瑞芯微rv1126 Linux 系统,修改系统时区,包有效方法
在 Linux 系统中,修改时区的步骤通常包括创建符号链接到正确的时区文件,并确保相关的配置文件已正确更新。然而,某些系统可能有额外的步骤或需要修改其他配置文件来使更改生效。以下是一些步骤。 1. 创建符号链接 ln -sf /usr/share/zoneinfo/Asia/Hong_Kong /etc/localti…...

系统架构设计师:数据库设计
简简单单 Online zuozuo: 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo : 文章目录 系统架构设计师:数据库设计前言数据库基础概念数据模型三要素数据库的三级模型和两级…...

代码随想录刷题day31丨56. 合并区间,738.单调递增的数字,总结
代码随想录刷题day31丨56. 合并区间,738.单调递增的数字,总结 1.题目 1.1合并区间 题目链接:56. 合并区间 - 力扣(LeetCode) 视频讲解:贪心算法,合并区间有细节!LeetCode&#x…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

