力扣: 四数相加II
文章目录
- 需求
- 代码
- 结尾

需求
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < n
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
- (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
- (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例 2:
输入:nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出:1
提示:
n == nums1.length
n == nums2.length
n == nums3.length
n == nums4.length
1 <= n <= 200
-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228
代码
思路挺简单的, 就是遍历前两个数组, 将其能加起来的和的情况保存在map里, key是和, value是出现的次数, 然后再维护一个count来记录返回值, 再遍历后两个数组, 将其相加的和的负数去map里找, 有的话将 count 加上其value.
代码:
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {int length = nums1.length;Map<Integer, Integer> map = new HashMap<>(length * length);for (int i = 0; i < length; i++) {for (int j = 0; j < length; j++) {int n = nums1[i] + nums2[j];map.put(n, map.getOrDefault(n, 0) + 1);}}int count = 0;for (int i = 0; i < length; i++) {for (int j = 0; j < length; j++) {int n = nums3[i] + nums4[j];if( map.containsKey(-n) ){count += map.get(-n);}}}return count;
}
代码解释
初始化:
int length = nums1.length;
Map<Integer, Integer> map = new HashMap<>(length * length);
获取数组的长度(假设所有数组长度相等)。
创建一个 HashMap 用于存储 nums1 和 nums2 元素之和的出现频次。length * length 是一个初始容量估计,理论上足够容纳所有可能的和。
填充 HashMap:
for (int i = 0; i < length; i++) {for (int j = 0; j < length; j++) {int n = nums1[i] + nums2[j];map.put(n, map.getOrDefault(n, 0) + 1);}
}
使用两层嵌套循环遍历 nums1 和 nums2 的所有组合,计算它们的和,并将和及其出现的次数存入 map 中。
计算四元组数量:
int count = 0;
for (int i = 0; i < length; i++) {for (int j = 0; j < length; j++) {int n = nums3[i] + nums4[j];if (map.containsKey(-n)) {count += map.get(-n);}}
}
通过两层嵌套循环遍历 nums3 和 nums4 的所有组合,计算它们的和。
对于每个和 n,检查 map 是否包含 -n。如果包含,则将 map 中 -n 的计数值加到 count 中。
为什么是 -n?因为我们需要找到 a + b + c + d = 0 的情况,即 a + b = - (c + d)。所以对于 c + d 的和,我们需要在 map 中查找与之相反的值。
返回结果:
return count;
返回符合条件的四元组的数量。
执行结果:

结尾
以上 是我对这道算法的一些遐想和延伸, 可能不是最优解, 但是算法的优化嘛 本身就是一个思索的过程, 能在这个思索和迭代的过程中有所收获和乐趣就是在成长了, 欢迎大家一起来交流更多的解答…
相关文章:

力扣: 四数相加II
文章目录 需求代码结尾 需求 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < n nums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1: 输入…...

径向基函数神经网络RBFNN案例实操
简介 (来自ChatGPT的介绍,如有更正建议请指出) 径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)是一种特殊的前馈神经网络,其结构和特点与其他常见的神经网络有所不同,主要表现在以下几个方面: 网络结构三层结构:RBF神经网络通常由三层组成:输入层…...

Java-数据结构-二叉树-习题(一) (✪ω✪)
文本目录: ❄️一、习题一(检查两颗树是否相同): ▶ 思路: ▶ 代码: ❄️二、习题二(另一棵树的子树): ▶ 思路: ▶ 代码: ❄️三、习题三(翻转二叉树): ▶ 思路: ▶ 代…...

js 时间戳转日期格式
timestampToDate(obj.project_time), import moment from “moment”; const timestampToDate (timestamp: any) > { const date new Date(timestamp * 1000); const newDate moment(date).format(“YYYY-MM-DD”); return newDate; // 使用Intl.DateTimeFormat进行格式…...

基于人工智能的自动驾驶系统项目教学指南
自动驾驶系统是人工智能的一个核心应用领域,涉及多个学科的交叉:从计算机视觉、深度学习、传感器融合到控制系统,自动驾驶项目可以提供高度的挑战性和实践意义。在这篇文章中,我们将构建一个基于深度学习的自动驾驶系统的简化版本…...
[Linux#49][UDP] 2w字详解 | socketaddr | 常用API | 实操:实现简易Udp传输
目录 套接字地址结构(sockaddr) 1.Socket API 2.sockaddr结构 3. sockaddr、sockaddr_in 和 sockaddr_un 的关系 sockaddr 结构体 sockaddr_in 结构体(IPv4 套接字地址) sockaddr_un 结构体(Unix域套接字地址&a…...

期权组合策略有什么风险?期权组合策略是什么?
今天期权懂带你了解期权组合策略有什么风险?期权组合策略是什么?期权组合策略是通过结合不同期权合约(如看涨期权和看跌期权),以及标的资产(如股票)来实现特定投资目标的策略。 期权组合策略市…...

从Zotero6到Zotero7的数据迁移尝试?(有错勿喷,多多指教!)
从Zotero6到Zotero7的数据迁移尝试 0 前言 之前在主机上一直用的Zotero6(实验室主机),最近发现在个人笔记本上看论文更频繁,尝试重新部署Zotero,才发现竟然更新了!所以这里简单记录一下数据迁移过程&…...
快速排序(分治思想)
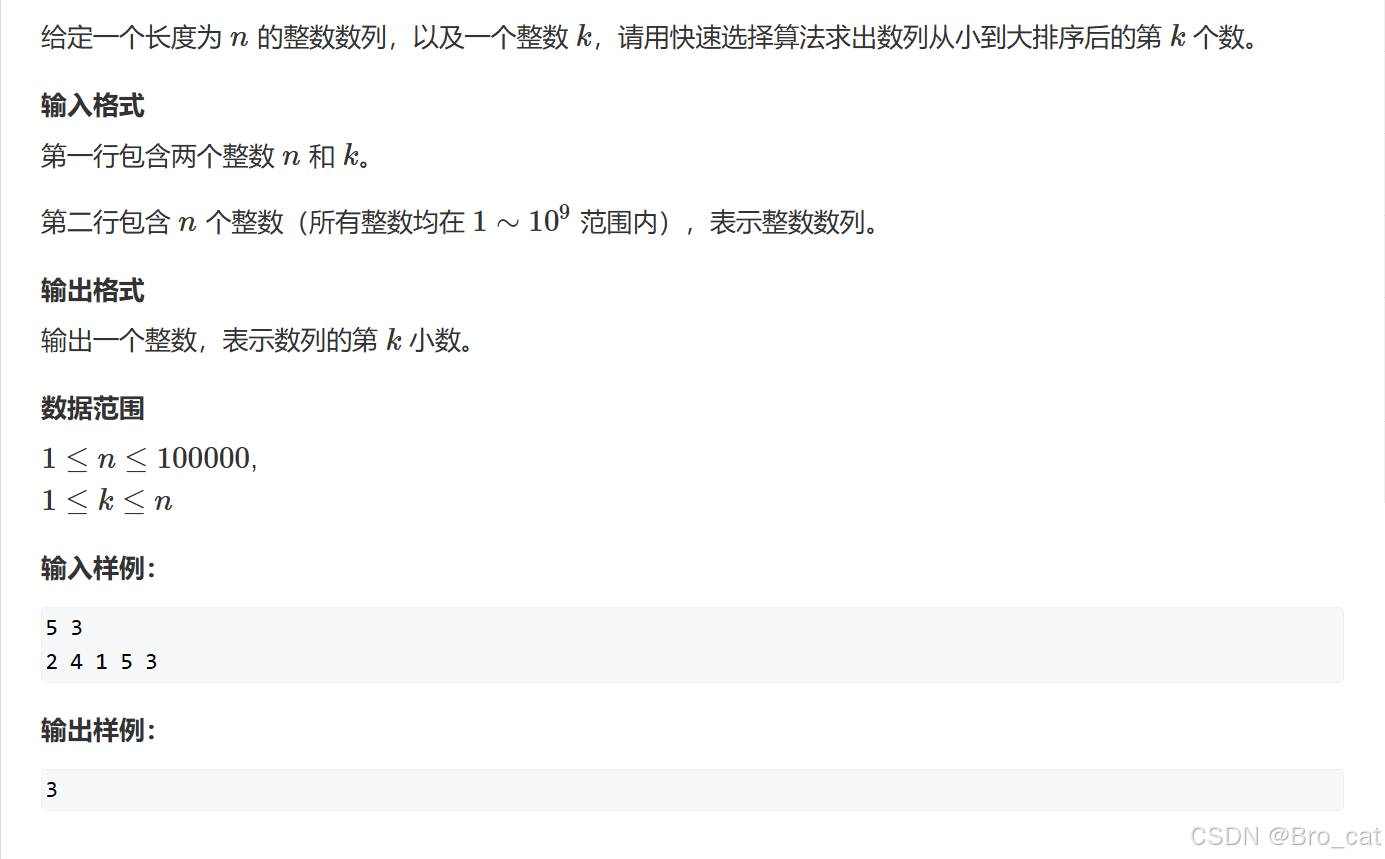
什么是快速排序 快速排序(Quick Sort)是一种广泛使用的高效排序算法,由计算机科学家托尼霍尔在1960年提出。它采用分治法(Divide and Conquer)策略,将一个大数组分为两个小数组,然后递归地对这两…...

JAVA相关知识
JAVA基础知识 说一下对象创建的过程? 类加载检查:当Java虚拟机(JVM)遇到一个类的new指令时,它首先检查这个类是否已经被加载、链接和初始化。如果没有,JVM会通过类加载器(ClassLoaderÿ…...

详解TCP的三次握手
TCP(三次握手)是指在建立一个可靠的传输控制协议 (TCP) 连接时,客户端和服务器之间的三步交互过程。这个过程的主要目的是确保连接是可靠的、双方的发送与接收能力是正常的,并且可以开始数据传输。下面是对每个步骤的详细解释&…...
Java面试篇基础部分-Java创建线程详解
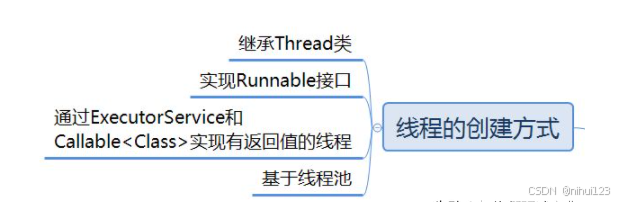
导语 多线程的方式能够在操作系统的多核配置上更好的利用服务器的多个CPU的资源,这样的操作可以使得程序运行起来更加高效。Java中多线程机制提供了在一个进程内并发去执行多个线程,并且每个线程都并行的去执行属于线程处理的自己的任务,这样可以提高程序的执行效率,让…...
Ubuntu 20.04/22.04无法连接网络(网络图标丢失、找不到网卡)的解决方案
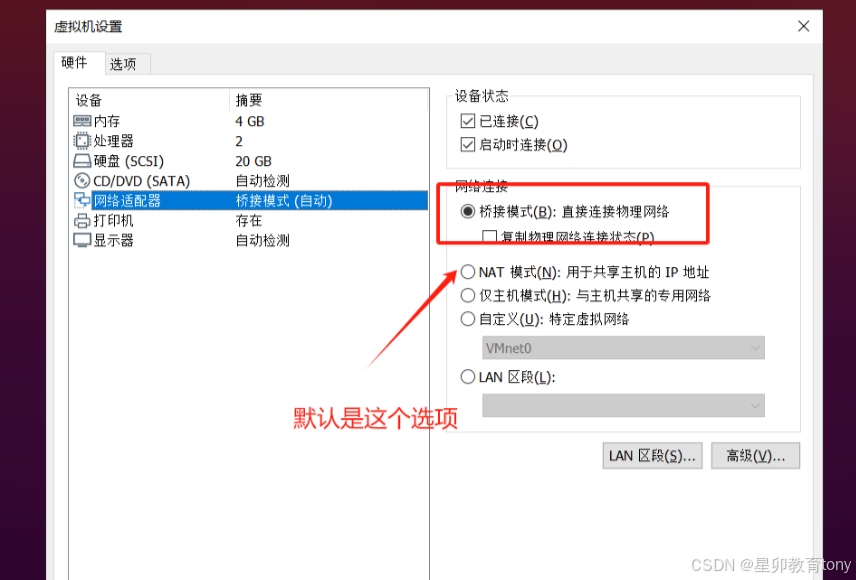
问题复述: Ubuntu 20.04无法连接到网络,网络连接图标丢失,网络设置中无网络设置选项。 解决方案 对于Ubuntu 20.04而言:逐条执行 sudo service network-manager stopsudo rm /var/lib/NetworkManager/NetworkManager.statesudo…...
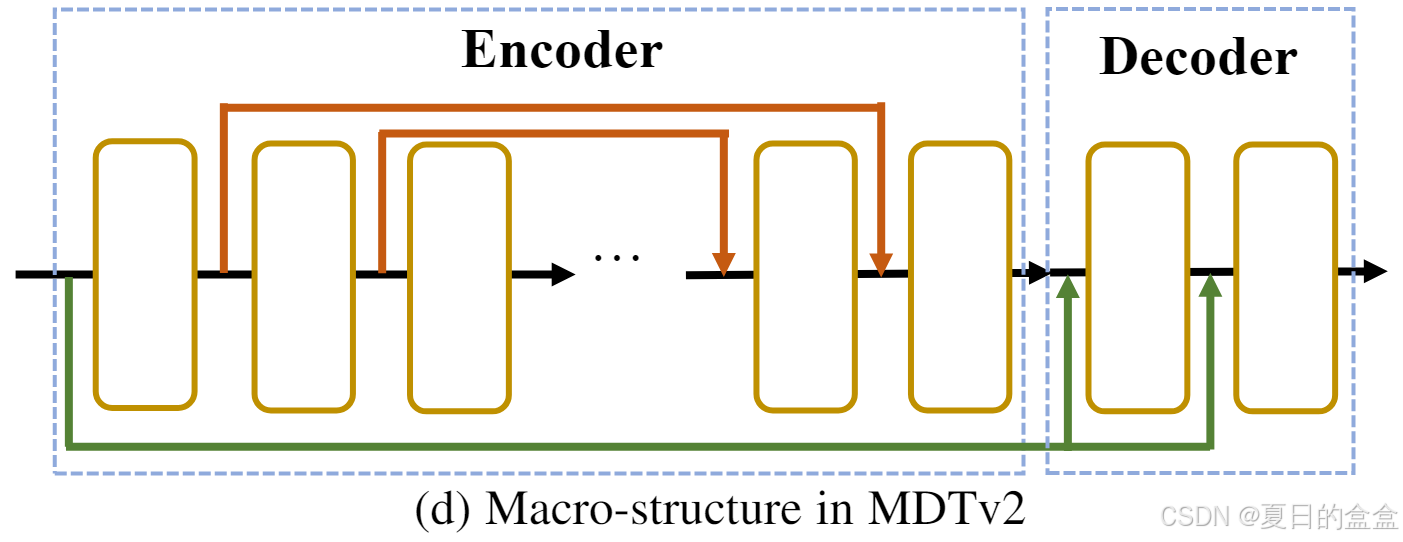
《MDTv2- Masked Diffusion Transformer is a Strong Image Synthesizer》
论文摘要 论文提出了一种名为**Masked Diffusion Transformer (MDT)**的新模型,旨在增强扩散概率模型(DPMs)在图像合成中的上下文推理能力。通过引入掩码潜在建模方案,MDT能够显著提升DPMs在图像中对象部分之间关系的学习能力&am…...

算法 - 二分查找
算法 - 二分查找 今天继续八股文学习,看一下比较常规的几个算法 二分查找是一个基于分治策略的搜索方法,简单的理解就是每次都缩小一轮搜索范围,从中间search一次,直到搜索到结果或者为空为止。 基本思路(设一个有序的…...

Python知识点:如何使用Python进行图像批处理
在Python中进行图像批处理可以使用多种库,如 Pillow、OpenCV 和 imageio。这些库可以用来执行各种图像处理任务,如调整大小、裁剪、旋转、滤镜应用等。以下是使用这些库进行图像批处理的示例。 使用 Pillow 进行图像批处理 Pillow 是一个功能强大的图像…...

数据结构实验1
实验题1:求1到n的连续整数和 题目描述 编写一个程序,对于给定的正整数n,求12…十n,采用逐个累加与(n1)/2(高斯法)两种解法。对于相同的n,给出这两种解法的求和结果和求解时间,并用相关数据进行测试。 运行代码 //实验题1:求1到n的连续整数和 #includ…...

使用Postman+JMeter进行简单的接口测试
以前每次学习接口测试都是百度,查看相关人员的实战经验,没有结合自己公司项目接口真正具体情况。 这里简单分享一下公司项目Web平台的一个查询接口,我会使用2种工具Postman和JMeter如何对同一个接口做调试。 准备工作 首先,登录公…...

基于 SpringBoot 的车辆充电桩管理系统
专业团队,咨询就送开题报告 摘 要 随着信息化时代的到来,管理系统都趋向于智能化、系统化,车辆充电桩管理系统也不例外,但目前国内仍都使用人工管理,市场规模越来越大,同时信息量也越来越庞大,…...
centos7.9安装clamav教程
本章教程主要记录在centos7.9安装clamav过程。 ClamAV(Clam AntiVirus)是一个开源的防病毒软件工具,主要用于检测和消除恶意软件。它最初由 Tomasz Kojm 于 2001 年开发,并由 Cisco Systems 维护和支持。ClamAV 广泛应用于邮件网关、文件服务器和其他需要防病毒保护的环境中…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
