【C++】——vector模拟实现和迭代器失效问题
文章目录
- 模拟实现
- vector基本成员变量
- vector的构造与析构
- vector迭代器
- vector容量
- vector元素访问
- vector修改操作
- vector迭代器失效问题
- 什么是迭代器失效
- 1.插入元素导致迭代器失效
- 2.删除元素导致迭代器失效
- 3.重新分配空间导致迭代器失效
- 如何解决迭代器失效问题
模拟实现
vector基本成员变量

namespace sg
{template<class T>class vector{
public:typedef T* iterator;typedef const T* const_iterator;
private:iterator _start = nullptr;iterator _finish = nullptr;iterator _end_of_storage = nullptr;}
};
这里我把成员改成与迭代器相关,更方便我们接下来的使用
vector的构造与析构
//构造函数
vector(const vector<T>& v)
{reserve(v.size()); // 开辟一个空间for (auto& e : v){push_back(e);}
}
//析构函数
~vector()
{if (_start) // 如果_start不为空就析构{delete[] _start;_start = _finish = _end_of_storage = nullptr;}
}
vector迭代器
iterator begin()
{return _start;
}
iterator end()
{return _finish;
}
const_iterator begin() const
{return _start;
}
const_iterator end() const
{return _finish;
}
vector容量
bool empty()
{return _start == _finish;
}
void reserve(size_t n)
{size_t old_size = size();T* tmp = new T[n];memcpy(tmp, _start, size() * sizeof(T));delete[] _start;_start = tmp;_finish = tmp + old_size;_end_of_storage = _start + n;
}
size_t size()
{return _finish - _start;
}size_t capacity()
{return _end_of_storage - _start;
}void resize(size_t n, T val = T())
{if (n < size()){_finish = _start + n;}else{reserve(n);while (_finish < _start + n){*_finish = val;++_finish;}}
}
vector元素访问
T& operator[](size_t i)
{assert(i < size());return _start[i];
}
vector修改操作
void push_back(const T& x)
{if (_finish == _end_of_storage){reserve(capacity() == 0 ? 4 : capacity() * 2);}*_finish = x;_finish++;
}
void pop_back()
{assert(!empty());--_finish;
}
iterator insert(iterator pos, const T& x)
{assert(pos >= _start);assert(pos <= _finish);//扩容if (_finish == _end_of_storage){size_t len = pos - _start;reserve(capacity() == 0 ? 4 : capacity() * 2);pos = _start + len;}iterator end = _finish - 1;while (end >= pos){*(end + 1) = *end;--end;}*pos = x;++_finish;return pos;
}
void erase(iterator pos)
{assert(pos >= _start);assert(pos < _finish);iterator it = pos + 1;while (it != end()){*(it - 1) = *it;++it;}--_finish;
}
vector迭代器失效问题
迭代器失效的本质是因为vector的内存管理机制和对动态数组的封装方式。vector的某些操作会导致其底层数组的重新分配,所以原有的迭代器会失效。
什么是迭代器失效
迭代器失效的常见情况:
- 插入元素:在vector末尾插入元素,除了指向最后一个元素的迭代器以外,其他迭代器依旧有效
如果在其他位置插入,则指向该插入位置的迭代器和其之后的所有迭代器失效- 删除元素:删除元素后,被删除和删除之后的所有迭代器都会失效
- 重新分配:当vector的大小超过当前容量时,它可能分配需要更大的空间进行存储元素,这种重新分配会导致所有迭代器、指针、引用失效
注意:vector的迭代器失效也和编译器环境有关,有关指报错和运行。在Linux下,g++对于迭代器失效的检查就没这么严格,一般迭代器失效也还能运行,不过运行结果会出错。
1.插入元素导致迭代器失效
int main()
{vector<int> v1{ 1,2,3,4,5 };auto it = v1.begin();v1.insert(v1.begin(), 99); // 在第一个位置插入元素while (it != v1.end()){cout << *it << " ";++it;}cout << endl;return 0;
}

插入和删除同理,这里我已删除为例

2.删除元素导致迭代器失效
int main()
{vector<int> v1{ 1,2,3,4,5 };auto it = v1.begin();v1.erase(v1.begin()); // 删除第一个元素while (it != v1.end()){cout << *it << " ";++it;}cout << endl;return 0;
}

3.重新分配空间导致迭代器失效
int main()
{vector<int> v1{ 1,2,3,4,5 };auto it = v1.begin();v1.resize(20, 10); // 容量不够,重新分配空间,又叫异地扩容while (it != v1.end()){cout << *it << " ";++it;}cout << endl;return 0;
}


如何解决迭代器失效问题
string迭代器失效原因和vector异地扩容类似,需要注意。
解决办法:在使用前重新赋值
int main()
{vector<int> v1{ 1,2,3,4,5 };auto it = v1.begin();v1.resize(20, 10); // 容量不够,重新分配空间,又叫异地扩容it = v1.begin(); // 使用前重新赋值while (it != v1.end()){cout << *it << " ";++it;}cout << endl;return 0;
}
相关文章:

【C++】——vector模拟实现和迭代器失效问题
文章目录 模拟实现vector基本成员变量vector的构造与析构vector迭代器vector容量vector元素访问vector修改操作 vector迭代器失效问题什么是迭代器失效1.插入元素导致迭代器失效2.删除元素导致迭代器失效3.重新分配空间导致迭代器失效 如何解决迭代器失效问题 模拟实现 vector…...

USB 3.1 标准 A 型连接器及其引脚分配
USB 3.1 标准 A 型连接器 USB 3.1 标准 A 型连接器被定义为主机连接器。它具有与 USB 2.0 标准 A 型连接器相同的配合接口,但增加了另外两对差分信号和一个接地引脚。 USB 3.1 标准 A 型插座可以接受 USB 3.1 标准 A 型插头或 USB 2.0 标准 A 型插头。类似地&…...

机器学习文献|基于循环细胞因子特征,通过机器学习算法预测NSCLC免疫治疗结局
今天我们一起学习一篇最近发表在Journal for immunotherapy of cancer (IF 10.9)上的文章,Machine learning for prediction of immunotherapeutic outcome in non-small-cell lung cancer based on circulating cytokine signatures[基于循环…...

Qt 实现自定义截图工具
目录 Qt 实现自定义截图工具实现效果图PrintScreen 类介绍PrintScreen 类的主要特性 逐步实现第一步:类定义第二步:初始化截图窗口第三步:处理鼠标事件第四步:计算截图区域第五步:捕获和保存图像 完整代码PrintScreen.…...

第15-05章:获取运行时类的完整结构
我的后端学习大纲 我的Java学习大纲 6.1.第一组方法API: 1.API列表:java.lang.Class 类: 2.代码测试: public class ReflectionUtils{ puvblic static void main(String[] args){}// 第一组Testpublic void api_01{//上面截图的代码......…...

【Kubernetes】K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制
K8s 的鉴权管理(二):基于属性 / 节点 / Webhook 的访问控制 1.基于属性的访问控制(ABAC 鉴权)2.基于节点的访问控制(node 鉴权)2.1 读取操作2.2 写入操作 3.基于 Webhook 的访问控制3.1 基于 We…...

Java面试、技巧、问题、回复,资源面面观
入门 先了解一下面试流程 复习 Java 基础知识: 温习 Java 编程的核心概念,包括数据类型、变量、循环、数组和面向对象的编程原则。数据结构和算法: 加强您对 Java 编程中使用的基本数据结构和算法的理解。练习编码: 在各种平台上解…...

深入理解Elasticsearch的`_source`字段与索引优化
在Elasticsearch (ES) 中,_source字段是一个关键组件,它不仅决定了数据的存储方式,还影响到查询时返回的内容。在某些场景下,我们可以通过配置_source来优化存储和性能,尤其是当我们希望减少存储空间或避免返回某些字段…...
Pikachu靶场
先来点鸡汤,少就是多,慢就是快。 环境搭建 攻击机kali 192.168.146.140 靶机win7 192.168.146.161 下载zip,pikachu - GitCode 把下载好的pikachu-master,拖进win7,用phpstudy打开网站根目录,.....再用…...

TS axios封装
方式一 service/request/request.ts import axios from axios import { ElLoading } from element-plus import type { AxiosRequestConfig, AxiosInstance, AxiosResponse } from axios import type { ILoadingInstance } from element-plus/lib/el-loading/src/loading.typ…...

学会使用西门子博途Startdrive中的测量功能
工程师在驱动调试过程中,往往需要对驱动系统的性能进行分析及优化,比如说借助于调试软件中的驱动器测量功能,可以得到驱动系统的阶跃响应、波特图等,以此为依据工程师可以调整速度控制器、电流控制器的相关参数,使驱动…...
Spring Security认证与授权
1 Spring Security介绍 Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方案的安全框架。由于它是Spring生态系统中的一员,因此它伴随着整个Spring生态系统不断修正、升级,在spring boot项目中加入springsecurity更是…...
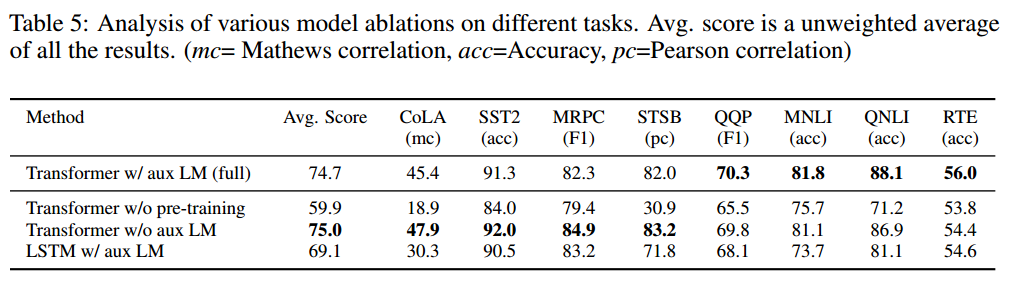
速通GPT:Improving Language Understanding by Generative Pre-Training全文解读
文章目录 速通GPT系列几个重要概念1、微调的具体做法2、任务感知输入变换3、判别式训练模型 Abstract概括分析和观点1. 自然语言理解中的数据问题2. 生成预训练和监督微调的结合3. 任务感知输入变换4. 模型的强大性能 Introduction概括分析和观点1. 自然语言理解的挑战在于对标…...
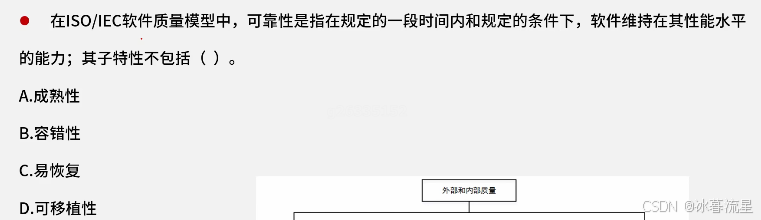
软件质量保证例题
答案:D 软件质量保证 功能性 适合性 准确性 互操作性 安全保密性 依从性 可靠性 成熟性 容错性 易恢复性 易用性 易理解性 易学性 易操作性 效率 时间特性 资源利用性 维护性 易分析性 易改变性 稳定性 易测试性 可移植性 适应性 易安装性 一致性 易替换…...
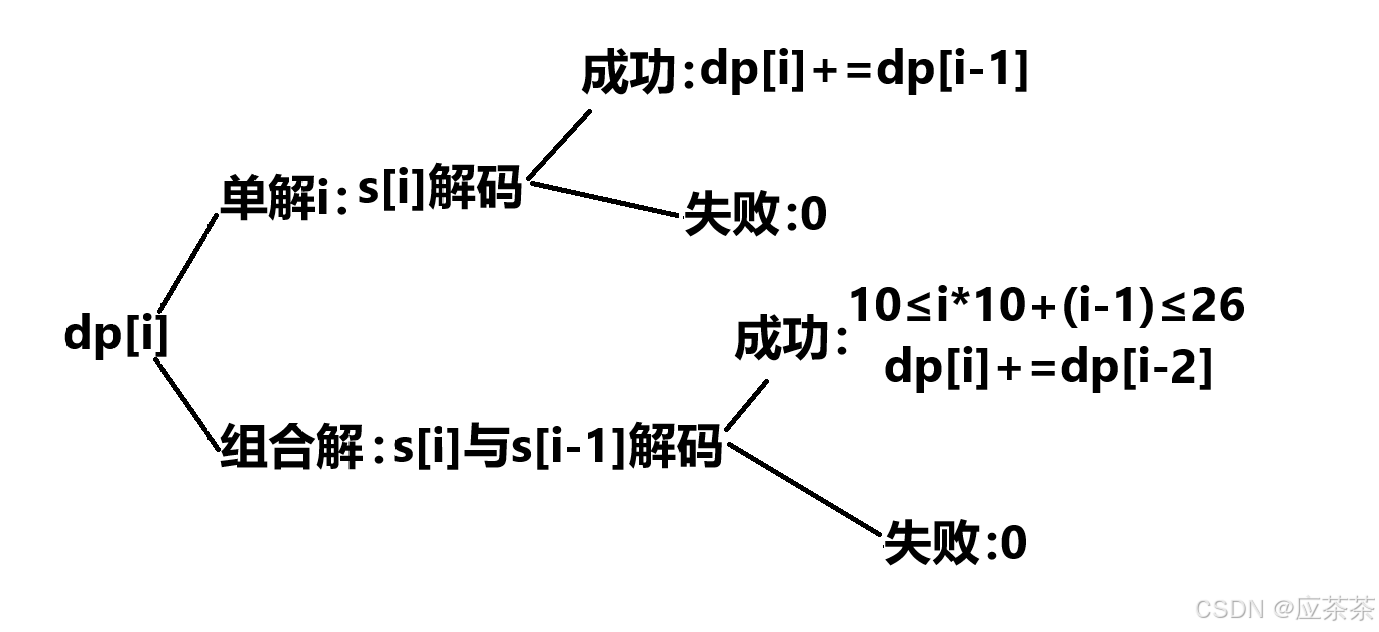
动态规划算法---04.斐波那契数列模型_解码方法_C++
题目链接:91. 解码方法 - 力扣(LeetCode)https://leetcode.cn/problems/decode-ways/description/ 一、题目解析 题目: 题目大意:从题目中我们可以知道,解码就是在字符串s中由‘1’到‘26’的字符可以转化…...

crm如何做私域运营?
流量获取的挑战日益增加,客户线索成本高、客户资源流失严重、转化率低,因此,私域流量管理已成为关键。 当前挑战 1、公域流量难以整合:外部流量分散,难以有效汇总和沉淀。 2、私域运营体系缺失:缺乏有效沟…...
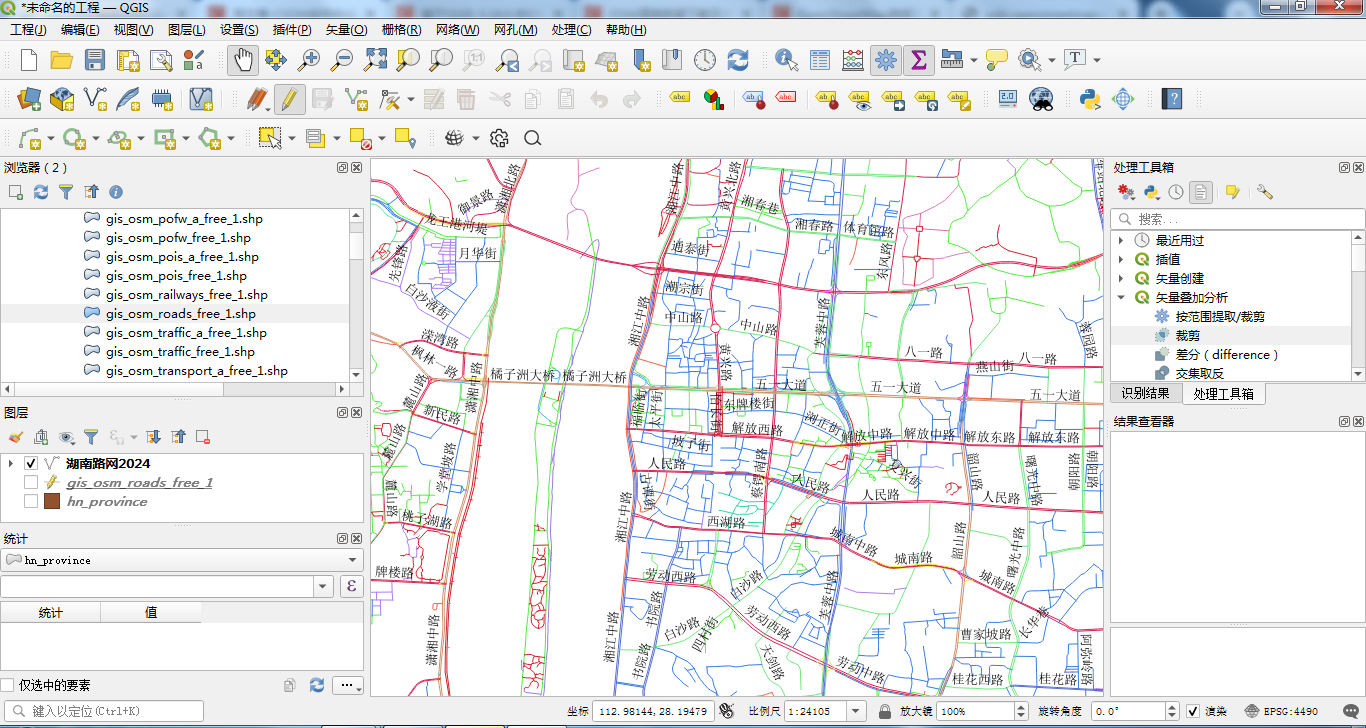
基于QGIS 3.16.0 的OSM路网矢量范围裁剪实战-以湖南省为例
目录 前言 一、相关数据介绍 1、OMS路网数据 2、路网数据 3、路网图层属性 二、按省域范围进行路网裁剪 1、裁剪范围制定 2、空间裁剪 3、裁剪结果 三、总结 前言 改革开放特别是党的十八大以来,我国公路发展取得了举世瞩目的成就。国家高速公路网由“7 射…...
WPF 手撸插件 八 依赖注入
本文内容大量参考了:https://www.cnblogs.com/Chary/p/11351457.html 而且这篇文章总结的非常好。 1、注意想使用Autofac,Autofac是一个轻量级、高性能的依赖注入(DI)框架,主要用于.NET应用程序的组件解耦和…...

走进低代码报表开发(一):探秘报表数据源
在前文当中,我们对勤研低代码平台的流程设计功能进行了介绍。接下来,让我们一同深入了解在企业日常运营中另一个极为常见的报表功能。在当今数字化时代,高效的报表生成对于企业的决策至关重要。勤研低代码开发平台能够以卓越的性能和便捷的操…...
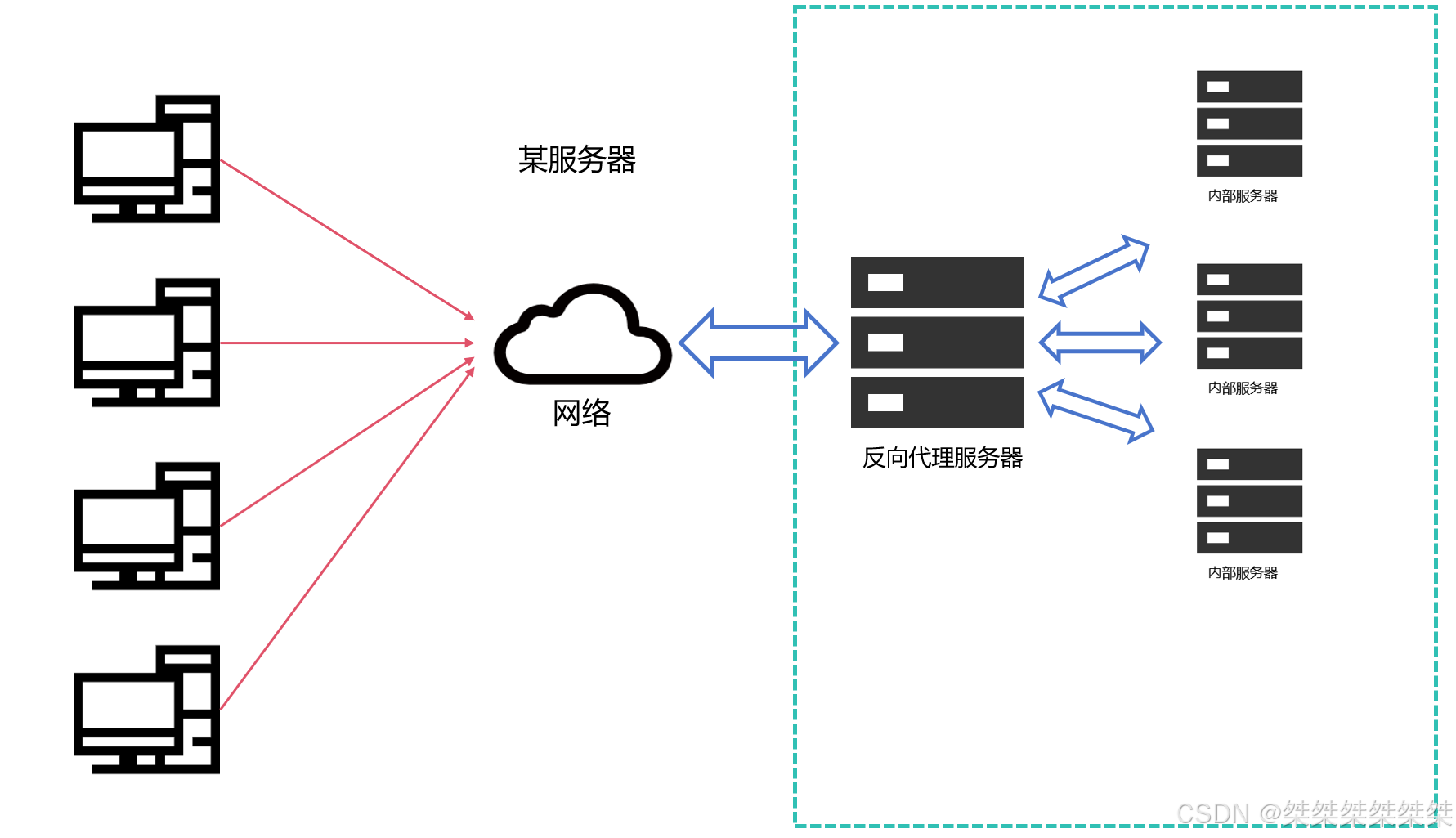
代理服务器及其原理
代理服务器的代理可以分为正向代理和反向代理,本篇将讲解这两种代理方式的原理,以及对应的功能特点和应用场景。最后还对比和 NAT 和代理服务器的区别。 目录 正向代理 工作原理 功能特点 应用场景 反向代理 基本原理 应用场景 NAT和代理服务器…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
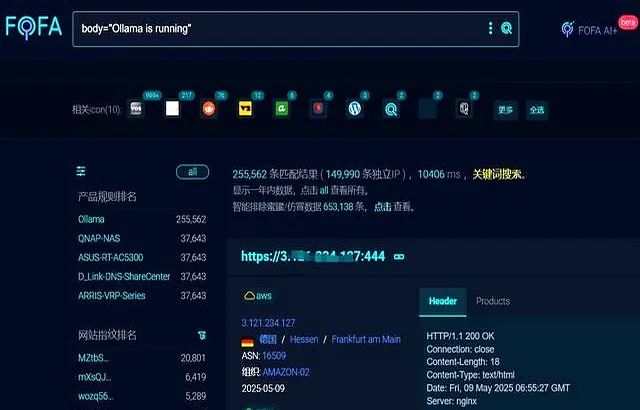
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...
