代码随想录算法训练营第二十六天 | 39. 组合总和,40.组合总和II,131.分割回文串
一、参考资料
组合总和
题目链接/文章讲解:https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html
视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ
组合总和II
题目链接/文章讲解:https://programmercarl.com/0040.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CII.html
视频讲解:https://www.bilibili.com/video/BV12V4y1V73A
分割回文串
题目链接/文章讲解:https://programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html
视频讲解:https://www.bilibili.com/video/BV1c54y1e7k6
二、LeetCode39. 组合总和
https://leetcode.cn/problems/combination-sum/description/
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
本题搜索的过程抽象成树形结构如下:
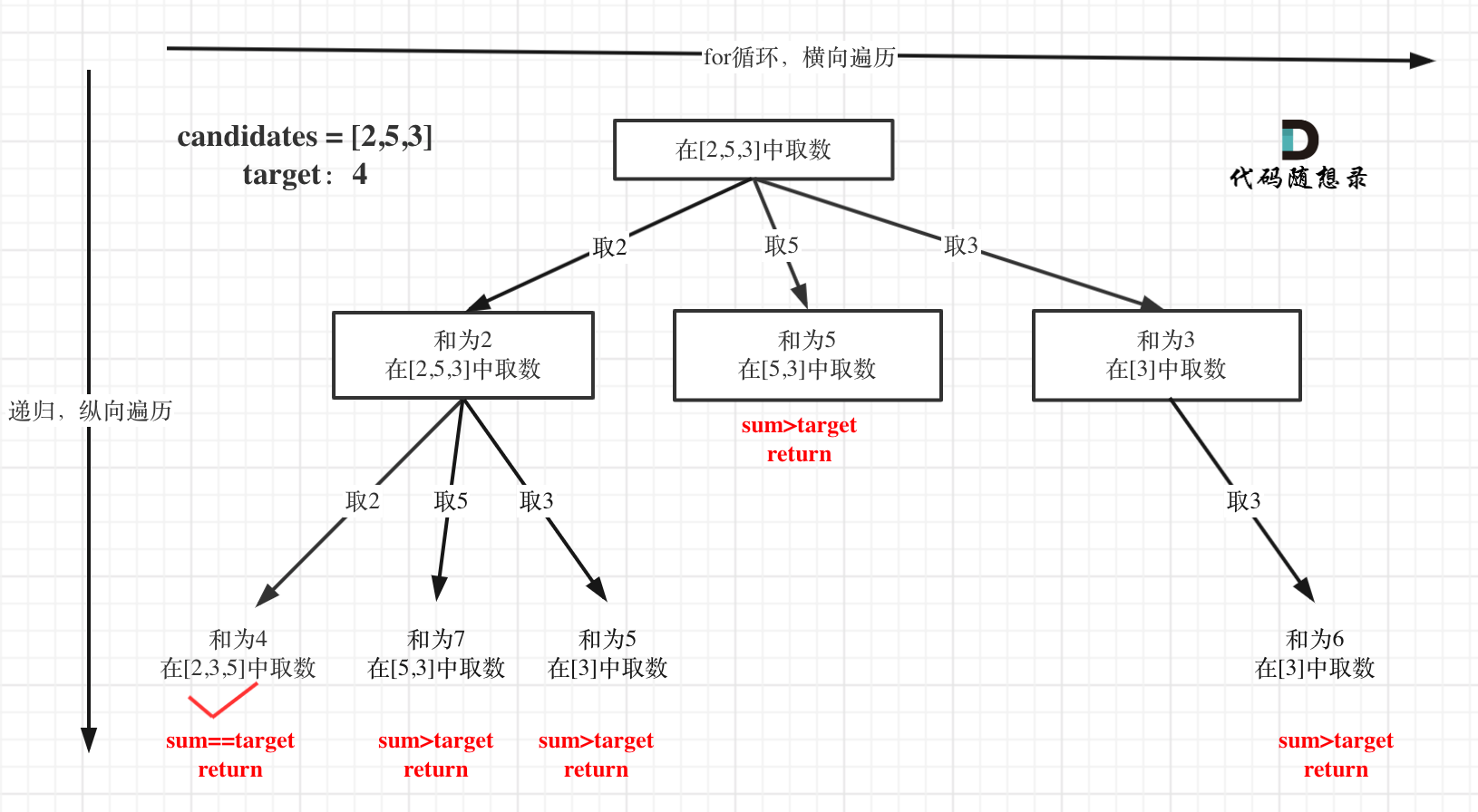
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
而在77.组合 (opens new window)和216.组合总和III (opens new window)中都可以知道要递归K层,因为要取k个元素的组合。
我也能自己写出代码啦,模板真香
class Solution {
private:vector<int> path;vector<vector<int>> res;void backtracking(vector<int> candidates, int target, int sum, int startIndex) {if (sum > target) return ;if (sum == target) {res.push_back(path);return ;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数path.pop_back();sum -= candidates[i];}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates, target, 0, 0);return res;}
};剪枝优化(这里没有详细研究,大体思路还是在循环的地方提前终止):
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
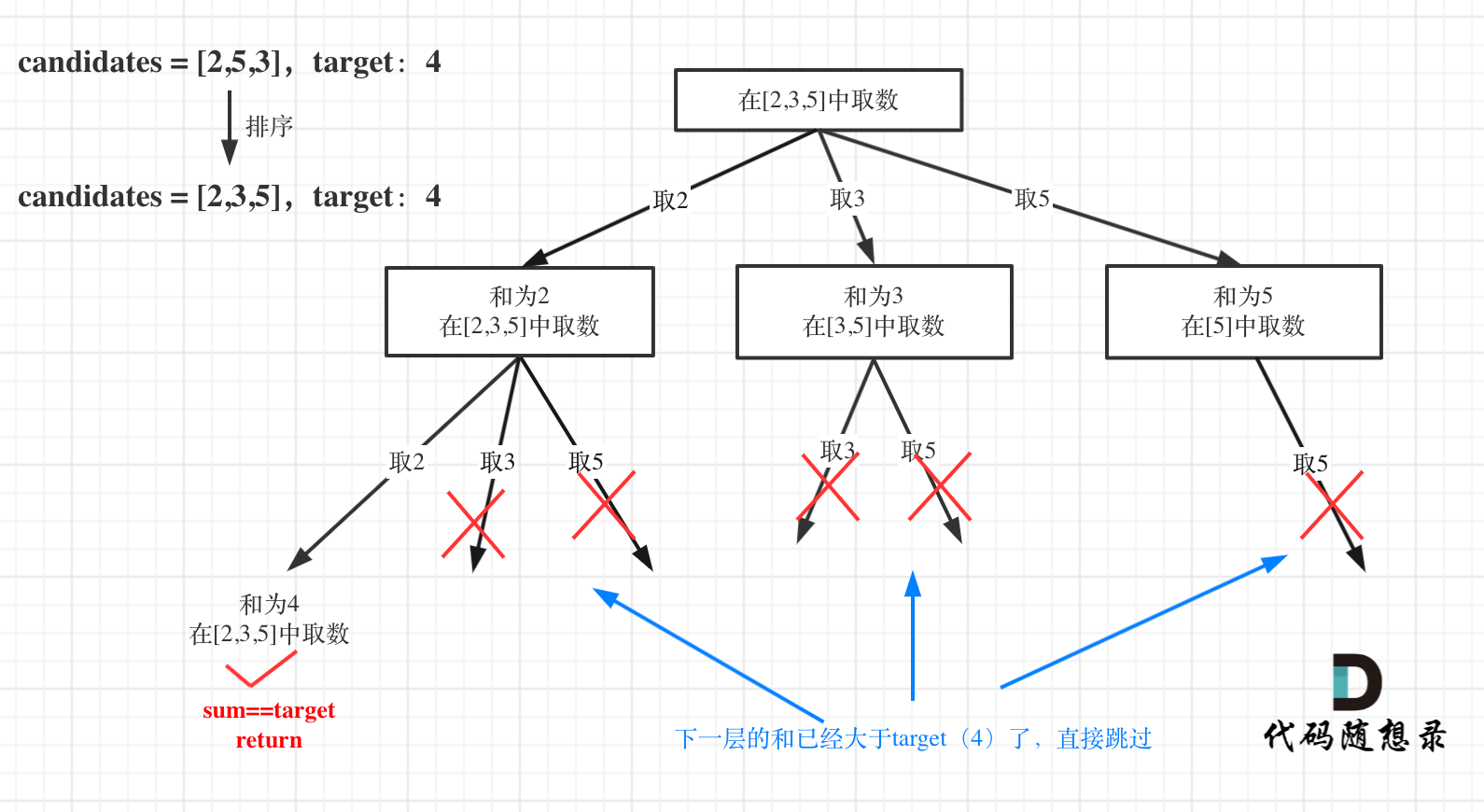
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) {result.push_back(path);return;}// 如果 sum + candidates[i] > target 就终止遍历for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i);sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();sort(candidates.begin(), candidates.end()); // 需要排序backtracking(candidates, target, 0, 0);return result;}
};在求和问题中,排序之后加剪枝是常见的套路!
三、LeetCode40.组合总和II
https://leetcode.cn/problems/combination-sum-ii/description/
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]
提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
先排序!再树层去重
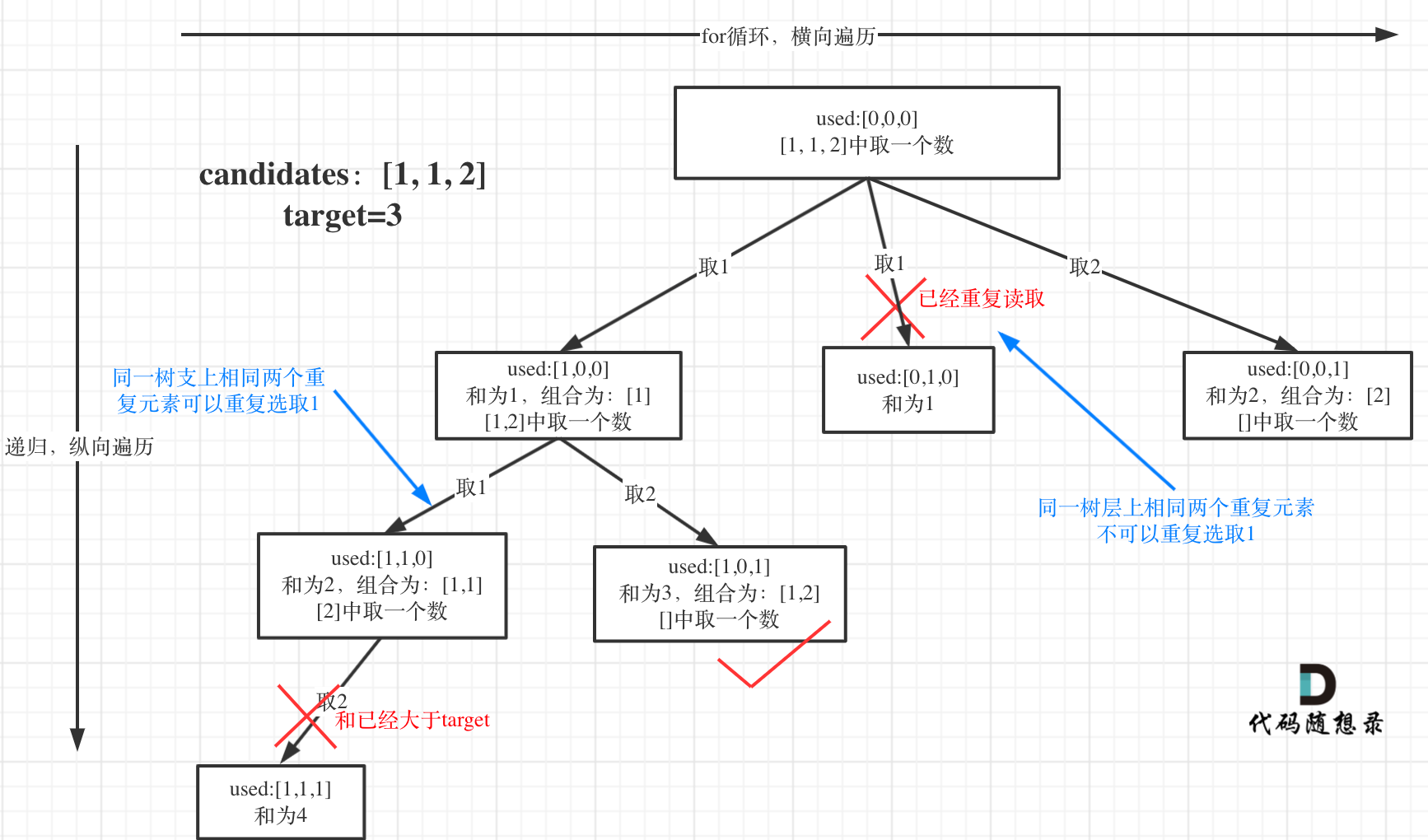
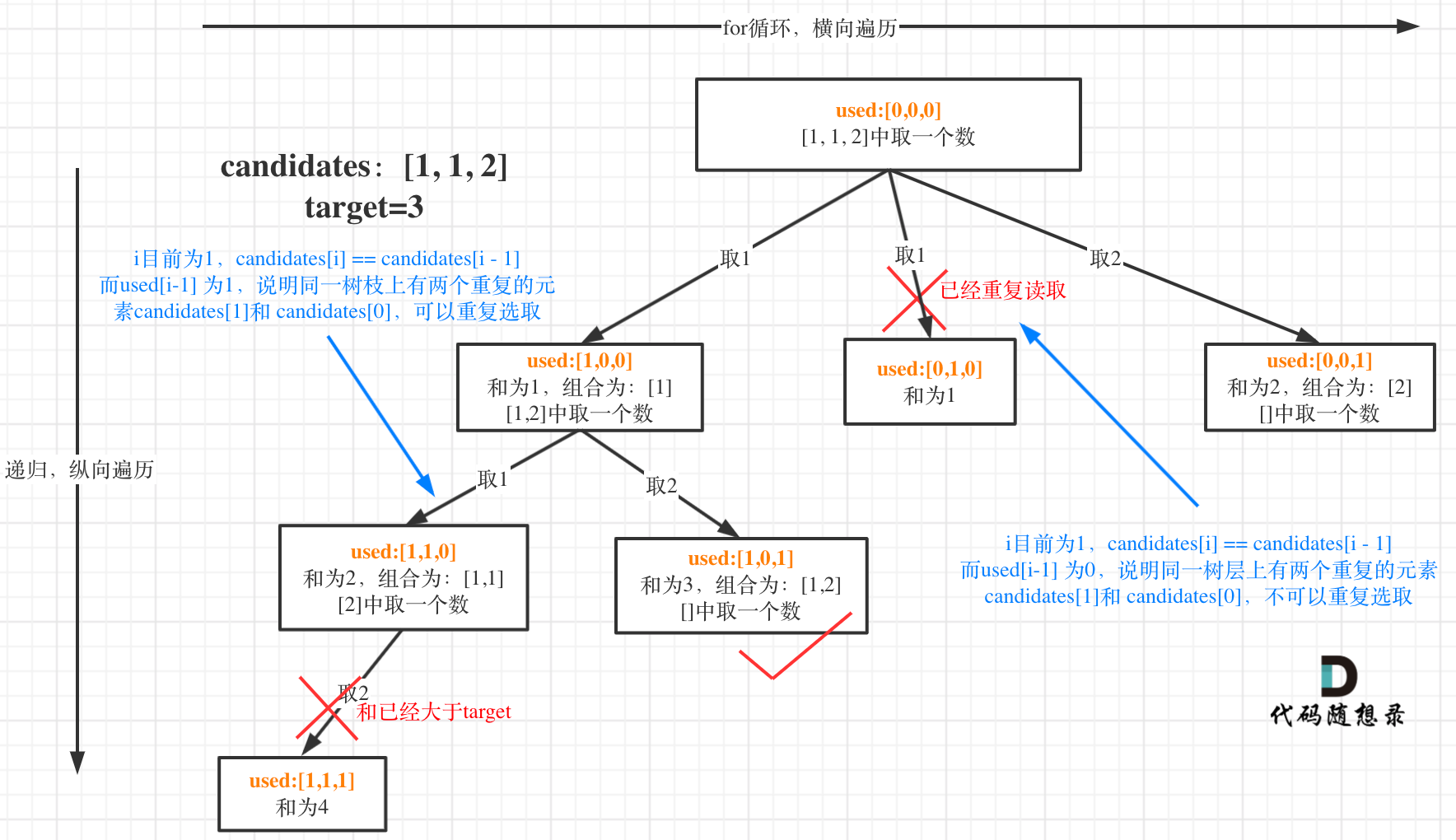
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
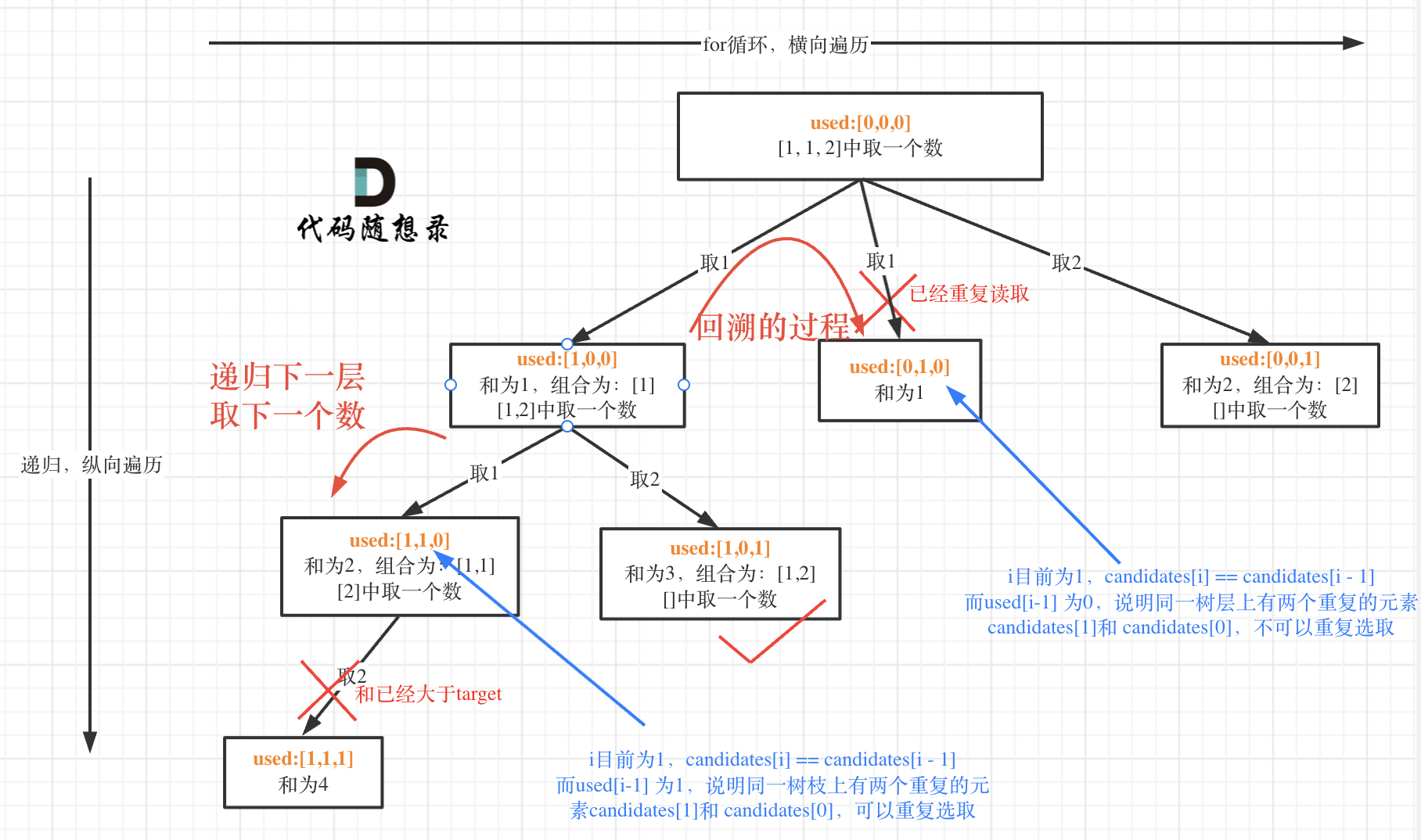
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序,让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};我写的如下~
class Solution {
private:vector<int> path;vector<vector<int>> res;void backtracking(vector<int> candidates, int target, int sum, int startIndex, vector<bool> used) {if (sum > target) return ;if (sum == target) {res.push_back(path);return ;}for (int i = startIndex; i < candidates.size(); i++) {if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;sum += candidates[i];used[i] = true;path.push_back(candidates[i]);backtracking(candidates, target, sum, i + 1, used);path.pop_back();used[i] = false;sum -= candidates[i];}}
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return res;}
};四、LeetCode131.分割回文串
https://leetcode.cn/problems/palindrome-partitioning/description/
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a" 输出:[["a"]]
提示:
1 <= s.length <= 16
s 仅由小写英文字母组成
带注释版:
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经填在的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};优化后的代码就没详细学了
我能自己写出这个题的代码,已经觉得自己真的进步很大了:
class Solution {
private:vector<string> path;vector<vector<string>> res;bool isPalinedromic(string s, int begin, int end) {for (int i = begin, j = end; i < j; i++, j--) {if (s[i] != s[j]) return false;}return true;}void backtracking (string s, int startIndex) {if(startIndex > s.size()) return ;if (startIndex == s.size()) {res.push_back(path);return ;}for(int i = startIndex; i < s.size(); i++) {if(isPalinedromic(s, startIndex, i)) {string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else continue;backtracking(s, i + 1);path.pop_back();}}
public:vector<vector<string>> partition(string s) {backtracking(s, 0);return res;}
};今日总结:
题目确实是当天写完的,只是博客没有及时写
感觉到自己真的进步好多了,能够理解懂视频的题目讲解,经历一些debug后还能尝试控制时间的前提下独立完成代码。
今天的难点应该挺多的,我花了很多时间理解来着,讲解回文串分割的视频应该看了两遍。
另外今天的组合数一个不太容易想到题解的“去重”问题,也是挺困扰,希望真的掌握后能做到举一反三呢
继续加油哈小赵~
相关文章:

代码随想录算法训练营第二十六天 | 39. 组合总和,40.组合总和II,131.分割回文串
一、参考资料组合总和题目链接/文章讲解:https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html 视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ 组合总和II题目链接/文章讲解:https://programmercarl.com/004…...

vueday01-脚手架安装详细
一、vue脚手架安装命令npm i -g vue/cli 或 yarn global add vue/cli安装上面的工具,安装后运行 vue --version ,如果看到版本号,说明安装成功或 vue -V工具安装好之后,就可以安装带有webpack配置的vue项目了。创建项目之前&#…...
)
初识cesium3d(一)
使用ViteVue3.2Cesium。Vite需要Node.js版本14.18及以上版本。Vite命令创建的工程会自动生成vite.config.js文件,来配置一些相关的参数。 1、使用Vite创建vue3项目 # npm npm init vitelatest cesium-app -- --template vue # yarn yarn create vite cesium-app…...

点云转3D网格【Python】
推荐:使用 NSDT场景设计器 快速搭建 3D场景。 在本文中,我将介绍我的 3D 表面重建过程,以便使用 Python 从点云快速创建网格。 你将能够导出、可视化结果并将结果集成到您最喜欢的 3D 软件中,而无需任何编码经验。 此外࿰…...
【OpenCV图像处理系列一】OpenCV开发环境的安装与搭建(Ubuntu + Window都适用)
🔗 运行环境:OpenCV,Ubuntu,Windows 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### &#x…...

【代码随想录】-动态规划专题
文章目录理论基础斐波拉契数列爬楼梯使用最小花费爬楼梯不同路径不同路径 II整数拆分不同的二叉搜索树背包问题——理论基础01背包二维dp数组01背包一维数组(滚动数组)装满背包分割等和子集最后一块石头的重量 II目标和一和零完全背包零钱兑换 II组合总和…...

c++数据类型 输入输出
C++语法 //常用包: iostream:cin cout endl cstdio:scanf printf algorithm:max min reverse swap cstring:memset memcpymemset(a,-1,sizeof a) 填充数组memcpy(b,a,sizeof a) 将a数组复制到b数组,长度是a数组字节长度 cmath:sin sqrt pow abs fabs编程是一种控制计…...
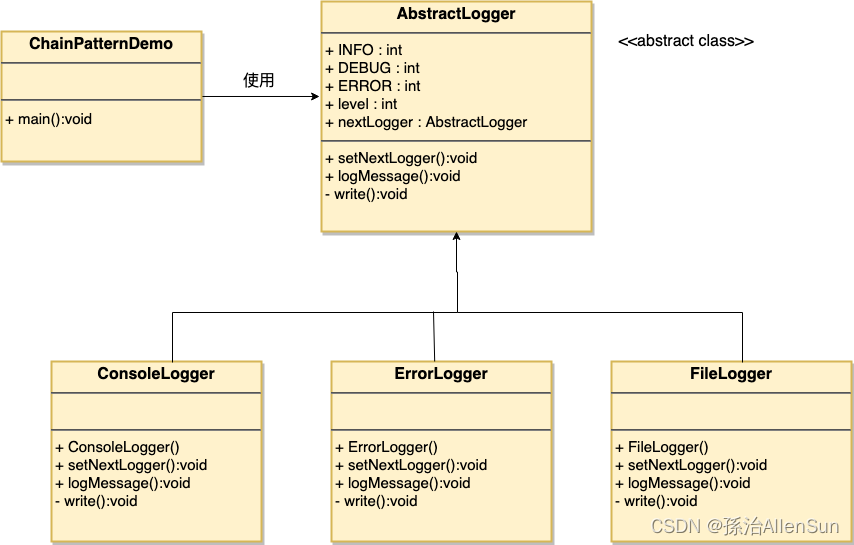
【设计模式-11】责任链模式
认识设计模式(十一)---责任链模式【一】责任链模式【二】介绍(1)意图(2)主要解决(3)何时使用(4)如何解决(5)关键代码(6&am…...
SpringBoot+Vue实现智能物流管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

【MT7628】MT7628如何修改串口波特率、调试串口物理口、使用UART3口
环境说明 sdk版本:Mediatek_ApSoC_SDK_4320_20150414.tar.bz2 芯片方案:MT7628A Uboot修改串口波特率方法 修改rt2880.h文件 修改include/configs/rt2880.h文件CONFIG_BAUDRATE宏的值 - #define CONFIG_BAUDRATE 57600 +#define CONFIG_BAUDRATE 115200 Kernel中修改串口波特…...

css盒模型介绍
在使用CSS进行网页布局时,我们一定离不开的一个东西————盒子模型。盒子模型,顾名思义,盒子就是用来装东西的,它装的东西就是HTML元素的内容。或者说,每一个可见的 HTML 元素都是一个盒子,下面所说的盒子…...

onetab 谷歌插件历史数据清除
文章目录方法1:测试也可以步骤1:批量执行点击步骤2:python 脚本模拟点击确定操作方法2:成功【推荐】步骤1:修改confirm,类似于hook操作步骤2:批量点击删除操作:onetab 谷歌插件历史数…...

GRBL源码简单分析
结构体说明 GRBL里面的速度规划是带运动段前瞻的,所以有规划运动段数据和微小运动段的区分 这里的“规划运动段”对应的数据结构是plan_block_t,前瞻和加减速会使用到,也就是通过解析G代码后出来的直接直线数据或是圆弧插补出来的拟合直线数据…...
)
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(谓语动词的情态)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

软考高级考试中有五大证书,其中哪个更值得考?
计算机软考属于专业技术人员职业资格水平评价类,是职业资格、专业技术资格(职称)和专业技术水平"三合一"的考试,是目前IT行业仅有的国家级考试。考试不受学历、专业、资历等条件限制。软考高级考试中有五大证书…...

FlexRay™ 协议控制器 (E-Ray)-04
网络管理 累积的网络管理 (NM) 向量位于网络管理寄存器 1 到网络管理寄存器 3 (NMVx (x = 1-3)) 中。【The accrued Network Management (NM) vector is located in the Network Management Register 1 to Network Management Register 3 (NMVx (x = 1-3)).】 网络管理向量 x…...

container_of 根据成员变量获得包含其的对象的地址!
写在前面 本系列文章的灵感出处均是各个技术书籍的读后感,详细书籍信息见文章最后的参考文献 CONTAINER_OF 在书中发现一个很有意思的宏,以此可以衍生出来其很多的用法,这个宏可以根据某个成员变量的地址得到包含这个成员变量地址的对象的…...
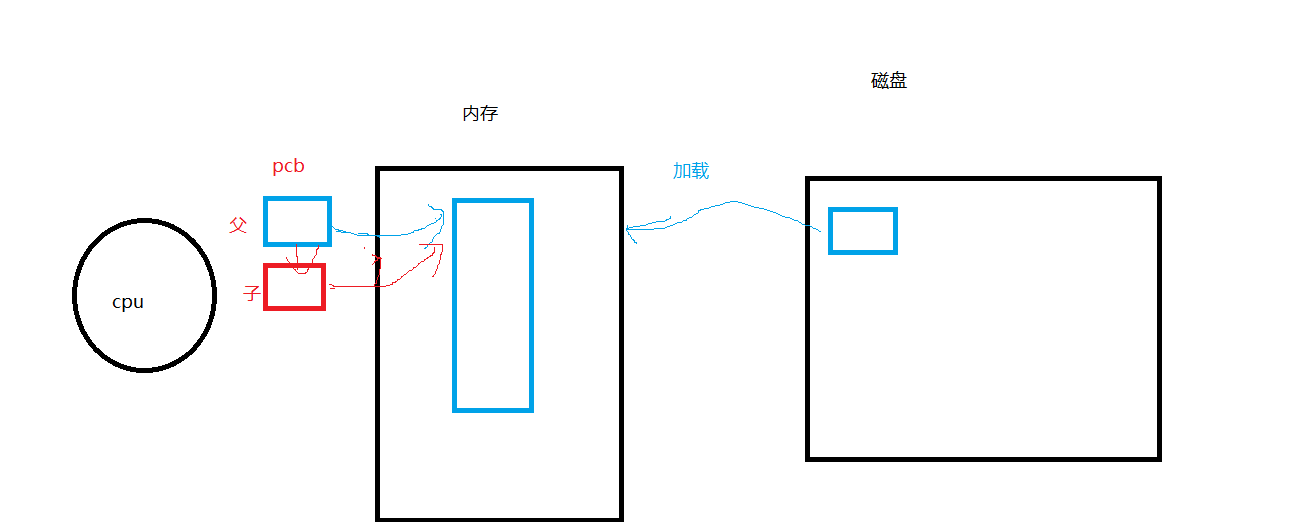
Linux进程概念
Linux进程概念前言冯诺依曼体系操作系统设计操作系统的目的如何理解OS是一款搞“管理”的软件?系统调用和库函数的概念进程的概念描述进程组织进程查看进程fork()前言 本篇博客主要介绍一些:冯诺依曼体系、OS的理解、进程的一些概…...
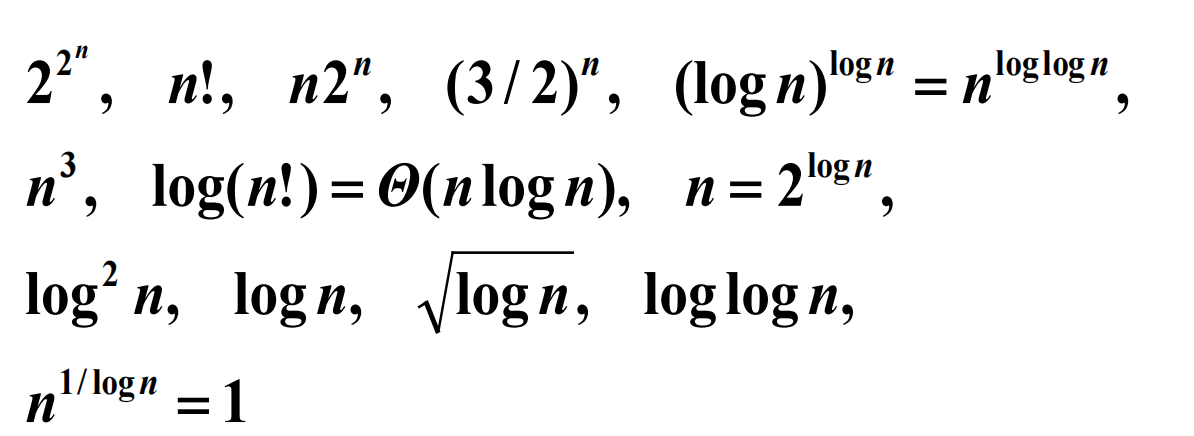
算法设计与分析
两个例子:调度问题与投资问题 例1:调度问题 问题 有 n 项任务,每项任务加工时间已知.从 0时刻开始陆续安排到一台机器上加工. 每个任务的完成时间是从 0 时刻到任务加工截止的时间. 求: 总完成时间(所有任务完成时间之和)最短…...
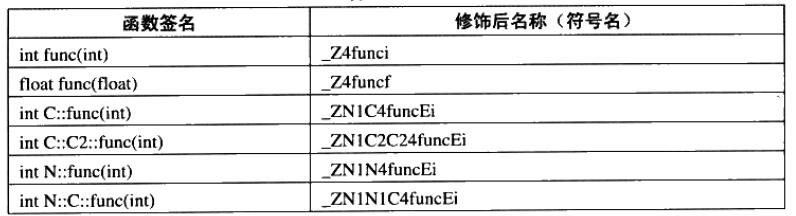
C++ 基础
命名空间 在 C/C 中,变量、函数和类都是大量存在的,这些变量、函数和类的名称将都存在全局作用域中,可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化,以避免命名冲突或名字污染,namespace 关键字的…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
