点云转3D网格【Python】

推荐:使用 NSDT场景设计器 快速搭建 3D场景。
在本文中,我将介绍我的 3D 表面重建过程,以便使用 Python 从点云快速创建网格。 你将能够导出、可视化结果并将结果集成到您最喜欢的 3D 软件中,而无需任何编码经验。 此外,我将为你提供一种生成多层次细节 (LoD) 的简单方法,如果想要创建实时应用程序(例如,使用 Unity 的虚拟现实),这很有用。
3D 网格是几何数据结构,通常由一堆连接的三角形组成,这些三角形明确描述了一个表面🤔。 它们用于从地理空间重建到 VFX、电影和视频游戏的广泛应用。 我经常在需要物理副本时创建它们,或者如果我需要在游戏引擎中集成环境,而在游戏引擎中,点云支持是有限的。

它们很好地融入了大多数软件专业人员的工作中。 最重要的是,如果你想探索 3D 打印的奇迹,需要能够从你拥有的数据生成一致的网格。 本文旨在通过 5 个可自定义的步骤为你提供高效的工作流程,并在文末提供我的远程可执行脚本。 让我们开始吧!
1、搭建环境
在上一篇文章中,我们了解了如何使用 Anaconda 轻松设置环境,以及如何使用 GUI Spyder 来管理代码。 我们将继续这种方式,只使用 2 个库。
为了从点云中自动获取 3D 网格,我们将在我们的环境中添加另一个库 Open3D。 它是一个开源库,允许使用一组高效的数据结构和算法进行 3D 数据处理。 安装需要单击环境旁边的 ▶️ 图标。
打开终端并运行以下命令:
conda install -c open3d-admin open3d==0.8.0.0
🤓 注意:Open3D包兼容python 2.7、3.5和3.6版本。 如果你有另一个,你可以创建一个新环境(最好),或者如果你从上一篇文章开始,通过在终端中输入 conda install python=3.5 来更改终端中的 python 版本。
这将自动安装包及其依赖项,你可以在终端提示时输入 y 以允许此过程。 现在已经为项目做好了准备。
2、加载并准备数据
启动你的 python 脚本工具(Spyder GUI、Jupyter 或 Google Colab),我们将在其中调用 2 个库:Numpy 和 Open3D。
import numpy as np
import open3d as o3d
然后,我们创建保存数据路径和点云数据的变量:
input_path="your_path_to_file/"
output_path="your_path_to_output_folder/"
dataname="sample.xyz"
point_cloud= np.loadtxt(input_path+dataname,skiprows=1)
🤓 注意:至于上一篇文章,我们将使用采样点云,你可以从该存储库免费下载。 如果你想在不安装任何东西的情况下预先可视化它,你可以查看 webGL 版本。
最后,我们将 point_cloud 变量类型从 Numpy 转换为 Open3D o3d.geometry.PointCloud 类型以进行进一步处理:
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(point_cloud[:,:3])
pcd.colors = o3d.utility.Vector3dVector(point_cloud[:,3:6]/255)
pcd.normals = o3d.utility.Vector3dVector(point_cloud[:,6:9])
🤓 注意:以下命令首先实例化Open3d点云对象,然后从原始NumPy数组中添加点、颜色和法线。
要快速查看加载的内容,可以执行以下命令(在 Google Colab 中不起作用):
o3d.visualization.draw_geometries([pcd])
3、选择网格生成策略
现在我们准备好通过对 pcd 点云进行网格化来开始表面重建过程。 我将给出我最喜欢的有效获取结果的方法,但在我们深入研究之前,需要一些浓缩的细节来掌握底层过程。 我将限制自己使用两种网格生成策略。
策略一:球旋转算法
球旋转算法 (BPA:Ball-Pivoting Algorithm) 背后的想法是模拟使用虚拟球从点云生成网格。 我们首先假设给定的点云由从物体表面采样的点组成。 点必须严格代表一个表面(无噪声),即重建的网格。
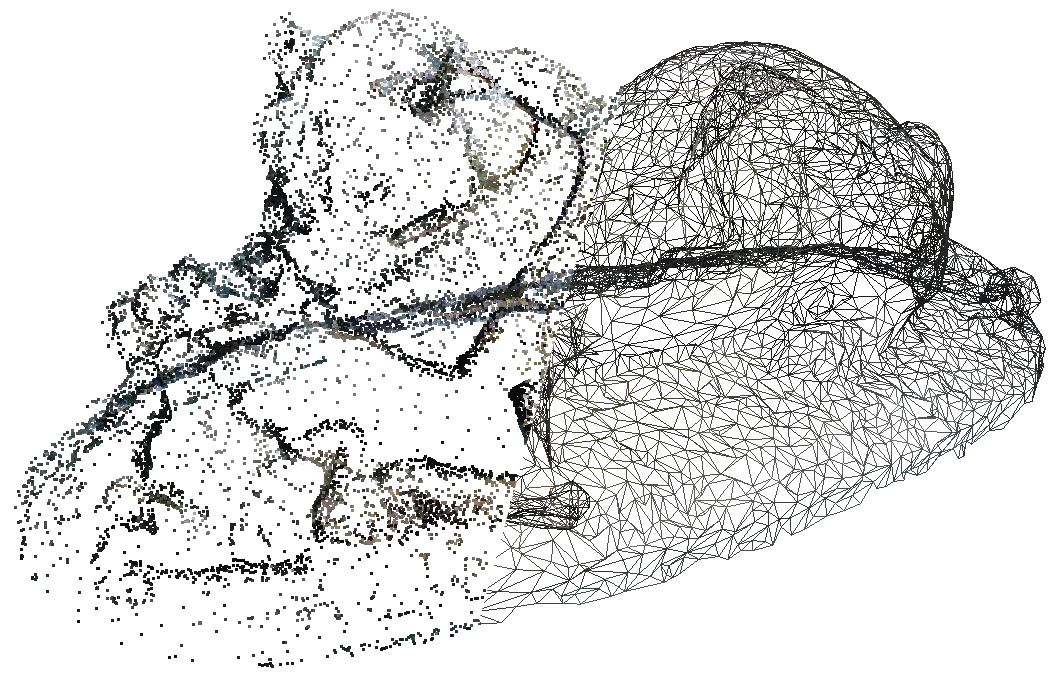
基于这个假设,想象一下在点云“表面”上滚动一个小球。 这个小球取决于网格的比例,应该略大于点之间的平均间距。 当你将球放到点的表面上时,球将被抓住并落在将形成种子三角形的三个点上。 从那个位置开始,球沿着由两点形成的三角形边滚动。 然后球落在一个新的位置:一个新的三角形由两个先前的顶点组成,一个新的三角形被添加到网格中。 当我们继续滚动和旋转球时,会形成新的三角形并将其添加到网格中。 球继续滚动和滚动,直到网格完全形成。
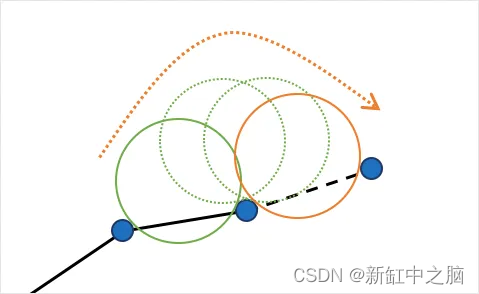
Ball-Pivoting Algorithm 背后的想法很简单,但当然,这里最初表达的过程有很多注意事项:
- 球半径如何选择? 半径是根据输入点云的大小和比例凭经验获得的。 理论上,球的直径应该略大于点间的平均距离。
- 如果某些位置的点相距太远并且球掉落怎么办? 当球沿边缘旋转时,它可能会错过表面上的适当点,而是击中物体上的另一个点,甚至正好是它的三个旧点。 在这种情况下,我们检查新三角形 Facet 的法线是否与点的 Vertex 法线一致。 如果不是,那么我们拒绝那个三角形并创建一个洞。
- 如果表面有折痕或凹陷,使得表面与自身之间的距离小于球的大小怎么办? 在这种情况下,球只会滚过折痕而忽略折痕内的点。 但是,这不是理想的行为,因为重建的网格对对象不准确。
- 如果表面被分隔成点区域,以至于球无法在区域之间成功滚动怎么办? 虚拟球在不同位置多次落到表面上。 这可确保球捕获整个网格,即使点的间距不一致也是如此。
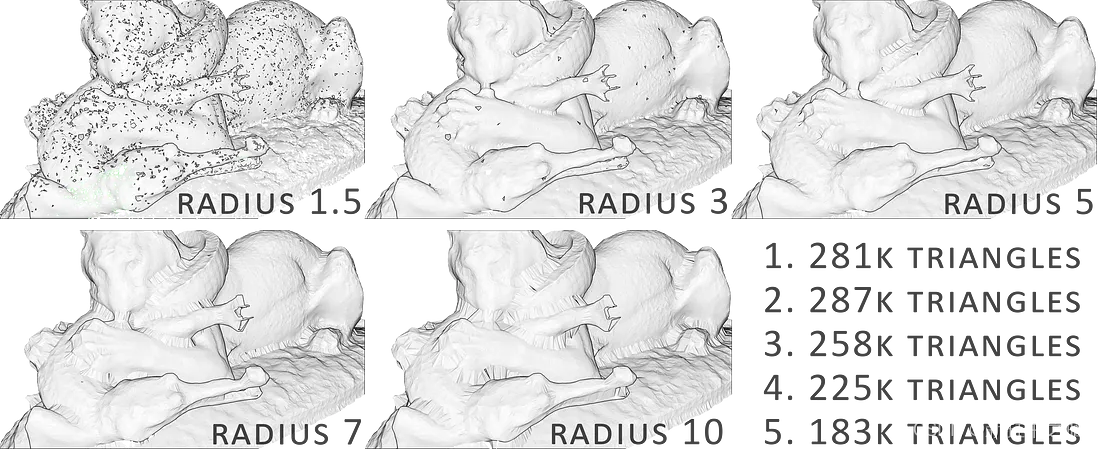
策略二:泊松重建
泊松重建更具技术/数学意义。 它的方法被称为隐式网格划分方法,我将其描述为试图将数据“包裹”在光滑的布料中。 在不涉及太多细节的情况下,我们尝试通过创建一个代表与法线链接的等值面的全新点集来从原始点集拟合水密表面。 有几个参数可以影响网格划分的结果:
-
怎么设置深度? 树深度用于重建。 网格越高越详细(默认值:8)。 对于嘈杂的数据,你在生成的网格中保留异常值的顶点,但算法不会检测到它们。 所以较低的值(可能在 5 到 7 之间)提供平滑效果,但您会丢失细节。 深度值越高,生成的网格的顶点数量就越高。
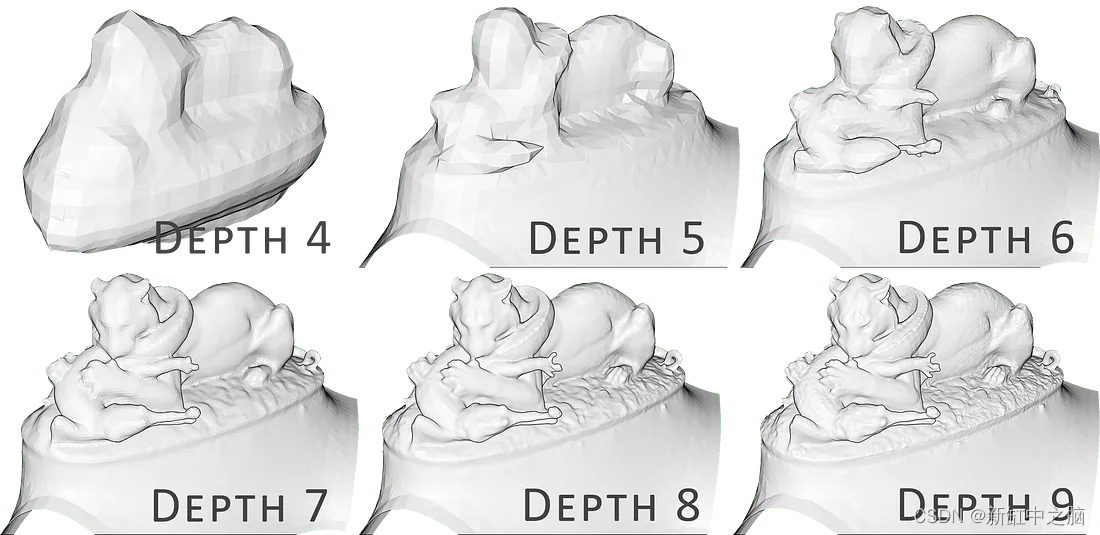
-
怎么设置宽度? 这指定了树结构最细级别的目标宽度,称为八叉树🤯。 别担心,我将在另一篇文章中介绍这个和 3D 的最佳数据结构,因为它扩展了本文的范围。 无论如何,如果指定了深度,则忽略此参数。
-
怎么设置缩放比例? 它描述了用于重建的立方体的直径与样本边界立方体的直径之间的比率。 非常抽象,默认参数通常效果很好(1.1)。

-
使用哪种拟合算法? linear_fit 参数如果设置为 true,让重建器使用线性插值来估计等顶点的位置。
4、处理数据
策略 1:BPA
我们首先根据从所有点之间的距离计算出的平均距离来计算必要的半径参数:
distances = pcd.compute_nearest_neighbor_distance()
avg_dist = np.mean(distances)
radius = 3 * avg_dist
在一个命令行中,我们可以创建一个网格并将其存储在 bpa_mesh 变量中:
bpa_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(pcd,o3d.utility.DoubleVector([radius, radius * 2]))
在导出网格之前,我们可以将结果下采样到可接受的三角形数量,例如 100k 个三角形:
dec_mesh = mesh.simplify_quadric_decimation(100000)
此外,如果你认为网格会出现一些奇怪的伪影,可以运行以下命令来确保其一致性:
dec_mesh.remove_degenerate_triangles()
dec_mesh.remove_duplicated_triangles()
dec_mesh.remove_duplicated_vertices()
dec_mesh.remove_non_manifold_edges()
策略 2:泊松重建
🤓 注意:该策略从Open3D 0.9.0.0版本开始可用,因此目前只能远程使用。 你可以通过我在此处提供的 google colab 代码执行它。
要获得泊松结果,非常简单。 只需调整传递给函数的参数,如上所述:
poisson_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(pcd, depth=8, width=0, scale=1.1, linear_fit=False)[0]
🤓 注意:该函数输出一个列表,该列表由一个 o3d.geometry 对象和一个 Numpy 数组组成。 你只需要选择最后证明 [0] 的 o3d.geometry。
为了获得干净的结果,通常需要添加一个裁剪步骤来清除下图中以黄色突出显示的不需要的伪影:
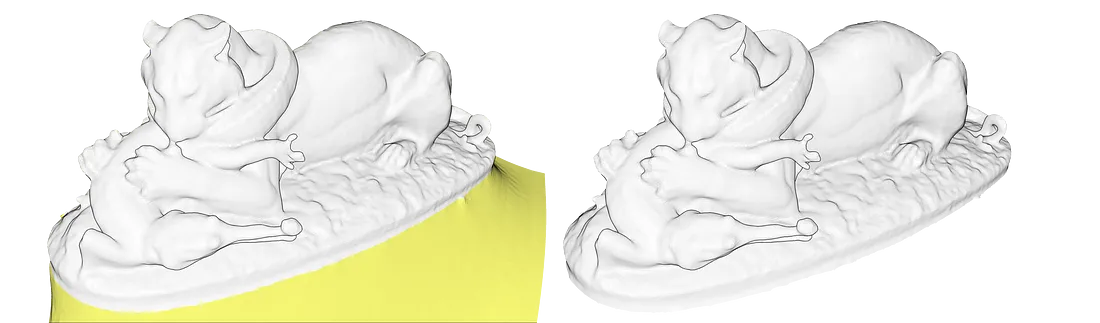
为此,我们计算包含原始点云的初始边界框,并使用它从边界框外的网格中过滤所有表面:
bbox = pcd.get_axis_aligned_bounding_box()
p_mesh_crop = poisson_mesh.crop(bbox)
你现在拥有一个或多个变量,每个变量都包含网格几何体! 在应用程序中获取它的最后一步是导出它!
5、导出和可视化
使用 write_triangle_mesh 函数导出网格数据非常简单。 我们只需在创建文件的名称中指定我们想要的 .ply、.obj、.stl 或 .gltf 扩展名,以及要导出的网格。 下面,我们将 BPA 和泊松重建导出为 .ply 文件:
o3d.io.write_triangle_mesh(output_path+"bpa_mesh.ply", dec_mesh)
o3d.io.write_triangle_mesh(output_path+"p_mesh_c.ply", p_mesh_crop)
为了快速生成细节层次 (LoD),让我们编写第一个函数。 这将非常简单。 该函数将采用网格、LoD 列表(作为三角形的目标数量)、生成文件的文件格式和写入文件的路径作为参数。 该函数(写在脚本中)如下所示:
def lod_mesh_export(mesh, lods, extension, path):mesh_lods={}for i in lods:mesh_lod = mesh.simplify_quadric_decimation(i)o3d.io.write_triangle_mesh(path+"lod_"+str(i)+extension, mesh_lod)mesh_lods[i]=mesh_lodprint("generation of "+str(i)+" LoD successful")return mesh_lods
💡 提示:我将在另一篇文章中介绍该函数的作用及其结构的基础知识。 此时,知道该函数将 (1) 以所需文件格式将数据导出到您选择的指定位置,以及 (2) 如果需要更多处理,则可以将结果存储在变量中,这很有用 在 python 中需要。
该函数具有一些魔力,但一旦执行,它看起来什么也没有发生。 不用担心,你的程序现在知道 lod_mesh_export 是什么,可以直接在控制台中调用它,我们只需将参数更改为所需的值即可:
my_lods = lod_mesh_export(bpa_mesh, [100000,50000,10000,1000,100], ".ply", output_path)
非常有趣的是,现在不需要为不同的 LoD 每次都重写一堆代码。 只需要将不同的参数传递给函数:
my_lods2 = lod_mesh_export(bpa_mesh, [8000,800,300], ".ply", output_path)
如果你想在 python 中可视化一个特定的 LoD,比如说有 100 个三角形的 LoD,你可以通过以下命令访问和可视化它:
o3d.visualization.draw_geometries([my_lods[100]])
要在 python 之外进行可视化,可以使用选择的软件(例如开源 Blender、MeshLab 和 CloudCompare)并在 GUI 中加载导出的文件。 通过 WebGL 直接在 Web 上,也可以使用 Three.js 编辑器或 Flyvast 来简单地访问网格。
最后,可以在任何 3D 打印软件中导入它,并通过在线打印服务获得关于它需要多少费用的报价🤑。

6、错误的法线
在这个指南中,我们介绍了如何从点云设置自动 Python 3D 网格创建器。 这是一个非常好的工具,将在许多 3D 自动化项目中证明非常方便! 然而,我们假设点云已经没有噪声,并且法线方向正确。

如果法线有问题,则需要一些额外的步骤,我们将在另一篇文章中介绍如何处理。
完整代码可在此处访问:Google Colab notebook 。
7、结束语
我们刚刚学习了如何导入、划分网格、导出和可视化由数百万个具有不同 LoD 的点组成的点云! 做得好! 但路径并没有就此结束,未来的帖子将深入探讨点云空间分析、文件格式、数据结构、可视化、动画和网格划分。 我们将特别研究如何管理下文定义的大点云数据。
原文链接:点云转3D网格 — BimAnt
相关文章:

点云转3D网格【Python】
推荐:使用 NSDT场景设计器 快速搭建 3D场景。 在本文中,我将介绍我的 3D 表面重建过程,以便使用 Python 从点云快速创建网格。 你将能够导出、可视化结果并将结果集成到您最喜欢的 3D 软件中,而无需任何编码经验。 此外࿰…...
【OpenCV图像处理系列一】OpenCV开发环境的安装与搭建(Ubuntu + Window都适用)
🔗 运行环境:OpenCV,Ubuntu,Windows 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### &#x…...

【代码随想录】-动态规划专题
文章目录理论基础斐波拉契数列爬楼梯使用最小花费爬楼梯不同路径不同路径 II整数拆分不同的二叉搜索树背包问题——理论基础01背包二维dp数组01背包一维数组(滚动数组)装满背包分割等和子集最后一块石头的重量 II目标和一和零完全背包零钱兑换 II组合总和…...

c++数据类型 输入输出
C++语法 //常用包: iostream:cin cout endl cstdio:scanf printf algorithm:max min reverse swap cstring:memset memcpymemset(a,-1,sizeof a) 填充数组memcpy(b,a,sizeof a) 将a数组复制到b数组,长度是a数组字节长度 cmath:sin sqrt pow abs fabs编程是一种控制计…...
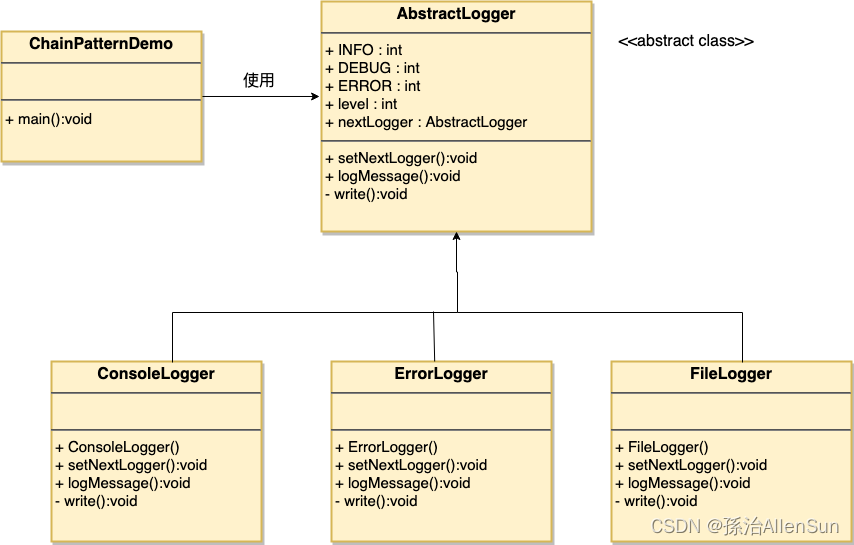
【设计模式-11】责任链模式
认识设计模式(十一)---责任链模式【一】责任链模式【二】介绍(1)意图(2)主要解决(3)何时使用(4)如何解决(5)关键代码(6&am…...
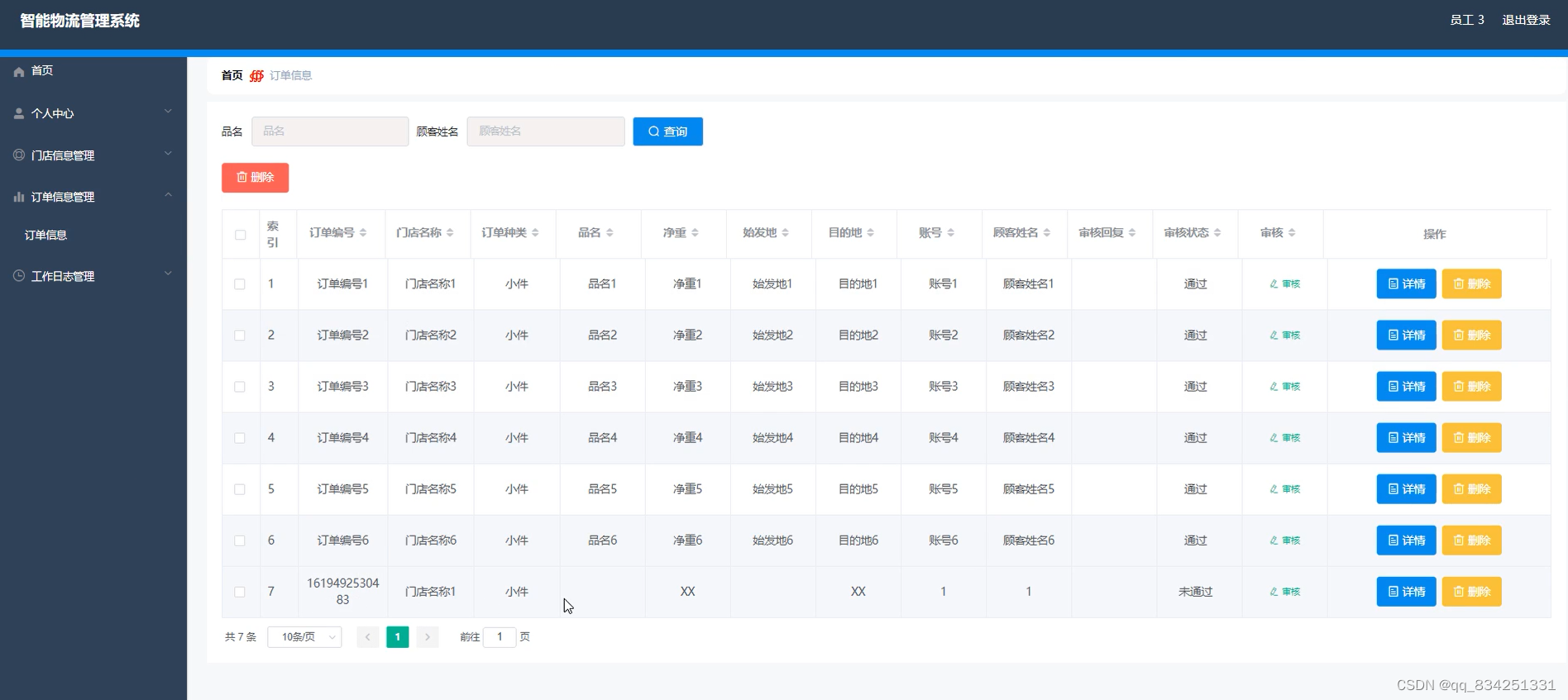
SpringBoot+Vue实现智能物流管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

【MT7628】MT7628如何修改串口波特率、调试串口物理口、使用UART3口
环境说明 sdk版本:Mediatek_ApSoC_SDK_4320_20150414.tar.bz2 芯片方案:MT7628A Uboot修改串口波特率方法 修改rt2880.h文件 修改include/configs/rt2880.h文件CONFIG_BAUDRATE宏的值 - #define CONFIG_BAUDRATE 57600 +#define CONFIG_BAUDRATE 115200 Kernel中修改串口波特…...

css盒模型介绍
在使用CSS进行网页布局时,我们一定离不开的一个东西————盒子模型。盒子模型,顾名思义,盒子就是用来装东西的,它装的东西就是HTML元素的内容。或者说,每一个可见的 HTML 元素都是一个盒子,下面所说的盒子…...

onetab 谷歌插件历史数据清除
文章目录方法1:测试也可以步骤1:批量执行点击步骤2:python 脚本模拟点击确定操作方法2:成功【推荐】步骤1:修改confirm,类似于hook操作步骤2:批量点击删除操作:onetab 谷歌插件历史数…...

GRBL源码简单分析
结构体说明 GRBL里面的速度规划是带运动段前瞻的,所以有规划运动段数据和微小运动段的区分 这里的“规划运动段”对应的数据结构是plan_block_t,前瞻和加减速会使用到,也就是通过解析G代码后出来的直接直线数据或是圆弧插补出来的拟合直线数据…...
)
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(谓语动词的情态)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

软考高级考试中有五大证书,其中哪个更值得考?
计算机软考属于专业技术人员职业资格水平评价类,是职业资格、专业技术资格(职称)和专业技术水平"三合一"的考试,是目前IT行业仅有的国家级考试。考试不受学历、专业、资历等条件限制。软考高级考试中有五大证书…...

FlexRay™ 协议控制器 (E-Ray)-04
网络管理 累积的网络管理 (NM) 向量位于网络管理寄存器 1 到网络管理寄存器 3 (NMVx (x = 1-3)) 中。【The accrued Network Management (NM) vector is located in the Network Management Register 1 to Network Management Register 3 (NMVx (x = 1-3)).】 网络管理向量 x…...

container_of 根据成员变量获得包含其的对象的地址!
写在前面 本系列文章的灵感出处均是各个技术书籍的读后感,详细书籍信息见文章最后的参考文献 CONTAINER_OF 在书中发现一个很有意思的宏,以此可以衍生出来其很多的用法,这个宏可以根据某个成员变量的地址得到包含这个成员变量地址的对象的…...
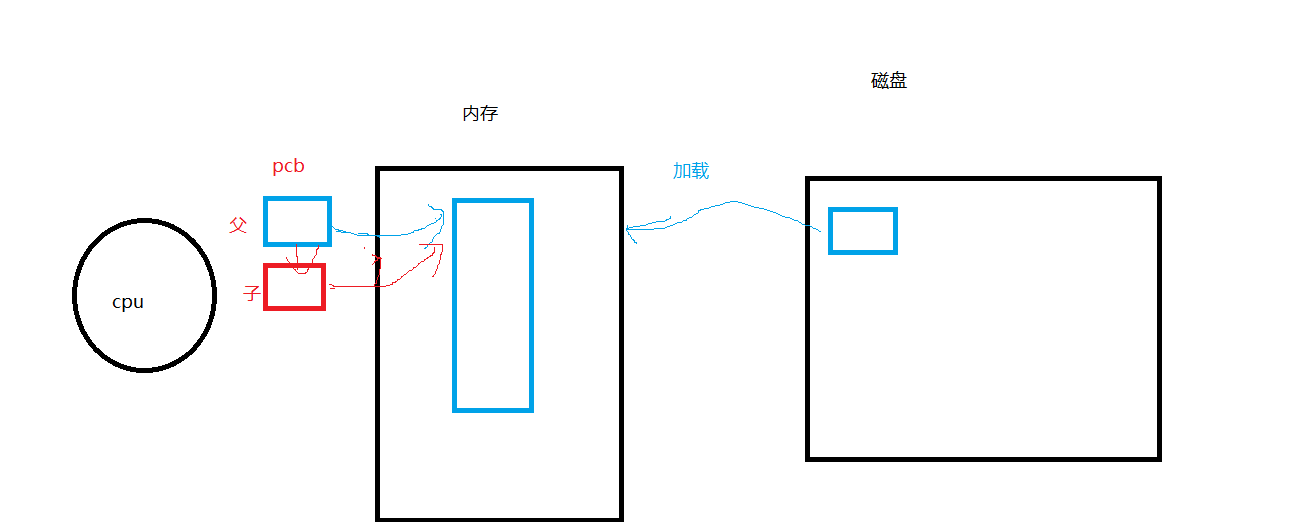
Linux进程概念
Linux进程概念前言冯诺依曼体系操作系统设计操作系统的目的如何理解OS是一款搞“管理”的软件?系统调用和库函数的概念进程的概念描述进程组织进程查看进程fork()前言 本篇博客主要介绍一些:冯诺依曼体系、OS的理解、进程的一些概…...
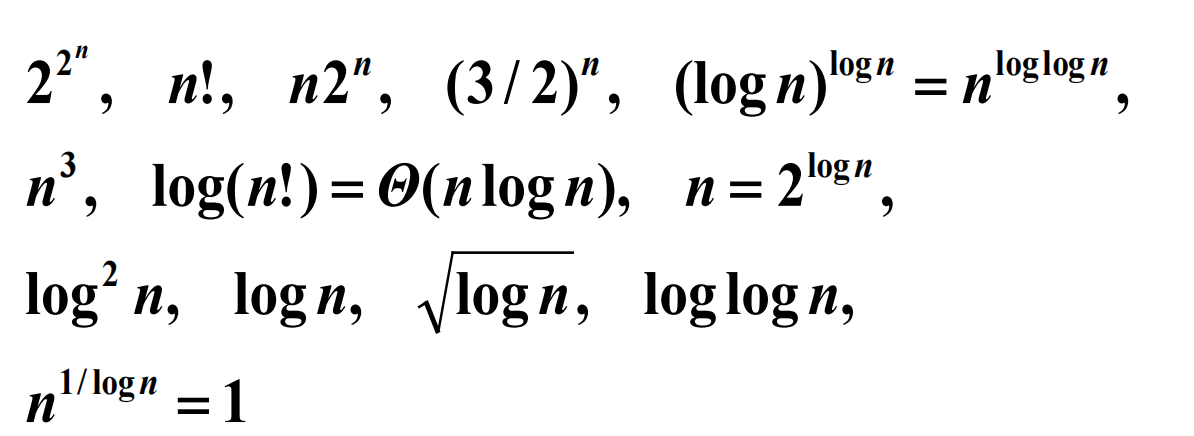
算法设计与分析
两个例子:调度问题与投资问题 例1:调度问题 问题 有 n 项任务,每项任务加工时间已知.从 0时刻开始陆续安排到一台机器上加工. 每个任务的完成时间是从 0 时刻到任务加工截止的时间. 求: 总完成时间(所有任务完成时间之和)最短…...
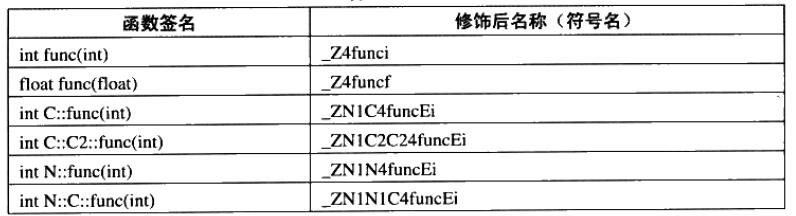
C++ 基础
命名空间 在 C/C 中,变量、函数和类都是大量存在的,这些变量、函数和类的名称将都存在全局作用域中,可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化,以避免命名冲突或名字污染,namespace 关键字的…...
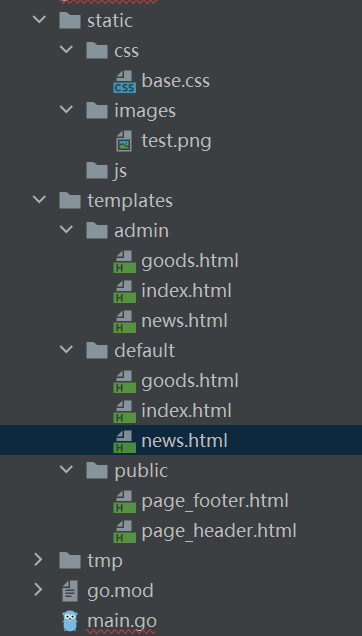
[golang gin框架] 2.Gin HTML模板渲染以及模板语法,自定义模板函数,静态文件服务
一.Gin HTML 模板渲染全部模板放在一个目录里面的配置方法首先在项目根目录新建 templates 文件夹,然后在文件夹中新建 对应的index.html<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta http…...
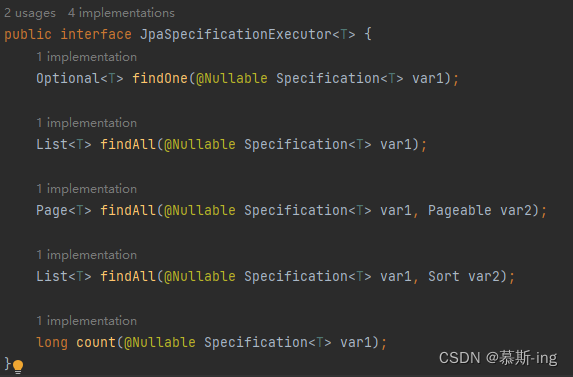
数据仓库层Repository(CrudRepository、PagingAndSortingRepository、JpaRepository)
什么是数据仓库层Repository? 数据仓库接口的作用:Repository原意指的是仓库,即数据仓库的意思。Repository居于业务层和数据层之间,将两者隔离开来,在它的内部封装了数据查询和存储的逻辑。 Repository接口ÿ…...
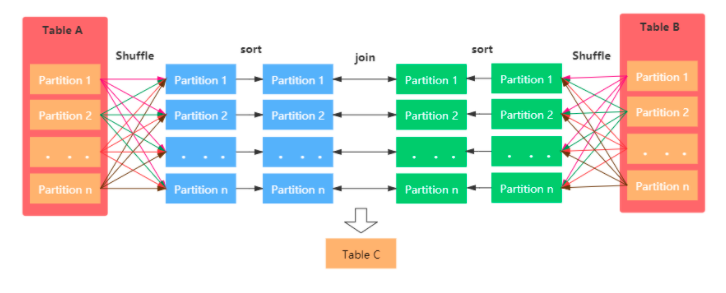
大数据技术架构(组件)33——Spark:Spark SQL--Join Type
2.2.2、Join Type2.2.2.1、Broadcast Hash Join (Not Shuffled)就是常说的MapJoin,join操作在map端进行的。场景:join的其中一张表要很小,可以放到Driver或者Executor端的内存中。原理:1、将小表的数据广播到所有的Executor端,利用collect算子…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
