三次样条样条:Bézier样条和Hermite样条
总结 What is the Difference Between Natural Cubic Spline, Hermite Spline, Bézier Spline and B-spline?
1.多项式拟合中的 Runge Phenomenon
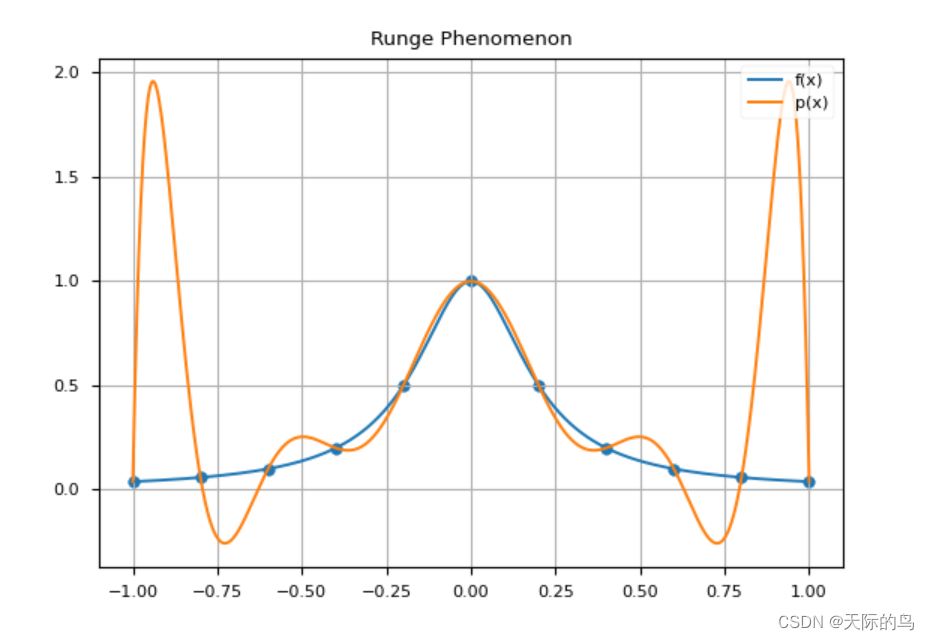
找到一条通过N+1个点的多项式曲线 ,需要N次曲线。通过两个点的多项式曲线为一次,三个点的多项式曲线为二次。当点数较多时,曲线阶数增高,在端点处易出现 Runge Phenomenon。这种现象是指,在曲线阶数较高时,拟合的结果可能在端点处与实际产生很大的误差。比如下图中,蓝色曲线是实际曲线,橙色是对11个点拟合产生得到10次多项式,在端点处发生了很大的抖动。
2.Bernstein Polynomials(伯恩斯坦多项式)and Bézier Curves(贝塞尔曲线)
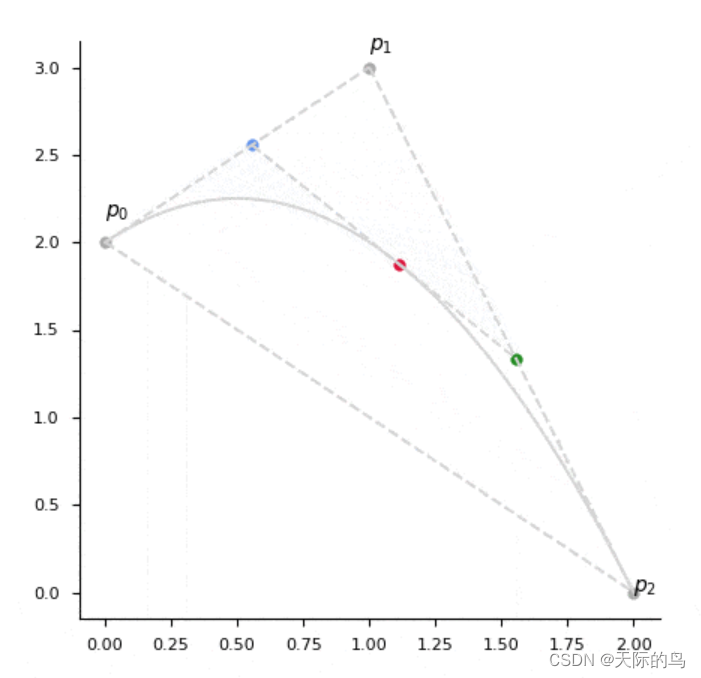
伯恩斯坦多项式的图解:下图中,黄蓝色点从P0往P1匀速前进,在0时刻位于P0,在1时刻位于P1;类似地绿色点从P1匀速朝着P2前进,那么蓝点和绿点就是一条位置和长度都动态变化的线段。在这个前提下,红色点沿着动态的蓝绿线段“匀速”前进,“匀速”的含义是蓝红线段长度除以蓝绿线段的长度的值,等于时间t,即这个值在0时刻等于0,在1时刻等于1。
 根据上边的情况,可以推导出红点的位置与时间t的关系为下图。可以得出,红点的位置,是P0,P1,P2的一个组合。红点的位置曲线随着三个控制点P0P1P2的变化而唯一确定。
根据上边的情况,可以推导出红点的位置与时间t的关系为下图。可以得出,红点的位置,是P0,P1,P2的一个组合。红点的位置曲线随着三个控制点P0P1P2的变化而唯一确定。
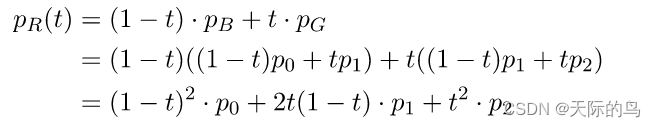
三个控制点前的系数叫做Bernstein basis polynomials,红点的位置曲线叫做二次贝塞尔曲线。可以注意到,二次贝塞尔曲线的三个控制点中,有两个在曲线上,作为曲线的起点和终点,一般是固定的。那么曲线就由第三个控制点唯一确定,在Bezier tool上通过拖动这个控制点,可以方便地获得自己想要的二次贝塞尔曲线。
伯恩斯坦二次多项式基底,注意这个基地是可以扩展到更高次的,详见bezier + spline。即对于三个控制点可以用二次贝萨尔曲线拟合,四个控制点可以用三次拟合,以此类推。高阶的贝萨尔曲线可能会比较复杂,使用分段贝萨尔曲线就可以得到B-样条。具体参考贝萨尔曲线和B样条

3.Hermite Basis Polynomials and Cubic Hermite Interpolation
Hermite曲线:考虑一个关于时间t的三次多项式 p(t) = at^3 + bt^2 + ct + d,他有四个未知数,那么找到找到四个等式,那么就能解析出四个未知数。首尾端点可以构造出两个等式,Hermite曲线假设首尾端点处的斜率也是已知的,那么就有四个不相关的条件构造出四个等式,唯一地解出多项式。
Hermite多项式的**四个条件**

解析出的Hermite三次多项式
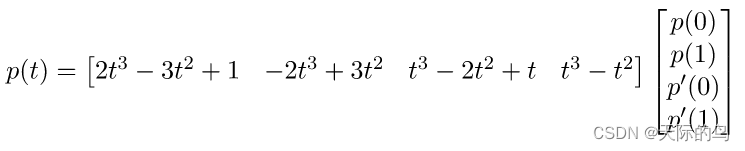
注意Hermite曲线与贝塞尔曲线有一个共同点 :首尾端点固定的情况下,利用某些额外的条件,寻找一条平滑的曲线。
4.三次样条
样条函数是使用最多的分段多项式插值方法,k次样条由多段k次多项式曲线组成。一个k次样条,除了函数值连续,在曲线区间内,也是k-1次可微(k-2次导数连续),并且k-1次导数连续。使用最多的是三次样条,相较于一次和二次样条,它具有平滑和变化的二阶导数,具有更多的变换性质。

自然样条:得到的曲线通过所有的节点,一个控制点位置的改变,会影响其他段的曲线,是非local的
B-spline:得到的曲线是节点的加权平均,不保证通过节点,是一种拟合,能保证二阶导连续 。且优点是移动一个控制点,其他点不一定会变化
贝塞尔曲线:由控制点确定,通过起点和终点,能保证一阶导连续
分段Hermite:给定每一段曲线起点和终点的一阶导数,就可以确定曲线,可以控制一阶导数连续。
###6. 个人总结
三次样条:得到的曲线通过每一个节点,一阶导二阶导都连续,不过当一个节点发生变化时,整个曲线需要重新计算。
B-样条:把节点认为是控制点,曲线不一定经过节点,是一个近似的拟合。优点是,可以单独改变某一段曲线,而不影响其他段。
相关文章:

三次样条样条:Bézier样条和Hermite样条
总结 What is the Difference Between Natural Cubic Spline, Hermite Spline, Bzier Spline and B-spline? 1.多项式拟合中的 Runge Phenomenon 找到一条通过N1个点的多项式曲线 ,需要N次曲线。通过两个点的多项式曲线为一次,三个点的多项式曲线为二…...
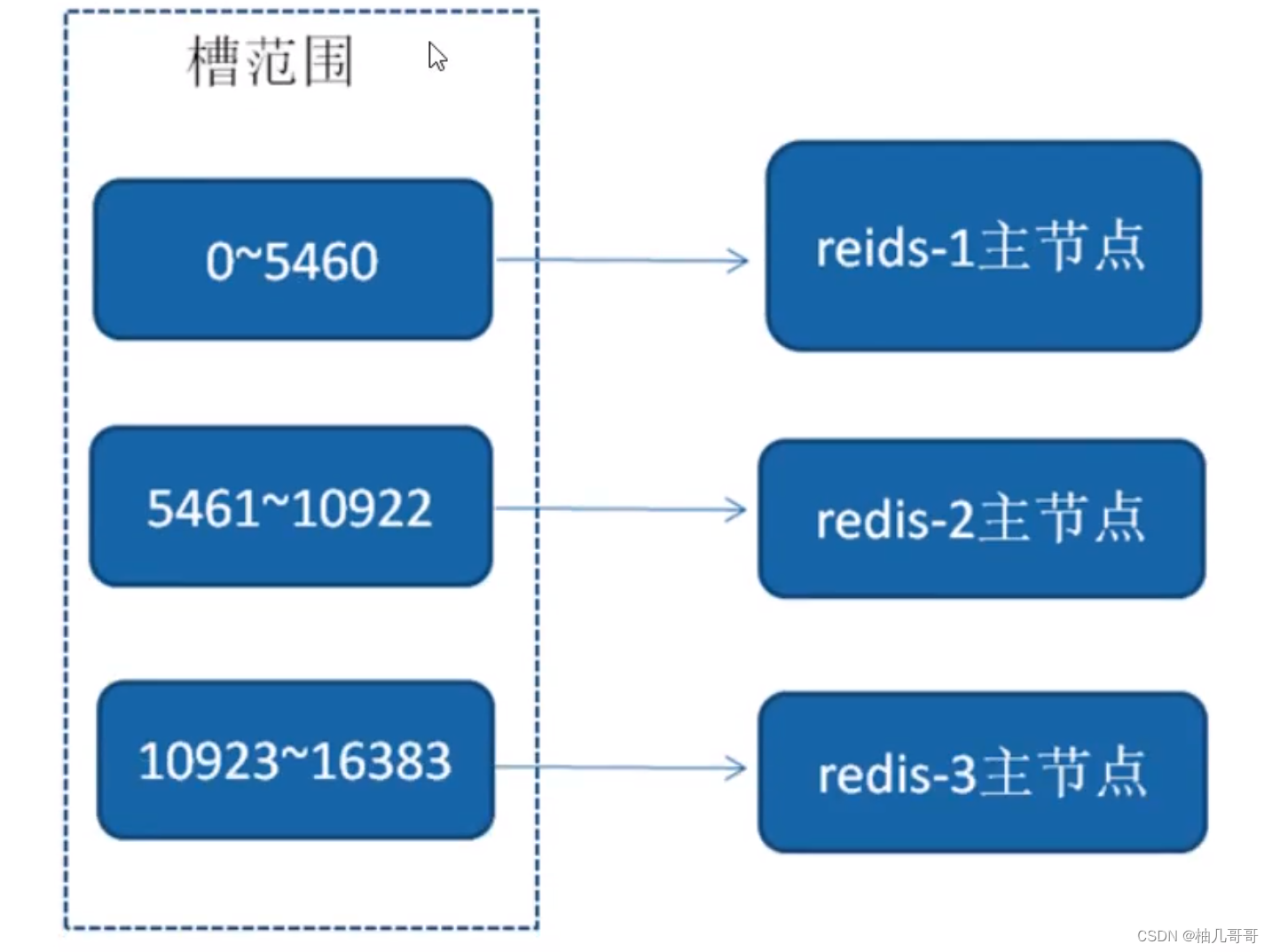
Redis面试题 (2023最新版)
文章目录一、Redis为什么快?1、纯内存访问2、单线程,避免上下文切换3、渐进式ReHash、缓存时间戳(1)渐进式ReHash:(2)缓存时间戳:二、Redis合适的应用场景常用基本数据类型ÿ…...

基于springboot实现家乡特色食品景点推荐系统【源码+论文】分享
基于springboot实现家乡特色推荐系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&…...
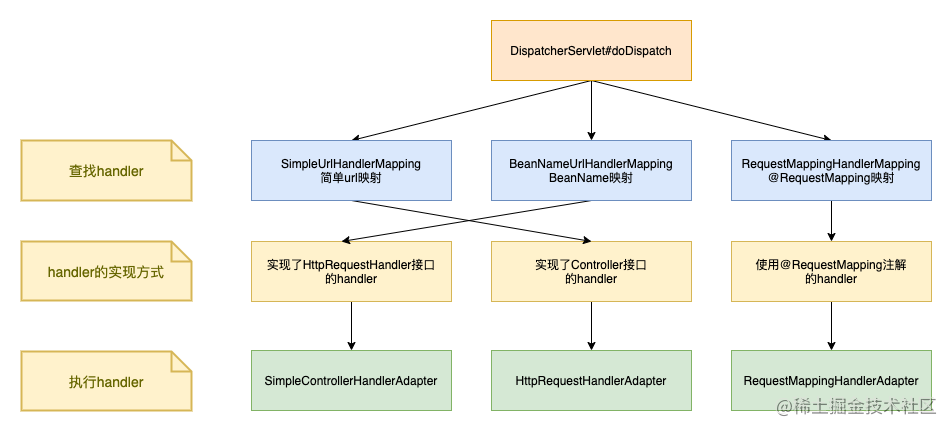
Spring MVC 启动之 HandlerMapping
在上一篇文章中,我们介绍了 Spring MVC 的启动流程,接下来我们将发分多个篇章详细介绍流程中的重点步骤 今天我们从 HandlerMapping 开始分析,HandlerMapping 是框架中的一个非常重要的组件。它的作用是将URL请求映射到合适的处理程序&#x…...

基于YOLOv5的停车位检测系统(清新UI+深度学习+训练数据集)
摘要:基于YOLOv5的停车位检测系统用于露天停车场车位检测,应用深度学习技术检测停车位是否占用,以辅助停车场对车位进行智能化管理。在介绍算法原理的同时,给出Python的实现代码、训练数据集以及PyQt的UI界面。博文提供了完整的Py…...

【Linux系统编程】5.vim基本操作命令
目录 跳转到指定行 命令模式 末行模式 跳转行首 跳转行尾 自动格式化代码 大括号、中括号、小括号对应 光标移至行首 光标移至行尾 删除单个字符 删除一个单词 删除光标至行尾 删除光标至行首 替换单个字符 删除指定区域 删除指定1行 删除指定多行 复制一行 …...
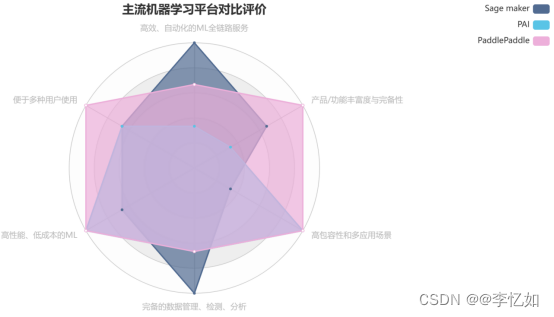
主流机器学习平台调研与对比分析
梗概 本报告主要调研目前主流的机器学习平台,包括但不限于Amazon的Sage maker,Alibaba的PAI,Baidu的PaddlePaddle。对产品的定位、功能、实践、定价四个方面进行详细解析,并通过标杆对比分析提出一套机器学习平台评价体系&#x…...

作业帮基于明道云开展的硬件业务数字化建设
今天由我代表作业帮来介绍公司在低代码平台应用的一些经验和心得。我今天分享的内容包含两部分,一个是作业帮硬件的介绍,另一个是基于明道云的系统能力建设,也是我们自己总结的经验,希望能给大家带来一些启发。 一、关于作业帮 …...

位图及布隆过滤器的模拟实现与面试题
位图 模拟实现 namespace yyq {template<size_t N>class bitset{public:bitset(){_bits.resize(N / 8 1, 0);//_bits.resize((N >> 3) 1, 0);}void set(size_t x)//将某位做标记{size_t i x / 8; //第几个char对象size_t j x % 8; //这个char对象的第几个比特…...

在 Python 中将天数添加到日期
使用 datetime 模块中的 timedelta() 方法将天数添加到日期中,例如 result_1 date_1 timedelta(days3)。 timedelta 方法可以传递天数参数并将指定的天数添加到日期。 from datetime import datetime, date, timedelta# ✅ 将天数添加到日期 my_str 09-24-2023 …...

vue3知识点
一、vue3带来了什么? 1.性能的提升 打包大小减少41% 初次渲染快55%,更新渲染快133% 内存减少54% 2.源码的升级 使用Proxy代替defineProperty实现响应式 重写虚拟DOM的实现和Tree-shaking 3.拥抱TypeScript Vue3可以更好的支持TypeScript 4.新的特性 4.1.…...
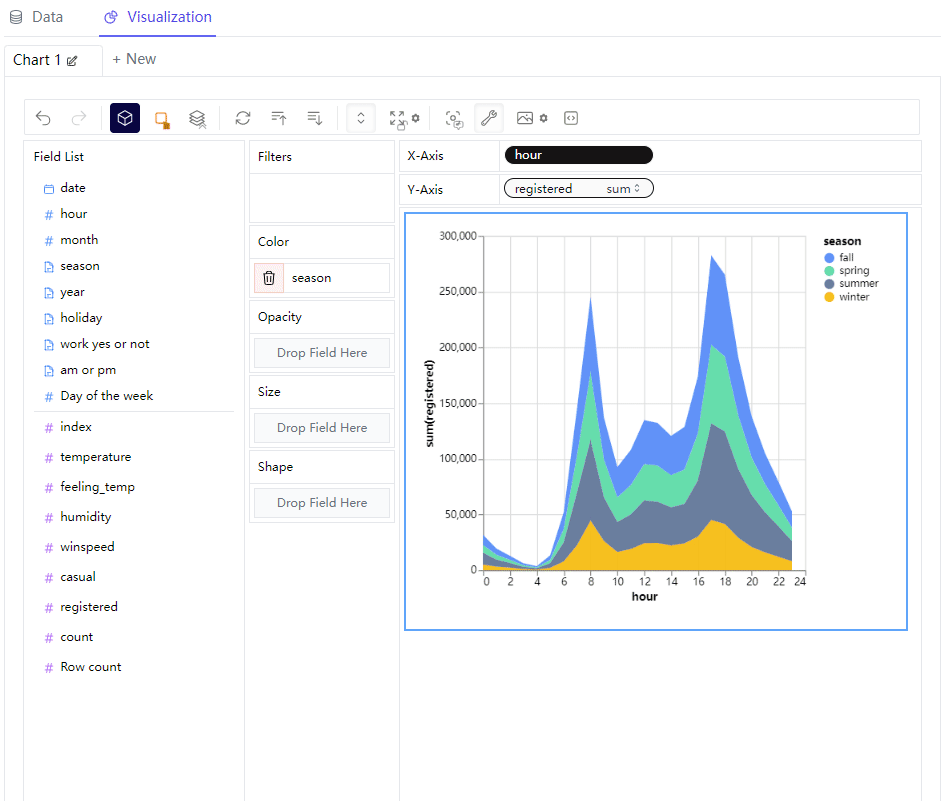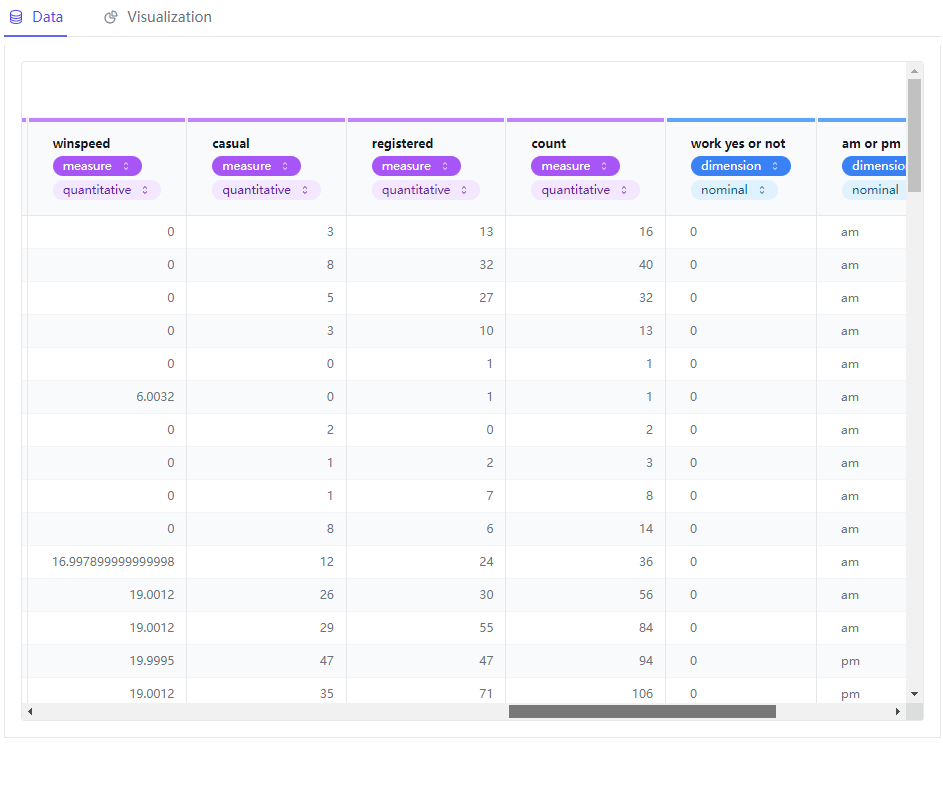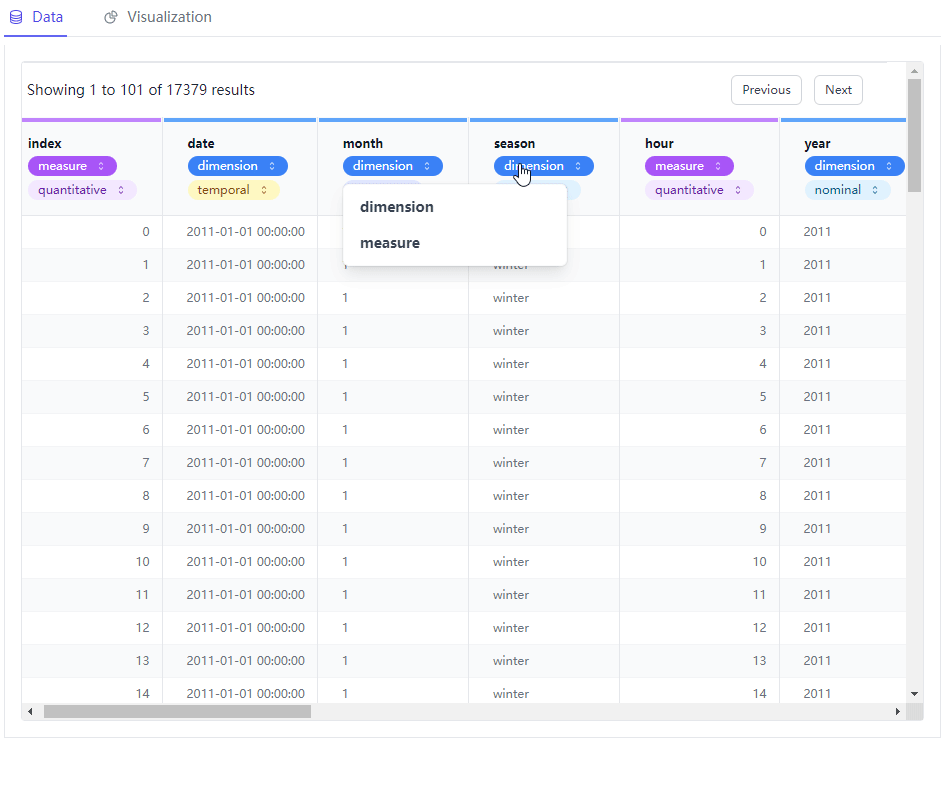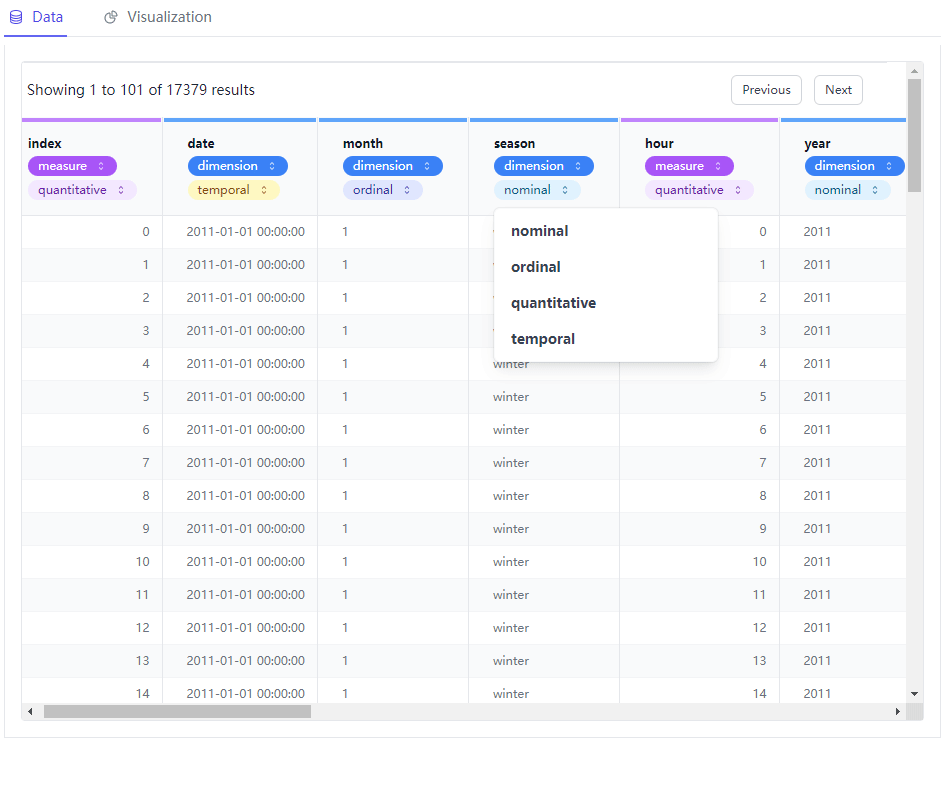
一行代码生成Tableau可视化图表
今天给大家介绍一个十分好用的Python模块,用来给数据集做一个初步的探索性数据分析(EDA),有着类似Tableau的可视化界面,我们通过对于字段的拖拽就可以实现想要的可视化图表,使用起来十分的简单且容易上手,学习成本低&a…...
)
链表——删除元素或插入元素(头插法及尾插法)
目录 链表的结点由一个结构体构成 判断链表是否为空 键盘输入链表中的数据 输出链表中的数据 返回链表的元素个数 清空链表 返回指定位置的元素值 查找数据所在位置 删除链表的元素 插入元素 建立无头结点的单链表 建立有头结点的单链表(头插法ÿ…...

oracle容器的使用
oracle容器的使用 1.下载oracle容器 1.1拉取容器 docker pull registry.cn-hangzhou.aliyuncs.com/helowin/oracle_11g拉取国内镜像,该镜像大小为2.99G,已经集成了oracle环境,拉取完可以直接用,推荐使用这款oracle镜像 1.2查看…...

基于springboot会员制医疗预约服务管理信息系统演示【附项目源码】
基于springboot会员制医疗预约服务管理信息系统演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea M…...

GoogleAdsense国内加载慢怎么解决?
一淘模板 56admin.com 发现GoogleAdsense(谷歌广告联盟)国内加载慢拖网站速度怎么解决?GoogleAdsense是谷歌旗下的站长广告联盟系统,如果站长没有好的变现渠道,挂谷歌联盟是最好的选择(日积月累)…...
【MySQL专题】03、性能优化之读写分离(MaxScale)
在我们了解了MySQL的主从复制的性能优化之后,紧接着《【MySQL专题】02、性能优化之主从复制》中,我们提及的读写分离,来进行读操作和写操作分散到不同的服务器结构中,同时希望对多个从服务器能提供负载均衡,读写分离和…...
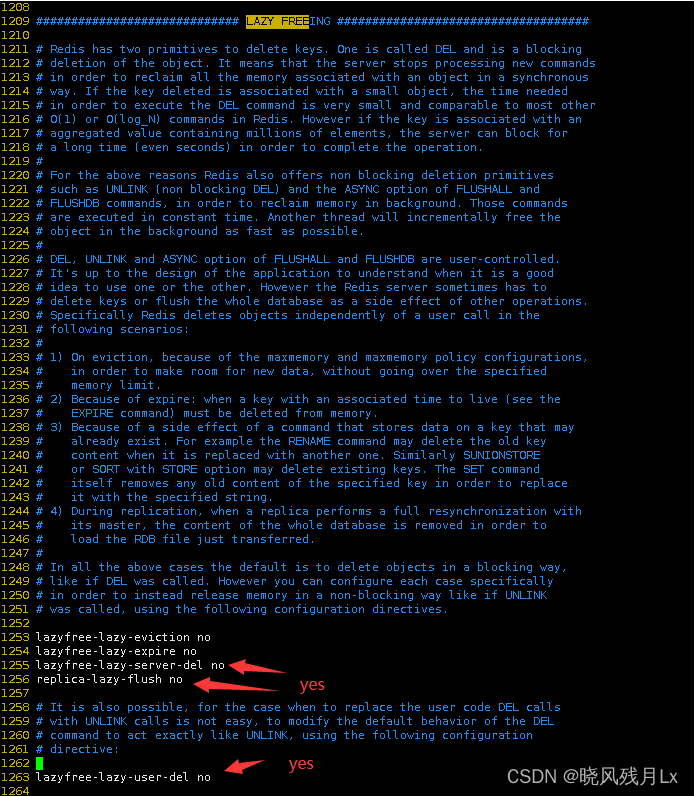
Redis7高级之BigKey(二)
1.MoreKey案例 往redis里面插入大量测试数据key 生成100W条redis批量设置kv的语句保存在redisTest.txt for((i1;i<100*10000;i)); do echo "set k$i v$i" >> /tmp/redisTest.txt ;done; # 生成100W条redis批量设置kv的语句(keykn,valuevn)写入到/tmp目录下的…...

flex弹性盒子
概念 弹性盒子是一种用于按行或者按列布局的一维布局方法,元素可以膨胀以填充额外的空间,缩小以适应更小的空间 以下属性是给父元素添加的 1.flex-direction --改变轴的方向 row 默认值 默认沿着x轴排版(横向从左到右排列(左对齐ÿ…...

[Java Web]Cookie | 一文详细介绍会话跟踪技术中的Cookie
⭐作者介绍:大二本科网络工程专业在读,持续学习Java,努力输出优质文章 ⭐作者主页:逐梦苍穹 ⭐所属专栏:Java Web 目录Cookie1、工作原理2、如何使用2.1、发送Cookie2.2、获取Cookie3、Cookie的存活时间4、中文错误Coo…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
