如何理解Configurational entropy
Configurational entropy 是热力学和统计力学中的一个重要概念,它描述的是系统中由于其微观状态排列(即配置)导致的不确定性或混乱程度。不同于热力学中的热熵(thermal entropy),它特指那些与系统中的粒子、原子、分子或其他单位的排列方式有关的熵。下面详细解释其物理意义、数学表达、应用及相关例子。
1. 物理意义
在统计力学中,熵是系统微观状态数目的量度。每种微观状态是系统中各个组成部分的某种排列或配置。Configurational entropy 是专门描述这些排列可能性的熵,它表示了系统内部结构(如原子、分子、链段等)如何排列的随机性和多样性。
当系统可以有很多种不同的排列方式(即许多可能的微观状态)时,熵会增加。相反,当只有少数排列方式时,熵则较低。
2. 数学表达式
Configurational entropy 通常使用玻尔兹曼熵公式来计算:
其中:
- Sconf是配置熵(configurational entropy)。
- kB是玻尔兹曼常数。
- Ω 是系统的可能微观状态的数量。
这一公式表示,系统的配置熵与系统可以采取的可能配置数的对数成正比。配置越多,系统的熵就越高。
3. 应用与例子
(1)理想气体的混合熵: 在一个理想的气体混合物中,不同种类的气体分子可以随机地分布在整个系统中。如果我们有两种不同的气体混合,它们分子的位置配置就变得复杂。气体分子的不同分布方式代表了不同的微观状态,因此该系统的配置熵会增加。
(2)晶体与无定形材料: 在晶体结构中,原子的排列是非常有序的,几乎没有微观状态的变化可能性,所以配置熵较低。相反,在无定形(非晶态)材料中,原子的排列是无序的,这种无序性导致了更多的可能排列,从而增加了系统的配置熵。
(3)聚合物: 聚合物链中的分子有很多种不同的排列方式和构象(如不同的链折叠、缠绕、拉伸等方式),因此聚合物的配置熵是系统总熵的重要组成部分。例如,对于长链的高分子材料,链段可以自由旋转和扭转,形成许多可能的排列,导致高的配置熵。
(4)化学合金与混合物: 在化学合金中,不同的金属元素可以混合形成不同的排列。例如,在二元合金中,两种不同元素原子在晶格中的排列会导致不同的配置可能性。如果这些原子是随机分布的,则系统的配置熵较高;而如果它们排列得很规则,熵就较低。
4. 配置熵与其他熵的区别
- 热熵(thermal entropy)与系统的能量分布有关,描述的是系统中不同的能量分布状态的可能性。
- 配置熵 与系统中微观结构的排列方式相关,描述的是组成部分如何在空间中排列的可能性。
例如,在分子动力学中,配置熵会与粒子在空间中的分布方式有关,而热熵则更多涉及能量的分布状态。这两种熵都可以一起影响系统的总熵。
5. 配置熵的重要性
-
化学反应与相变:在化学反应和相变过程中,配置熵通常起到重要作用。例如,在固态到液态的相变过程中,配置熵的变化可能驱动这种转变,因为液态通常有更多的原子或分子的排列方式,意味着更高的配置熵。
-
纳米材料与超分子系统:在复杂纳米材料或超分子体系中,配置熵可以显著影响其结构的稳定性和功能。例如,某些分子自组装成有序结构时,配置熵的作用至关重要。
-
生物系统:在生物大分子(如蛋白质或DNA)中,配置熵与其折叠和功能密切相关。蛋白质折叠的过程中,不同的构象对应不同的配置熵,而最终的折叠状态往往是熵和能量的平衡。
6. 配置熵与吉布斯自由能
配置熵直接影响系统的自由能。根据吉布斯自由能公式:
G=H−TS
其中 H 是焓,T 是温度,S 是熵。在许多过程中,系统会趋向于最小化吉布斯自由能。因此,系统可能通过增加配置熵来降低吉布斯自由能。例如,混合物的熵增大可以降低吉布斯自由能,从而使得混合物更加稳定。
总结:配置熵描述的是系统中组成部分如何排列的多样性与可能性。它与系统的微观排列有关,影响了材料的相变、反应动力学和热力学稳定性。在化学、物理和材料科学中,理解配置熵对于预测系统行为和稳定性至关重要。
相关文章:
如何理解Configurational entropy
Configurational entropy 是热力学和统计力学中的一个重要概念,它描述的是系统中由于其微观状态排列(即配置)导致的不确定性或混乱程度。不同于热力学中的热熵(thermal entropy),它特指那些与系统中的粒子、…...

H5端接入萤石监控
官方文档 EZOPEN协议 下滑至-平台架构 web/h5端使用文档 <template><div :id"video-container${index}${index2}" class"w-full bg-black"></div> </template><script>export default {data() {return {EZVIZAToken:…...

SSD1306 OLED显示屏驱动方案简介
SSD1306是一种常见的单色OLED(有机发光二极管)显示屏驱动芯片。以下从它的基本特点、工作原理和应用领域进行详细介绍: 一、基本特点 1. 尺寸与分辨率: SSD1306芯片支持多种尺寸的OLED显示屏,常见的有0.96寸、1.3寸等。不同尺寸的屏幕具有不…...

React18快速入门
需要先安装并配置React相关的工具和插件 下载安装Node.js,这里以MacOS Node.js v22.6.0为例 终端命令行检查是否安装成功 node -v npm -vNode.js快速入门 npm设置镜像源 #设置为阿里镜像源 npm config set registry https://registry.npmmirror.com #查看是否生…...

Day11笔记-字典基本使用系统功能字典推导式
二、字典【重点掌握】 1.概念 列表和元组的使用缺点:当存储的数据要动态添加、删除的时候,我们一般使用列表,但是列表有时会遇到一些麻烦,定位元素比较麻烦 # 一个列表/元组保存5个学生的成绩, score_list [66,100,70,78,99] sc…...

Ribbon (WPF)
Ribbon (WPF) 在本文中主要包含以下内容: Ribbon组件和功能应用程序菜单快速访问工具栏增强的工具提示 Ribbon是一个命令栏,它将应用程序的功能组织到应用程序窗口顶部的一系列选项卡中。Ribbon用户界面(UI)增加了特性和功能的可发现性,使用…...

解锁编程潜力,从掌握GitHub开始
目录: 一、搜索开源项目 1、什么是Git 2、Github常用词含义 3、一个完整的项目界面 4、使用Github搜索项目 1)in关键词 2)star或fork数量去查找 3)awesome加强搜索 二、访问速度慢的解决 1、使用网易UU加速器 2、使用…...

HTML转义字符对照表
HTML特殊字符转义对照表一 字符十进制转义字符字符十进制转义字符""&&<<<à>>>不断开空格 ?¡¡Ááâ⢢¢ˆ£££&…...
】)
【zabbix监控软件(配置及常用键值)】
监控软件–zabbix 同类产品:nagios、cacti 简介:能够部署企业级监控平台。 监控范围 1)zabbix SNMP 监控网络设备 防火墙、交换机 2)zabbix agent 监控 服务器:raid插槽 CPU 内存插槽 温度 风扇 操作系统࿱…...

98、RS485全自动收发电路入坑笔记
因为RS485采用叉分信号,只支持半双工。正常的RS485芯片驱动电路是需要GPIO来切换发送和接收模式。如下图所示,一般的RS485电平转换芯片都有RE/DE脚,用来切换收发模式。 例如这篇推荐:芯片RS485自动收发电路常见问题与应对策略 但…...
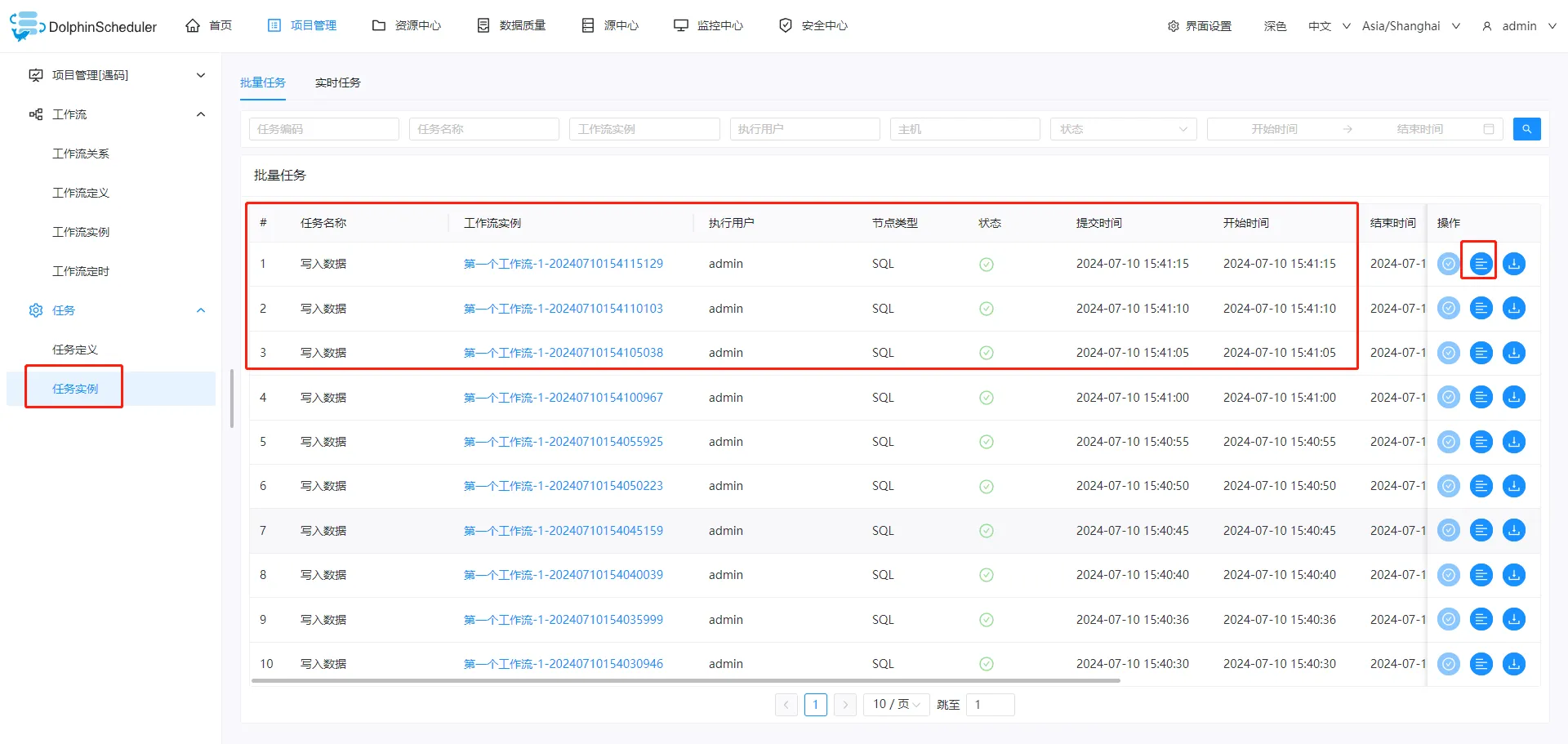
单机快速部署开源、免费的分布式任务调度系统——Apache DolphinScheduler
本文主要为大家介绍Apache DolphinScheduler的单机部署方式,方便大家快速体验。 环境准备 需要Java环境,这是一个老生常谈的问题,关于Java环境的安装与配置期望大家都可以熟练掌握。 验证java环境 java -version 下载安装包并解压 使用wg…...

【运维监控】Prometheus+grafana监控zookeeper运行情况
运维监控系列文章入口:【运维监控】系列文章汇总索引 文章目录 一、prometheus二、grafana三、prometheus集成grafana监控zookeeper1、修改zookeeper配置2、修改prometheus配置3、导入grafana模板4、验证 本示例通过zookeeper自带的监控信息暴露出来,然后…...

【C++二分查找】2560. 打家劫舍 IV
本文涉及的基础知识点 C二分查找 LeetCode2560. 打家劫舍 IV 沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。 由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。 小偷的 窃取能力 定义为他在…...

位段、枚举、联合
位段 在一个结构体中以位(最小单位)为单位来指定其成员所占的内存长度。位段成员名后面有一个冒号,冒号后有一个数字(这个数字是小于等于这个成员所占的位)。 typedef struct S {char a : 2;//8char b : 8;//8char c …...

golang学习笔记15——golang依赖管理方法
推荐学习文档 golang应用级os框架,欢迎star基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总golang学习笔记01——基本数据类型golang学习笔记02——gin框架及基本原理golang学习笔记03——gin框架的核心数据结构golang学…...

Linux 挂载磁盘与开机自动挂载操作指南
Linux 挂载磁盘与开机自动挂载操作指南 文章目录 Linux 挂载磁盘与开机自动挂载操作指南一 挂载磁盘1 查看硬盘信息2 新增数据盘执行分区3 新建分区4 创建一个主分区5 分区编号6 初始磁柱编号7 截止磁柱编号8 查看新建分区信息9 分区结果写入10 新分区同步操作系统11 设置新分区…...
『功能项目』单例模式框架【37】
我们打开上一篇36C#拓展 - 优化冗余脚本的项目, 本章要做的事情是编写单例模式基类,让继承其基类的子类在运行时只存在一个,共有两个单例基类框架,分别是不继承MonoBehaviour的单例和继承MonoBehaviour的单例框架 首先编写不继承…...

【计算机网络 - 基础问题】每日 3 题(三)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏&…...

SpringCloud Nacos
**************************** 准备工作 首先准备号nacos的镜像 根据镜像创建nacos容器 nacos:container_name: nacosimage: nacos/nacos-server:v2.1.0-slimports: #需要监听三个端口- "8848:8848"- "9848:9848"- "9849:9849"privileged: tr…...

机器学习算法详细解读和python实现
文章目录 一、机器学习概述1.1 机器学习的定义与分类机器学习的分类 1.2 机器学习的基本流程1.3 Python在机器学习中的应用Python的优势Python在机器学习中的应用场景 2.1 线性回归的基本概念线性回归的数学表达线性回归的目标 2.2 最小二乘法技术最小二乘法的数学推导最小二乘…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
