数学建模笔记—— 多目标规划
数学建模笔记—— 多目标规划
- 多目标规划
- 1. 模型原理
- 1.1 多目标规划的一般形式
- 1.2 多目标规划的解
- 1.3 多目标规划的求解
- 2. 典型例题
- 3. matlab代码实现
多目标规划
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。通常记为 MOP(multi-objective programming)。
多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。多目标最优化思想,最早是在1896年由法国经济学家V.帕雷托提出来的。他从政治经济学的角度考虑把本质上是不可比较的许多目标化成单个目标的最优化问题,从而涉及了多目标规划问题和多目标的概念。
1. 模型原理
1.1 多目标规划的一般形式
多目标规划是多目标决策的重要内容之一,在进行多目标决策时,当希望每个目标都尽可能的大(或尽可能够小)时,就形成了一个多目标规划问题,其一般形式为:
min f ( x ) = [ f 1 ( x ) , f 2 ( x ) , ⋯ , f m ( x ) ] T , s . t . { g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , p , h j ( x ) = 0 , j = 1 , 2 , ⋯ , q , \begin{array}{rl}\min&\mathrm{f(x)=[f_1(x),~f_2(x),\cdots,f_m(x)]^T,}\\\mathrm{s.t.}&\begin{cases}\mathrm{g_i(x)\leq0,}&\mathrm{i=1,2,\cdots,p,}\\\mathrm{h_j(x)=0,}&\mathrm{j=1,2,\cdots,q,}\end{cases}\end{array} mins.t.f(x)=[f1(x), f2(x),⋯,fm(x)]T,{gi(x)≤0,hj(x)=0,i=1,2,⋯,p,j=1,2,⋯,q,
- 其中 x x x为决策向量, f 1 ( x ) , f 2 ( x ) , ⋯ , f m ( x ) f_1(x),f_2(x),\cdots,f_m(x) f1(x),f2(x),⋯,fm(x)为目标函数s. t . t. t.式为约束条件
- 记 Ω = { x ∣ g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , p ; h j ( x ) = 0 , j = 1 , 2 , ⋯ , q } \begin{aligned}&\text{记}\Omega=\{x|g_{i}(x)\leq0, i=1,2,\cdots,p; h_{j}(x)=0, j=1,2,\cdots,q\}\end{aligned} 记Ω={x∣gi(x)≤0,i=1,2,⋯,p;hj(x)=0,j=1,2,⋯,q}
- 称 Ω \Omega Ω为多目标规划的可行域(决策空间), f ( Ω ) = f(\Omega)= f(Ω)= { f ( x ) ∣ x ∈ Ω } \{f(x)|x\in\Omega\} {f(x)∣x∈Ω}为多目标规划问题的像集(目标空间),多目标规划问题以下简称问题(MP)。
1.2 多目标规划的解
-
最优解定义
设 x ˉ ∈ Ω \bar{x}\in\Omega xˉ∈Ω, 若对于任意 i = 1 , 2 , ⋅ ⋅ ⋅ , m i=1,2,\cdotp\cdotp\cdotp,m i=1,2,⋅⋅⋅,m及任意 x ∈ Ω x\in\Omega x∈Ω,均有
f i ( x ˉ ) ≤ f i ( x ) f_i(\bar{x})\leq f_i(x) fi(xˉ)≤fi(x)
则称 x ˉ \bar{x} xˉ为问题(MP)的绝对最优解,记问题(MP)的绝对最优解集为 Ω a b ∗ \Omega_\mathrm{ab}^* Ωab∗一般来说,多目标规划问题的绝对最优解是不常见的,当绝对最优解不存在时,需要引入新的“解”的概念。多目标规划中最常用的解为非劣解或有效解,也称为Pareto最优解。
-
有效解定义
考虑多目标规划问题(MP),设 x ˉ ∈ Ω ^ \bar{x}\in\widehat{\Omega} xˉ∈Ω ,若不存在 x ∈ Ω ^ x\in\widehat{\Omega} x∈Ω ,使得
f i ( x ) ≤ f i ( x ˉ ) , i = 1 , 2 , ⋯ , m , f_{i}(x)\leq f_{i}(\bar{x}),\quad i=1,2,\cdots,m, fi(x)≤fi(xˉ),i=1,2,⋯,m,
且至少有一个
f j ( x ) < f j ( x ˉ ) , f_j(x)<f_j(\bar{x}), fj(x)<fj(xˉ),
则称 x ˉ \bar{x} xˉ为问题(MP)的有效解(或Pareto有效解), f ( x ˉ ) f(\bar{x}) f(xˉ)为有效点。 -
满意解定义
主要是从决策过程角度,根据决策者的偏好与要求而提出的。设可行域为 Ω \Omega Ω,要求 m m m个目标函数 f i ( i = 1 , 2 , ⋯ , m ) f_i(i=1,2,\cdots,m) fi(i=1,2,⋯,m)越小越好。有时决策者的期望较低,给出了 m m m个阈值 α i \alpha_i αi, 当 x ˉ ∈ Ω \bar{x}\in\Omega xˉ∈Ω满足 f i ( x ˉ ) ≤ α i ( i = 1 , 2 , ⋯ , m ) f_i(\bar{x})\leq\alpha_i(i=1,2,\cdots,m) fi(xˉ)≤αi(i=1,2,⋯,m)时,就认为 x ˉ \bar{x} xˉ是可以接受的、是满意的。这样的 x ˉ \bar{x} xˉ就称为一个满意解。
1.3 多目标规划的求解
由于对绝大多数多目标决策实际问题,决策者最偏好的方案都是有效解,下面介绍几种常用的求解问题(MP)的有效解的常用方法
值得注意的是,在多目标规划中,除去目标函数一般是彼此冲突外,还有另一个特点:目标函数的不可公度性。所以通常在求解前,先对目标函数进行预处理。预处理的内容包括:无量纲化处理,归一化处理等
MP问题求解有效解的常用方法
-
线性加权法
该方法的基本思想是根据目标的重要性确定一个权重,以目标函数的加权平均值为评价函数,使其达到最优。权重的确定一般由决策者给出,因而具有较大的主观性,不同的决策者给的权重可能不同,从而会使计算的结果不同。
-
ε \varepsilon ε约束法
根据决策者的偏好,选择一个主要关注的参考目标,而将其他目标函数放到约束条件中。约束法也称主要目标法或参考目标法,参数E是决策者对变为约束条件的目标函数的容许接受阈值。
-
理想点法
该方法的基本思想是:以每个单目标最优值为该目标的理想值,使每个目标函数值与理想值的差的加权平方和最小。
-
优先级法
该方法的基本思想是根据目标重要性分成不同优先级,先求优先级高的目标函数的最优值,在确保优先级高的目标获得不低于最优值的条件下,再求优先级低的目标函数
线性加权法详解:
若一个规划问题中有多个目标,我们可以对多目标函数进行加权组合使问题变为单目标规划,然后再利用之前学习的解法进行求解
线性加权法具体步骤如下:
- 确定每个目标的权系数。
0 ≤ w j ≤ 1 , j = 1 , 2 , ⋯ , m ; ∑ j = 1 m w j = 1 0\leq w_j\leq 1, j= 1, 2, \cdots , m;\quad\sum _{j= 1}^mw_j= 1 0≤wj≤1,j=1,2,⋯,m;j=1∑mwj=1
-
写出评价函数
∑ j = 1 m w j f j \sum_{j=1}^{m}w_{j}f_{j} j=1∑mwjfj -
求评价函数最优值
m i n ∑ i = 1 m w i f i ( x ) , s . t . x ∈ Ω . \begin{array}{ll}min&\sum_{i=1}^{m}w_{i}f_{i}(x),\\\mathrm{s.t.}&\mathbf{x}\in\mathbf{\Omega}.\end{array} mins.t.∑i=1mwifi(x),x∈Ω.
注意:
- 要将多个目标函数统一为最大化和最小化问题(不同的加“-” 号)才可以进行加权组合
- 如果目标函数量纲不同,则需要对其进行标准化再进行加权,标准化的方法一般是目标函数除以某一个常量,该常量是这个目标函数的某个取值,具体取何值可根据经验确定
- 对多目标函数进行加权求和是,权重一般由该领域专家给定,实际比赛中,若无特殊说明,我们可令权重相同
2. 典型例题
某化工厂今年拟生产两种新产品A和B,其生产费用分别为2万元/吨和5万元/吨。这两种产品均将造成环境污染,每生产一吨A产品会产生0.4吨的污染,每生产一吨B产品会产生0.3吨的污染。由于条件限制,工厂生产产品A和B的最大生产能力各为每月5吨和6吨,而市场需要这两种产品的总量每月不少于7吨。该工厂决策认为,这两个目标中环境污染应该优先考虑,且根据经验生产费用的参考值为30万元,污染量参考值为2吨。试问工厂如何安排生产计划,在满足市场需要的前提下,使设备的花费和产生的污染均达到最小。
设工厂每月产品A生产 x 1 x_1 x1吨,B生产 x 2 x_2 x2吨,那么产生的污染分别为0.4 x 1 x_1 x1吨和0.3 x 2 x_2 x2吨
建立多目标规划模型:
{ min f 1 = 2 x 1 + 5 x 2 min f 2 = 0.4 x 1 + 0.3 x 2 s t . { x 1 + x 2 ≥ 7 0 ≤ x 1 ≤ 5 0 ≤ x 2 ≤ 6 \begin{cases}\min\:f_1=2x_1+5x_2\\\min\:f_2=0.4x_1+0.3x_2\\st.\begin{cases}x_1+x_2\geq7\\0\leq x_1\leq5\\0\leq x_2\leq6\end{cases}\end{cases} ⎩ ⎨ ⎧minf1=2x1+5x2minf2=0.4x1+0.3x2st.⎩ ⎨ ⎧x1+x2≥70≤x1≤50≤x2≤6
下面我们将其转换为一个单目标规划问题,即对上面的两个目标函数进行加权,由于该工厂决策认为环境污染应优先考虑,因此我们可以选取 f 1 f_1 f1和 f 2 f_2 f2的权重分别为0.4和0.6。注意到两个目标函数的单位不同,一个为“万元”,一个为“吨”,因此我们需要首先对目标函数进行标准化来消除量纲的影响,然后再进行加权,由于题目中已经给了产品费用和污染量的参考值,因此我们将这两个目标函数分别除以其参考值来消除量纲。
加权后的目标函数:
f = 0.4 × f 1 30 + 0.6 × f 2 2 = 0.4 30 × ( 2 x 1 + 5 x 2 ) + 0.6 2 × ( 0.4 x 1 + 0.3 x 2 ) f=0.4\times\frac{f_{1}}{30}+0.6\times\frac{f_{2}}{2}=\frac{0.4}{30}\times(2x_{1}+5x_{2})+\frac{0.6}{2}\times(0.4x_{1}+0.3x_{2}) f=0.4×30f1+0.6×2f2=300.4×(2x1+5x2)+20.6×(0.4x1+0.3x2)
敏感性分析:
下面我们对结果进行敏感性分析,敏感性分析是指从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。其实质是通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小的规律。
我们改变 f 1 f_1 f1和 f 2 f_2 f2的权重,来观察对结果的影响。(由于两个权重和为1,因此我们只需要改变 f 1 f_1 f1的权重即可),下面是图形:


可以看出, f 1 f_1 f1的权重的转折点在0.333-0.334之间,当 f 1 f_1 f1的权重小于这个转折点时, x 1 = 1 , x 2 = x_1=1,x_2= x1=1,x2= 6,大于转折点时, x 1 = 5 , x 2 = 2 x_1=5,x_2=2 x1=5,x2=2。其主要原因是:当 f 1 f_1 f1的权重越小时,厂家对环境污染的权重就越大,那么厂家就更加倾向于生产污染较少的产品B,尽管B的生产费用要远高于产品A。
3. matlab代码实现
多目标规划模型的求解
%% 多目标规划问题
clc
clear
% 两个目标权重
w1=0.4;
w2=0.6;
c=[w1/30*2+w2/2*0.4;w1/30*5+w2/2*0.3];
% 不等式约束
A=[-1,-1];
b=-7;
% 上下界
lb=[0 0]';
ub=[5 6]';
% 求解
[x,fval]=linprog(c,A,b,[],[],lb,ub)
f1=2*x(1)+5*x(2)
f2=0.4*x(1)+0.3*x(2)
输出:
找到最优解。x =52fval =1.0467f1 =20f2 =2.6000
敏感性分析:
%% 敏感性分析
clear
clc
W1=0.1:0.001:0.5;
W2=1-W1;
n=length(W1);
F1=zeros(n,1);
F2=zeros(n,1);
X1=zeros(n,1);
X2=zeros(n,1);
FVAL=zeros(n,1);
A=[-1,-1];
b=-7;
lb=[0 0];
ub=[5 6];
for i=1:nw1=W1(i);w2=W2(i);c=[w1/30*2+w2/2*0.4;w1/30*5+w2/2*0.3];[x,fval]=linprog(c,A,b,[],[],lb,ub);F1(i)=2*x(1)+5*x(2);F2(i)=0.4*x(1)+0.3*x(2);X1(i)=x(1);X2(i)=x(2);FVAL(i)=fval;
end
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')figure(3)
plot(W1,FVAL)% 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
输出:
figure1:

figure2:

figure3:
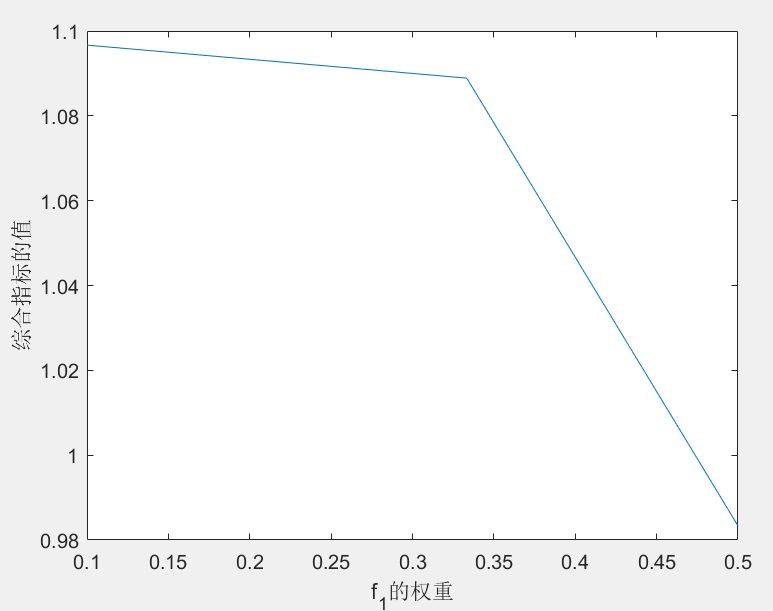
相关文章:

数学建模笔记—— 多目标规划
数学建模笔记—— 多目标规划 多目标规划1. 模型原理1.1 多目标规划的一般形式1.2 多目标规划的解1.3 多目标规划的求解 2. 典型例题3. matlab代码实现 多目标规划 多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。通常记为 …...

【鸿蒙HarmonyOS NEXT】页面之间相互传递参数
【鸿蒙HarmonyOS NEXT】页面之间相互传递参数 一、环境说明二、页面之间相互传参 一、环境说明 DevEco Studio 版本: API版本:以12为主 二、页面之间相互传参 说明: 页面间的导航可以通过页面路由router模块来实现。页面路由模块根据页…...

SonicWall SSL VPN曝出高危漏洞,可能导致防火墙崩溃
近日,有黑客利用 SonicWall SonicOS 防火墙设备中的一个关键安全漏洞入侵受害者的网络。 这个不当访问控制漏洞被追踪为 CVE-2024-40766,影响到第 5 代、第 6 代和第 7 代防火墙。SonicWall于8月22日对其进行了修补,并警告称其只影响防火墙的…...
采购订单信息)
关于SAP标准委外(带料外协)采购订单信息
业务背景: 业务部门提出需要将售料外协方式变更为带料外协,带料外协实际业务存在一个委外订单存在多次发料,且每次发票需要进行齐套发料,不同批次的发料涉及物料替代。在半成品收货时需要进行对发料的组件进行扣料。 需求分析&a…...

SpringBoot整合WebSocket实现消息推送或聊天功能示例
最近在做一个功能,就是需要实时给用户推送消息,所以就需要用到 websocket springboot 接入 websocket 非常简单,只需要下面几个配置即可 pom 文件 <!-- spring-boot-web启动器 --><dependency><groupId>org.springframewo…...

使用 QEMU 模拟器运行 FreeRTOS 实时操作系统
文章目录 QEMU 官网QEMU 文档QEMU 简介QEMU 安装QEMU 命令启动虚拟机串口控制台监控命令行 FreeRTOS安装编译工具FreeRTOS 源码RISC-V-Qemu-virt_GCC 示例编译 RISC-V-Qemu-virt_GCC启动虚拟机运行 FreeRTOS QEMU 官网 https://www.qemu.org/ QEMU 文档 https://www.qemu.or…...

Oracle EBS中AR模块的财务流程概览
应收账款 (AR) 模块是Oracle E-Business Suite (EBS) 中另一个重要的财务管理模块,主要用于管理企业销售过程中的账款回收。下面是AR模块中的一些关键财务流程及其详细说明: 1. 销售订单管理 创建销售订单:当客户下单时,销售人员…...

Minitab 的直方图结果分析解释
Minitab 的直方图结果分析解释 步骤 1:评估关键特征 检查分布的尖峰和散布。评估样本数量对直方图外观的影响。 标识尖峰(即,条的最高聚类): 尖峰表示样本中最常见的值。评估样本的散布以了解数据的变异程度。例如…...

AgentRE:用智能体框架提升知识图谱构建效果,重点是开源!
发布时间:2024 年 09 月 13 日 Agent应用 AgentRE: An Agent-Based Framework for Navigating Complex Information Landscapes in Relation Extraction 在复杂场景中,关系抽取 (RE) 因关系类型多样和实体间关系模糊而挑战重重,影响了传统 “…...

力扣题解2390
大家好,欢迎来到无限大的频道。 今日继续给大家带来力扣题解。 题目描述(中等): 从字符串中移除星号 给你一个包含若干星号 * 的字符串 s 。 在一步操作中,你可以: 选中 s 中的一个星号。 移除星号…...

用Python获取PDF页面的大小、方向和旋转角度
在文档管理和自动化领域,了解PDF文档的内在属性(如页面大小、方向和旋转角度)对于确保一致的文档处理和布局保真度至关重要。这些属性在内容重用、归档以及PDF无缝集成到网络环境或其他数字工作流程中起着关键作用,因为它们直接影…...

【即时通讯】轮询方式实现
技术栈 LayUI、jQuery实现前端效果。django4.2、django-ninja实现后端接口。 代码仓 - 后端 代码仓 - 前端 实现功能 首次访问页面并发送消息时需要设置昵称发送内容为空时要提示用户不能发送空消息前端定时获取消息,然后展示在页面上。 效果展示 首次发送需要…...

Flock 明牌空投教程
FLock 旨在为人工智能构建一个去中心化的隐私保护解决方案。FLock提出了一项名为联合学习区块(简称 FLocks)的研究计划,该计划使用区块链作为数据持有者之间的协调平台来进行机器学习,同时数据保持本地和隐私。通过用区块链取代收…...

项目内部调用的远程接口开发
编写一个项目内部调用的远程接口通常是为了在分布式系统或者微服务架构中,实现各个服务之间的通信和数据交换。这样的远程接口专门用于服务之间的调用,而不是直接暴露给外部用户或前端。 项目内部的远程接口统一放在api工程 首先进入api编写接口&#x…...

影响IP代理池稳定性的因素有哪些?
IP代理池在提供网络服务时,稳定性是一项决定性指标。多个外部和内部因素可能会影响这个稳定性,因此深入理解这些影响因素,可以帮助优化IP代理池的性能与服务质量。 1. IP来源质量 纯净度与使用频次:优质的IP来源常常被描述为纯净…...

基于Prometheus和Grafana的现代服务器监控体系构建
构建一个基于 Prometheus 和 Grafana 的现代服务器监控体系涉及多个步骤。以下是大体的流程和步骤说明: 1. Prometheus 监控系统 Prometheus 是一个开源的系统监控和报警工具,专门设计用于抓取时间序列数据。 1.1 Prometheus 的安装 Docker 安装 Prom…...

原生 input 中的 “type=file“ 上传文件
目标:实现文件上传功能 原型图: HTML部分: <div class"invoice-item"><div class"invoice-title">增值税专用发票</div><div class"invoice-box"><el-form-item label"标准…...

【Unity新闻】Unity的产品命名变化
快速回顾一下Unity产品命名的调整。 在2023年 Unity就宣布版本命名的变化,将使用Unity 6作为最新版本的命名。 具体的规则,在论坛里进行了说明。 以后正式的LTS版本就是Unity 6,将在2024年末发布。 而不管是之前的Runtime费还是今天的费用…...

《PostMan(一):配置全局令牌》
文章目录 一、配置全局token1、设置2、添加全局3、添加全局变量名称4、选中全局,并查看5、添加赋值脚本6、配置令牌取值7、即可成功获取用户信息 一、配置全局token 1、设置 2、添加全局 3、添加全局变量名称 4、选中全局,并查看 5、添加赋值脚本 // 把…...
如何理解Configurational entropy
Configurational entropy 是热力学和统计力学中的一个重要概念,它描述的是系统中由于其微观状态排列(即配置)导致的不确定性或混乱程度。不同于热力学中的热熵(thermal entropy),它特指那些与系统中的粒子、…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
