牛客练习赛128:Cidoai的平均数对(背包dp)
题目描述
给定 nnn 对数 (ai,bi)(a_i,b_i)(ai,bi) 和参数 kkk,你需要选出一些对使得在满足 bib_ibi 的平均值不超过 kkk 的同时,aia_iai 的和最大,求出这个最大值。
输入描述:
第一行两个整数分别表示 n,kn,kn,k。 接下来 nnn 行,每行两个数分别表示 ai,bia_i,b_iai,bi
输出描述:
一行一个整数表示答案。
示例1
输入
复制5 6 4 10 3 4 6 7 7 7 10 8
5 6 4 10 3 4 6 7 7 7 10 8
输出
复制16
16
备注:
0≤ai,bi,k≤500,1≤n≤5000 \le a_i,b_i,k \le 500,1 \le n \le 5000≤ai,bi,k≤500,1≤n≤500
做法
本题重点在这个平均数的处理。b1+b2+b3+……+bn<=n*k,也就是(b1-k)+(b2-k)+(b3-k)+……+(bn-k)<=0。那我们就先把bi全都减去k。那bi为负数的就可以全部拿下。这样一来,我们背包的容量就是bi为负数的总和的绝对值了。
#include<bits/stdc++.h>
using namespace std;
const int N=510,M=250010;
int n,k;
int a[N],b[N];
int dp[M];
int res,ans,sum,ans2;
struct ty{int a,b;
};
vector<ty> v;
int main(){scanf("%d%d",&n,&k);v.push_back({-1,-1});for(int i=1;i<=n;i++) {cin>>a[i]>>b[i];b[i]-=k;if(b[i]<=0) {ans+=a[i];sum+=-b[i];}else{v.push_back({a[i],b[i]});}}memset(dp,-0x3f,sizeof(dp));dp[0]=0;for(int i=1;i<v.size();i++){for(int j=sum;j>=0;j--){ if(j-v[i].b>=0)dp[j]=max(dp[j],dp[j-v[i].b]+v[i].a);}}for(int i=0;i<=sum;i++) ans2=max(dp[i],ans2);cout<<ans+ans2;
}
相关文章:
)
牛客练习赛128:Cidoai的平均数对(背包dp)
题目描述 给定 nnn 对数 (ai,bi)(a_i,b_i)(ai,bi) 和参数 kkk,你需要选出一些对使得在满足 bib_ibi 的平均值不超过 kkk 的同时,aia_iai 的和最大,求出这个最大值。 输入描述: 第一行两个整数分别表示 n,kn,kn,k。 接下来 nnn 行&…...

Python世界:简易地址簿增删查改算法实践
Python世界:简易地址簿增删查改算法实践 任务背景编码思路代码实现本文小结 任务背景 该任务来自简明Python教程中迈出下一步一章的问题: 编写一款你自己的命令行地址簿程序, 你可以用它浏览、 添加、 编辑、 删除或搜索你的联系人ÿ…...
网络安全-intigriti-0422-XSS-Challenge Write-up
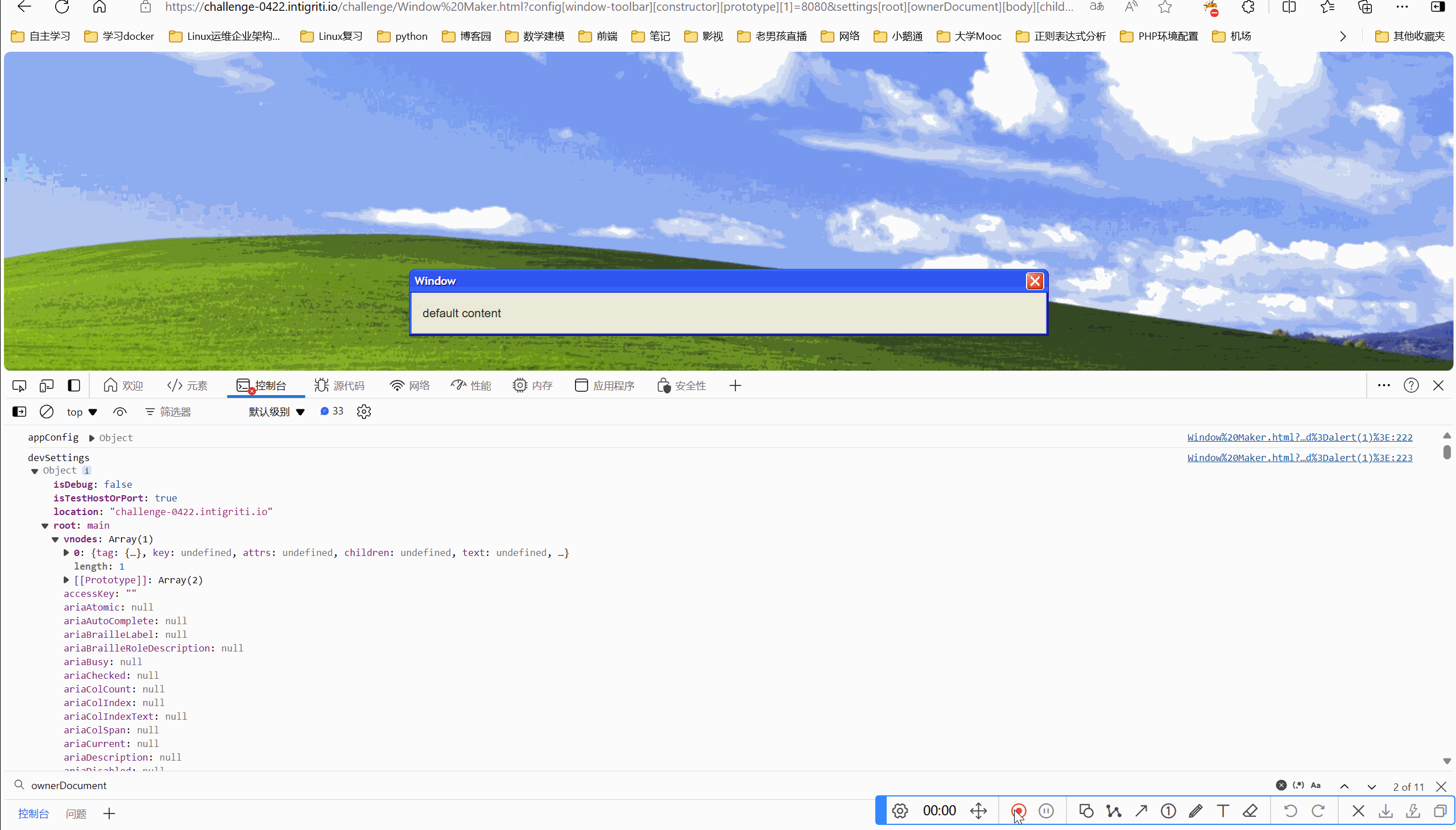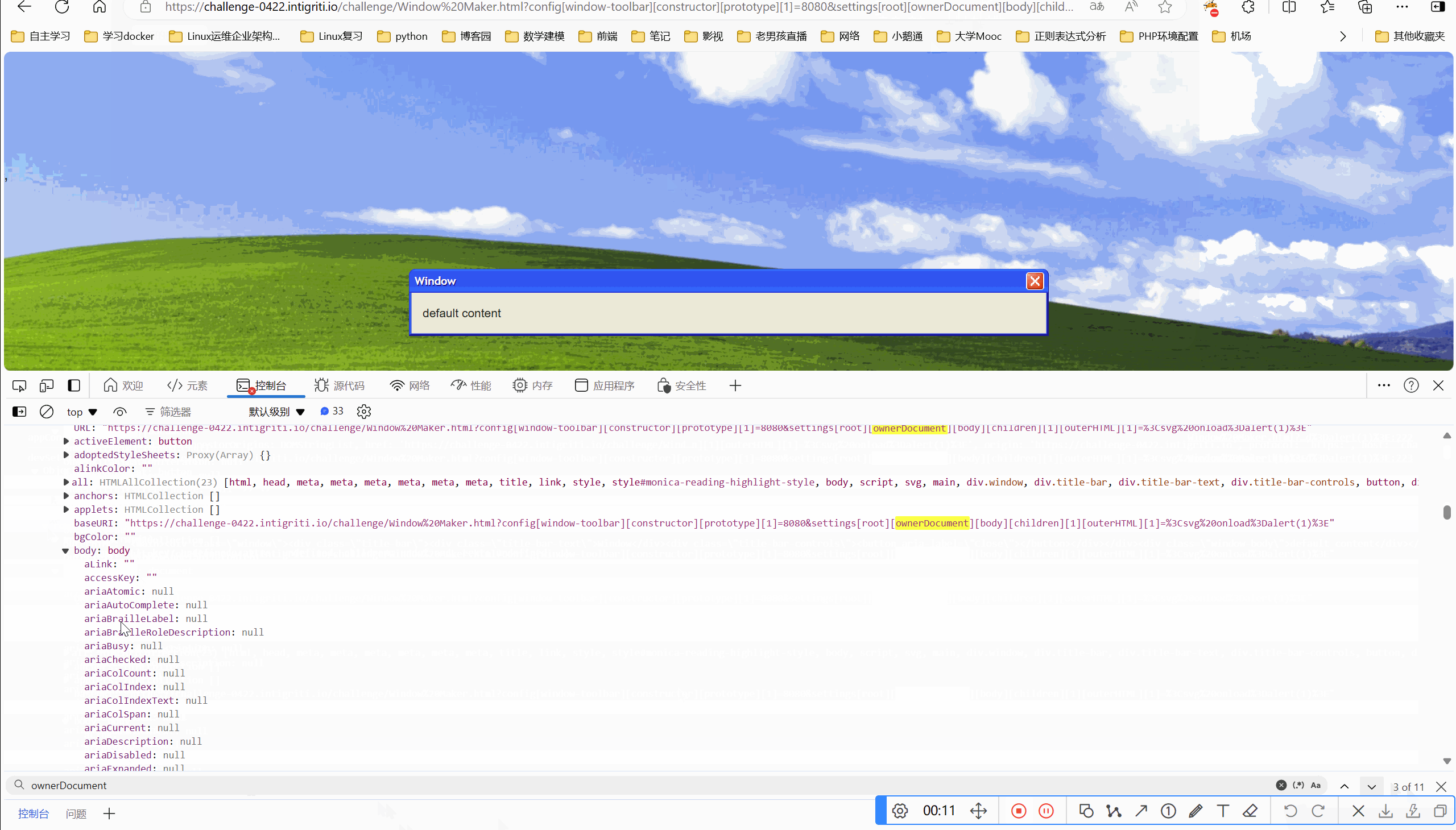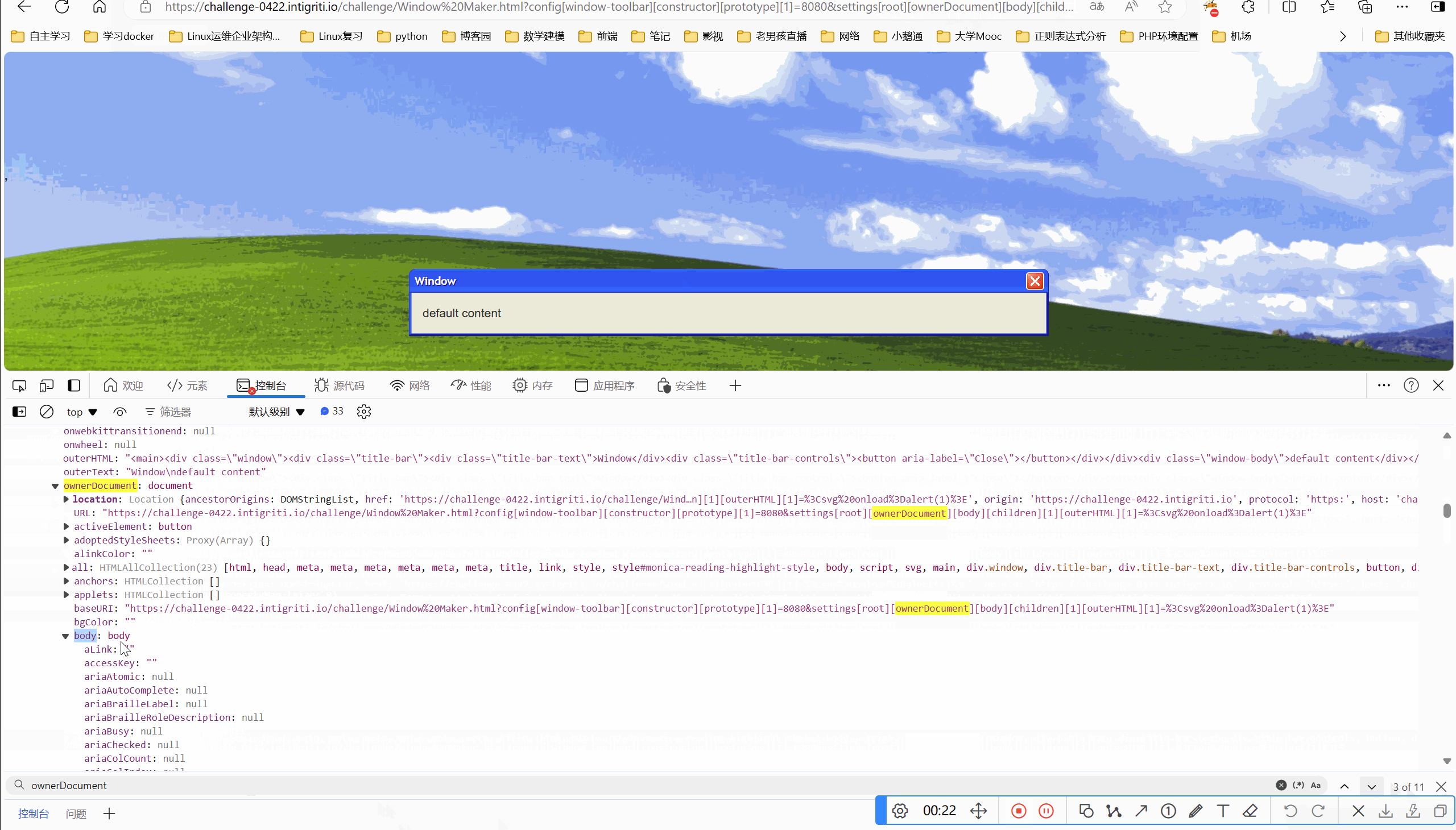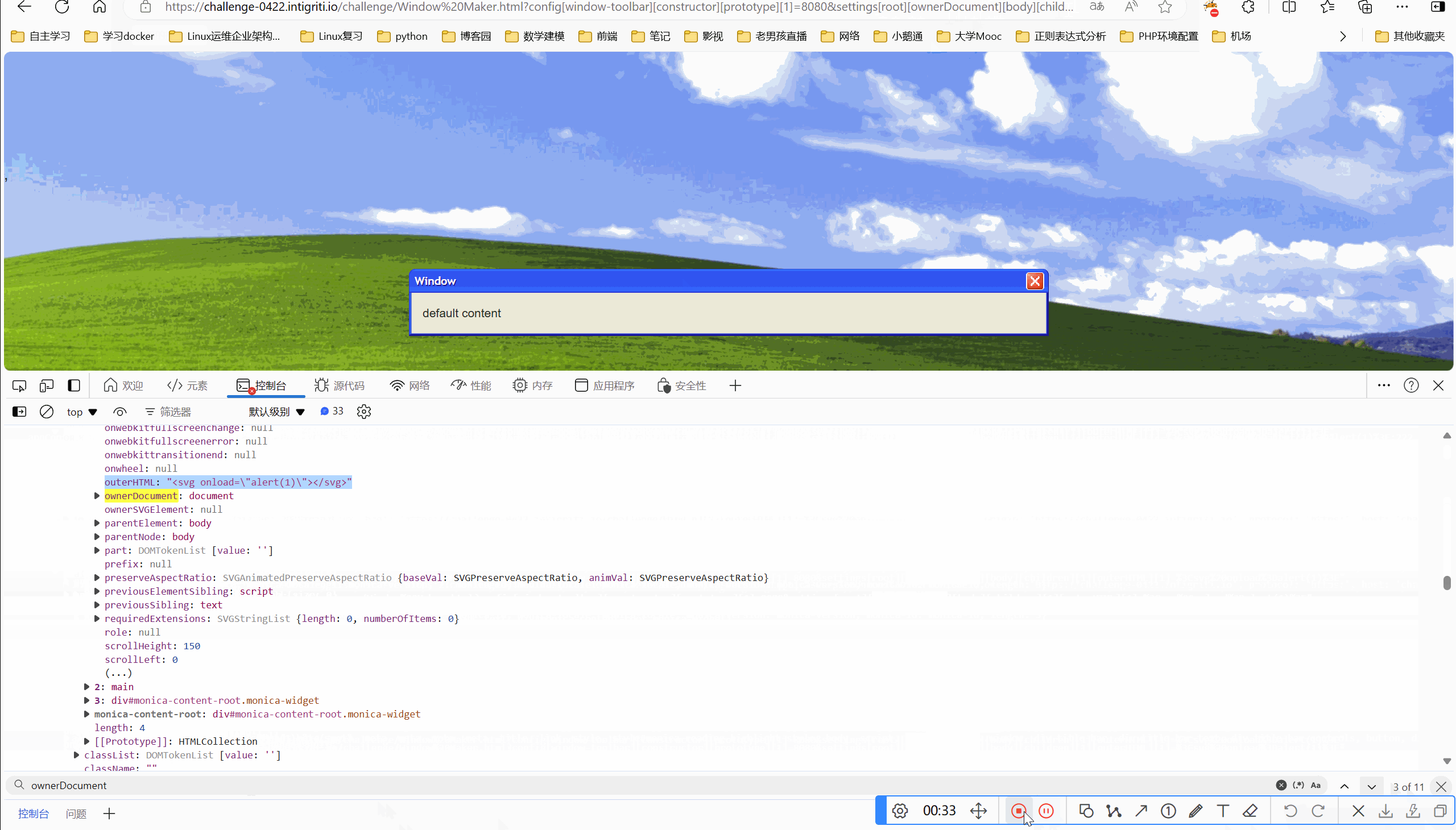
目录 一、环境 二、解题 2.1看源码 一、环境 Intigriti April Challenge 二、解题 要求:弹出域名就算成功 2.1看源码 我们看到marge方法,肯定是原型链污染题目 接的是传参,我们可控的点在于qs.config和qs.settings,这两个可…...

Debian Linux 11 使用crash
文章目录 前言一、环境安装1.1 安装debug package1.2 安装crash 二、使用crash 前言 # cat /etc/os-release PRETTY_NAME"Debian GNU/Linux 11 (bullseye)" NAME"Debian GNU/Linux" VERSION_ID"11" VERSION"11 (bullseye)" VERSION_C…...

python列表 — 按顺序找出b表中比a表多出的元素
目录 一、功能描述 二、适用场景 三、代码实现 一、功能描述 有a、b两个列表,a列表有3个元素;b列表有7个元素。b列表多出的一个元素可能在随机的位置,在不影响其他元素的情况下,找到b列表多出的那四个元素,并按照在…...

如何使用Python创建目录或文件路径列表
在 Python 中,创建目录或生成文件路径列表通常涉及使用 os、os.path 或 pathlib 模块。下面是一些常见的任务和方法,用于在 Python 中创建目录或获取文件路径列表。 问题背景 在初始阶段的 Python 学习过程中,可能遇到这样的问题:…...

领夹麦克风哪个品牌好,哪种领夹麦性价比高,无线麦克风推荐
在音频录制需求日益多样化的今天,无线领夹麦克风作为提升音质的关键设备,其重要性不言而喻。市场上鱼龙混杂,假冒伪劣、以次充好的现象屡见不鲜。这些产品往往以低价吸引消费者,却在音质、稳定性、耐用性等方面大打折扣࿰…...
)
苍穹外卖学习笔记(五)
文章目录 二.新增菜品1.图片上传2.具体新增菜品 二.新增菜品 1.图片上传 这里采用了阿里云oss对象存储服务 application.yml alioss:endpoint: ${sky.alioss.endpoint}access-key-id: ${sky.alioss.access-key-id}access-key-secret: ${sky.alioss.access-key-secret}bucket…...

什么是卷积层、池化层、BN层,有什么作用?
什么是卷积层、池化层、BN层,有什么作用? 卷积层池化层BN层 卷积层 定义: 卷积层是CNN中的核心组件,它通过卷积运算对输入数据进行特征提取。卷积层由多个卷积单元组成,每个卷积单元的参数通过反向传播算法优化得到。…...

[学习笔记]《CSAPP》深入理解计算机系统 - Chapter 4 处理器体系结构Chapter 5 优化程序性能
总结一些第四章和第五章的一些关键信息 Chapter 4 处理器体系结构将处理组织成阶段 Chapter 5 优化程序性能 Chapter 4 处理器体系结构 在硬件中,寄存器直接将它的输入和输出线连接到电路的其他盆。 在机器级变成中,寄存器代表的是 CPU 中为数不多的可寻…...

案例分享|我是这样转型做数据产品经理的?
本文为才聚学员投稿的原创作品,现在才聚正面向专业项目管理者征集“项目管理实战案例”原创文章,被采纳即可获得丰厚稿酬,欢迎大家关注公众号踊跃投稿。 如您有意向投稿,可将稿件投递给我们。 故事介绍 三段故事,讲…...

ffmpeg面向对象-rtsp拉流相关对象
目录 1.AVFormatContext和FFFormatContext类。1.1 概述1.2 构造函数1.3 oopc的继承实现 2. AVInputFormat 类。2.1 多态的实现 3.所用设计模式3.1模板模式3.2 工厂模式? 3.3 rtsp拉流建链 4.this指针5.小结6.rtsp拉流流程 1.AVFormatContext和FFFormatContext类。 …...

feign client发送Post请求,发送对象参数,服务端接收不到正确参数报错排查
记一次feignclient发送请求服务端接收不到正确参数排查 服务端代码: Operation(summary "Create team")PostMapping("post")RequiresPermissions("team:add")public RestResponse addTeam(Valid Team team) {this.teamService.crea…...

Hadoop林子雨安装
文章目录 hadoop安装教程注意事项: hadoop安装教程 链接: 安装教程 注意事项: 可以先安装ububtu增强功能,完成共享粘贴板和共享文件夹 ubuntu增强功能 2.这里就可以使用共享文件夹 或者在虚拟机浏览器,用 微信文件传输助手 传文…...
Springboot项目总结
1.为了调用写在其他包里面的类的方法 但是不使用new来实现调用这个类里面的方法,这个时候我们就需要将这个类注入到ioc容器里面,通过ioc容器来实现自动生成一个对象。 对ioc容器的理解:自动将一个对象实现new. 考察了and 和 or组合使用&…...

目标检测从入门到精通——数据增强方法总结
以下是YOLO系列算法(从YOLOv1到YOLOv7)中使用的数据增强方法的总结,包括每种方法的数学原理、相关论文以及对应的YOLO版本。 YOLO系列数据增强方法总结 数据增强方法数学原理相关论文图像缩放将输入图像缩放到固定大小(如448x44…...

SQL server 的异常处理 一个SQL异常 如何不影响其他SQL执行
在 SQL Server 中,存储过程中的 SQL 语句是顺序执行的。如果其中任何一个 SQL 语句遇到了错误或异常,那么默认情况下,这个错误会导致整个事务(如果有的话)回滚,并且存储过程会立即停止执行,不会…...

STM32——看门狗通俗解析
笔者在学习看门狗的视频后,对看门狗仍然是一知半解,后面在实际应用中发现它是一个很好用的检测或者调试工具。所以总结一下笔者作为初学小白对看门狗的理解。 主函数初始化阶段、循环阶段和复位 众所周知,程序的运行一般是这样的࿱…...

点亮第一盏LED灯 5): stm32CubeMX生成Keil代码
嵌入式入门,继续点亮第一盏LED灯,前面文章已经配置了GPIO引脚和时钟,那么基本上stm32CubeMX的配置就完成了,还有一点就是可以对PC13这个引脚起个别名, 这里起的别名是 LED_PC13,还有注意地方就是GPIO mode…...

ollama语言大模型部署使用
ollama语言大模型部署使用 前言一、下载安装maxkb1、下载解压赋权2、安装 二、安装ollamadocker运行 三、无需获取api_keymaxkb安装ollama模型对,就是这,你选好基础模型后,只需要给他地址,添加完成后自行调用ollama安装你选择好的…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
