(算法基础)Floyd算法
适用情景
Floyd算法适用于多源汇最短路,也就是他问你比如说从3号点到6号点的最短路距离,比如说从7号点到20号点的最短路距离,而不是单源最短路(从1号点到n号点的最短路距离)。在这个算法当中允许负权边的存在。但在求最短路距离当中(包括其他算法也一样)是不能够出现负环的,因为这样最短路距离可能变到负无穷去了
时间复杂度
三重无脑循环,显然O(N^3)。
算法解释
首先,对于Floyd算法来说,对于图的存储必须要用邻接矩阵来存,不能用邻接表。然后对于邻接矩阵,一开始当然得初始化,这边必须得注意:由于是图,这个矩阵无论是行还是列,有效位都是从一开始。
int dist[N][N]; //N表示图中点的个数+1然后Floyd算法是允许这个图当中存在负权边,但是不能出现负环(因为在最短路问题当中的话,一旦出现负环,最短路可能变成负无穷)。然后需要对dist数组初始化,这边再提一句:我们现在已经是默认图当中没有负环,好那么现在如果说存在自环的话,肯定是正的,在最短路当中那就不予考虑,于是在初始化的过程当中,如果说i等于j,直接就是0,其他的话就初始化成正无穷,为什么要正无穷?想想就知道了,等会儿我肯定需要min操作嘛
for (int i=1;i<=n;i++)
{for (int j=1;j<=n;j++){if (i==j){dist[i][j]=0;}else{dist[i][j]=0x3f3f3f3f;}}
}然后当往这个邻接矩阵当中去输入一条一条图当中的边的时候,由于我们现在是最短路问题,因此我们只需要取小的就可以了,然后如果是自环的话,所以我们默认是没有负环的,因此取小后就是0
while(m--)
{scanf("%d %d %d",&a,&b,&c);dist[a][b]=MIN(dist[a][b],c);
}然后接下来就是执行Floyd算法,其实就是三重循环,外循环k从1到n,第二层循环i从1到n,第三层循环j从1到n。然后每一层循环的话就如下比较一下,至于原理的话,这个是与动态规划有关,像我现在的话也掌握不了,先把算法的步骤先记牢吧
for (int k=1;k<=n;k++)
{for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){dist[i][j]=MIN(dist[i][j],dist[i][k]+dist[k][j]);}}
}然后当这三重循环结束之后,原先dist数组是用来存边的,现在他已经像孙悟空变身一样,变成了从i到j的最短距离了。当然也有可能的情况就是从i到j的话是走不到的,这时候还谈个屁最短路啊,那如何去判断走不到的这种情况呢?由于是允许存在负权边的情况,因此当在更新的时候有可能会把这个无穷大的值稍微更新了小了一些,因此不能直接dist[ i ][ j ] 等于 0x3f3f3f3f
while(k--)
{scanf("%d %d",&a,&b);if(dist[a][b]>0x3f3f3f3f/2){printf("impossible\n");}else{printf("%d\n",dist[a][b]);}
}例题
来源:AcWing
854. Floyd求最短路 - AcWing题库

#include <stdio.h>
#define N 210
#define MIN(a,b) ((a)<(b)?(a):(b))
int dist[N][N];
int main()
{int n,m,k,a,b,c;scanf("%d %d %d",&n,&m,&k);for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){if (i==j){dist[i][j]=0;}else{dist[i][j]=0x3f3f3f3f;}}}while(m--){scanf("%d %d %d",&a,&b,&c);dist[a][b]=MIN(dist[a][b],c);}for (int k=1;k<=n;k++){for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){dist[i][j]=MIN(dist[i][j],dist[i][k]+dist[k][j]);}}}while(k--){scanf("%d %d",&a,&b);if(dist[a][b]>0x3f3f3f3f/2){printf("impossible\n");}else{printf("%d\n",dist[a][b]);}}return 0;
}相关文章:

(算法基础)Floyd算法
适用情景Floyd算法适用于多源汇最短路,也就是他问你比如说从3号点到6号点的最短路距离,比如说从7号点到20号点的最短路距离,而不是单源最短路(从1号点到n号点的最短路距离)。在这个算法当中允许负权边的存在。但在求最…...

SQL语法:浅析select之七大子句
Mysql版本:8.0.26 可视化客户端:sql yog 目录一、七大子句顺序二、演示2.1 from语句2.2 on子句2.3 where子句2.4 group by子句2.4.1 WITHROLLUP,加在group by后面2.4.2 是否可以按照多个字段分组统计?2.4.3 分组统计时,…...

中国人民大学与加拿大女王大学金融硕士——去有光的地方,并成为自己的光
光是我们日常生活中一个重要的元素,试想一下如果没有光,世界将陷入一片昏暗。人生路亦是如此,我们从追逐光、靠近光、直到自己成为光。人民大学与加拿大女王大学金融硕士项目是你人生路上的一束光吗 渴望想要成为一个更好的人,就…...

Python数据结构与算法篇(五)-- 二分查找与二分答案
1 二分法介绍 1.1 定义 二分查找又称折半查找、二分搜索、折半搜索等,是一种在静态查找表中查找特定元素的算法。 所谓静态查找表,即只能对表内的元素做查找和读取操作,不允许插入或删除元素。 使用二分查找算法,必须保证查找表中…...
小游戏也要讲信用
当下,小游戏鱼龙混杂,官方为能更好地保护用户、开发者以及平台的权益,近日宣布7月1日起试行小游戏主体信用分机制。 主体信用分是什么呢?简单来说,这是针对小游戏主体下所有小游戏帐号行为,对开发者进行评…...

贪心算法11
1. 贪心算法的概念 所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。 贪心算法没有固定的算法框架,算法设计的关键是贪心…...
【并发编程】JUC并发编程(彻底搞懂JUC)
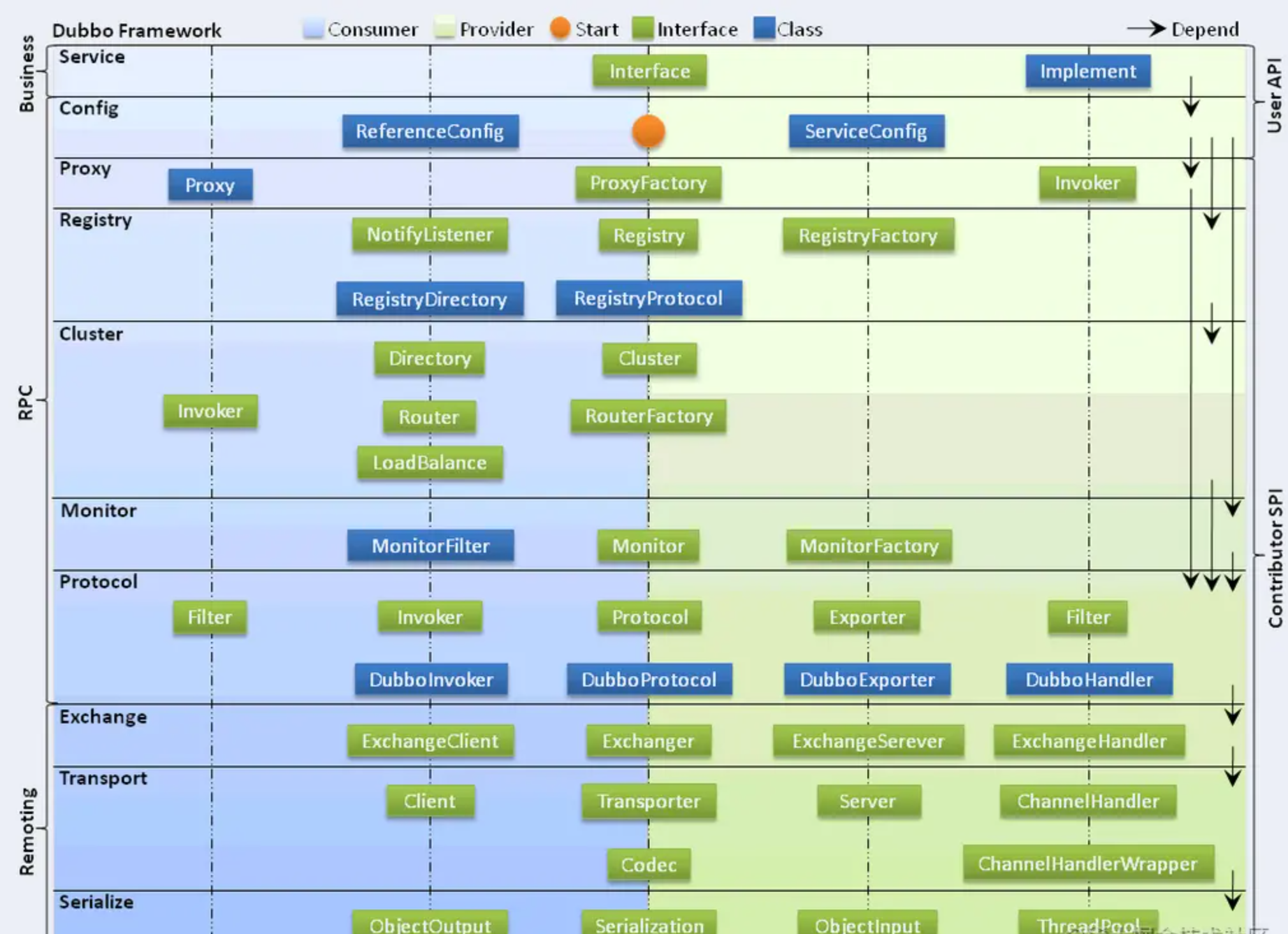
文章目录一、背景二、什么是JUC?三、JUC框架结构四、JUC框架概述五、JUC中常用类汇总六、相关名词进程和线程进程线程创建线程的几种常见的方式并发和并行用户线程和守护线程七、synchronized 作用范围:八、Lock锁(重点)什么是 Lock锁类型Lock接口lock()…...

Compose 动画 (七) : 高可定制性的动画 Animatable
1. Animatable和animateDpAsState的区别是什么 Animatable是Android Compose动画的底层API,如果我们查看源码,可以发现animateDpAsState内部是调用的animateValueAsState,而animateValueAsState内部调用的是Animatable animateDpAsState比A…...

vue3组件传值
1.父向子传值 父组件 引入子组件 import Son from ./components/Son.vue 设置响应式数据 const num ref(99) 绑定到子组件 <Son :num"num"></Son> 子组件 引入defineProps import { defineProps } from vue; 生成实例接收数据 type设置接收类…...

小白开发微信小程序00--文章目录
一个小白,一个老牛,空手能不能套白羊,能不能白嫖?我告诉你,一切都so easy,这个系列从0到106,屌到上天,盖过任何一个,试问,网上讲微信小程序开发的,…...
随手记录第九话 -- Java框架整合篇
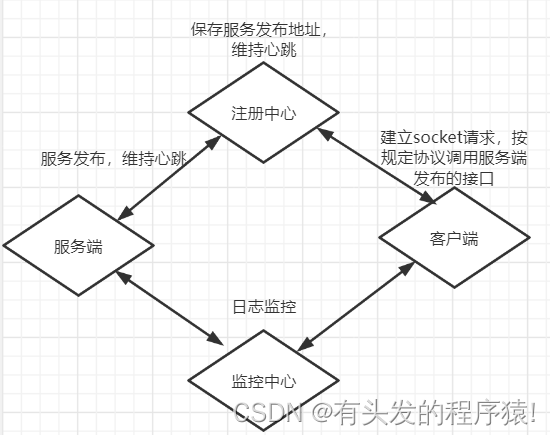
框架莫过于Spring了,那就以它为起点吧。 本文只为整理复习用,详细内容自行翻看以前文章。 1.Spring 有人说是Spring成就Java,其实也不是并无道理。 1.1 Spring之IOC控制反转 以XML注入bean的方式为入口,定位、加载、注册&…...
电影《铃芽之旅》观后感
这周看了电影《铃芽之旅》,整部电影是新海诚的新作。电影讲述的是女主铃芽为了关闭往门,在日本旅行中,遭遇灾难的故事。 (1)往昔记忆-往昔之物 电影中,有很多的“往门”,换成中国的话说…...
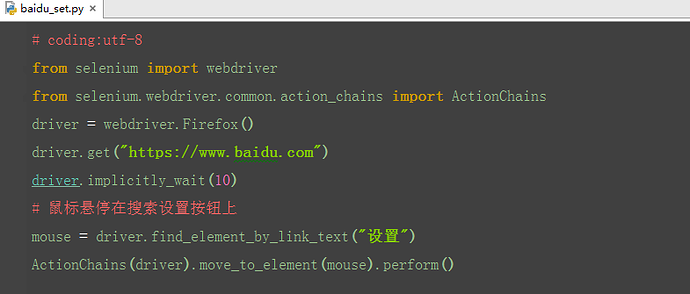
Web自动化测试(二)(全网最给力自动化教程)
欢迎您来阅读和练手!您将会从本章的详细讲解中,获取很大的收获!开始学习吧! 2.4 CSS定位2.5 SeleniumBuilder辅助定位元素2.6 操作元素(键盘和鼠标事件) 正文 2.4 CSS定位 前言 大部分人在使用selenium定…...

【C语言经典例题!】逆序字符串
目录 一、题目要求 二、解题步骤 ①递归解法 思路 完整代码 ②循环解法 思路 完整代码 嗨大家好! 本篇博客中的这道例题,是我自己在一次考试中写错的一道题 这篇博客包含了这道题的几种解法,以及一些我自己对这道题的看法ÿ…...

21 - 二叉树(三)
文章目录1. 二叉树的镜像2. 判断是不是完全二叉树3. 完全二叉树的节点个数4. 判断是不是平衡二叉树1. 二叉树的镜像 #include <ctime> class Solution {public:TreeNode* Mirror(TreeNode* pRoot) {// write code hereif (pRoot nullptr) return pRoot;//这里记得要记得…...

【A-Star算法】【学习笔记】【附GitHub一个示例代码】
文章目录一、算法简介二、应用场景三、示例代码Reference本文暂学习四方向搜索,一、算法简介 一个比较经典的路径规划的算法 相关路径搜索算法: 广度优先遍历(BFC)深度优先遍历(DFC)Di jkstra算法&#…...

纽扣电池澳大利亚认证的更新要求
澳大利亚强制性安全和信息标准草案具体规定了对含有纽扣电池和纽扣电池以 及纽扣电池和纽扣电池本身的消费品的要求, 适用范围 1.本法规适用于: 纽扣锂电池(任何尺寸和类型); 直径为16毫米或以上的纽扣锂电池: 一起提供的纽扣电池(未预先安装在产品中)。 2.但是&…...

零代码零距离,明道云开放日北京站圆满结束
文/麦壁瑜 编辑/李雨珂 2023年3月17日,为期一天的明道云开放日北京站圆满结束。本次开放日迎来超过100名伙伴和客户现场参会,其中不乏安利、通用技术集团、民生银行、迈外迪、DELSK集团、中国人民养老保险、北京汽车等知名企业代表。北京大兴机场、作业…...
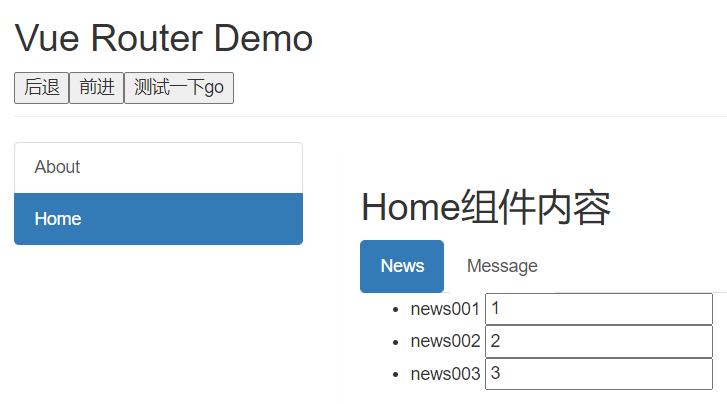
第五章Vue路由
文章目录相关理解vue-router的理解对SPA应用的理解路由的理解基本路由几个注意点嵌套路由——多级路由路由query参数命名路由路由的params参数路由的props配置路由跳转的replace方法编程式路由导航缓存路由组件路由组件独有的生命钩子activated和deactivated路由守卫全局路由守…...
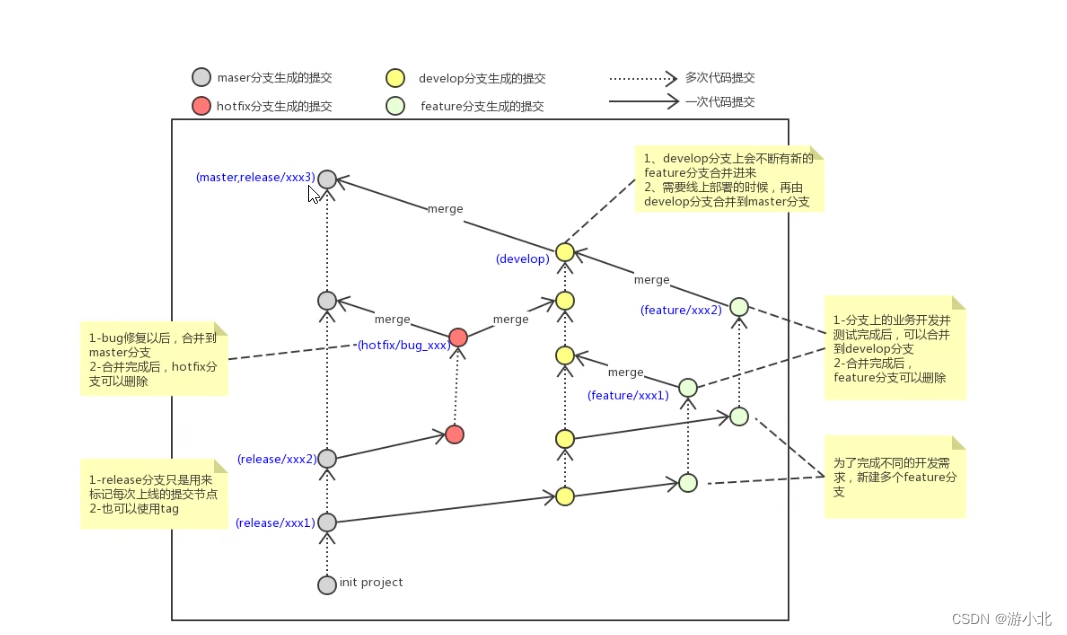
Git常用指令
Git是什么: Git是分布式版本控制系统(Distributed Version Control System,简称 DVCS),分为两种类型的仓库: 本地仓库和远程仓库 第一步先新建仓库,本地 init ,然后提交分枝 链接仓库…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
