第二十五章 添加数字签名
文章目录
- 第二十五章 添加数字签名
- 数字签名概述
- 添加数字签名
第二十五章 添加数字签名
本主题介绍如何向 IRIS Web 服务和 Web 客户端发送的 SOAP 消息添加数字签名。
通常,会同时执行加密和签名。为简单起见,本主题仅介绍签名。有关结合加密和签名的信息,请参阅主题结合加密和签名。
主题使用派生密钥令牌进行加密和签名描述了向 SOAP 消息添加数字签名的另一种方法。
数字签名概述
可以使用数字签名来检测消息是否被篡改,或者简单地验证消息的某一部分是否确实由所列实体生成。与传统的手工签名一样,数字签名是对文档的附加,只有文档的创建者才能创建,并且不容易伪造。
IRIS 对 SOAP 消息的数字签名的支持基于 WS-Security 1.1。反过来,WS-Security 遵循 XML 签名规范。根据后者的规范,要对 XML 文档进行签名:
- 使用摘要函数来计算文档一个或多个部分的哈希值。
- 将摘要值连接起来。
- 使用私钥加密串联摘要。(这是只有才能执行的计算。)
- 创建
<Signature>元素,其中包含以下信息:
- 对已签名部分的引用(以表明该签名适用于消息的哪些部分)。
- 加密的摘要值。
- 使接收者能够识别用于解密加密摘要值的公钥的信息。
此信息可以包含在<Signature>元素中,或者 <Signature> 元素可以包含对包含 X.509 证书或签名的 SAML 断言的二进制安全令牌的直接引用。在后一种情况下,必须在添加 <Signature>元素之前将安全令牌添加到消息中。
此信息还可以让收件人验证您是公钥/私钥对的所有者。
使用派生密钥令牌进行加密和签名主题介绍了一种向 SOAP 消息添加数字签名的替代方法。消息本身的细节各不相同,但一般过程是相同的,并遵循 XML 签名规范:生成签名部分的摘要,加密摘要,并包含一个 <Signature> 元素,其中包含使收件人能够验证签名和解密加密摘要的信息。
添加数字签名
要对 SOAP 消息进行数字签名,可以使用此处的基本过程或本主题后续部分中描述的变体。
首先,下图概括了这个过程:

具体过程如下:
- 可选择包含
%soap.inc包含文件,它定义了可能需要使用的宏。 - 如果要对任何安全标头元素进行签名,请创建这些安全标头元素。例如:
set utoken=##class(%SOAP.Security.UsernameToken).Create("_SYSTEM","SYS")
- 创建
%SYS.X509Credentials实例,如以编程方式检索凭证集中所述。此 IRIS 凭证集必须包含自己的证书,并且必须提供私钥密码(如果尚未加载)。例如:
Set x509alias = "servercred" Set pwd = "mypassword" Set credset = ##class(%SYS.X509Credentials).GetByAlias(x509alias,mypassword)
- 创建包含与该凭证集关联的证书的二进制安全令牌。为此,调用
%SOAP.Security.BinarySecurityTokenO的CreateX509Token()类方法。例如:
set bst=##class(%SOAP.Security.BinarySecurityToken).CreateX509Token(credset)
此方法返回代表 <BinarySecurityToken> 标头元素的 %SOAP.Security.BinarySecurityToken实例。
- 将此令牌添加到
WS-Security标头元素。为此,请调用Web客户端或Web服务的SecurityOut属性的AddSecurityElement()方法。对于方法参数,请使用刚刚创建的令牌。例如:
do ..SecurityOut.AddSecurityElement(bst)
- 根据二进制安全令牌创建
<Signature>元素。为此,调用%XML.Security.Signature的 CreateX509()类方法。例如:
set dsig=##class(%XML.Security.Signature).CreateX509(bst)
此方法返回 %XML.Security.Signature 的实例,该实例表示 &<Signature>标头元素。<Signature> 元素适用于消息的一组默认部分;可以指定一组不同的部分。
正式地,该方法具有以下签名:
classmethod CreateX509(credentials As %SYS.X509Credentials = "", signatureOptions As %Integer, referenceOption As %Integer, Output status As %Status) as %XML.Security.Signature
credentials- 凭据要么是实例中的%SYS.X509Credentials,要么是实例中的%SAML.Assertion,要么是实例中的%SOAP.Security.BinarySecurityToken。signatureOptions指定要签名的部分。此选项在将数字签名应用于特定消息部分中进行了描述。referenceOption指定要创建的引用类型。有关详细信息,请参阅X.509凭证的引用选项。status表示该方法是否成功。
- 将数字签名添加到
WS-Security标头元素。为此,请调用Web客户端或Web服务的SecurityOut属性的AddSecurityElement()方法。对于参数,请指定上一步中创建的签名对象。例如:
do ..SecurityOut.AddSecurityElement(dsig)
- 发送
SOAP消息。请参阅添加安全标头元素中的一般注释。
相关文章:

第二十五章 添加数字签名
文章目录 第二十五章 添加数字签名数字签名概述添加数字签名 第二十五章 添加数字签名 本主题介绍如何向 IRIS Web 服务和 Web 客户端发送的 SOAP 消息添加数字签名。 通常,会同时执行加密和签名。为简单起见,本主题仅介绍签名。有关结合加密和签名的信…...

GHOST重装后DEF盘数据救援指南
一、现象解析:GHOST重装后的DEF盘失踪之谜 在计算机维护的日常中,GHOST重装因其快速便捷的特点,成为众多用户解决系统问题的首选方法。然而,这一操作虽能迅速恢复系统至初始状态,却也暗藏风险,尤其是当不慎…...

使用blender快速制作metahuman面部以及身体绑定教程
【metablriger教程】使用blender一键绑定自定义角色metahuman绑定并导入UE5引擎教程_哔哩哔哩_bilibili 目前市面上的制作metahuman绑定的工具大多是maya的,metablriger是一个帮助用户快速制作metahuman绑定的blender插件,可以平替市面上已有的metahuma…...
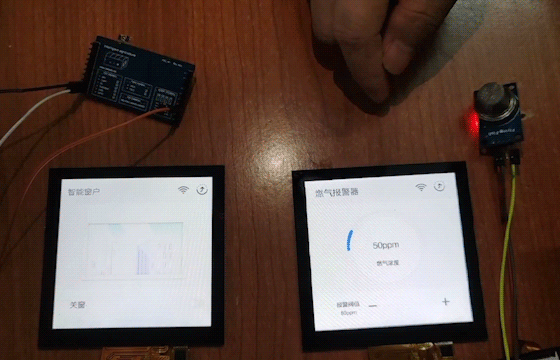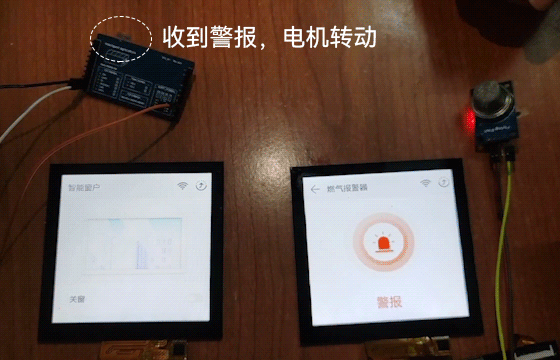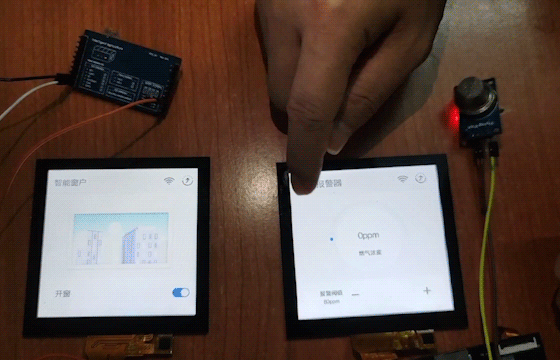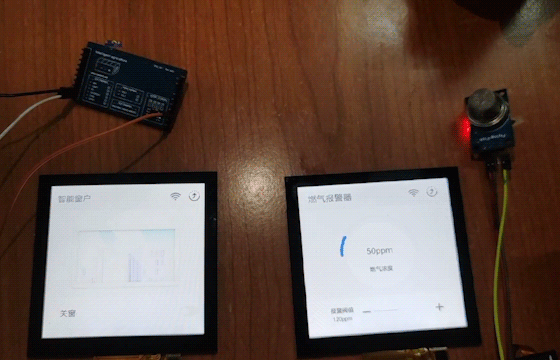
OpenHarmony鸿蒙( Beta5.0)智能窗户通风设备开发详解
鸿蒙开发往期必看: 一分钟了解”纯血版!鸿蒙HarmonyOS Next应用开发! “非常详细的” 鸿蒙HarmonyOS Next应用开发学习路线!(从零基础入门到精通) “一杯冰美式的时间” 了解鸿蒙HarmonyOS Next应用开发路…...

pandas 将多条记录整合成一条记录,每条记录的year和month字段组成新的字段名
你可以使用 Pandas 的 pivot_table() 或 groupby() 方法,将多条记录整合成一条,并通过 year 和 month 这两个字段生成新的字段名。具体的实现方法是通过 pivot_table() 将 year 和 month 作为列标签,将其他列中的数据进行整合。 假设你的数据…...

C# 中的多线程同步:原子变量、原子操作、内存顺序和可见性
C# 中的多线程同步:原子变量、原子操作、内存顺序和可见性 引言 随着现代计算机系统的发展,多核处理器已经变得非常普遍。在这种环境下,多线程编程成为提高应用程序性能的关键技术之一。然而,多线程编程带来了新的挑战ÿ…...

视图(mysql)
一、什么是视图 视图是⼀个虚拟的表,它是基于⼀个或多个基本表或其他视图的查询结果集。视图本⾝不存储数 据,⽽是通过执⾏查询来动态⽣成数据。⽤⼾可以像操作普通表⼀样使⽤视图进⾏查询、更新和管 理。视图本⾝并不占⽤物理存储空间,它仅…...

elementui组件el-upload实现批量文件上传
el-upload组件上传文件时,每传一个文件会调一次接口,所以当上传多个文件的时候,有 n 个文件就要调 n 次接口。 刚好之前工作中遇到使用el-upload组件批量上传文件的需求,来看看怎么实现。 思路: 1.取消组件的自动上…...

【JAVA入门】Day45 - 压缩流 / 解压缩流
【JAVA入门】Day45 - 压缩流 / 解压缩流 文章目录 【JAVA入门】Day45 - 压缩流 / 解压缩流一、解压缩流二、压缩流 在文件传输过程中,文件体积比较大,传输较慢,因此我们发明了一种方法,把文件里的数据压缩到一种压缩文件中&#x…...

Qt_自定义信号
目录 1、自定义信号的规定 2、创建自定义信号 3、带参数的信号与槽 4、一个信号连接多个槽 5、信号与槽的断开 结语 前言: 虽然Qt已经内置了大量的信号,并且这些信号能够满足大部分的开发场景,但是Qt仍然允许开发者自定义信号&#…...
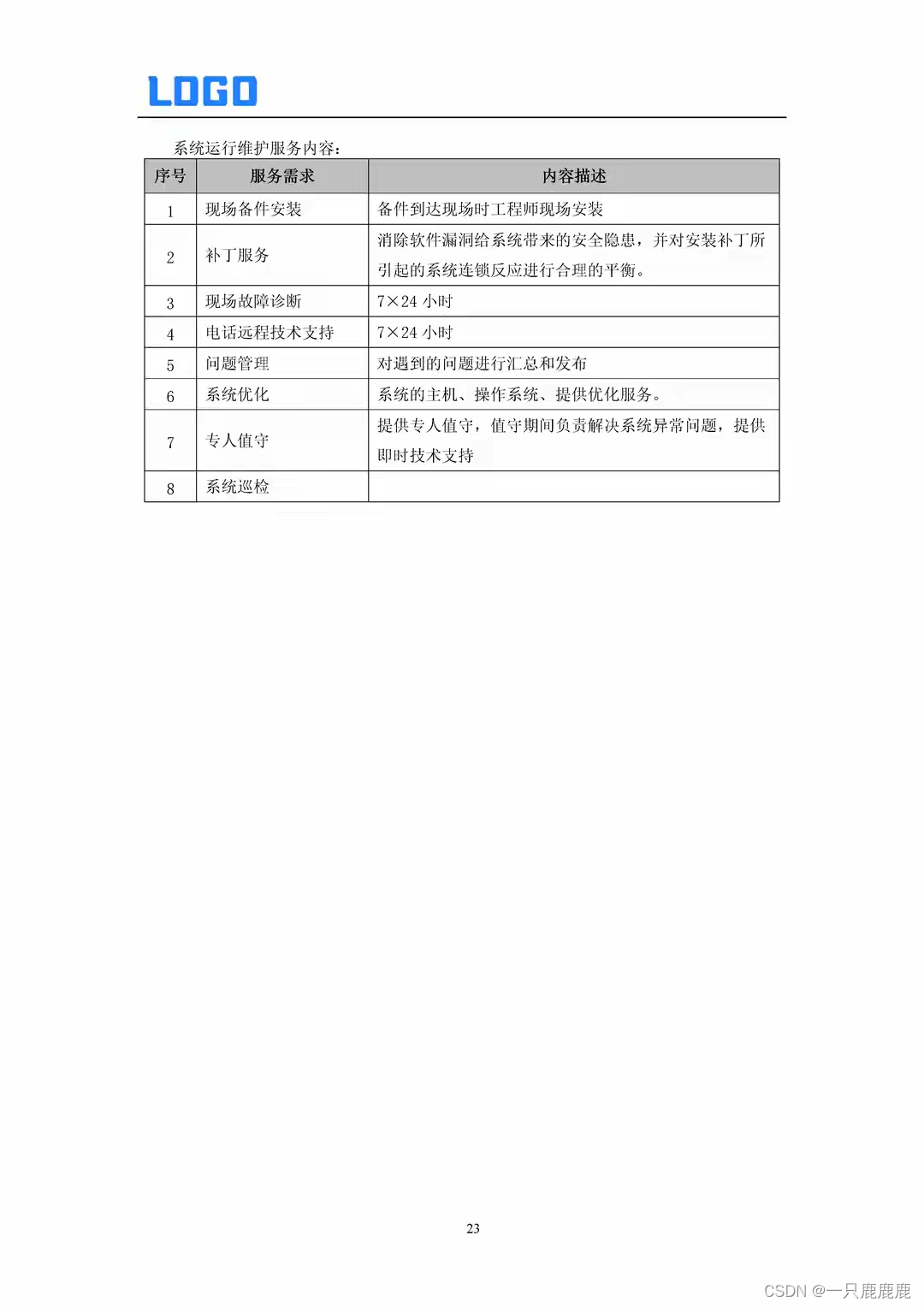
【运维方案】某系统运维需求方案参考(doc全原件2024)
系统运维需求方案 1服务目标 2服务人力需求、服务资源需求 3信息资产统计服务需求 4业务应用软件服务需求 5网络、安全系统运维服务需求 6主机、存储系统运维服务需求 7数据库系统运维服务需求 8终端运维服务需求 9综合布线系统服务需求 10大屏幕显示系统的维护需求 11视频会议…...

Linux环境使用Git同步教程
📖 前言:由于CentOS 7已于2024年06月30日停止维护,为了避免操作系统停止维护带来的影响,我们将把系统更换为Ubuntu并迁移数据,在此之前简要的学习Git的上传下载操作。 目录 🕒 1. 连接🕘 1.1 配…...

c++临时对象导致的生命周期问题
对象的生命周期是c中非常重要的概念,它直接决定了你的程序是否正确以及是否存在安全问题。 今天要说的临时变量导致的生命周期问题是非常常见的,很多时候没有一定经验甚至没法识别出来。光是我自己写、review、回答别人的问题就犯了或者看到了许许多多这…...

CSP-J 算法基础 深度优先搜索
文章目录 前言深度优先搜索通俗解释例子深度优先搜索的步骤DFS 的特点生活中的类比 为什么递归问题会变成深度优先搜索?递归与深度优先搜索的关系:递归与系统栈递归调用的过程:栈的作用: 递归与系统栈的简单示例递归实现 DFS 的简…...

LeetCode题练习与总结:基本计算器 Ⅱ--227
一、题目描述 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-2^31, 2^31 - 1] 的范围内。 注意:不允许使用任何将字符串作为数学表达式计算…...

Elasticsearch基础(七):Logstash如何开启死信队列
文章目录 Logstash如何开启死信队列 一、确保 Elasticsearch 输出插件启用 DLQ 支持 二、配置 Logstash DLQ 设置 三、查看死信队列 四、排查 CSV 到 Elasticsearch 数据量不一致的问题 Logstash如何开启死信队列 在 Logstash 中,死信队列(Dead Le…...
讲解)
c语言--力扣简单题目(链表的中间节点)讲解
题目如下: 给你单链表的头结点 head ,请你找出并返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。 示例 1: 输入:head [1,2,3,4,5] 输出:[3,4,5] 解释:链表只有一个中间结点…...

【STM32 Blue Pill编程】-定时器计数模式
定时器计数模式 文章目录 定时器计数模式1、定时器计数模式介绍2、硬件准备及接线3、模块配置3.1 定时器计数模式配置3.2 定时器中断配置3.3 串口配置4、代码实现在本文中,我们将讨论如何在计数器模式下配置 STM32 Blue Pill 定时器模块。 要将定时器用作计数器,我们将其配置…...

【例题】lanqiao1331 二进制中 1 的个数
二进制中 1 的个数 题目描述 给定一个整数 x,输出该数二进制表示中 1 的个数。 例:9 的二进制表示为 1001,有 2 位是 1 ,所以函数返回 2。 输入描述 输入 x (内存空间为 32 位的整数)。 输出描述 第一…...

【论文解读】图像序列识别:CRNN技术在场景文本识别中的应用与突破(附论文地址)
论文地址:https://arxiv.org/pdf/1507.05717 这篇文章的标题是《An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition》,作者是Baoguang Shi, Xiang Bai和Cong Yao,…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
