混合整数规划及其MATLAB实现
目录
引言
混合整数规划的基本模型
混合整数规划的求解方法
MATLAB中的混合整数规划实现
示例:多变量系统的混合整数规划
表格总结:混合整数规划的求解方法与适用场景
结论
引言
混合整数规划(Mixed Integer Programming, MIP)是优化领域中一种重要的分支,它结合了连续变量和整数变量的优化问题。在实际应用中,很多优化问题既包含需要连续取值的变量(如资源分配问题中的数量或时间),也包含只能取整数或二元变量的情况(如设施选址问题中的决策是否选址)。这种问题的复杂性较高,求解时需要同时处理线性、非线性和整数约束。混合整数规划广泛应用于生产计划、物流运输、能源系统设计等领域。
随着求解技术的不断发展,像MATLAB这样的计算工具为解决混合整数规划问题提供了强大的支持。MATLAB的优化工具箱中集成了多种求解器,可以高效处理带有整数和连续变量的混合整数规划问题。本文将介绍混合整数规划的理论基础、常见的求解方法,并结合MATLAB给出具体的实现与分析。
混合整数规划的基本模型
混合整数规划问题的标准形式可以表示为:

混合整数规划模型的核心在于处理整数变量与连续变量的混合,这往往增加了问题的复杂性和求解难度。与纯整数规划或线性规划不同,MIP问题的解空间较大,需要使用特殊的优化算法,如分支定界法(Branch and Bound)、割平面法(Cutting Plane)等。
混合整数规划的求解方法
-
分支定界法(Branch and Bound): 分支定界法是解决MIP问题的经典算法。其基本思想是通过递归划分解空间,逐步缩小搜索范围。在每一步中,先对变量进行连续松弛,得到子问题的解,然后根据该解将问题分为不同的分支,并递归处理每个分支。
-
割平面法(Cutting Plane): 割平面法通过引入新的约束来切割解空间,从而消除不符合整数约束的解。这些新的约束称为“割平面”,可以帮助快速逼近最优解。
-
内点法(Interior Point Method): 内点法是一种用于求解大规模线性规划和混合整数规划问题的算法。它通过从解空间的内部逐步逼近最优解,适用于处理带有较多连续变量的问题。
-
启发式算法: 对于大规模的MIP问题,精确算法的求解时间可能会很长,启发式算法(如遗传算法、模拟退火等)可以在合理的时间内找到近似解。虽然这些算法不能保证全局最优解,但可以在求解速度上提供显著优势。
MATLAB中的混合整数规划实现
MATLAB 提供了 intlinprog 函数用于求解带有整数约束的线性规划问题。此外,还可以使用 OPTI 工具箱处理更加复杂的混合整数规划问题,尤其是涉及非线性目标函数或约束条件的情况。
示例:多变量系统的混合整数规划
我们考虑一个典型的混合整数规划问题,其中需要最大化某种效用函数,且约束条件包括多个整数和连续变量。该问题可以通过以下MATLAB代码求解。
代码示例
function main% 定义目标函数fun = @obj;% 定义不等式约束 nlcon(x) nlcon = @cons;cl = [1; 1; 1; 0; 0; 0; 20; 40]; % 约束下界cu = [Inf; Inf; Inf; 0.5; 0.5; 0.5; 20; 40]; % 约束上界% 变量的上下界lb = zeros(12,1);ub = [20; 20; 40; 40; 20; 20; 40; 40; 20; 20; 40; 40];% 初始解猜测x0 = [1 1 1 1 1 1 1 1 1 1 1 1]';% 设置求解器选项opts = optiset('display', 'iter');% 变量类型定义 C表示连续变量,I表示整数变量xtype = 'CCIICCIICCII';% 构造求解对象Opt = opti('fun', fun, 'nl', nlcon, cl, cu, 'bounds', lb, ub, 'x0', x0, 'xtype', xtype, 'options', opts);% 求解问题[x, fval, exitflag, info] = solve(Opt);% 输出结果disp(['最优解: ', num2str(x)]);disp(['目标函数值: ', num2str(fval)]);
end% 目标函数
function o = obj(x)o = -3*(x(3)/20)*log2(1+5*x(1)/x(3)) - 3*(x(4)/20)*log2(1+5*x(2)/x(4)) - ...3*(x(7)/20)*log2(1+10*x(5)/x(7)) - 3*(x(8)/20)*log2(1+10*x(6)/x(8)) - ...3*(x(11)/20)*log2(1+15*x(9)/x(11)) - 3*(x(12)/20)*log2(1+15*x(10)/x(12));
end% 非线性约束条件
function con = cons(x)con(1) = x(3)*0.25*log2(1 + (5*x(1))/(x(3)));con(2) = x(7)*0.25*log2(1 + (10*x(5))/(x(7)));con(3) = x(11)*0.25*log2(1 + (15*x(9))/(x(11)));con(4) = exp(-125*(x(4)*0.25*log2(1 + (5*x(2))/(x(4))) - 1)*0.5); con(5) = exp(-125*(x(8)*0.25*log2(1 + (10*x(6))/(x(8))) - 1)*0.5);con(6) = exp(-125*(x(12)*0.25*log2(1 + (15*x(10))/(x(12))) - 1)*0.5);con(7) = x(1) + x(2) + x(5) + x(6) + x(9) + x(10);con(8) = x(3) + x(4) + x(7) + x(8) + x(11) + x(12);
end
表格总结:混合整数规划的求解方法与适用场景
| 方法 | 描述 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 分支定界法 | 通过分解问题并缩小搜索空间来求解MIP问题 | 能有效处理大规模整数规划问题,保证全局最优 | 计算时间较长,尤其是变量规模较大时 | 大规模MIP问题,包含复杂的整数约束 |
| 割平面法 | 引入割平面约束,切割掉不符合整数约束的解 | 能快速减少解空间,提高求解速度 | 对于非凸问题效果不佳 | 有大量连续变量且需要逼近整数解的优化问题 |
| 内点法 | 从解空间内部逐步逼近最优解 | 适用于处理大规模线性和非线性问题 | 可能陷入局部最优解,需要结合其他算法进行优化 | 大规模连续变量优化问题,如生产计划和资源分配 |
| 启发式算法 | 基于随机搜索和进化策略的近似求解算法 | 计算速度快,适用于难以求解的复杂问题 | 无法保证全局最优解,仅能提供近似解 | 大规模复杂优化问题,如网络规划和路径优化 |
结论
混合整数规划作为一种结合连续变量和整数变量的优化方法,能够高效解决生产计划、物流、能源系统设计等领域中的复杂问题。通过分支定界法、内点法等算法,MATLAB中的 intlinprog 和 OPTI 工具箱可以有效处理这类问题,帮助决策者在实际应用中找到最优解。

相关文章:

混合整数规划及其MATLAB实现
目录 引言 混合整数规划的基本模型 混合整数规划的求解方法 MATLAB中的混合整数规划实现 示例:多变量系统的混合整数规划 表格总结:混合整数规划的求解方法与适用场景 结论 引言 混合整数规划(Mixed Integer Programming, MIP…...

【数据结构】6——图1,概念
数据结构6——图1,概念 文章目录 数据结构6——图1,概念基本概念图的分类图的表示方法 基本概念 由 顶点(Vertex) 和 边(Edge) 组成的集合。顶点表示图中的点,而边表示顶点之间的连接。记为 G …...
)
技术周总结 09.09~09.15周日(C# WinForm WPF)
文章目录 一、09.09 周一1.1) 问题01: Windows桌面开发中,WPF和WinForm的区别和联系?联系:区别: 二、09.12 周四2.1)问题01:visual studio的相关快捷键有哪些?通用快捷键编辑导航调试窗口管理 2…...
4K投影仪选购全攻略:全玻璃镜头的当贝F6,画面细节纤毫毕现
在当今的投影市场上,4K投影仪已经成了主流产品,越来越多家庭开始关注如何选择一款性价比高、口碑好的4K投影仪。4K投影仪其实指的是具备3840*2160像素分辨率投影仪,它能够提供更清晰、更细腻、更真实的画面效果。 那么4K投影仪该怎么选&…...

除了字符串前导的*号之外,将串中其它*号全部删除
要求 假定输入的字符串中只包含字母和*号。请编写函数fun,它的功能是:除了字符串前导的*号之外,将串中其它*号全部删除。在编写函数时,不得使用C语言提供的字符串函数。函数fun中给出的语句仅供参考。 例如,字符串中的内容为:-**…...

SpringBoot开发——使用@Slf4j注解实现日志输出
文章目录 1、Lombok简介2、SLF4J简介3、实现步骤3.1 创建SpringBoot项目3.2 添加依赖3.3 使用 Slf4j 注解3.4 输出日志信息 4、结论 在现代Java开发中,日志记录是至关重要的。它不仅帮助开发者调试代码,还便于监控系统运行状态和性能。 Lombok 和 SLF4J …...

VSCode拉取远程项目
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

【已解决】SpringBoot3项目整合Druid依赖:Druid监控页面404报错
文章标题 问题描述原因分析解决方案参考资料 问题描述 最近,笔者在SpringBoot3项目中整合Druid连接池时,偶然翻到一条介绍Druid监控的短视频,兴致盎然之下尝试设置了一下Druid监控。 But,按照视频中提供的yml参数对照设置&#x…...

【算法】滑动窗口—找所有字母异位词
“找到字符串中所有字母异位词”的难度为Medium,看一下题目: 给定一个字符串 S 和一个非空字符串 T,找到 S 中所有是 T 的字母异位词的子串,返回这些子串的起始索引。 所谓的字母异位词,其实就是全排列,原题…...

Vue安装及环境配置【图解版】
欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 Facts speak louder than words! 目录 一.node.js的安装…...

绕过CDN查找真实IP方法
1、前言 在新型涉网案件中,我们在搜集到目标主站之后常常需要获取对方网站的真实IP去进一步的信息搜集,但是现在网站大多都部署了CDN,将资源部署分发到边缘服务器 实现均衡负载,降低网络堵塞,让用户能够更快地访问自己…...

Qt与MQTT交互通信
MQTT全称是(Message Queuing Telemetry Transport),即消息队列遥测传输协议 是一种基于发布/订阅(Publish/Subscribe)模式的轻量级通讯协议,并且该协议构建于TCP/IP协议之上,常用于互联网中&am…...

dd 命令:复制和转换文件
一、dd 命令简介 dd 命令是一个在 Unix 和类 Unix 系统中用于复制文件和转换文件的命令行工具。它的功能非常强大,可以用于各种目的,例如创建镜像文件、备份和恢复数据、复制数据等。 dd 是一个用于读取、转换和写入数据的工具,通常…...

文件系统(磁盘 磁盘文件 inode)
文章目录 磁盘看看物理磁盘磁盘的存储结构 对磁盘的储存进行逻辑抽象inode号文件名 -> inode判断文件在哪个分区 磁盘 电脑中存在非常多的文件,被打开的文件只是少量的。 没有被打开的文件,在磁盘中放着,那么文件是如何存取? …...

ThreeJs创建圆环
ThreeJs除了创建基本的长方体,球形,圆柱等几何体,也可以创建一些特殊的几何体,比如圆环,多边体,这节就来讲怎么用Threejs绘制出圆环。首先依然是要创建出基础的组件,包括场景,相机&a…...

React实现类似Vue的路由监听Hook
React实现类似Vue的路由监听Hook 监听路由变化;React Hook封装,返回回调函数,新旧路由为函数参数; 代码 import { useEffect, useRef } from react; import { useHistory, useLocation } from react-router-dom;/*** 监听路由变…...

Visual Studio打开项目的一些小技巧
Visual Studio(VS)是一款功能强大的集成开发环境,许多刚入门C/C的小白也会使用这款软件进行写代码,然而它的操作并不简单,下面将讲解一下VS打开项目文件的一些小技巧。 目录 🎁创建空项目 ❤️①点击“创建新项目” ❤️②点击“…...

前端页面中使用 ppt 功能,并且可以随意插入关键帧
要在前端页面中实现类似 PowerPoint 的功能,并且能够随意插入和控制关键帧动画,你可以使用 HTML、CSS 和 JavaScript 结合的方式来创建一个互动幻灯片系统。以下是一个详细的实现方案,包括如何插入和控制关键帧动画: 1. 基础 HTM…...

机器学习:opencv--图像金字塔
目录 一、图像金字塔 1.图像金字塔是什么? 2.有哪些常见类型? 3.金字塔的构建过程 4.图像金字塔的作用 二、图像金字塔中的操作 1.向下采样 2.向上采样 3.注意--无法复原 三、代码实现 1.高斯金字塔向下采样 2.高斯金字塔向上采样 3.无法复…...

linux安全软件Hydra使用教程
Hydra 是一个强大的网络登录工具,常用于渗透测试,支持对多种服务和协议(如 SSH、FTP、HTTP 等)进行暴力crack攻击。它可以通过字典攻击来测试用户名和密码的有效性。以下是关于如何使用 Hydra 的基本步骤和示例: 1. 安…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
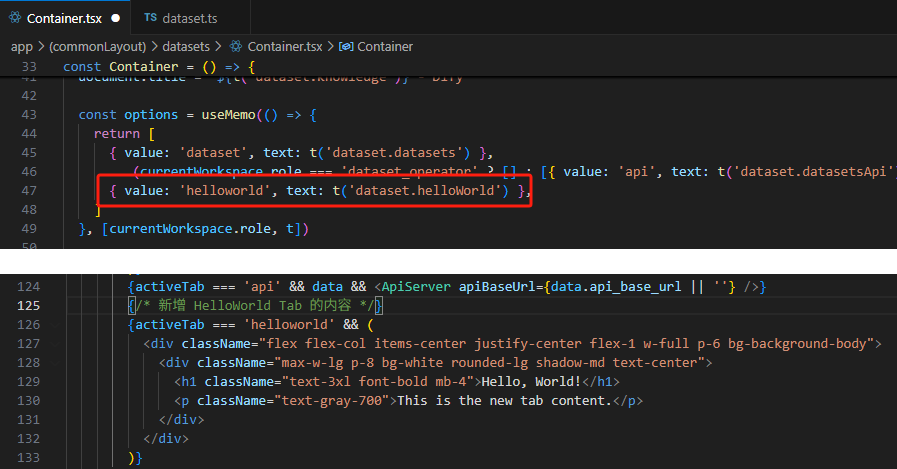
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...
