数据结构中线性表的定义和特点
线性表:有n个数据特征相同的元素构成的有限序列。
特点:
除了第一个元素,最后一个元素,其余的元素都有唯一的前驱和唯一的后继。
案例引入:
一元多项式的运算:
可以将一元多项式p(x)抽象为一个有n+1个系数组成的有序序列,该序列可以用线性表p表示。
Q(x)是一元m次多项式,也可以用线性表Q表示,再将两个多项式进行相加R(x)=P(x)+Q(x).可以用线性表R表示
稀疏多项式的运算
为了避免造成空间的浪费,数据元素可以包含多个数据项,对每一项可用(系数,指数)的形式唯一确定。
用一个长度为m每一个元素有两个数据项(系数项,指数项)的线性表
((p1,e1),(p2,e2),...(pm,em))便可以确定多项式p(x),在最坏的情况下,n+1(=m)个系数都不为0.
稀疏多项式的运算:指数相同:对应系数相加,若其和相加不为0,在c中增加一个新项。
指数不相同:则江直树较小的项复制到c中。
顺序存储结构缺点:存放空间分配不灵活
运算的空间结构复杂的,所以改进方法是用另一种链式存储。
图书系统管理:功能:
(1)查找 :查找有关图书的相关信息,返回图书在表中的位置序号。
(2)插入 :插入一个新的图书。
(3)删除 :删除一条图书的信息。
(4)修改 :修改该图书的价格。
(5)排序 :将图书的价格按照从高到低。
(6)计数 :统计图书的数量。
每个图书作为线性表中的元素,然后采用适当的存储结构来表示该线性表,这些问题中都包含n个数据特征相同的元素,既可以表示为线性表,但是不同的数据类型不尽相同,可以为简单数据类型,也可以为复杂的数据类型。
相关文章:

数据结构中线性表的定义和特点
线性表:有n个数据特征相同的元素构成的有限序列。 特点: 除了第一个元素,最后一个元素,其余的元素都有唯一的前驱和唯一的后继。 案例引入: 一元多项式的运算: 可以将一元多项式p(x)抽象为一个有n1个系…...
模块详解)
【PyTorch单点知识】PyTorch中的自动混合精度(AMP)模块详解
文章目录 0. 前言1. 什么是自动混合精度?2. PyTorch AMP 模块3. 如何使用 PyTorch AMP3.1 环境准备3.2 代码实例3.3 代码解析 4. 结论 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解及成果&a…...

数据结构 --- 哈希表
哈希表(Hash Table),也叫散列表,是一种根据关键码值(Key value)而直接进行访问的数据结构。 一、基本原理 哈希函数 哈希表通过一个特定的哈希函数,将关键码映射到表中的一个位置。这个位置通常…...

Linux相关:在阿里云下载centos系统镜像
文章目录 1、镜像站2、下载方式一2.1、第一步打开镜像站地址2.2 下载地址: https://mirrors.aliyun.com/centos/2.3、选择7版本2.4、镜像文件在isos文件夹中2.5、选择合适的版本 3、下载镜像快捷方式 1、镜像站 阿里云镜像站地址 2、下载方式一 2.1、第一步打开镜像站地址 2…...

24. 线模型对象
线模型Line渲染顶点数据 下面代码是把几何体作为线模型Line (opens new window)的参数,你会发现渲染效果是从第一个点开始到最后一个点,依次连成线。 // 线材质对象 const material new THREE.LineBasicMaterial({color: 0xff0000 //线条颜色 }); //…...

EasyExcel 快速入门
目录 一、 EasyExcel简介 官网链接: 代码链接: 二、 EasyExcel快速上手 引入依赖: 设置Excel相关注解 编写对应的监听类: 简单写入数据: 简单读取数据: 不需要使用监听器: 需要使…...

Sparse4D v1
Sparse4D: Multi-view 3D Object Detection with Sparse Spatial-Temporal Fusion Abstract 基于鸟瞰图 (BEV) 的方法最近在多视图 3D 检测任务方面取得了重大进展。与基于 BEV 的方法相比,基于稀疏的方法在性能上落后,但仍然有很多不可忽略的优点。为了…...

速盾:你知道高防 IP 和高防 CDN 的区别吗?
在当今网络安全形势日益严峻的情况下,网站的安全防护成为了企业和个人关注的焦点。高防 IP 和高防 CDN 作为两种常见的网络安全防护手段,被广泛应用于网站的安全防护中。那么,高防 IP 和高防 CDN 有什么区别呢?防护网站哪个更好呢…...

HTML和CSS网页制作成品
HTML和CSS网页制作成品 一、引言 1. 背景介绍 在当今数字化时代,网页已成为信息传递和交流的重要媒介。HTML和CSS作为网页制作的基石,对于构建美观、功能丰富的网站至关重要。本文将详细介绍如何使用HTML和CSS来制作一个网页成品。 2. 目的和重要性 …...

Ai+若依(集成easyexcel实现excel表格增强)
EasyExcel 介绍 官方地址:EasyExcel官方文档 - 基于Java的Excel处理工具 | Easy Excel 官网 Java解析、生成Excel比较有名的框架有Apache poi、jxl。但他们都存在一个严重的问题就是非常的耗内存,poi有一套SAX模式的API可以一定程度的解决一些内存溢出的问题,但POI还是有一…...
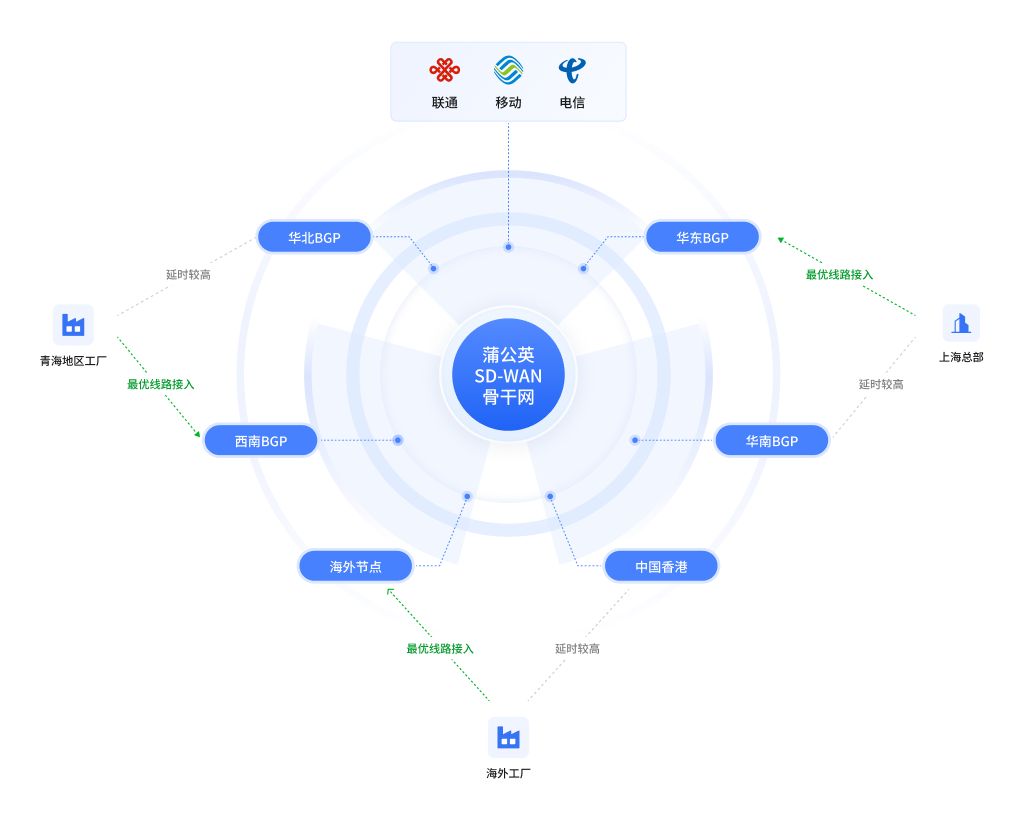
钻机、塔吊等大型工程设备,如何远程维护、实时采集运行数据?
在建筑和工程领域,重型设备的应用不可或缺,无论是在道路与桥梁建设、高层建筑施工,还是在风电、石油等能源项目的开发中,都会用到塔吊、钻机等大型机械工程设备。 随着数字化升级、工业4.0成为行业发展趋势,为了进一步…...

【AutoX.js】选择器 UiSelector - 查找包名
文章目录 原文:https://blog.c12th.cn/archives/38.html选择器 UiSelector - 查找包名笔记直接查找包名双层判断(推荐)查找最外层控件的子控件 最后 原文:https://blog.c12th.cn/archives/38.html 选择器 UiSelector - 查找包名 笔记 AutoX.js UiSelec…...

ERP进销存多仓库管理系统源码 带完整的安装代码包以及搭建部署教程
系统概述 ERP进销存多仓库管理系统是一款专为中小企业量身定制的集成化管理软件,它集成了采购管理、销售管理、库存管理、财务管理以及多仓库协同作业等核心模块。通过统一的平台,企业可以实时掌握商品从入库到出库的全过程,实现库存的自动化…...

数据清洗-缺失值填充-对XGBoost参数优化填充
目录 一、安装所需的python包二、采用XGboost算法进行缺失值填充2.1可直接运行代码2.2以某个缺失值数据进行实战2.2.1 代码运行过程截屏:2.2.2 填充后的数据截屏:三、网格搜索(Grid Search)对 XGBoost 模型的超参数进行优化原理介绍3.1 说明3.2 参数优化的原理1. 网格搜索(…...

Qt_按钮类控件
目录 1、QAbstractButton 2、设置带图标的按钮 3、设置带有快捷键的按钮 4、QRadioButtion(单选按钮) 4.1 QButtonGroup 5、QCheckBox 结语 前言: 按钮类控件是Qt中最重要的控件类型之一,该类型的控件可以通过鼠标的点击…...

union 的定义和基本结构以及用途
在 C 语言中,union(联合体) 是一种数据结构,它允许多个成员共享相同的内存空间。换句话说,联合体中的所有成员都存储在同一块内存区域,不同的成员会占用相同的内存地址,但在同一时刻只能保存一个…...

混合整数规划及其MATLAB实现
目录 引言 混合整数规划的基本模型 混合整数规划的求解方法 MATLAB中的混合整数规划实现 示例:多变量系统的混合整数规划 表格总结:混合整数规划的求解方法与适用场景 结论 引言 混合整数规划(Mixed Integer Programming, MIP…...

【数据结构】6——图1,概念
数据结构6——图1,概念 文章目录 数据结构6——图1,概念基本概念图的分类图的表示方法 基本概念 由 顶点(Vertex) 和 边(Edge) 组成的集合。顶点表示图中的点,而边表示顶点之间的连接。记为 G …...
)
技术周总结 09.09~09.15周日(C# WinForm WPF)
文章目录 一、09.09 周一1.1) 问题01: Windows桌面开发中,WPF和WinForm的区别和联系?联系:区别: 二、09.12 周四2.1)问题01:visual studio的相关快捷键有哪些?通用快捷键编辑导航调试窗口管理 2…...
4K投影仪选购全攻略:全玻璃镜头的当贝F6,画面细节纤毫毕现
在当今的投影市场上,4K投影仪已经成了主流产品,越来越多家庭开始关注如何选择一款性价比高、口碑好的4K投影仪。4K投影仪其实指的是具备3840*2160像素分辨率投影仪,它能够提供更清晰、更细腻、更真实的画面效果。 那么4K投影仪该怎么选&…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
