【信息论基础第二讲】离散信源的数学模型及其信息测度包括信源的分类、信源的数学模型、离散信源的信息测度、二元信源的条件熵联合熵
一、信源的分类

二、信源的数学模型
1、信源的概念
在通信系统中,收信者在未收到信息以前,对信源发出什么消息是不确定的、随机的、因此我们可以用随机变量、随机序列或者随机过程来描述信源的输出。严格地说,用概率空间来描述信源输出。
2、信源的分类

(1)离散信源和连续信源
一般不说是离散还是连续我们都默认为离散信源

(2)有记忆信源和无记忆信源
离散无记忆信源:离散信源在不同时刻发出的符号之间是无依赖的彼此统计独立的
(3)平稳信源和不稳定信源
离散平稳信源:离散信源的概率分布不随时间变化
3、信源熵
(1)定义

(2)例子——鉴别伪币问题
24个硬币中有一个伪币,由前一讲已经知道称量三次可以找出伪币,那么每次称量中获得的信息是多少?
抓住信源熵的核心概念“平均不确定度”

三、离散信源的信息测度
信息测度通俗来说就是每输出一个符号携带的信息量。
1、自信息的定义

(1)I(xi) 的含义
当xi输出以前,表示输出xi发生的不确定性
当xi输出以后,表示输出消息xi所包含的信息量
(2)I(xi) 的单位
若取r=2,单位为bit
若取r=e,单位为nat
那么1nat = ?bit

这里需要注意的是虽然单位不同,但是不管是bit还是nat本质上表示的都是I(xi),所以在推导 1nat = ?bit的关系时要带着单位,而且不建议用换底公式因为没有任何的物理意义。
2、联合自信息与条件自信息


四、二元信源的信息熵


五、二元信源的条件熵
1、定义

这里一定要注意是p(xiyi)联合概率加权
2、物理意义
令信源输出为X,信宿接受消息为Y,条件熵H(X/Y)表示信宿在收到Y后,信源X仍然存在的不确定度,这是传输失真造成的,H(X/Y)称为损失熵或者信道疑义度。
条件熵H(Y/X)表示对于信源的输出X,信宿接受Y所存在的不确定度,这是在传输过程中噪声引起的,H(Y/X)称为噪声熵或者信道散布度。
六、二元信源的联合熵

七、熵、条件熵、联合熵之间的关系

H(XY) = H(X) + H(Y/X)
H(XY) = H(Y) + H(X/Y)
H(U1U2U3...UN) = H(U1) + H(U2|U1) + H(U3|U1U2) + ... + H(UN|U1U2U3...UN-1)
相关文章:

【信息论基础第二讲】离散信源的数学模型及其信息测度包括信源的分类、信源的数学模型、离散信源的信息测度、二元信源的条件熵联合熵
一、信源的分类 二、信源的数学模型 1、信源的概念 在通信系统中,收信者在未收到信息以前,对信源发出什么消息是不确定的、随机的、因此我们可以用随机变量、随机序列或者随机过程来描述信源的输出。严格地说,用概率空间来描述信源输出。 …...

在 Spring Boot 项目中连接 IBM AS/400 数据库——详细案例教程
文章目录 1. 添加 jt400 依赖2. 下载 jt400 驱动包依赖下载手动下载下载地址:手动下载 JAR 的步骤: 3. 配置 application.properties 或 application.yml(1)application.properties(2)application.yml 4. 数…...

VUE + NODE 历史版本安装
以node 12.20.0为例子,想下载哪个版本,后面写哪个版本 https://registry.npmmirror.com/binary.html?pathnode/v12.20.0/ 安装国内镜像7.1.0 cnpm npm install -g cnpm7.1.0 -g --registryhttps://registry.npmmirror.com 安装vue脚手架4.5.15 cnpm …...

git reset 几点疑问
疑问:使用 git reset --hard <commit-hash-from-branch-B> 将工作区状态reset为其他branch的某点。 如果当前工作区的分支(比如 branch A)上使用 git reset --hard 将其状态重置为另一个分支(比如 branch B)的某…...
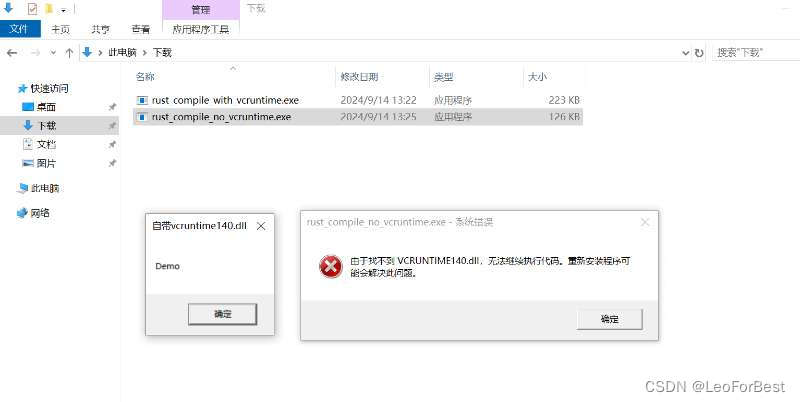
Rust Windows下编译 静态链接VCRuntime140.dll
Rust 编译出来的exe默认动态链接VC运行库,分发电脑上需要安装有Microsoft Visual C Redistributable for Visual Studio 2015运行库。 编译时能静态链接进去,就省去客户端未安装运行库的问题。方法如下: 只需在当前根目录下新建.cargo\config.toml&#…...

从“天宫课堂”到人工智能:中国少儿编程的未来在哪里?
近日,中国载人航天“天宫课堂”第三次开讲,激发了全国数百万青少年对科技的热情。从航天技术到人工智能,科技的快速发展正不断改变我们的生活,也让越来越多的家长意识到,未来属于那些掌握编程和创新思维的孩子。与其让…...

ARM base instruction -- blr
BLR Branch with Link to Register calls a subroutine at an address in a register, setting register X30 to PC4. 带寄存器链接的分支在寄存器中的某个地址调用一个子程序,将寄存器 X30 (lr) 设置为 PC4。 BLR <Xn> BLR 跳转到reg内容地址,…...

宠物猫领养馆会员管理系统---附源码72579
目录 1 绪论 1.1 课题目的与意义 1.2国内外研究现状 1.3论文结构与章节安排 1.4 express框架介绍 2 宠物猫领养馆会员管理系统系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 操作可行性分析 2.2 系统功能分析 2.2.1 功能性分析 2.2.2 …...

驾驶员注意力分神状态检测系统源码分享
驾驶员注意力分神状态检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of …...

基于less和scss 循环生成css
效果 一、less代码 复制代码 item-count: 12; // 生成多少个 .item 类.item-loop(n) when (n > 0) {.icon{n} {background: url(../../assets/images/menu/icon{n}.png) no-repeat;background-size: 100% 100%;}.item-loop(n - 1);}.item-loop(item-count);二、scss代码 f…...

opencv之Canny边缘检测
文章目录 前言1.应用高斯滤波去除图像噪声2.计算梯度3.非极大值抑制4.应用双阈值确定边缘5.Canny函数及使用 前言 Canny边缘检测是一种流行的边缘检测算法,用于检测图像中的边缘。它通过一系列步骤将图像中的像素边缘突出显示出来,主要分为以下几个步骤…...

springBoot 集成https
springBoot 集成https 1、springBoot默认的证书格式 pring Boot 需要 .p12 或 .jks 格式的证书。如果你只有 .pem 和 .key 文件,可以使用 openssl 工具将它们转换成 .p12 文件 2、转换.p12 我的证书文件如下,需要转换 2.1 下载openssl https://slpr…...

数据库连接池与Druid【后端 16】
数据库连接池与Druid 在现代软件开发中,数据库连接池作为一种关键的技术手段,被广泛用于提升数据库访问的效率和稳定性。本文将深入探讨数据库连接池的概念、常见实现,并重点介绍我国阿里集团开源的数据库连接池——Druid,以及如何…...

C#使用Access数据库使用总结
话说这Access数据库确实是有点年代了,前面在深圳的一家放射医疗公司,数据库用的Access,后面在我的建议下,换成了SQLite。用SQLite多舒服,不用装Runtime,还可以用EF。Access得装Runtime,也用不了…...

使用Dataherald组件进行数据分析:从安装到查询的完整指南
使用Dataherald组件进行数据分析:从安装到查询的完整指南 引言 在当今数据驱动的世界中,能够快速、准确地从数据中获取洞察变得越来越重要。Dataherald是一个强大的工具,它可以帮助开发者和数据分析师更轻松地进行数据查询和分析。本文将详…...

sqlx1.3.4版本的问题
sqlx1.3.4版本存在问题,在调用sqlx的Select方法时,如果传入的dest是一个slice且slice不为空,查询结果将会追加在这个slice已有的元素后面。这位用户认为这个行为是“a little surprising”的,且与json 反序列化的表现不一致&#…...

Rust 编译器使用的 C++ 编译器吗?
Rust编译器并不直接使用C编译器,但它们之间可以存在交互,尤其是在Rust与C进行混合编程时。以下是关于Rust编译器和C编译器之间关系的详细解释: 1. Rust编译器的选择 Rust是一种现代化的系统级编程语言,它需要一个可靠的编译器来…...

Python计算机视觉 第10章-OpenCV
Python计算机视觉 第10章-OpenCV OpenCV 是一个C 库,用于(实时)处理计算视觉问题。实时处理计算机视觉的 C 库,最初由英特尔公司开发,现由 Willow Garage 维护。OpenCV 是在 BSD 许可下发布的开源库,这意味…...
)
多层感知机 (Multilayer Perceptron, MLP)
多层感知机 (Multilayer Perceptron, MLP) 通俗易懂算法 多层感知机(Multilayer Perceptron,MLP)是一种前馈人工神经网络。它的主要特点是由多层神经元(或节点)组成,包括至少一个隐藏层。MLP 是监督学习的…...

reg和wire的区别 HDL语言
文章目录 数据类型根本区别什么时候要定义wire小结 数据类型 HDL语言有三种数据类型:寄存器数据类型(reg)、线网数据类型(wire)、参数数据类型(parameter)。 根本区别 reg: 寄存器…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
