初阶数据结构【TOP】- 11.普通二叉树的介绍 - 1. (细致,保姆~~!)
文章目录
- 前言
- 一、普通二叉树的链式结构
- 二、 造树
- 三、普通二叉树的遍历
- 四、遍历完整代码
- 五、总结
前言
本篇文章笔者将会对普通二叉树部分进行细致的讲解 , 本篇主要包括以下内容: 二叉树链式结构的介绍 ,二叉树的遍历. 笔者会一步一步分析带学者领略递归的美好~~
一、普通二叉树的链式结构
在前面章节中 , 笔者对特殊二叉树部分进行了讲解, 特殊二叉树是基于数组实现的 ,但对于普通二叉树来说就要使用链式结构来实现了 ,以下将具体介绍 !
那么什么是链式结构呢 ? 这里就好比如链表 , 是一个一个节点组成. 这里笔者推荐一种特殊方法 : 左孩子 , 右兄弟表示法 .
● 左孩子右兄弟表示法
顾名思义: 我们要定义两个指针 , 一个指向左孩子 , 一个指向右孩子(左孩子的右兄弟).

● 链式结构表示法
// 普通二叉树typedef int OrdBinTreeDataType;// 普通二叉树的链式声明
typedef struct OrdBinTree
{OrdBinTreeDataType data;struct OrdBinTree* Left;struct OrdBinTree* Right;
}OBTree;二、 造树
在当前阶段 , 笔者建议学者采用 " 手动造树 " 的方法 , 这种方法同样也是我们在遇到一些相关OJ问题时可以采用的一种寻找问题的方法 .
● 手动造树
typedef int OrdBinTreeDataType;// 普通二叉树的链式声明
typedef struct OrdBinTree
{OrdBinTreeDataType data;struct OrdBinTree* Left;struct OrdBinTree* Right;
}OBTree;//手动造树
OBTree* ByNode(int x)
{OBTree* node = (OBTree*)malloc(sizeof(OBTree));if (node == NULL){perror("malloc fail! ");return NULL;}node->data = x;node->Left = node->Right = NULL;return node;
}OBTree* CreatTree()
{OBTree* node1 = ByNode(1);OBTree* node2 = ByNode(2);OBTree* node3 = ByNode(3);OBTree* node4 = ByNode(4);OBTree* node5 = ByNode(5);OBTree* node6 = ByNode(6);//连接node1->Left = node2;node1->Right = node4;node2->Left = node3;node4->Left = node5;node4->Right = node6;return node1;}当树造好了以后就可以开始学习 , 树的遍历相关知识了 .
三、普通二叉树的遍历
● 分类
这里讨论 : 前序遍历 , 中序遍历 , 后序遍历 , 层序遍历 .
这里笔者介绍前三种~
首先 , 这里的 前 , 中 , 后 , 指的是根的位置是 : 前 , 中 , 后.
在实现这些变量之前 , 笔者介绍一种方法 , 分支递归
● 实现思想
首选 , 对于二叉树我们知道二叉树是由递归定义的 , 所以在普通二叉树中可以采用递归的思想来进行, 递归 : 大问题化小问题 ,直至问题解决 .
其次, 任何一颗树都是由根节点和子树构成 , 这是分支递归的核心 !

这里 , 理解递归的概念 : 递则往下一层一层递 , 归则往回一层一层归. 也就是说 : 每次的归只能归回该函数的上一层. (这是极其重要的 !)
★ 递归解释图:

那么什么是分支递归, 其实就是逐渐拆解成小问题得递归 , 以下将会有所体会 ~~
● 实现
◐ 前序遍历
形式: 根 , 左节点 , 右节点 . (遍历顺序) . 遇到空树才停止 " 递 ".
这里笔者先给出前序遍历代码 ,以便学者理解 !
★ 代码
//前序遍历
void PreOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}printf("%d ", tree->data); // 根PreOrder(tree->Left); //左孩子PreOrder(tree->Right); //右孩子}
访问顺序 :
★ 递

- 访问到根 - 1 的位置
- 访问绿色左树 , 但绿色左树不为空 , 则继续向下访问 .
- 访问绿色部分的根 - 2 的位置
- 访问红色部分 , 但红色左树不为空 , 则继续向下访问 .
- 访问红色部分的根 - 3 的位置
- 访问蓝色部分 , 蓝色部分为空 , 则停止 ’ 递 ’ .
! 蓝色数字部分为优先访问的节点值 !
♦ 递过程的打印
因为此为前序遍历 , 故每一次递是先访问根的 , 根据以上代码 , 则 : 会优先打印出
1 2 3

那么右边分析同上即可.
★ 归

★ 详细流程

每一个节点的递归与其一样 , 同样分析即可 !
★ 递归展开图


执行完以上过程 , 则最终打印结果为 :


◐ 中序遍历
经过以上细致的分析 ,相信学者对遍历有所认识 , 那么中序 , 后序就显得特别简单了, 无非就是根的位置不同的区别
★ 代码
//中序遍历
void InOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}InOrder(tree->Left);printf("%d ", tree->data); InOrder(tree->Right);
}★ 结果

◐ 后序遍历
//后序遍历
void AfterOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}AfterOrder(tree->Left);AfterOrder(tree->Right);printf("%d ", tree->data);}
★ 结果

四、遍历完整代码
#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>
//树的遍历
typedef int OrdBinTreeDataType;// 普通二叉树的链式声明
typedef struct OrdBinTree
{OrdBinTreeDataType data;struct OrdBinTree* Left;struct OrdBinTree* Right;
}OBTree;//手动造树
OBTree* ByNode(int x)
{OBTree* node = (OBTree*)malloc(sizeof(OBTree));if (node == NULL){perror("malloc fail! ");return NULL;}node->data = x;node->Left = node->Right = NULL;return node;
}OBTree* CreatTree()
{OBTree* node1 = ByNode(1);OBTree* node2 = ByNode(2);OBTree* node3 = ByNode(3);OBTree* node4 = ByNode(4);OBTree* node5 = ByNode(5);OBTree* node6 = ByNode(6);//连接node1->Left = node2;node1->Right = node4;node2->Left = node3;node4->Left = node5;node4->Right = node6;return node1;}//前序遍历
void PreOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}printf("%d ", tree->data); // 根PreOrder(tree->Left); //左孩子PreOrder(tree->Right); //右孩子}//中序遍历
void InOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}InOrder(tree->Left);printf("%d ", tree->data); InOrder(tree->Right);
}//后序遍历
void AfterOrder(OBTree* tree)
{if (tree == NULL){printf("NULL ");return;}AfterOrder(tree->Left);AfterOrder(tree->Right);printf("%d ", tree->data);}
int main()
{OBTree* tree = CreatTree();printf("前序: \n");PreOrder(tree);printf("\n");printf("中序: \n");InOrder(tree);printf("\n");printf("后序: \n");AfterOrder(tree);printf("\n");return 0;}

五、总结
以上是对二叉树的遍历的讲解 ,其实就是对递归的深入 ,相信大家通过学习会有所收获 !
相关文章:

初阶数据结构【TOP】- 11.普通二叉树的介绍 - 1. (细致,保姆~~!)
文章目录 前言一、普通二叉树的链式结构二、 造树三、普通二叉树的遍历四、遍历完整代码五、总结 前言 本篇文章笔者将会对普通二叉树部分进行细致的讲解 , 本篇主要包括以下内容: 二叉树链式结构的介绍 ,二叉树的遍历. 笔者会一步一步分析带学者领略递归的美好~~ 一、普通二叉…...

【pyenv】pyenv安装版本超时的解决方案
目录 1、现象 2、分析现象 3、手动下载所需版本 4、存放到指定路径 5、重新安装 6、pip失败(做个记录,未找到原因) 7、方法二修改环境变量方法 7.1 设置环境变量 7.2 更新 7.3 安装即可 8、方法三修改XML文件 前言:研…...

【新片场-注册安全分析报告-无验证方式导致安全隐患】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 1. 暴力破解密码,造成用户信息泄露 2. 短信盗刷的安全问题,影响业务及导致用户投诉 3. 带来经济损失,尤其是后付费客户,风险巨大,造…...

新160个crackme - 057-bbbs-crackme04
运行分析 因软件版本老旧,需使用windows XP虚拟机运行有个SystemID,值为12345678需破解User ID和Password PE分析 yC壳,32位 OD手动脱壳 使用windows XP虚拟机,将程序拖入OD按一下F8,ESP变红,根据ESP定律设…...

车机中 Android Audio 音频常见问题分析方法实践小结
文章目录 前言1. 无声2. 断音3. 杂音4. 延迟播放5. 焦点问题6. 无声问题(连上 BT )其他完善中…… 前言 本文主要总结了一下车机开发中遇到的 Audio 有关的问题,同时参考网上的一案例,由于Audio 模块出现音频问题的场景很多,对每一个出现的问…...

湘大 OJ 代码仓库
有时候不需要上传一些题解,想要上传一些纯代码就行,傻傻把代码上传到文章里面,感觉效率不是很高,还是建立一个代码仓库比较方便 需要会使用魔法可能才能访问,github代码仓库地址...
Ruoyi Cloud K8s 部署
本文视频版本:https://www.bilibili.com/video/BV1xF4Se3Esv 参考 https://blog.csdn.net/Equent/article/details/137779505 https://blog.csdn.net/weixin_48711696/article/details/138117392 https://zhuanlan.zhihu.com/p/470647732 https://gitee.com/y_project/Ruo…...

OpenGL Texture C++ Camera Filter滤镜
基于OpenGL Texture纹理的强大功能,在片段着色器(Shader)中编写GLSL代码,对YUV的数据进行数据转换从而实现视频编辑软件中的相机滤镜功能。 接上一篇OpenGL Texture C 预览Camera视频的功能实现,本篇来实现Camera滤镜效…...

基于Sobel算法的边缘检测设计与实现
1、边缘检测 针对的时灰度图像,顾名思义,检测图像的边缘,是针对图像像素点的一种计算,目的时标识数字图像中灰度变化明显的点,图像的边缘检测,在保留了图像的重要结构信息的同时,剔除了可以认为…...

java:练习
编写一个 Java 程序,计算并输出从 1 到用户指定的数字 n 中,所有“幸运数字”。幸运数字的定义如下:条件 1:数字的所有位数(如个位、十位)加起来的和是 7 的倍数。条件 2:数字本身是一个质数&am…...

大数据中一些常用的集群启停命令
文章目录 一、HDFS二、MapReduce && YARN三、Hive 一、HDFS 格式化namenode # 确保以hadoop用户执行 su - hadoop # 格式化namenode hadoop namenode -format启动 # 一键启动hdfs集群 start-dfs.sh # 一键关闭hdfs集群 stop-dfs.sh# 如果遇到命令未找到的错误&#…...

Golang、Python、C语言、Java的圆桌会议
一天,Golang、C语言、Java 和 Python 四位老朋友坐在编程领域的“圆桌会议”上,讨论如何一起完成一个任务:实现一个简单的高并发服务器,用于处理成千上万的请求。大家各抒己见,而 Golang 则是这次会议的主角。 1. Pyth…...

C语言编译原理
目录 一、C语言的编译过程 二、预处理 三、编译阶段 3.1 词法分析(Lexical Analysis) 3.2 语法分析(Syntax Analysis) 语法分析的主要步骤: 语法分析的关键技术: 构建AST: 符号表的维护…...

【c++】类和对象(下)(取地址运算符重载、深究构造函数、类型转换、static修饰成员、友元、内部类、匿名对象)
🌟🌟作者主页:ephemerals__ 🌟🌟所属专栏:C 目录 前言 一、取地址运算符重载 1. const修饰成员函数 2. 取地址运算符重载 二、深究构造函数 三、类型转换 四、static修饰成员 1. static修饰成员变…...

Apache POI 学习
Apache POI 学习 1. 引言2. 环境搭建MavenGradle 3. 基础概念4. 基本操作4.1 创建 Excel 文件4.2 读取 Excel 文件 5. 进阶操作5.1 设置单元格样式5.2 数据验证5.3 图表创建5.4 合并单元格5.5 居中对齐5.6 设置边框和字体颜色 6. 性能优化7. 总结 1. 引言 Apache POI 是一个用…...

福建科立讯通信 指挥调度管理平台 SQL注入漏洞
北峰通信-福建科立讯通信 指挥调度管理平台 SQL注入漏洞 厂商域名和信息收集 域名: 工具sqlmap python sqlmap.py -u "http://ip:端口/api/client/down_file.php?uuid1" --batch 数据包 GET /api/client/down_file.php?uuid1%27%20AND%20(SELECT%20…...

4.qml单例模式
这里写目录标题 js文件单例模式qml文件单例模式 js文件单例模式 直接添加一个js文件到qml中 修改内容 TestA.qml import QtQuick 2.0 import QtQuick.Controls 2.12 import "./MyWork.js" as MWItem {Row{TextField {onEditingFinished: {MW.setA(text)}}Button…...

CACTI 0.8.7 迁移并升级到 1.2.7记录
升级前后环境 升级前: CactiEZ 中文版 V10 升级后: Ubuntu 2204 Cacti 1.2.7 升级原因:风险漏洞太多,升不尽,补不完. 升级流程 Created with Raphal 2.3.0 开始 DST:安装Ububtu/Mariadb/apache/php SRC:备份 DB/RRA 数据导入 结束 Cacti 依赖包 注意:UBUNTU下有些包,它非另外…...
OrionX vGPU 研发测试场景下最佳实践之Jupyter模式
在上周的文章中,我们讲述了OrionX vGPU研发测试场景下最佳实践之SSH模式,今天,让我们走进 Jupyter模式下的最佳实践。 • Jupyter模式:Jupyter是最近几年算法人员使用比较多的一种工具,很多企业已经将其改造集成开发工…...

国风编曲:了解国风 民族调式 五声音阶 作/编曲思路 变化音 六声、七声调式
中国风 以流行为基础加入中国特色乐器、调式、和声融为一体的风格 如:青花瓷、菊花台、绝代风华、江南等等等等 省流:中国风=流行民族乐 两者结合,民族元素越多越中国风 流行民族/摇滚民族/电子民族 注意:中国风≠…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
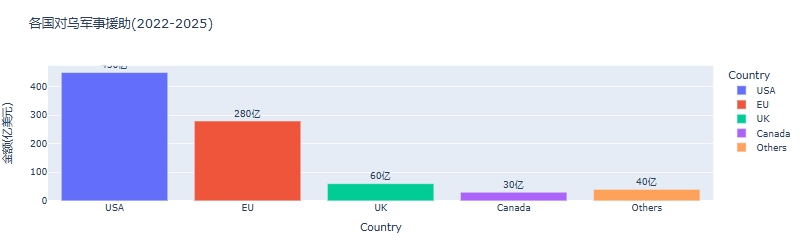
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
