【ShuQiHere】 进制转换的世界:从十进制到二进制、十六进制的转换技巧
【ShuQiHere】
在计算机科学中,进制转换(Radix Conversion) 是一个基础且非常重要的技能。无论是理解计算机的存储、数据表示,还是在编程中处理不同的进制数据,进制转换都是不可或缺的。本文将详细讲解 十进制(Decimal, 10进制)、二进制(Binary, 2进制) 和 十六进制(Hexadecimal, 16进制) 之间的转换,帮助你扎实掌握这些技巧,并通过丰富的例子加深理解。🧠
什么是进制?🧮
进制是表示数字的方式。每种进制都有其基数(Base),表示该进制每一位数字可以取的值的范围。常见的进制有:
- 十进制(Decimal, base-10):我们日常使用的数字系统,基数为10,使用的符号是0-9。
- 二进制(Binary, base-2):计算机底层使用的数字系统,基数为2,符号是0和1。🖥️
- 十六进制(Hexadecimal, base-16):常用于计算机系统,基数为16,符号是0-9和A-F,其中A表示10,B表示11,依此类推,直到F表示15。💡
进制的实际应用
- 二进制(Binary, 2进制) 是计算机中最底层的数据表示方式,计算机存储和处理的数据都是以二进制形式存储的。
- 十六进制(Hexadecimal, 16进制) 通常用于简化二进制表示。一个十六进制数字可以表示四位二进制数字(4 bits),因此它在表示内存地址和机器码时非常方便。
现在让我们通过更详细的例子来深入理解不同进制之间的转换!🚀
1. 十进制转二进制(Decimal to Binary, 10-2) ⚙️
十进制转二进制通常使用 除2取余法。这个方法的核心是不断将十进制数除以2,记录每次除法的余数,直到商为0。最后,将余数逆序排列得到二进制数。
步骤:
- 将十进制数不断除以 2,并记录每次的余数。
- 将余数从最后一次除法结果开始反向排列,得到最终的二进制结果。
示例:
将 59 转换为二进制:
- 59 ÷ 2 = 29,余数 1
- 29 ÷ 2 = 14,余数 1
- 14 ÷ 2 = 7,余数 0
- 7 ÷ 2 = 3,余数 1
- 3 ÷ 2 = 1,余数 1
- 1 ÷ 2 = 0,余数 1
将余数逆序排列得到:
59_{10} = 111011_2
背景知识:
在计算机存储中,二进制 是最基础的表示方式。每个二进制位(bit)表示一个最小存储单元,且每一位只有两种可能的状态:0 或 1。
Java代码手动实现:
public class DecimalToBinaryManual {public static String decimalToBinary(int n) {StringBuilder binaryNum = new StringBuilder();while (n > 0) {binaryNum.append(n % 2);n = n / 2;}return binaryNum.reverse().toString();}public static void main(String[] args) {System.out.println(decimalToBinary(59)); // 输出: 111011}
}
2. 十进制转十六进制(Decimal to Hexadecimal, 10-16) 🔢
将十进制数转换为十六进制可以使用 除16取余法。通过不断将十进制数除以16并记录余数,最后将余数逆序排列即可得到十六进制数。
步骤:
- 将十进制数不断除以 16,并记录每次的余数。
- 余数部分对应十六进制的符号:0-9 对应本身,10-15 对应 A-F。
- 将余数逆序排列,得到最终的十六进制数。
示例:
将 1234 转换为十六进制:
- 1234 ÷ 16 = 77,余数 2
- 77 ÷ 16 = 4,余数 13 (对应十六进制的 D)
- 4 ÷ 16 = 0,余数 4
将余数逆序排列,得到:
1234_{10} = 4D2_{16}
背景知识:
十六进制 通常用来简化二进制表示,因为一个十六进制数字正好可以表示四个二进制位。计算机中很多底层信息,如内存地址、颜色代码等,都是通过十六进制来表示的。
Java代码手动实现:
public class DecimalToHexadecimalManual {public static String decimalToHexadecimal(int n) {StringBuilder hexNum = new StringBuilder();char[] hexDigits = "0123456789ABCDEF".toCharArray();while (n > 0) {hexNum.append(hexDigits[n % 16]);n = n / 16;}return hexNum.reverse().toString();}public static void main(String[] args) {System.out.println(decimalToHexadecimal(1234)); // 输出: 4D2}
}
3. 十六进制转十进制(Hexadecimal to Decimal, 16-10) 🖥️
要将 十六进制 转换为 十进制,我们使用 权值展开法。将每一位十六进制数乘以16的相应幂次,再将结果相加得到十进制数。
步骤:
- 从右向左,每一位乘以 (16) 的相应幂次。
- 将结果相加,得到十进制数。
示例:
将 1A3F_{16} 转换为十进制:
[
1 A 3 F 16 = ( 1 × 1 6 3 ) + ( 10 × 1 6 2 ) + ( 3 × 1 6 1 ) + ( 15 × 1 6 0 ) = 4096 + 2560 + 48 + 15 = 671 9 10 1A3F_{16} = (1 \times 16^3) + (10 \times 16^2) + (3 \times 16^1) + (15 \times 16^0) = 4096 + 2560 + 48 + 15 = 6719_{10} 1A3F16=(1×163)+(10×162)+(3×161)+(15×160)=4096+2560+48+15=671910
]
背景知识:
十六进制的每一位代表的权重是 (16^n),这使得它非常适合表示较大的数,同时可以减少书写的长度。内存地址、汇编语言中的指令都是用十六进制表示的。
Java代码手动实现:
public class HexadecimalToDecimalManual {public static int hexadecimalToDecimal(String hexNum) {int decimal = 0;int base = 1; // 16^0char[] hexDigits = hexNum.toUpperCase().toCharArray();int len = hexDigits.length;for (int i = len - 1; i >= 0; i--) {if (hexDigits[i] >= '0' && hexDigits[i] <= '9') {decimal += (hexDigits[i] - '0') * base;} else if (hexDigits[i] >= 'A' && hexDigits[i] <= 'F') {decimal += (hexDigits[i] - 'A' + 10) * base;}base *= 16;}return decimal;}public static void main(String[] args) {System.out.println(hexadecimalToDecimal("1A3F")); // 输出: 6719}
}
4. 十六进制转二进制(Hexadecimal to Binary, 16-2) 🧑💻
十六进制转二进制 非常简单。每一个十六进制数字对应四位二进制数。只需将每位十六进制数字分别转换成四位二进制数,最后将它们拼接起来。
步骤:
- 将每一个十六进制位转换为对应的四位二进制数。
- 将这些二进制数拼接在一起
,得到最终的二进制结果。
示例:
将 1A3F_{16} 转换为二进制:
- 1 = 0001
- A = 1010
- 3 = 0011
- F = 1111
所以:
1A3F_{16} = 0001\ 1010\ 0011\ 1111_2
背景知识:
二进制与十六进制之间的转换非常简便,尤其在处理大型的二进制数据时,十六进制能帮助我们更轻松地表示和阅读数据。许多程序员在调试时经常用到十六进制,因为它可以让复杂的二进制变得更加清晰易读。
Java代码手动实现:
public class HexadecimalToBinaryManual {public static String hexadecimalToBinary(String hexNum) {StringBuilder binary = new StringBuilder();char[] hexDigits = hexNum.toUpperCase().toCharArray();for (char hexDigit : hexDigits) {switch (hexDigit) {case '0': binary.append("0000"); break;case '1': binary.append("0001"); break;case '2': binary.append("0010"); break;case '3': binary.append("0011"); break;case '4': binary.append("0100"); break;case '5': binary.append("0101"); break;case '6': binary.append("0110"); break;case '7': binary.append("0111"); break;case '8': binary.append("1000"); break;case '9': binary.append("1001"); break;case 'A': binary.append("1010"); break;case 'B': binary.append("1011"); break;case 'C': binary.append("1100"); break;case 'D': binary.append("1101"); break;case 'E': binary.append("1110"); break;case 'F': binary.append("1111"); break;}}return binary.toString();}public static void main(String[] args) {System.out.println(hexadecimalToBinary("1A3F")); // 输出: 0001101000111111}
}
5. 二进制转十进制(Binary to Decimal, 2-10) 💡
将 二进制 转换为 十进制 可以使用 权值展开法。二进制的每一位表示 2 的幂次方,通过计算每一位二进制对应的十进制值,并将这些值相加得到最终的十进制结果。
步骤:
- 将每个二进制位乘以 2 的幂次方。
- 将结果相加,得到十进制数。
示例:
将 1101101_2 转换为十进制:
[
110110 1 2 = ( 1 × 2 6 ) + ( 1 × 2 5 ) + ( 0 × 2 4 ) + ( 1 × 2 3 ) + ( 1 × 2 2 ) + ( 0 × 2 1 ) + ( 1 × 2 0 ) = 64 + 32 + 0 + 8 + 4 + 0 + 1 = 10 9 10 1101101_2 = (1 \times 2^6) + (1 \times 2^5) + (0 \times 2^4) + (1 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) = 64 + 32 + 0 + 8 + 4 + 0 + 1 = 109_{10} 11011012=(1×26)+(1×25)+(0×24)+(1×23)+(1×22)+(0×21)+(1×20)=64+32+0+8+4+0+1=10910
]
背景知识:
二进制 是计算机唯一能直接理解的数字系统。每一个二进制位(bit)都代表一个最小的存储单元,而它的值只能是 0 或 1。
Java代码手动实现:
public class BinaryToDecimalManual {public static int binaryToDecimal(String binaryNum) {int decimal = 0;int base = 1; // 2^0int len = binaryNum.length();for (int i = len - 1; i >= 0; i--) {if (binaryNum.charAt(i) == '1') {decimal += base;}base *= 2;}return decimal;}public static void main(String[] args) {System.out.println(binaryToDecimal("1101101")); // 输出: 109}
}
6. 二进制转十六进制(Binary to Hexadecimal, 2-16) 🔄
二进制转十六进制 的转换方法非常简单,只需将二进制数每四位一组,转换为对应的十六进制数即可。
步骤:
- 将二进制数从右往左按四位分组。
- 将每组二进制数转换为对应的十六进制数。
示例:
将 1101101011_2 转换为十六进制:
- 从右向左分组:
1101和1011 - 转换:
- 1101 = D
- 1011 = B
所以:
1101101011_2 = 1DB_{16}
背景知识:
二进制 与 十六进制 之间的转换在计算机系统中非常常见。二进制数非常冗长且不易阅读,而十六进制数能简化表示,同时能保留二进制信息的精确度。
Java代码手动实现:
public class BinaryToHexadecimalManual {public static String binaryToHexadecimal(String binaryNum) {StringBuilder hex = new StringBuilder();int len = binaryNum.length();// 补齐长度为4的倍数while (len % 4 != 0) {binaryNum = "0" + binaryNum;len++;}for (int i = 0; i < len; i += 4) {String fourBits = binaryNum.substring(i, i + 4);switch (fourBits) {case "0000": hex.append("0"); break;case "0001": hex.append("1"); break;case "0010": hex.append("2"); break;case "0011": hex.append("3"); break;case "0100": hex.append("4"); break;case "0101": hex.append("5"); break;case "0110": hex.append("6"); break;case "0111": hex.append("7"); break;case "1000": hex.append("8"); break;case "1001": hex.append("9"); break;case "1010": hex.append("A"); break;case "1011": hex.append("B"); break;case "1100": hex.append("C"); break;case "1101": hex.append("D"); break;case "1110": hex.append("E"); break;case "1111": hex.append("F"); break;}}return hex.toString();}public static void main(String[] args) {System.out.println(binaryToHexadecimal("1101101011")); // 输出: 1DB}
}
总结 🎯
在这篇博客中,我们通过丰富的例子讲解了六种常见的进制转换方式:从 十进制到二进制、十进制到十六进制,再到 二进制、十六进制与十进制之间的转换。掌握这些进制转换技巧不仅有助于理解计算机底层数据的表示,还能帮助你在编程和调试中更加得心应手。
- 十进制转二进制(10-2):除2取余法
- 十进制转十六进制(10-16):除16取余法
- 十六进制转十进制(16-10):权值展开法
- 十六进制转二进制(16-2):每位对应四位二进制
- 二进制转十进制(2-10):权值展开法
- 二进制转十六进制(2-16):每四位二进制对应一位十六进制
进制转换是每个计算机组成原理课程的基础内容,它不仅帮助我们理解计算机如何存储和处理数据,还在编程和系统开发中有着广泛的应用。希望本文能够帮助你深入理解这些关键概念,成为进制转换的高手!💻✨
相关文章:

【ShuQiHere】 进制转换的世界:从十进制到二进制、十六进制的转换技巧
【ShuQiHere】 在计算机科学中,进制转换(Radix Conversion) 是一个基础且非常重要的技能。无论是理解计算机的存储、数据表示,还是在编程中处理不同的进制数据,进制转换都是不可或缺的。本文将详细讲解 十进制&#x…...

《化工管理》
《化工管理》征稿简则 《化工管理》杂志是由中国石油和化学工业联合会主管、中国化工企业管理协会主办,1986年创刊,在国内外公开发行,国内统一连续出版物号:CN 11—3991/F,中国标准连续出版物号:ISSN 1008—…...

LeetCode70:爬楼梯
class Solution { public:int climbStairs(int n) {if(n 1) return 1;if(n 2) return 2;vector<int> dp(n 1, 0);dp[1] 1;dp[2] 2;for(int i 3; i < n 1; i){dp[i] dp[i - 1] dp[i - 2];}return dp[n];} }; 这个题目也就是最简单的动态规划,题目…...

[程序员] 前人留下的苦难源,我们是否有勇气改正?
最近遇到一个客户现场发现的,表象是网络有问题,分析一圈下来发现是程序进入了某种死循环状态,耗尽CPU。 产品里的很多线程/进程的优先级设置的很高,甚至高过了内核运行程序的优先级,高过了产品内警告处理程序的运行&a…...
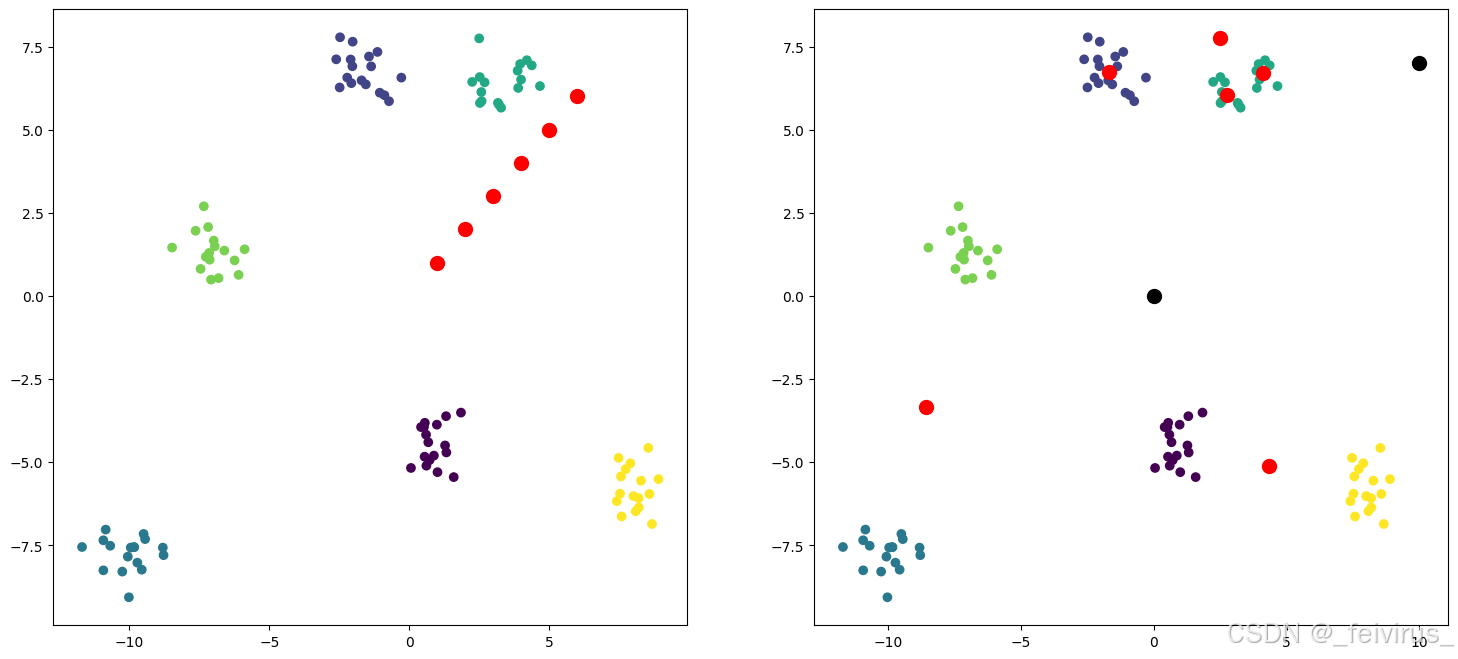
聚类_K均值
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs1.数据预处理 #创建基于高斯分布的样本点, x是点的坐标,y是所属聚类值 x, y make_blobs(n_samples100, centers6, random_state100, cluster_std0.6) # 设置图形尺寸…...

Mac电脑剪切板在哪里找 苹果电脑剪切板打开教程【详解】
Windows 和 Mac 电脑在使用方式上存在一些差异,许多习惯了 Windows 系统的用户初次接触 Mac 时可能会对某些操作感到困惑。比如,很多人会问:Mac 上的剪贴板在哪里?如果你也有这样的疑问,不妨看看下面这篇关于如何在 Ma…...

Python编程 - 三器一包
目录 前言 一、迭代器 (一)基本概念 (二)迭代器和可迭代对象 (三)创建迭代器 (四)内置迭代器函数 (五)优点和局限性 二、生成器 (一&…...

InternVL 多模态模型部署微调实践
友情链接 该文档参考InternVL垂直领域场景微调实践而写成,感谢社区同学法律人的文档。 写在前面(什么是InternVL) InternVL 是一种用于多模态任务的深度学习模型,旨在处理和理解多种类型的数据输入,如图像和文本。它…...

Ruby Dir 类和方法
Ruby Dir 类和方法 Ruby 中的 Dir 类提供了用于处理目录的各种方法。这些方法允许您列出目录内容、更改当前工作目录、创建和删除目录等。本文将详细介绍 Dir 类的常用方法,并通过示例展示如何使用它们。 目录 Dir 类的简介常用方法 Dir.chdirDir.childrenDir.de…...

C++STL~~deque
文章目录 deque的概念deque的使用deque的练习总结 deque的概念 deque(双端队列):是一种序列容器、是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1)ÿ…...

SpringCloud的学习,Consul服务注册与发现、分布式配置,以及 服务调用和负载均衡
介绍 Consul 是一套开源的分布式服务发现和配置管理系统,由 HashiCorp 公司用 Go 语言开发。 提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个都可以根据需要单独使用,也可以一起使用以构建全方位的服务网格,…...

闯关leetcode——26. Remove Duplicates from Sorted Array
大纲 题目地址内容 解题代码地址 题目 地址 https://leetcode.com/problems/remove-duplicates-from-sorted-array/description/ 内容 Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appear…...

基于A2C与超启发式的航天器星载自主任务规划算法-笔记
1. Actor-Critic 模块 主要文件:AC.py, PolicyNet.py, ValueNet.py作用:该模块实现了 A2C(Advantage Actor-Critic)强化学习算法。其中,ActorCritic 类是核心,它同时管理策略网络(Actor&#x…...

[机器学习]决策树
1 决策树简介 2 信息熵 3 ID3决策树 3.1 决策树构建流程 3.2 决策树案例 4 C4.5决策树 5 CART决策树(分类&回归) 6 泰坦尼克号生存预测案例 import pandas as pd from sklearn.model_selection import train_test_split from sklearn.tree import …...

CentOS7更换阿里云yum更新源
目前CentOS内置的更新安装源经常报错无法更新,或者速度不够理想,这个时候更换国内的镜像源就是一个不错的选择。 备份内置更新源 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup 下载阿里云repo源(需要系统…...

算法参数对拥塞控制的影响
来看看参数对公平收敛的影响。仅假象一下就知道应该是个加权公平,但事实如何,还是要具体看一下。 首先看 aimd,标准的 reno 算法是每 round 之后 cwnd 加 1,但如果有些流加 1,有些流加 2,会如何࿱…...

Go websocket
Go 中的 gorilla/websocket 是一个常用且高效的 WebSocket 实现库,可以帮助你轻松地在 Web 应用中实现实时通信。学习 gorilla/websocket 的基本用法包括建立 WebSocket 连接、发送和接收消息、处理错误、以及在实际场景中的使用。以下是关于 gorilla/websocket 的学…...

C# 委托与事件 观察者模式
委托与事件是一种观察者模式。 什么是委托与事件 在c#中,委托类似于代理,也跟其它语言的函数指针、回调函数等相似,但委托是类型安全和可靠的。声明自定义委托时,加上delegate关键字,委托定义类似于接口。 事件是特殊…...

K8S - 用service account 登陆kubectl
刚安装好k8s时 我就可以用kubectl 在master server里管理k8s的资源。 这时我们是感觉不到 k8s的用户和权限管理存在的, 但是其实用户的配置都在kubeclt 的配置文件中 /etc/kubernetes/admin.conf 中 我们可以用下命令来查看当前正在用的帐号 rootk8s-master:~/.d…...

Redis 持久化机制详解
引言 Redis 是一款基于内存的高性能键值存储系统,为了在数据丢失时能快速恢复,Redis 提供了多种持久化机制。这些持久化机制可以将内存中的数据存储到磁盘上,确保即使系统重启或宕机后也能恢复数据。Redis 支持两种主要的持久化方式…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
