「数组」堆排序 / 大根堆优化(C++)
目录
概述
核心概念:堆
堆结构
数组存堆
思路
算法过程
up()
down()
Code
优化方案
大根堆优化
Code(pro)
复杂度
总结
概述
在「数组」快速排序 / 随机值优化|小区间插入优化(C++)中,我们介绍了三种基本排序中的冒泡排序与分治思想结合的算法:快速排序。
本文我们来讲第二种基本排序:选择排序与分治思想结合的产物:堆排序。
我们来回想选择排序:每次选出最小的元素放在数组头部位置,每次都扫描一遍整个数组,整体表现为O(n²)。
我们希望只进行少量比较就能得出数组中的最小元素,该怎么做呢?堆这种结构给了我们一点启发。
核心概念:堆
堆是一颗完全二叉树,它的特点是可以用一维数组来储存。
堆结构
在初学数组排序阶段就理解二叉树似乎有些困难,不过好在我们不必完全了解二叉树的所有概念。
我们只需要知道:
①一个堆是一个层状结构,除去最底一层,每层的每个节点都有左子节点和右子节点,层层布满。
节点从上到下,从左到右依次编号。
(对于这样的结构,我们称之为二叉树,每个父节点都有左右孩子指针指向子节点。)

②只有最后一层允许节点不排满,但节点的排布仍然是严格从左到右的。
如下,图一和图二都是堆,但图三不是堆,因为它的最底层排布不是从左到右的。



③堆有两种:小根堆和大根堆。
小根堆要求父节点的值小于它的两个孩子,大根堆要求父节点的值大于它的两个孩子。
我们称二叉树的头结点为根,所以这种命名就很好理解了:小根堆的根最小,大根堆的根最大。
数组存堆
此时此刻我们完全不必知道二叉树的标准结构,因为数组就可以储存堆。
观察:

我们发现,一个序号从0开始的堆结构,
对于第idx个节点:
父节点序号:(idx-1)/2。
左子节点序号:idx*2+1。
右子节点序号:idx*2+2。
也就是说,对于上图这样的堆,我们将它存入数组应该是这样的:
i 0 1 2 3 4 5 6
int arr[i] 10 15 30 40 50 100 40因此,对于一个堆,我们可以用数组来表示它。
思路
堆这种结构只是为我们的选择排序优化服务的。
选择排序需要我们每次找到最小的元素,那么我们不妨对数组建堆(又称堆化),获得一个小根堆数组后,堆顶,也就是序号为0的数组位置,自然就是我们要的最小元素。
获得最小元素后堆顶出堆,对剩余元素重新堆化,堆顶每次都是剩余元素中的最小元素。
我们不断进行堆顶出堆,就实现了选择排序。
考虑到堆化是按层实现的,因此若有n个元素,则有logn层,重新堆化的过程中内部重排最多进行logn次,通过logn次比较获得最小元素,这显然优于暴力选择排序。
算法过程
堆排序由两个操作构成:上浮up和下沉down。
我们先用宏定义描述一下节点父子关系,另有swap函数实现功能封装:
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void swap(int& a, int& b) {int temp = b;b = a, a = temp;
}up()
对数组进行初始堆化时,依靠上浮实现。
将堆的大小称为size,数组的整体长度称为len。
我们将数组arr分割成两部分:已经堆化的[0,size),未堆化的剩余部分[size,len)
我们将剩余部分的第一个数加入堆中,它显然处于堆底,为了让它处于小根堆中合适的位置,我们进行对它上浮操作。
int size = 0;
for (int i = 0; i < len; i++) {up(arr, i);size++;
}当idx为0时,不再上浮,否则判断此节点与其父亲的大小关系。
我们维护小根堆,所以如果父节点较大,则两者进行交换,使得父节点较小。
然后跟踪父节点,对父节点继续执行上浮操作。(这里的递归操作顺理成章的出现了)
void up(int arr[], int idx) {if (idx && arr[father(idx)] > arr[idx]) {swap(arr[father(idx)], arr[idx]);up(arr, father(idx));}
}down()
数组完全堆化后,我们开始进行堆顶出堆,实现选择排序。
我们使用小根堆,因此需要一个额外的辅助空间来承载结果(后续它会被我们的优化方案优化掉)。
堆顶出堆后将堆中的最后一个元素赋给堆顶,堆size缩小,然后开始对堆顶执行下沉操作。
int* assist = new int[len];
for (int j = 0; j < len; j++) {assist[j] = arr[0];arr[0] = arr[--size];down(arr,0,size);
}
memcpy(arr, assist, sizeof(int) * len);
delete[] assist;定义pos,
①如果idx节点的左右孩子没有超出数组堆化范围,则pos等于左右孩子中较小的元素的索引,这是为了使得较小的元素总是位于堆的上部。
②如果idx的右孩子超出堆化范围,那么堆中只有左孩子是有效的,pos等于左孩子。
③如果idx的左孩子也超出堆化范围,说明idx已经在堆中沉底,没有后续元素,不必比较直接返回。
当pos位的元素小于idx位的元素时,两者作交换(即idx较大时,与其最小的子节点交换),然后跟踪pos,继续下沉。
void down(int arr[], int idx, int size) {int pos;if (rchild(idx) < size)pos = arr[lchild(idx)] < arr[rchild(idx)] ? lchild(idx) : rchild(idx);else if (lchild(idx) < size)pos = lchild(idx);else return;if (arr[idx] > arr[pos]) {swap(arr[idx], arr[pos]);down(arr,pos,size);}
}Code
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void up(int arr[], int idx) {if (idx && arr[father(idx)] > arr[idx]) {swap(arr[father(idx)], arr[idx]);up(arr, father(idx));}
}
void down(int arr[], int idx, int size) {int pos;if (rchild(idx) < size)pos = arr[lchild(idx)] < arr[rchild(idx)] ? lchild(idx) : rchild(idx);else if (lchild(idx) < size)pos = lchild(idx);else return;if (arr[idx] > arr[pos]) {swap(arr[idx], arr[pos]);down(arr,pos,size);}
}
void heap_sort(int arr[], int len) {int size = 0;for (int i = 0; i < len; i++) {size++;up(arr, i);}int* assist = new int[len];for (int j = 0; j < len; j++) {assist[j] = arr[0];arr[0] = arr[--size];down(arr,0,size);}memcpy(arr, assist, sizeof(int) * len);delete[] assist;
}优化方案
辅助数组assist看起来很愚蠢,我们来像个办法处理掉它。
大根堆优化
我们何不使用大跟堆来依次弹出数组的最大元素呢?
小根堆是从前往后进行最小值选择排序,因此无法安放在原始数组中(因为堆化部分会占据数组的前面部分),但大根堆解决了这个问题。
考虑到弹出时堆size收缩,因此数组的末尾会空出一个位置,我们可以直接将弹出元素安放到该位置上。
Code(pro)
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void bigger_up(int arr[], int idx) {if (idx && arr[father(idx)] < arr[idx]) {swap(arr[father(idx)], arr[idx]);bigger_up(arr, father(idx));}
}
void smaller_down(int arr[], int idx, int size) {int pos;if (rchild(idx) < size)pos = arr[lchild(idx)] > arr[rchild(idx)] ? lchild(idx) : rchild(idx);else if (lchild(idx) < size)pos = lchild(idx);else return;if (arr[idx] < arr[pos]) {swap(arr[idx], arr[pos]);smaller_down(arr, pos, size);}
}
void HPsort(int arr[], int len) {int size = 0;for (int i = 0; i < len; i++,size++) bigger_up(arr, i);while (size--) {swap(arr[0], arr[size]);smaller_down(arr, 0, size);}
}*注意*:大根堆上浮大元素,沉底小元素。
复杂度
时间复杂度:O(nlogn)
空间复杂度:O(logn)
复杂度分析:
时间分析:{
考虑堆化是按层实现的,因此若有n个元素,则有logn层。
对n个元素建堆,每个元素按层上浮,最多比较logn次,得到O(nlogn)
对n个元素出堆,弹出堆顶后将堆尾赋给堆顶,每个元素按层下沉,最多比较logn次,得到O(nlogn)
O(nlogn)+O(nlogn)=O(2nlogn)=O(nlogn)。
}
空间分析:{
使用大跟堆建堆时,不使用额外空间承载答案。
建堆和出堆时调用递归函数进行压栈,函数最多调用logn层,最多占据空间O(logn)。
}
总结
堆为我们提供了一种新的视角来处理数组的最小元素,它的另一个重大用途就是实现优先队列priority_queue。
堆排序的分治策略也比较新颖:他不是在算法思想上进行分治,而是利用模拟堆这种数据结构进行分治,希望可以为你带来对分治思想的新启发。
相关文章:

「数组」堆排序 / 大根堆优化(C++)
目录 概述 核心概念:堆 堆结构 数组存堆 思路 算法过程 up() down() Code 优化方案 大根堆优化 Code(pro) 复杂度 总结 概述 在「数组」快速排序 / 随机值优化|小区间插入优化(C)中,我们介绍了三种基本排序中的冒泡…...

Edegex Foundry docker和源码安装
edgex文档下载 https://github.com/edgexfoundry/edgex-docs/branches/all 在线文档查看 首先要安装python3环境 然后后安装 打开超级终端 #pip3 install mkdocs #mkdocs serve 在浏览器中输入 http://127.0.0.1:8000/edgex-docs/2.3/ 即可打开在线文档 edgex入门可以参考…...

阿里P8和P9级别有何要求
阿里巴巴的P8和P9级别,代表着公司的资深技术专家或管理者岗位,要求候选人具有丰富的职业经历、深厚的技术能力以及出色的领导力。以下是对P8和P9级别的要求、考察点以及准备建议的详细分析。 P8 级别要求 1. 职业经历: 8年以上的工作经验&a…...
【目标检测数据集】锯子数据集1107张VOC+YOLO格式
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):1107 标注数量(xml文件个数):1107 标注数量(txt文件个数):1107 标注…...

移动产业处理器接口(MIPI)协议是什么?
未来汽车的宏伟愿景备受瞩目,特别是驱动这些汽车的技术更是成为焦点。如今,传感器对于汽车视觉和安全技术的下一阶段至关重要,因为驾驶员和乘客都依赖于它们。这些传感器能够支持众多应用,这些应用往往基于人工智能(AI…...
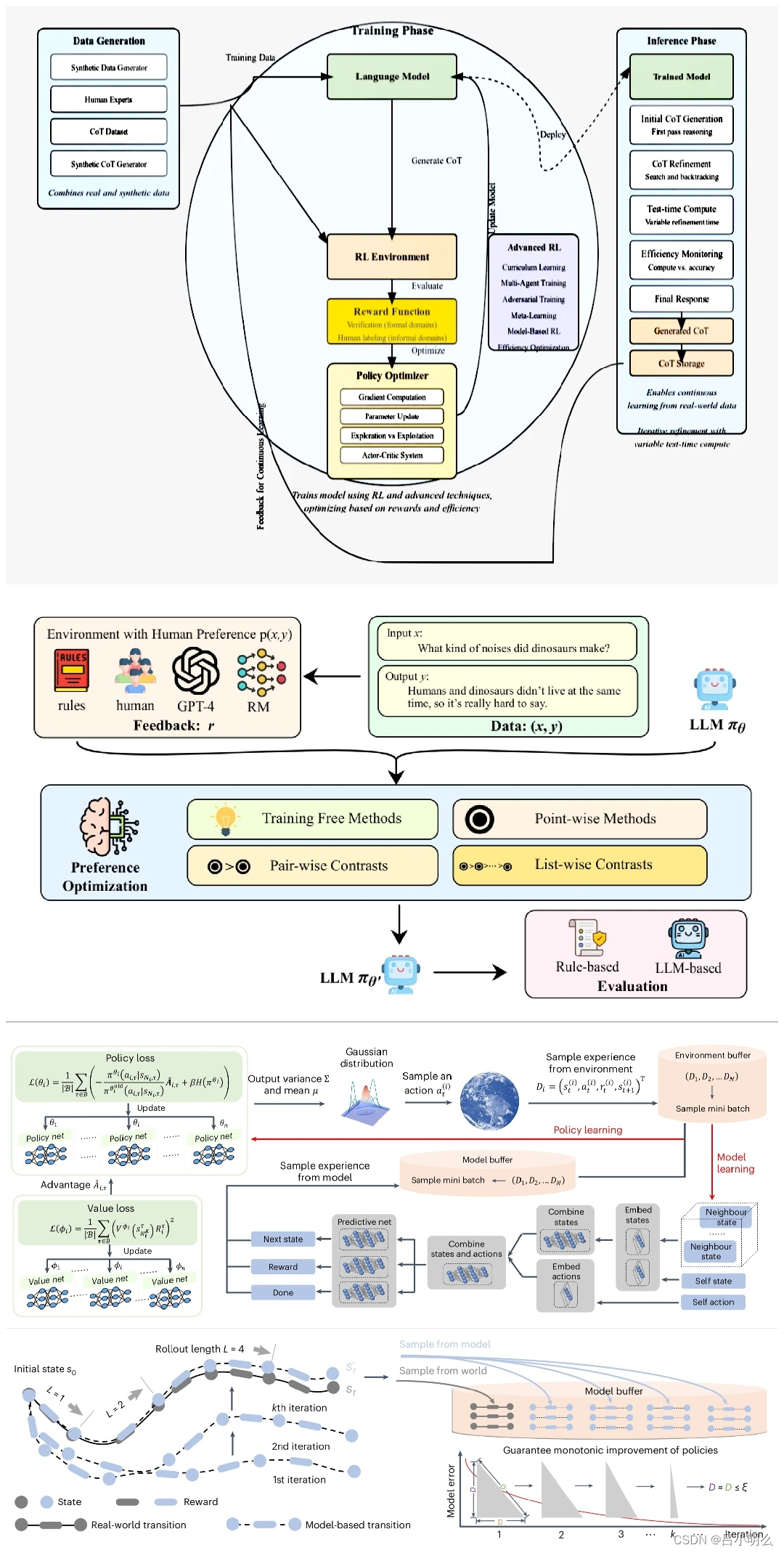
OpenAI o1:隐含在训练与推理间的动态泛化与流形分布
随着OpenAI o1发布,进一步激发了产业与学术各界对AGI的期待以及new scaling law下的探索热情,也看到来自社区和专业机构对o1的阐释,但总感觉还差点什么,因此决定以自己的角度分篇幅梳理下,并分享给大伙: O…...

沉浸式体验和评测Meta最新超级大语言模型405B
2024年7月23日, 亚马逊云科技的AI模型托管平台Amazon Bedrock正式上线了Meta推出的超级参数量大语言模型 - Llama 3.1模型,小李哥也迫不及待去体验和试用了该模型,那这么多参数量的AI模型究竟强在哪里呢?Llama 3.1模型是Meta&…...

Python 课程10-单元测试
前言 在现代软件开发中,单元测试 已成为一种必不可少的实践。通过测试,我们可以确保每个功能模块在开发和修改过程中按预期工作,从而减少软件缺陷,提高代码质量。而测试驱动开发(TDD) 则进一步将测试作为开…...

【嵌入式硬件开发基础】Arduino板常用外设及应用:MPU6050空间运动传感器(简介,类库函数,卡尔曼滤波),继电器(原理介绍,含应用实例/代码)
当一个人不能拥有的时候,他唯一能做的便是不要忘记。 🎯作者主页: 追光者♂🔥 🌸个人简介: 📝[1] CSDN 博客专家📝 🏆[2] 人工智能领域优质创作者🏆 🌟[3] 2022年度博客之星人工智能领域TOP4🌟 🌿[4] 2023年城市之星领跑者TOP1(哈尔滨…...

Pandas Series对象创建,属性,索引及运算详解
目录 Series对象创建 实例化参数 index参数 选用array-like创建Series对象 list ndarray 显示索引与隐式索引 选用dict创建Series对象 不指定索引 指定索引 选用标量创建Series对象 使用标量创建的广播机制 Series属性 name size shape index values Series索…...
优化算法(一)—遗传算法(Genetic Algorithm)附MATLAB程序
遗传算法(Genetic Algorithm, GA)是一种启发式搜索算法,用于寻找复杂优化问题的近似解。它模拟了自然选择和遗传学中的进化过程,主要用于解决那些传统算法难以处理的问题。 遗传算法的基本步骤: 初始化种群࿰…...

高等数学 2.3 高阶导数
一般地,函数 y f ( x ) y f(x) yf(x) 的导数 y ′ f ′ ( x ) y\ f\ (x) y ′f ′(x) 仍然是 x x x 的函数。我们把 y ′ f ′ ( x ) y\ f\ (x) y ′f ′(x) 的导数叫做函数 y f ( x ) y f(x) yf(x) 的二阶导数,记作 y ′ ′ y\ y ′…...

app抓包 chrome://inspect/#devices
一、前言: 1.首先不支持flutter框架,可支持ionic、taro 2.初次需要翻墙 3.app为debug包,非release 二、具体步骤 1.谷歌浏览器地址:chrome://inspect/#devices qq浏览器地址:qqbrowser://inspect/#devi…...

SAP自动化-ME12批量更新某行价格
Python源码 #-Begin-----------------------------------------------------------------#-Includes-------------------------------------------------------------- import sys, win32com.client import os#-Sub Main----------------------------------------------------…...

数据库系统 第58节 概述源码示例
深入探讨数据库技术,我们将通过具体的源代码示例来进一步解释数据库分区、复制、集群和镜像等高级特性。 数据库分区的源代码示例 哈希分区 在PostgreSQL中,可以使用哈希分区来创建一个分区表: CREATE TABLE measurements (city_id …...

软件设计师——程序设计语言
目录 低级语言和高级语言 编译程序和解释程序 正规式,词法分析的一个工具 有限自动机 编辑 上下文无关法 编辑 中后缀表示法 杂题 编辑 低级语言和高级语言 编译程序和解释程序 计算机只能理解由0、1序列构成的机器语言,因此高级程序设计…...

【在Linux世界中追寻伟大的One Piece】五种IO模型和阻塞IO
目录 1 -> 五种IO模型 1.1 -> 阻塞IO(Blocking IO) 1.2 -> 非阻塞IO(Non-blocking IO) 1.3 -> 信号驱动IO(Signal-Driven IO) 1.4 -> IO多路转接(IO Multiplexing) 1.5 -> 异步IO(Asynchronous IO) 2 -> 高级IO概念 2.1 -> 同步通信VS异步通信…...

nginx实现权重机制(nginx基础配置二)
在上一篇文章中我们已经完成了对轮询机制的测试,详情请看轮询机制。 接下来我们进行权重机制的测试 一、conf配置 upstream backServer{ server 127.0.0.1:8080 weight2; server 127.0.0.1:8081 weight1; } server { listen 80; server_name upstream.boyatop.cn…...

华为的仓颉和ArkTS这两门语言有什么区别
先贴下官网: ArkTs官网 仓颉官网 ArkTS的官网介绍说,ArkTS是TypeScript的进一步强化版本,简单来说就是包含了TS的风格,但是做了一些改进。 了解TypeScript的朋友都应该知道,其实TypeScript就是JavaScript的改进版本&…...
DM逻辑备份还原)
(SERIES10)DM逻辑备份还原
1 概念 逻辑备份还原是对数据库逻辑组件(如表、视图和存储过程等数据库对象)的备份还原。逻辑导出(dexp)和逻辑导入(dimp)是 DM 数据库的两个命令行工具,分别用来实现对 DM 数据库的逻辑备份和逻…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
