数组(完全二叉树)向下建堆法与堆排序O(N*logN)
TIPS
AdjustUp & AdjustDown
向上调整AdjustUp与向下调整AdjustDown的参数是一个数组(完全二叉树)+需要进行调整操作的数值的下标/一个数组(完全二叉树)+堆元素个数+需要调整操作的数值的下标。
实际上就是对完全二叉树当中的某一点进行调整直至在其局部范围内满足堆的性质。因此对于完全二叉树如果仅仅对若干个值进行AdjustUp/AdjustDown,并不会是这颗完全二叉树真正变成一个堆。
对于AdjustUp与AdjustDown,在没有任何限制与约束的情况之下,如果说你对数组(完全二叉树)中的某一个元素去进行调整的话,你可以这么做,只不过没有任何意义,因为他最终调整调整,直至在某一个局部范围内满足堆的性质。既然没有任何意义,那它的意义到底是什么呢?AdjustUp与AdjustDown的意义就在于建堆。
那如果说想使用这两个函数往建堆这条正确的方向去走,需要注意:
AdjustUp的前提必须是在child前面数据已经是一个堆;AdjustDown的前提必须是在parent左右两个子树必须是两个堆在这些前提之下,如果说你去AdjustUp与AdjustDown,那么是真正在朝着建堆前进。不然,你在怎么弄的话,只是在局部范围内进行兴风作浪,对于整体并不能使它变成一个堆。
HeapPush & HeapPop
HeapPush与HeapPop的本质与灵魂就是AdjustUp/AdjustDown。这两个的参数分别是一个堆结构体指针+一个需要往堆里面插入的值,一个堆结构体指针。
因此这两个函数的话需要在原先的数组(完全二叉树)就是一个堆的情况下才有意义,不然的话,如果说原先的数组并不是一个堆,那么插入一个数的操作与删除第一个元素意义不大。
数组(完全二叉树)建堆(向下建堆法)O(N)
我们讲过一个建堆方式,就是说是向上调整法建堆,实际上就是不断的插入,如果对于一个数据仅仅进行AdjustUp,只会最终使得局部范围内满足堆的性质,如果说我对数组(完全二叉树)当中的每一个数都进行AdjustUp,那么当我这个操作完了之后,这个数组(完全二叉树)我已经是一个堆了。那有没有其他的方式去建堆呢?
然后我们再进行向下调整法建堆的时候,显而易见的事实就是,我说你对叶子(就是说没有儿子的节点)进行向下调整,那还有什么意义?没有儿子,他调整的也跟白调一样。
所以说向下调整法的话,我需要从倒着往前走,这是第一点(这就为了使得AdjustDown朝着建堆的方向走
并且从倒着往前走之外,我还要从第一个非叶子节点开始进行向下调整。那我该怎么样去找到倒数第一个非叶子节点?我只要把最后一个元素的下标(child)这样((child-1)/2)找到他父亲不就万事大吉了吗?
为什么要倒着走呢?因为倒着走去向下调整的时候,我就可以确保目前这个节点的左右两个子树都已经是堆,这样子的话,我就确保AdjustDown的能够朝着正确的方向(建堆)前进,而不是一直在局部范围内在兴风作浪。
然后向下调整法建堆的话,它的效率比向上调整法建堆要高且差距极大。一般建堆的话是不会用向上调整建堆。

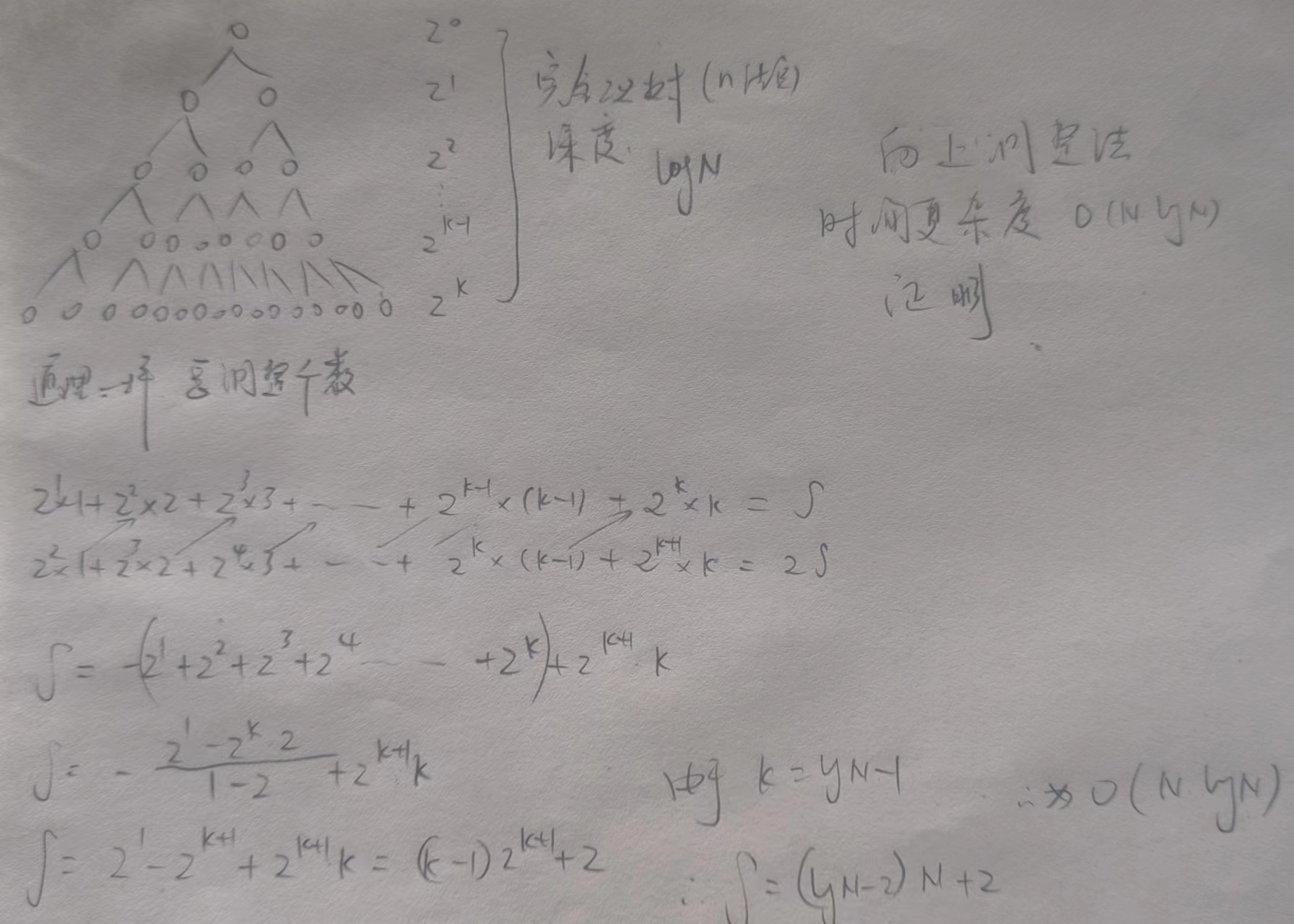
当然,要对数组(完全二叉树)建堆,首先必须得有两个万金油(AdjustUp 与 AdjustDown)
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(int* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){Swap(a + parent, a + child);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void AdjustDown(int* a, int parent, int n)
{assert(a);int child = 2 * parent + 1;while (child<n){if (child+1 <n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(a + parent, a + child);parent = child;child = 2 * parent + 1;}else{break;}}
}演示一下向下调整法建堆
int main()
{int arr[15] = { 1,4,5,2,7,8,3,4,9,0,4,3,11,6,8 };int size = 15;for (int i = (size - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, size);}return 0;
}建堆的核心就在于把AdjustUp与AdjustDown的核心与意义彻底弄清楚
以后建堆就关注这两个: 数组(完全二叉树)得有+AdjustDown核心奥义
堆排序 O(NlogN)
堆在我们这边的优点就是说他已经不像之前那样单独的存储数据,他能够做到帮我们去选数
因此的话,从更加程度而言,它能够帮助我们排序,如果排序的数据量小的话倒还无所谓,我说排序的数据量一大,那么对于性能的要求就非常重要。与我们之前学过的冒泡排序,它的时间复杂度是O(N^2),对堆排序而言的话,它的时间复杂度是O(NlogN)。这两个差异极大
在堆排序之前的话,需要脑子拎清楚的是,我们现在已经不是在堆着那个结构体里面了,现在我们跟手撕数据结构的那个堆就是说自己手搓的那个堆无关了,现在的话相当于就是对题目中给我的数组(完全二叉树)直接进行建堆然后去进行排序。
首先建堆 [ O(N) 向下调整法 ] 数组得有+AdjustDown核心奥义
要对数组(完全二叉树)建堆如果你要升序排列,就要去建大根堆;如果你要降序排列,要去建小根堆,无论是大根还是小根,然后这个数组的顺序确定是从后往前依次慢慢确定下来的。
建堆的向下调整法前面已经讲了
其次调堆 [堆顶与数组末尾开始去倒] AdjustDown核心奥义
当把堆建完之后,接下来就是要去换数据了,这个过程当中的核心核心成员与利器就是AdjustDown,然后每次使用这个函数的时候都需要注意,当前这个堆的数据数量是多少,是每次都要减1减1的哟。
堆排序时间复杂度
堆排序的话,除了一开始要把原始数据(是数组或者说是完全二叉树)建堆之后,还要去转数据调堆。对于第一步,复杂度是O(N)。
然后调堆的时间复杂度也是logN*N,用错位相减法减减算算也很快的,或者说你用直观的方法去看一下,对于最后一层而言,如果说你想要确定最后一层(堆排序的话,它是确定的顺序是从数组的从后往前慢慢确定下来的),要确定最后一层的话,就需要不断的把堆顶的数据给往下调整,这就相当于就是说节点最多的层数,它需要调整的次数也是最多。
因此对于堆排序而言的话,就是说你在一开始对数组(完全二叉树)建堆的时候,无论是用什么方法去建堆,最后总的堆排序时间复杂度都是O(N*logN)
代码
int main()
{int arr[10] = { 1,4,3,5,7,9,8,6,2,0 };int size = 10;//建堆for (int i = (size - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, size);}//调堆int end = size - 1;while (end > 0){Swap(arr + 0, arr + end);AdjustDown(arr, 0, end);end--;}return 0;
}你会发现,在堆排序里面无论是建堆还是调堆,都与AdjustUp无关
相关文章:
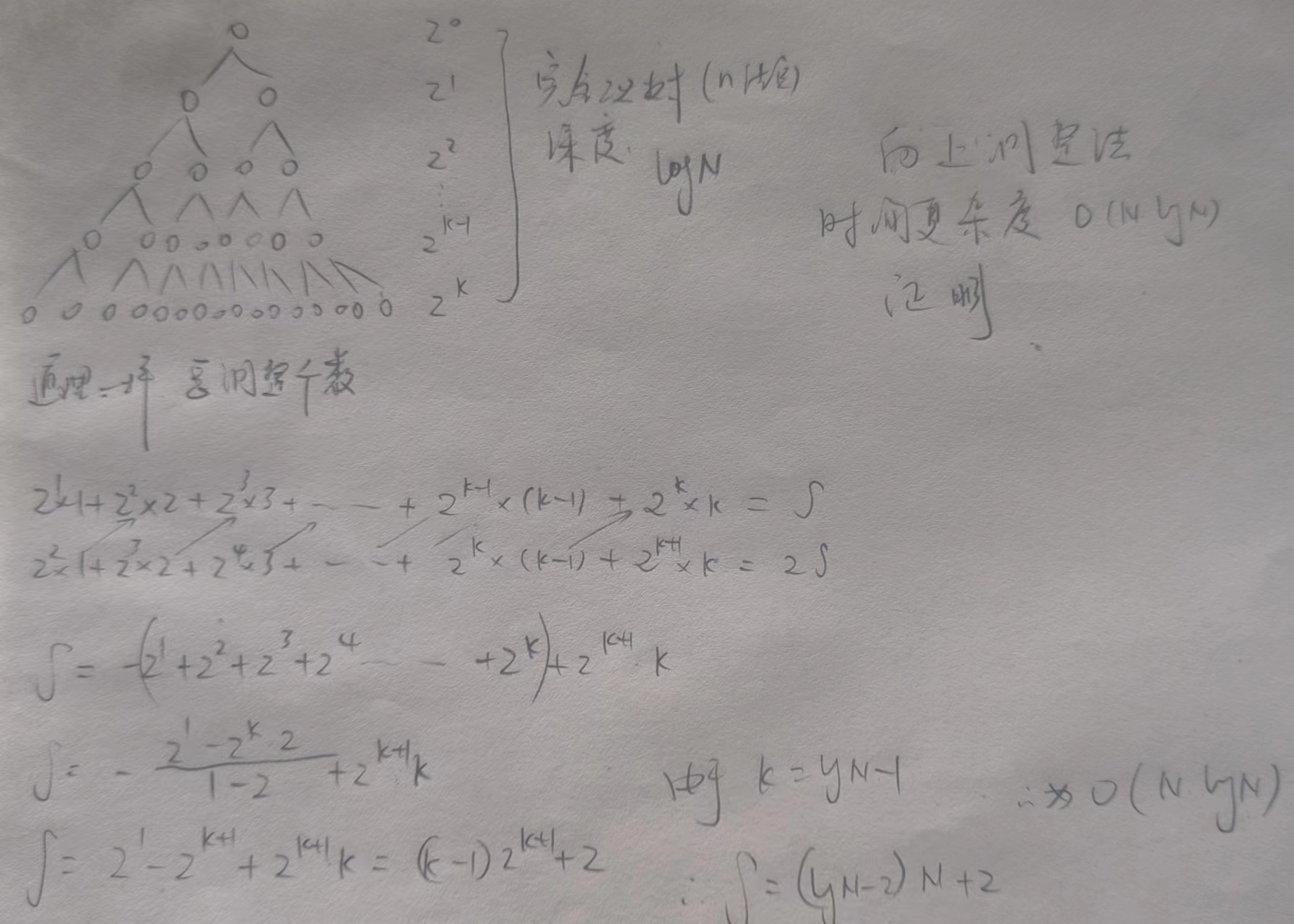
数组(完全二叉树)向下建堆法与堆排序O(N*logN)
TIPS AdjustUp & AdjustDown向上调整AdjustUp与向下调整AdjustDown的参数是一个数组(完全二叉树)需要进行调整操作的数值的下标/一个数组(完全二叉树)堆元素个数需要调整操作的数值的下标。实际上就是对完全二叉树当中的某一点…...

Lua require 函数使用
从 Lua 的用户文档中我们知道 require("modName") 函数是用来加载模块的,而如果这个modName已经用require 加载过的,再调用require时,将直接返回模块的值。因为函数首先查找 package.loaded 表, 检测 modName 是否被加载…...
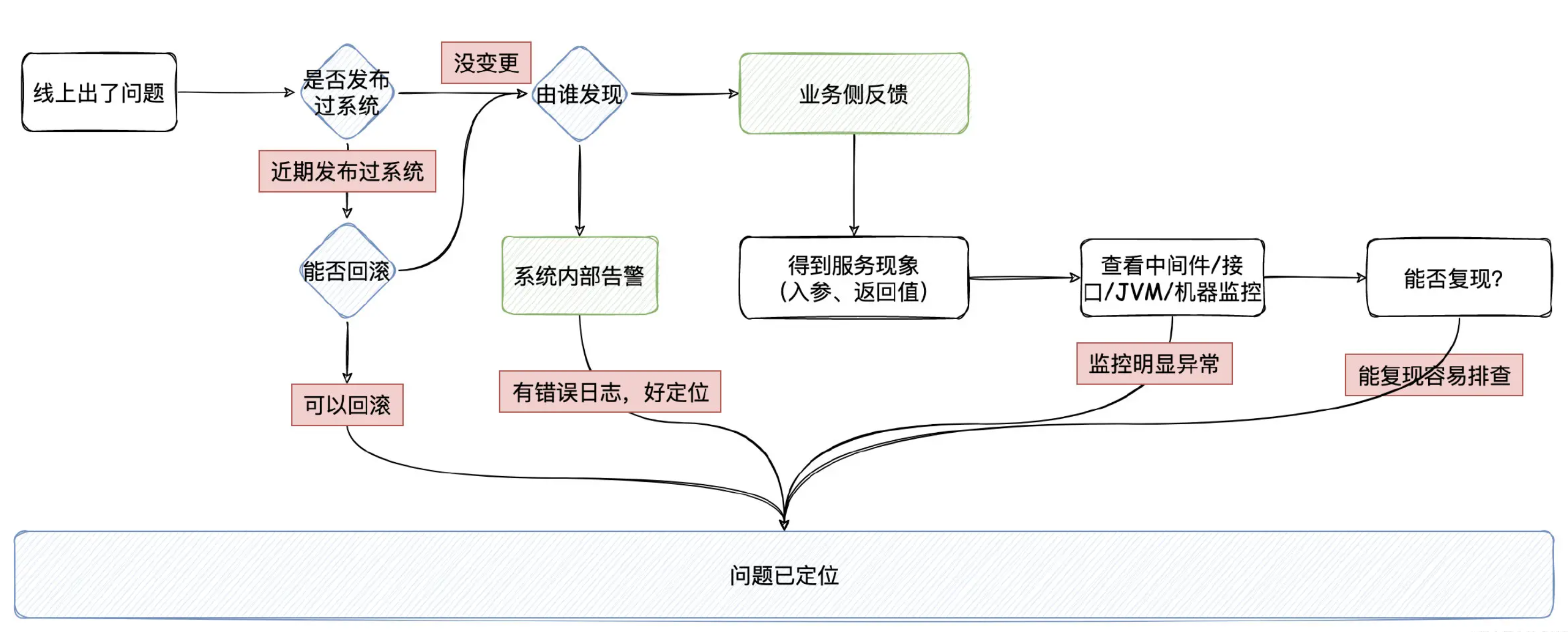
【面试】如何定位线上问题?
这个面试题我在两年社招的时候遇到过,前几天面试也遇到了。我觉得我每一次都答得中规中矩,今天来梳理复盘下,下次又被问到的时候希望可以答得更好。 下一次我应该会按照这个思路去答: 1、如果线上出现了问题,我们更多…...

字节二面,原来我对自动化测试的理解太浅了
如果你入职一家新的公司,领导让你开展自动化测试,作为一个新人,你肯定会手忙脚乱,你会如何落地自动化测试呢? 01 什么是自动化 有很多人做了很长时间的自动化但却连自动化的概念都不清楚,这样的人也是很悲…...

Android11.0 应用升级成功后立即断电重启,版本恢复
问题:客户反馈内置的应用升级成功后立刻断电重启,应用的版本被恢复。 使用adb命令升级客户应用,查看版本显示已更新,/data/system目录下packages.xml和packages.xml中应用版本信息均已更新 C:\Users\dell>adb shell dumpsys …...

关于python常用软件用法:Pycharm 常用功能
人生苦短,我用python 一.Pycharm的基本使用 1.在Pycharm下为你的Python项目配置Python解释器 (1).Setting>Project Interpreter>源码资料电子书:点击此处跳转文末名片获取 二.在Pycharm下创建Python文件、Python模块 1.File>New&g…...

SOLIDWORKS你不知道的小技巧
◉ SOLIDWORKS圆弧长度标注点智能标注,再选中该圆弧,然后分别点圆弧的两个端点,点击左键可以标注圆弧长度。◉ SOLIDWORKS强力裁剪剪裁实体中的强劲剪裁,除了可以裁剪实体外,还可以任意延伸实体。◉ SOLIDWORKS转折线转…...

有了HTTP,为啥还要用RPC
既然有 HTTP 请求,为什么还要用 RPC 调用? 一直以来都没有深究过RPC和HTTP的区别,不都是写一个服务然后在客户端调用么? HTTP和RPC最本质的区别,就是 RPC 主要是基于 TCP/IP 协议的,而 HTTP 服务主要是基…...

[leetcode] 动态规划
背包 先啃懂 背包九讲 01背包,即物品有限。 for 物品for 容量(倒序)P1048 [NOIP2005 普及组] 采药 [ 原题 | 题解 ] P1049 [NOIP2001 普及组] 装箱问题 [ 原题 | 题解 ] P1507 NASA的食物计划 [ 原题 | 题解 ] P1510 精卫填海 [ 原题 | 题…...
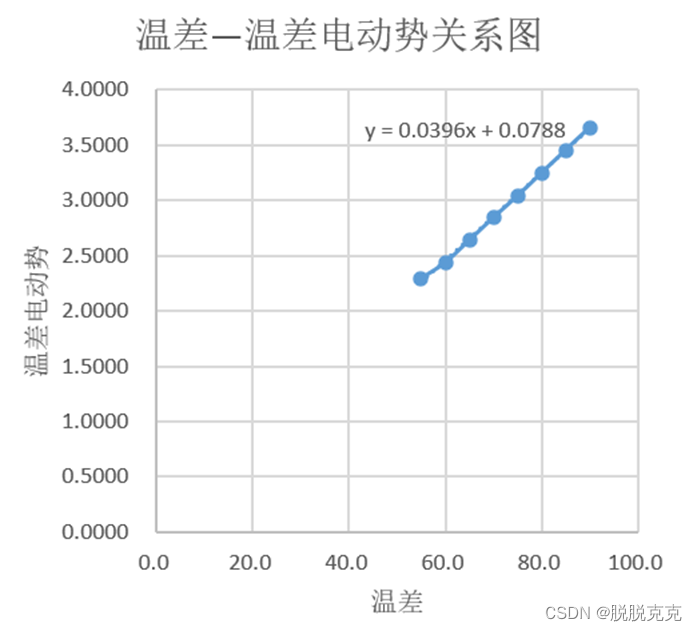
科大奥瑞物理实验——热电偶特性及其应用研究
实验名称:热电偶特性及其应用研究 1. 实验目的: 掌握电位差计的工作原理和结构特点;了解温差电偶测温的原理和方法;学会电位差计的使用及注意事项。 2. 实验器材: 电位差计 标准电池 光电检流计 稳压电源 温差电偶…...
)
Eclips快捷键大全(超详细)
Eclips快捷键大全(超详细)前言一、常用快捷键二、编辑快捷键三、导航快捷键四、运行和调试快捷键五、重构快捷键六、代码生成快捷键七、项目导航快捷键八、帮助快捷键九、搜索快捷键十、标记快捷键十一、版本控制快捷键十二、其它快捷键前言 本博主将用C…...
整懵了,蚂蚁金服4面成功拿下测开offer,涨薪10k,突然觉得跳槽也不是那么难
蚂蚁的面试挺独特的,每轮面试都没有HR约时间,一般是晚上8点左右面试官来一个电话,问是否能面试,能的话开始面,不能就约一个其他时间。 全程4面,前四面技术面,电话面试,最后一面是HR面…...

C++内存分布malloc-free-new-delete的区别和联系
目录 一、内存分布 1.1内存分布图: 1.2 为什么要将bss和data区分开呢? 1.3 堆和栈有什么区别 二、malloc、free;new、delete 2.1 new和delete是如何实现的,new与malloc的异同处 2.2既然有了malloc/free,C为什么还…...
)
【华为OD机试 2023最新 】 最多颜色的车辆(C++ 100%)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 在一个狭小的路口,每秒只能通过一辆车,假设车辆的颜色只有 3 种,找出 N 秒内经过的最多颜色的车辆数量。 三种颜色编号为0 ,1 ,2 输入描述 第一行输入的是通过的车辆颜色信息 [0,1,1,2] 代表4 秒钟通过的车…...

Linux安全加固
一、重要文件 /etc/passwd #记录本地用户的属性信息,如UID、GID /etc/shadow #存放用户的口令信息 只有系统管理员能查看 /etc/pam.d/system-auth #账户安全配置文件 /etc/login.defs #修改登录的配置文件 /etc/profile …...

Java基础学习(6)
Java基础学习一 字符串1.1 API 与 API文档1.1.1 如何使用帮助文档查找想要导用的方法1.2 String 概述1.3 创建String对象的两种方式第一种第二种1.4 Java常用字符串方法1.4.1 比较1.4.2 字符串通过索引取出1.4.3 取出字符串中的单个字符1.4.4 替换出字符串当中的字符1.4.5 取出…...

【LeetCode】链表练习 9 道题
第一题:移除链表元素 题目描述: 给你一个链表的头节点head和一个整数val,请你删除链表中所有满足Node.val val的节点,并返回新的头节点 。 列表中的节点数目在范围 [0, 10^4] 内1 < Node.val < 500 < val < 50 /…...

轴承远程监控系统解决方案
一、项目背景 随着现代机械设备朝着高集成、高精密度、系统化、自动化的方向发展,在工业生产中一旦机器发生故障,即使局部失灵,都可能导致设备工作失效,甚至造成整个自动化车间停产,从而给工业生产带来巨大的损失。轴承…...

阿里云轻量服务器Workbench root远程连接和一键连接的区别
阿里云轻量应用服务器远程连接支持Workbench root用户连接和Workbench一键连接,Workbench root需要输入root密码,一键连接不需要输入密码,但是也无法获得root权限,阿里云百科来详细说下阿里云轻量应用服务器远程连接说明ÿ…...
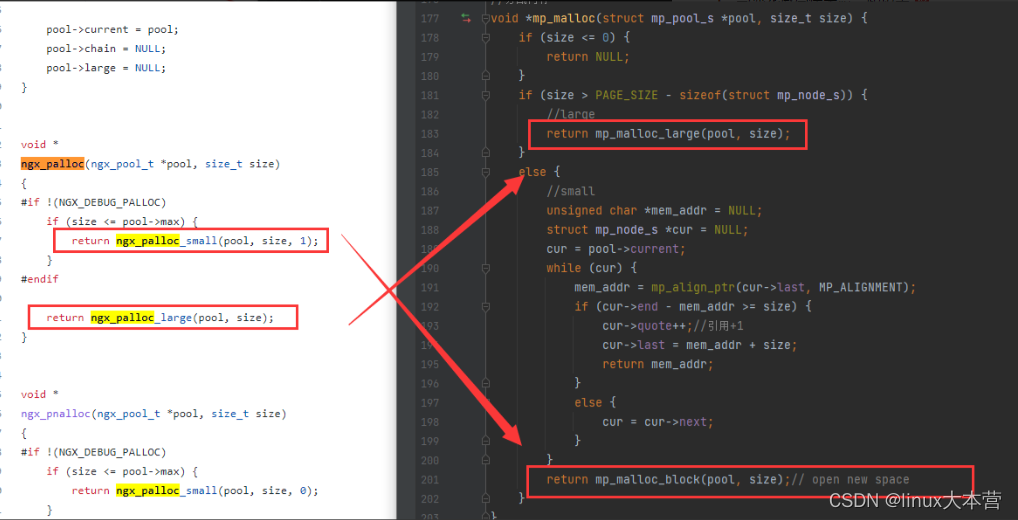
带你用纯C实现一个内存池(图文结合)
为什么要用内存池 为什么要用内存池?首先,在7 * 24h的服务器中如果不使用内存池,而使用malloc和free,那么就非常容易产生内存碎片,早晚都会申请内存失败;并且在比较复杂的代码或者继承的屎山中,…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
