力扣题解2848
大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述(简单):
与车相交的点
给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] = [starti, endi] ,其中 starti 是第 i 辆车的起点,endi 是第 i 辆车的终点。
返回数轴上被车 任意部分 覆盖的整数点的数目。


解题思路:
这道问题抽象就抽象在,读不懂题目要求干啥,也不明白举例是什么意思,得先把题目看懂。(我来中译中一下)
这个问题可以理解为在数轴上有多辆车,每辆车的停车区域用一个区间来表示,例如 nums[i] = [starti, endi] 表示第 i 辆车的起点为 starti,终点为 endi。我们需要计算在数轴上这些车的停车区域重叠部分所覆盖的整数点的总数。
具体来说,我们需要求出所有车辆停车区间内的整数点的总和,即使得某一点被多辆车的区间覆盖也只算一次。
示例说明:
假设车辆的区间如下:
-
车1: [1, 3]
-
车2: [2, 5]
-
车3: [4, 6]
那么这些车辆覆盖的区间为:
-
车1覆盖的整数点为 {1, 2, 3}
-
车2覆盖的整数点为 {2, 3, 4, 5}
-
车3覆盖的整数点为 {4, 5, 6}
所有被覆盖的整数点为 {1, 2, 3, 4, 5, 6},所以被覆盖的整数点总数为 6。
算法思路:
-
合并区间:首先对所有区间进行合并,去掉重叠部分。
-
计算被覆盖的点:在合并之后计算每个区间中整数点的数量,即为 end - start + 1 的总和。
3.采用排序加贪心策略
参考代码:
// 定义一个结构体来表示区间
typedef struct {int start;int end;
} Interval;
// 比较函数用于排序
int compare(const void *a, const void *b) {Interval *intervalA = (Interval *)a;Interval *intervalB = (Interval *)b;return intervalA->start - intervalB->start;
}
int numberOfPoints(int** nums, int numsSize, int* numsColSize) {if (numsSize == 0) return 0;
// 1. 创建一个 Interval 数组Interval* intervals = (Interval*)malloc(numsSize * sizeof(Interval));
// 2. 将 nums 转换为 Interval 数组for (int i = 0; i < numsSize; i++) {intervals[i].start = nums[i][0];intervals[i].end = nums[i][1];}
// 3. 排序区间qsort(intervals, numsSize, sizeof(Interval), compare);
int totalPoints = 0;int currStart = intervals[0].start;int currEnd = intervals[0].end;
// 4. 合并区间并计算覆盖的点for (int i = 1; i < numsSize; i++) {if (intervals[i].start <= currEnd) { // 如果有重叠// 扩大当前区间的结束点if (intervals[i].end > currEnd) {currEnd = intervals[i].end;}} else { // 如果没有重叠,计算当前区间的点数totalPoints += currEnd - currStart + 1;currStart = intervals[i].start;currEnd = intervals[i].end;}}
// 添加最后一个区间的覆盖点totalPoints += currEnd - currStart + 1;
// 释放内存free(intervals);
return totalPoints;
}
时间复杂度:
1. 创建 Interval 数组:
创建 Interval 数组的时间复杂度是 O(n),其中 n是输入的区间数量 `numsSize`。
2. 将 nums 转换为 Interval 数组:
遍历所有区间并将其转换为 Interval 的时间复杂度同样是 O(n)。
3. 排序区间:
使用 `qsort` 进行排序,排序的时间复杂度是 O(n log n)。
4. 合并区间并计算覆盖的点:
遍历排好序的区间以合并并计算覆盖点的时间复杂度是 O(n)。
综上所述,主要的时间开销在于排序,因此整个 `numberOfPoints` 函数的时间复杂度为:
[O(n log n)]
空间复杂度:
1. 存储 Interval 数组:
创建存储 Interval 的数组需要 O(n)的额外空间。
2. 其他空间:
在函数中使用的变量、指针等只占用常数空间 O(1),不随 n 的变化而变化。
因此,整个函数的空间复杂度主要依赖于存储 Interval 数组的开销,为:
[O(n)]
总结:
时间复杂度:(O(n log n))
空间复杂度:(O(n))
相关文章:

力扣题解2848
大家好,欢迎来到无限大的频道。 今日继续给大家带来力扣题解。 题目描述(简单): 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] &…...

电子电气架构---智能汽车应该是怎么样的架构?
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不…...

无心剑七绝《中秋相思》
七绝中秋相思 中秋月满意深长 百代江阳老窖香 莫道天涯情不尽 相思寸寸赋华章 2023年9月29日 平水韵七阳平韵 这首诗七绝《中秋相思》由无心剑所作,以其深情的笔触描绘了中秋夜的相思之情。 诗中首句“中秋月满意深长”即以中秋圆月为起点,勾勒出了一幅…...

Python画笔案例-051 绘制赵爽弦图
1、绘制赵爽弦图 通过 python 的turtle 库绘制 赵爽弦图,如下图: 2、实现代码 绘制 赵爽弦图,以下为实现代码: """赵爽弦图.py本程序演录了如何自定义形状,如何把它添加到造型字典。赵爽弦图是用来证明…...

SEGGERS实时系统embOS推出Linux端模拟器
SEGGER 发布了两个新的 embOS 仿真模拟器:embOS Sim Linux 和 embOS-MPU Sim Linux。 通过模拟 Linux 主机系统上的硬件,取代物理硬件,为开发人员提供了一种无缝的方式来构建原型和测试应用程序。 embOS Sim Linux 端口支持 32 位和 64 位系…...

HTML + CSS - 网页布局之一般布局浮动布局
1. 一般布局 1.1 一般布局相关参数 元素内容常常可以想像为放在一个盒子里,然后在周边加上内边距,边框和外边距,是盒子模型 默认一个块级区域会填充父类所有的行向空间,并且沿着块伸长容纳其内容,可以为块状体设置某…...

python定时任务,定时爬取水质和天气
定时爬取水质和天气 代码 代码 from apscheduler.schedulers.background import BackgroundScheduler import requests import datetimeurlweather "http://localhost:8000/CrwalingViewWeather" # 天气接口 urlwater "http://localhost:8000/CrwalingViewW…...

ARM驱动学习之基础小知识
ARM驱动学习之基础小知识 • sch原理图工程师工作内容 – 方案 – 元器件选型 – 采购(能不能买到,价格) – 原理图(涉及到稳定性) • layout画板工程师 – layout(封装、布局,布线,…...

【字幕】恋上数据结构与算法之019动态数组07打印数组
是吧?什么意思呢?你看啊我们刚刚已经加了三个东西了,我现在希望能够打印一下这个速度,希望能把它里面所有元素打出来,那我们试一下,看它默认是怎么打,这个时候我们右击你会发现它打出来长这样子…...

Python基础语法(3)下
列表和元组 列表是什么,元组是什么 编程中,经常需要使用变量,来保存/表示数据。变量就是内存空间,用来表示或者存储数据。 如果代码中需要表示的数据个数比较少,我们直接创建多个变量即可。 num1 10 num2 20 num3…...
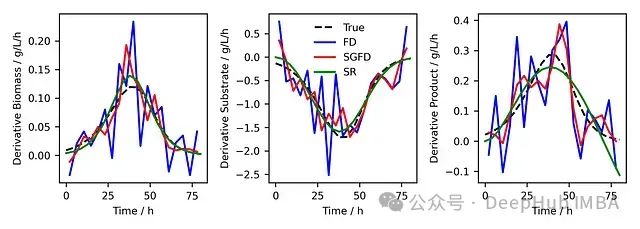
数据稀缺条件下的时间序列微分:符号回归(Symbolic Regression)方法介绍与Python示例
时间序列概况在日常生活和专业研究中都很常见。简而言之,时间序列概况是一系列连续的数据点 y(0), y(1), …, y(t) ,其中时间 t 的点依赖于时间 t-1 的前一个点(或更早的时间点)。 在许多应用中,研究者致力于预测时间序列概况的未来行为。存在各种建模方法。这些模型通常基于过…...
XML_Tomcat_HTTP
第四章 XML_Tomcat10_HTTP 一 XML XML是EXtensible Markup Language的缩写,翻译过来就是可扩展标记语言。所以很明显,XML和HTML一样都是标记语言,也就是说它们的基本语法都是标签。 可扩展 三个字表面上的意思是XML允许自定义格式。但这不代…...

GPT Prompt
Reference https://help.openai.com/en/articles/6654000-best-practices-for-prompt-engineering-with-the-openai-apihttps://platform.openai.com/docs/guides/prompt-engineeringbilibili 8分钟系统学习提示工程,别再说大模型还不够聪明!Prompt Engineering,提示词,Few…...

go基础知识归纳总结
无缓冲的 channel 和有缓冲的 channel 的区别? 在 Go 语言中,channel 是用来在 goroutines 之间传递数据的主要机制。它们有两种类型:无缓冲的 channel 和有缓冲的 channel。 无缓冲的 channel 行为:无缓冲的 channel 是一种同步…...

【字幕】恋上数据结构与算法之014动态数组02接口设计
申请表数组英文单词叫away,而这个数组是怎么样的申请表?数组是一种顺序存储的申请表,什么叫顺序存储?就是数组里面的所有元素,它的内存地址是连续的,大家的内存是连续的,比如说举个例子…...

ffmpeg硬件解码一般流程
流程 根据硬件名称,查询是否是支持的类型 const char *device_name "qsv"; //cuda enum AVHWDeviceType type av_hwdevice_find_type_by_name(device_name); if(type AV_HWDEVICE_TYPE_NONE) {//如果一个硬件类型是不支持的,打印所有支持…...

微信支付开发-程序开发
一、操作流程图 二、后端代码实现 1、题库实现 a、列表、所有、详情、保存、启禁用、导入答题 b、获取奖品信息、保存奖品信息、 class Question extends Base {// 列表public function getList(){$param $this->request->param();$where [];if(!empty($param[title])…...

【数据结构】排序算法系列——堆排序(附源码+图解)
堆排序 堆排序基于一种常见的**[[二叉树]]结构**:堆 我们前面讲到选择排序,它在待排序的n个记录中选择一个最小的记录需要比较n一1次。本来这也可以理解,查找第一个数据需要比较这么多次是正常的,否则无法知道它是最小的记录。 …...

Linux——应用层自定义协议与序列化
目录 一应用层 1再谈 "协议" 2序列化与反序列化 3理解read,write,recv,send 4Udp vs Tcp 二网络版本计算器 三手写序列和反序列化 四进程间关系与守护进程 1进程组 1.1什么是进程组 1.2组长进程 2会话 2.1什么是会话 2.2会话下的前后台进程 3作业控…...

CGAL 从DSM到DTM-建筑物区域提取
CGAL 从DSM到DTM-建筑物区域提取 生成的DSM被用作DTM计算的基础,即地面表示为过滤掉非地面点后的另一个TIN。主要是去除一些建筑物和植被非地形点。 建筑物立面及连通区域提取 建筑物立面的特征是三角形面片的高度变化剧烈。 通过遍历每一个三角面片,…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
