模式识别 —— 第六章 支持向量机(SVM)与核(Kernel)
模式识别 —— 第六章 支持向量机(SVM)与核(Kernel)
文章目录
- 模式识别 —— 第六章 支持向量机(SVM)与核(Kernel)
- 硬间隔(Hard-Margin)
- 软间隔(Soft-Margin)
- 核kernel
- 对偶问题
- 硬间隔优化问题的对偶转变
- 考点
- 软间隔优化问题的对偶转变
开始之前先推荐一个个人感觉把SVM讲的特别好的课程视频(尤其是转对偶问题那一部分),浙大胡浩基老师手写板书讲的,真的草履虫都能看懂!
点一下 嗖~就过去
硬间隔与软间隔区别如下:
硬间隔
完全分类准确,只在数据是线性可分离的时候才有效。其损失函数不存在,损失值为0。但它对异常值非常敏感,无法很好的泛化。
软间隔
要避免这些问题,最好使用更灵活的模型。目标是尽可能在保持最大间隔宽度和限制间隔违例之间找到良好的平衡,这就是软间隔分类。
所以软间隔允许一定量的样本分类错误;优化函数包括两个部分,一部分是点到平面的间隔距离,一部分是误分类的损失个数;C是惩罚系数,误分类个数在优化函数中的权重值;权重值越大,误分类的损失惩罚的越厉害。
硬间隔(Hard-Margin)
我们想找到一个超平面让其线性可分,数学表述如下:

a式子与b式子合并可得到下面的统一表示。
现在我们想让在这个分界线(面)附近的点(即支持向量)离它尽量远一点。由点到直线距离公式来使得Margin最大。
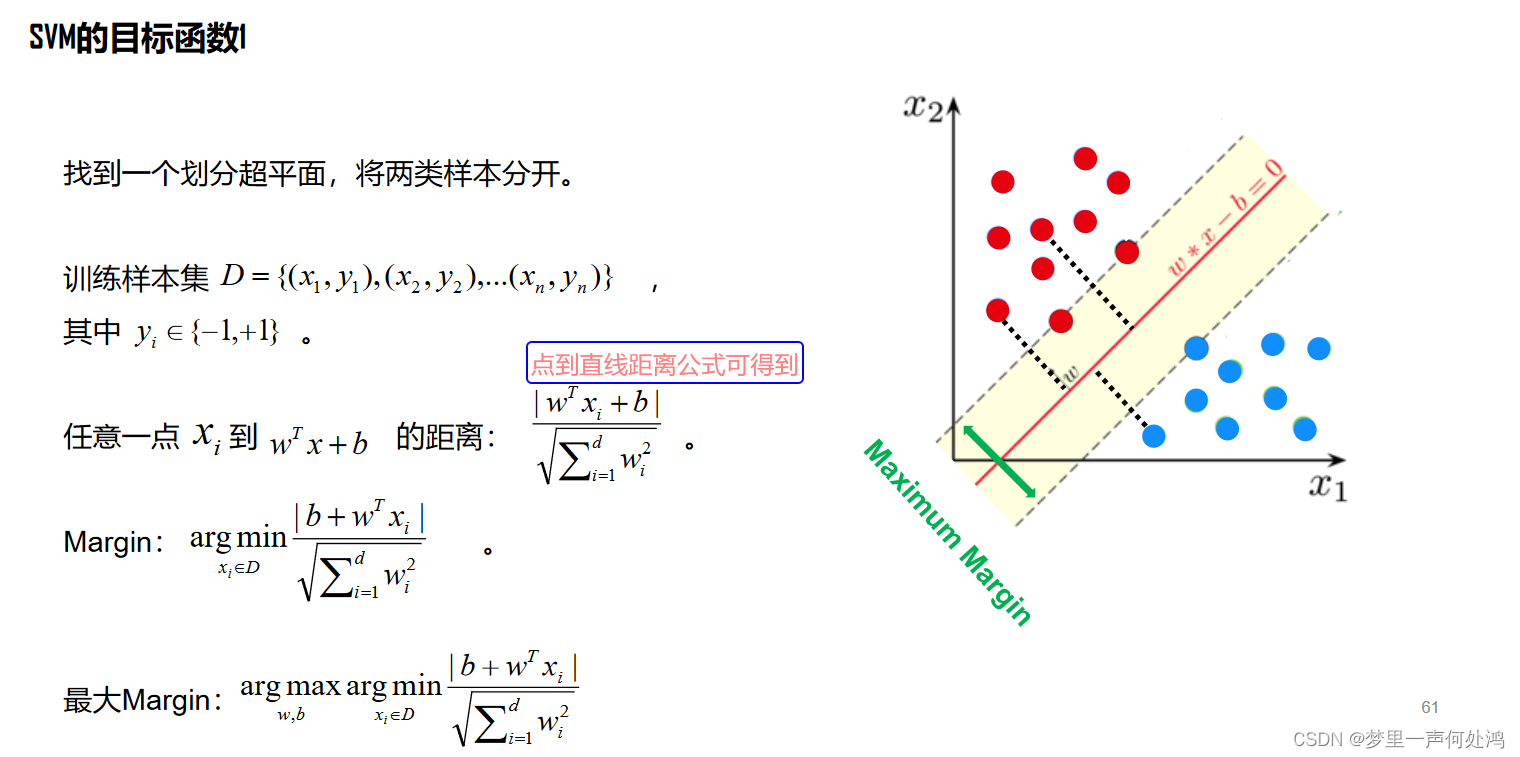
然后我们想办法将最大化Margin转化为下面这个优化问题:

怎么转化的呢?首先我们有两个事实条件:

之后:

此时,对于非支持向量那就相当于∣wTx0+b∣>1\lvert w^Tx_0+b \rvert >1∣wTx0+b∣>1
把y写进去来代替绝对值符号的作用就可以得到新的限制条件y(wTx0+b)≥1y(w^Tx_0+b) \geq 1y(wTx0+b)≥1
最后我们为了后续求导方便,我们可以在目标函数处多加一个12\frac{1}{2}21,如下:
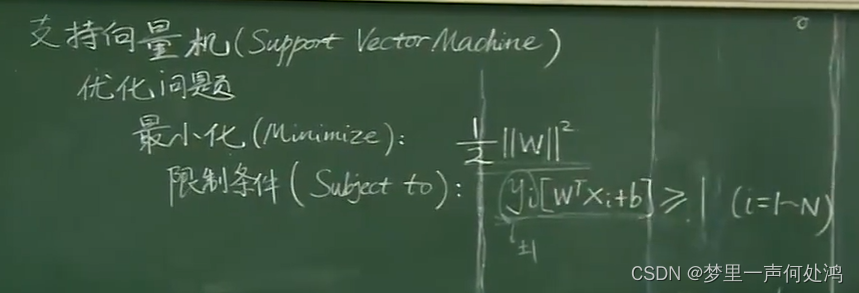
这样就变成了一个凸优化的问题,即要么无解、要么只有一个极值。因此局部极值就是最值。
软间隔(Soft-Margin)

SVM对训练集里面的每个样本(xi,yi)(x_i,y_i)(xi,yi)引入了一个松弛变量ξi≥0ξ_i≥0ξi≥0,使函数间隔加上松弛变量大于等于1,也就是说条件变量改为如下:
yi(w∙xi+b)≥1−ξiyi(w∙xi+b)≥1−ξiyi(w∙xi+b)≥1−ξi
加入松弛变量ξiξ_iξi后,损失函数就需要改写为:
min12∣∣wi∣∣2+C∑i=1nξimin\frac12||w_i||^2+C\sum_{i=1}^nξ_imin21∣∣wi∣∣2+Ci=1∑nξi
s.t.yi(wTxi+b)≥1−ξi(i=1,2,...m)s.t. \quad y_i(w^Tx_i+b)≥1−ξ_i(i=1,2,...m)s.t.yi(wTxi+b)≥1−ξi(i=1,2,...m)
ξi≥0(i=1,2,...m)ξ_i≥0(i=1,2,...m)ξi≥0(i=1,2,...m)
这里,C>0为惩罚参数,可以理解为我们一般回归和分类问题正则化时候的参数。C越大,对误分类的惩罚越大,C越小,对误分类的惩罚越小。
也就是说,我们希望12∣∣wi∣∣2\frac12||w_i||^221∣∣wi∣∣2尽量小,误分类的点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中,需要调参来选择。
核kernel
对于在低维线性不可分的数据,在映射到了高维以后,就变成线性可分的了。例如:
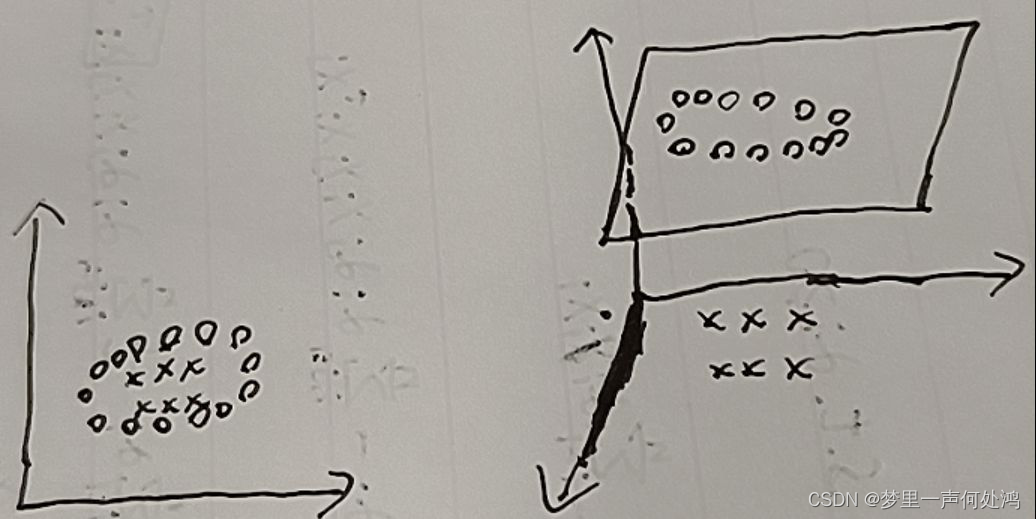
左边是在二维空间的投影,我们没办法找到一条直线将两个类别区分开。但是如果我们将二维空间映射到三维空间的话,我们就可以找到一个超平面在三维中线性可分。
就像是三体中狄奥伦娜能进入四维空间后轻易的取人脑子一样。
维度越高线性可分就越容易。但是映射成的高维维度是爆炸性增长的,这个计算量实在是太大了,而且如果遇到无穷维的情况,就根本无从计算了。这就要用到我们的核函数了。
核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数好在它在低维上进行计算,而将实质上的分类效果(利用了内积)表现在了高维上,这样避免了直接在高维空间中的复杂计算,真正解决了SVM线性不可分的问题。
线性核函数
线性核函数(Linear Kernel)其实就是內积,如下:
K(x,y)=x∙yK(x,y)=x∙yK(x,y)=x∙y
多项式核函数
多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,公式如下:
K(x,y)=(γx∙y+r)dK(x,y)=(γx∙y+r)^dK(x,y)=(γx∙y+r)d
高斯核函数
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。公式如下:
K(x,y)=e−∣∣x−y∣∣22σ2K(x,y)=e^{-\frac{||x-y||^2}{2\sigma ^2}}K(x,y)=e−2σ2∣∣x−y∣∣2
对偶问题
这部分建议看视频部分的讲解,讲的真的超级棒!
这里我们采用的是拉格朗日乘子将其转化成对偶问题,思路如下:

硬间隔优化问题的对偶转变
按照上述思路,首先我们将限制条件转换成a(x)≤0a(x) \leq 0a(x)≤0的形式:
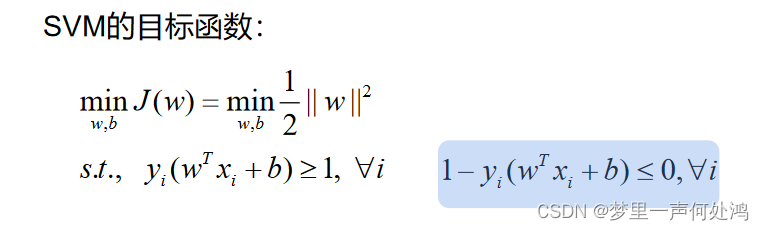
之后我们构建拉格朗日常数:

因为是求最值,所以我们求导进行回代:

考点
这是我们这学期的期末考试题,老师提前透露的。也是类似上面的推导,只不过要简单一点再。
就是如果目标函数不是wTxi+bw^Tx_i + bwTxi+b而是wTxiw^Tx_iwTxi,请进行对偶问题的转换。其实是变简单了,不用对b进行求导回代了。解法如下:

可恶啊,背面画着图透过来了。算了,凑合看吧,其实结果是一样的。
软间隔优化问题的对偶转变
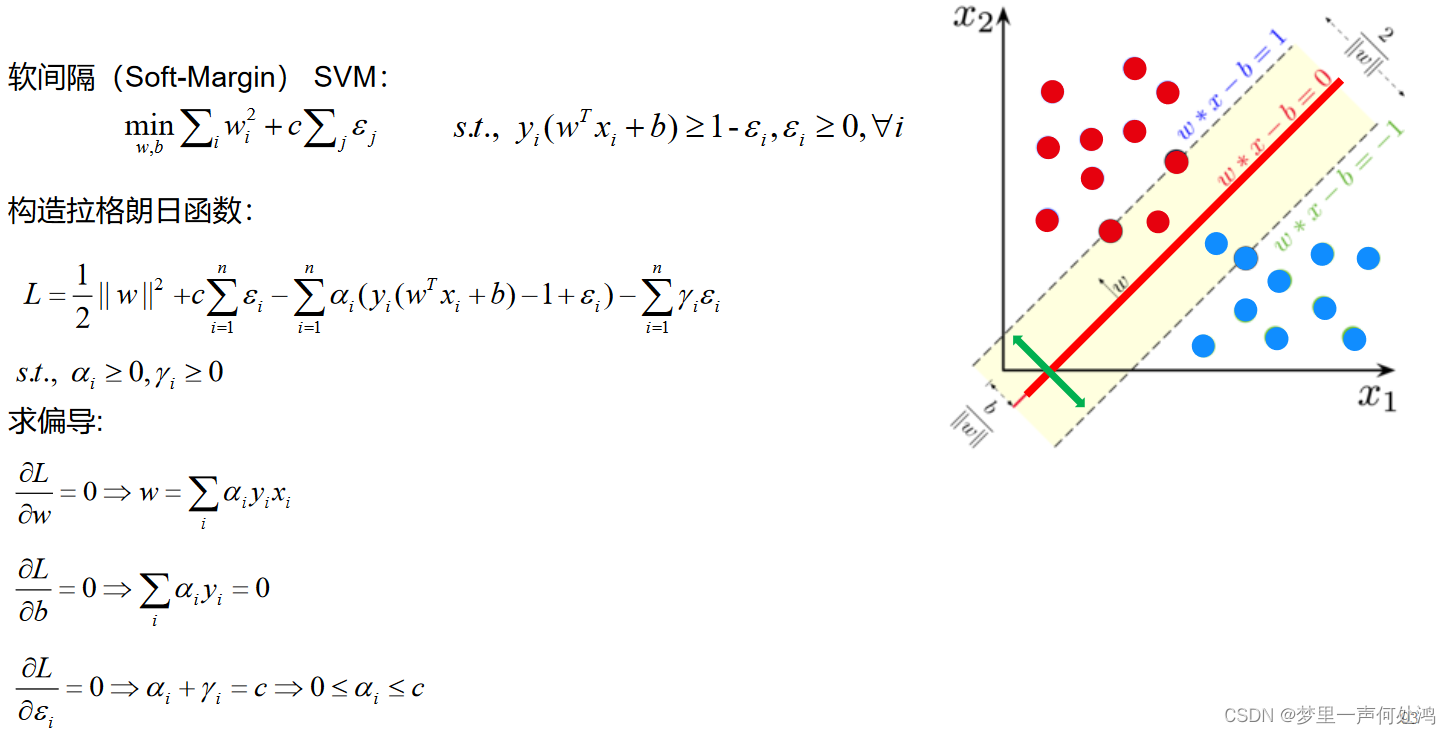
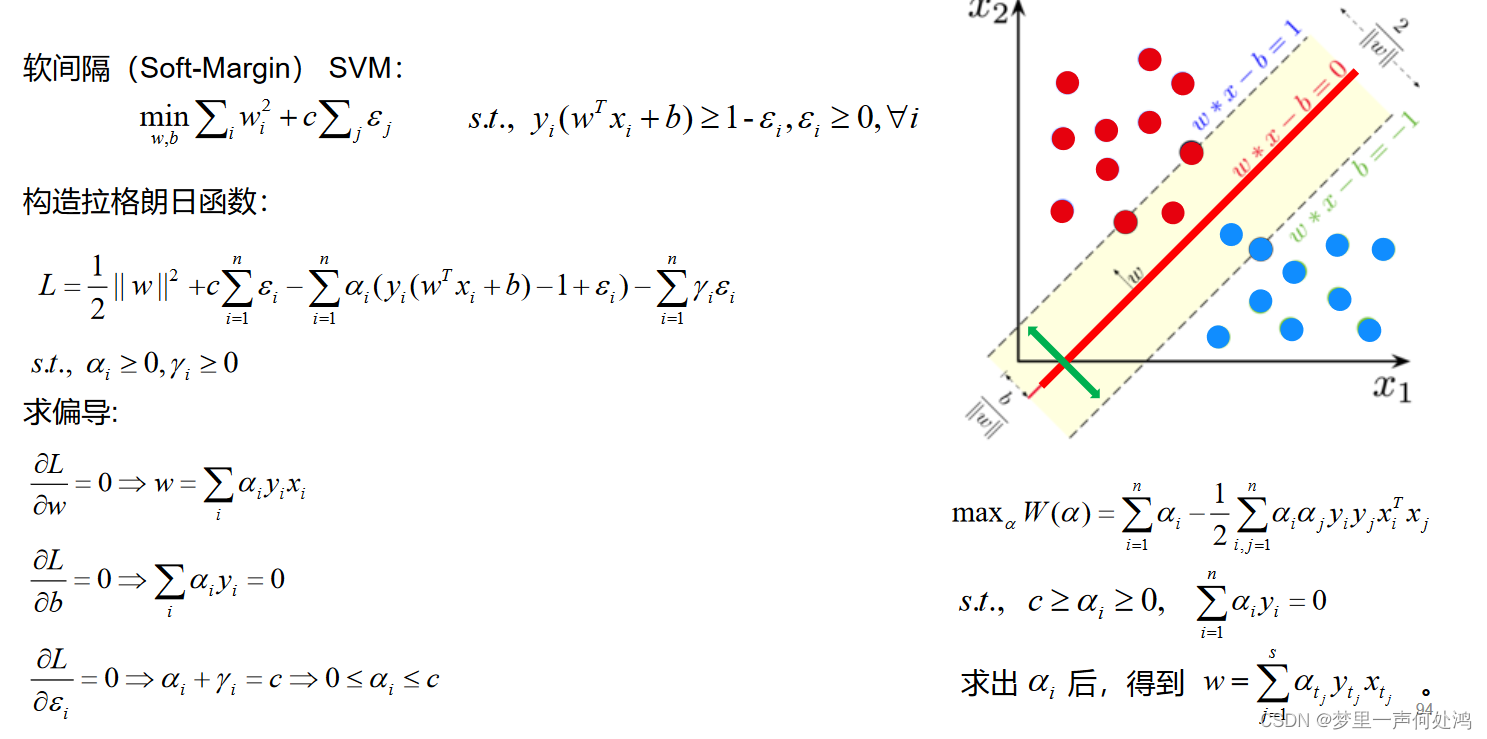
相关文章:

模式识别 —— 第六章 支持向量机(SVM)与核(Kernel)
模式识别 —— 第六章 支持向量机(SVM)与核(Kernel) 文章目录模式识别 —— 第六章 支持向量机(SVM)与核(Kernel)硬间隔(Hard-Margin)软间隔(Soft…...

总结 synchronized
目录synchronized的特性1. 互斥2. 刷新内存3. 可重入synchronized的使用1. 直接修饰普通方法2. 修饰静态方法3. 修饰代码块synchronized的锁机制基本特点关键锁策略 : 锁升级synchronized的特性 1. 互斥 synchronized 会起到互斥效果, 某个线程执行到某个对象的 synchronized…...

360周鸿祎又“开炮”:GPT 6-8就将产生自主意识!我们来测算一下对错
数据智能产业创新服务媒体——聚焦数智 改变商业近日,360的周鸿祎放言“GPT6到GPT8人工智能将会产生意识,变成新的物种。未来,人工智能大语言模型有可能实现自我进化,自动更新系统和自我升级,或者指数级进化能力&am…...
python——飞机大战小游戏
目录 1、导入模块 2、窗口操作 3、事件操作 4、长按事件 5、添加游戏背景 6、添加英雄飞机 7、获取飞机的图片矩形 8、基本游戏窗口 9、添加游戏窗口图片 10、英雄飞机登场 11、英雄飞机装备子弹并发射 1、enemy_plane 2、game_main 3、game_map 4、game_score …...
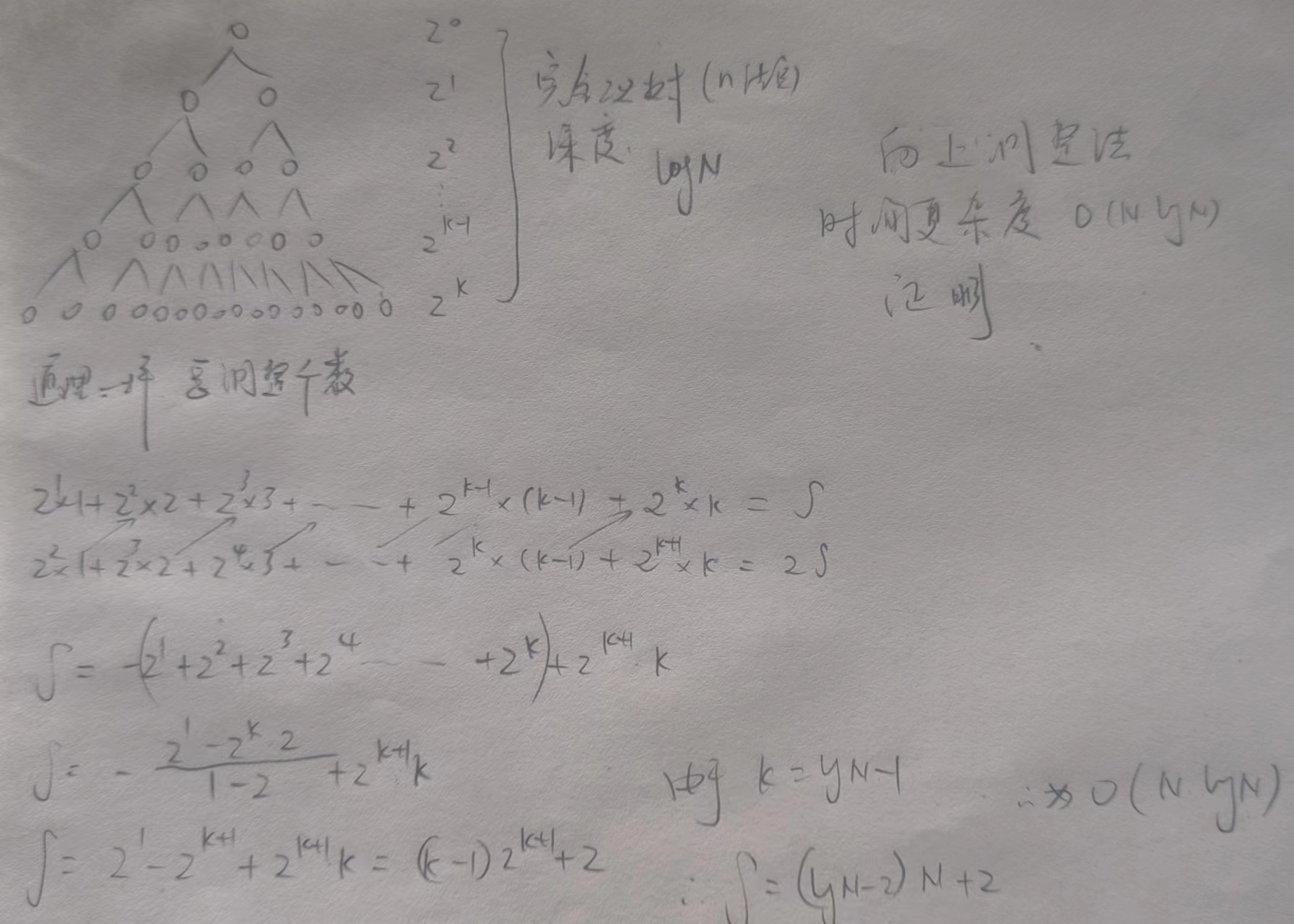
数组(完全二叉树)向下建堆法与堆排序O(N*logN)
TIPS AdjustUp & AdjustDown向上调整AdjustUp与向下调整AdjustDown的参数是一个数组(完全二叉树)需要进行调整操作的数值的下标/一个数组(完全二叉树)堆元素个数需要调整操作的数值的下标。实际上就是对完全二叉树当中的某一点…...

Lua require 函数使用
从 Lua 的用户文档中我们知道 require("modName") 函数是用来加载模块的,而如果这个modName已经用require 加载过的,再调用require时,将直接返回模块的值。因为函数首先查找 package.loaded 表, 检测 modName 是否被加载…...
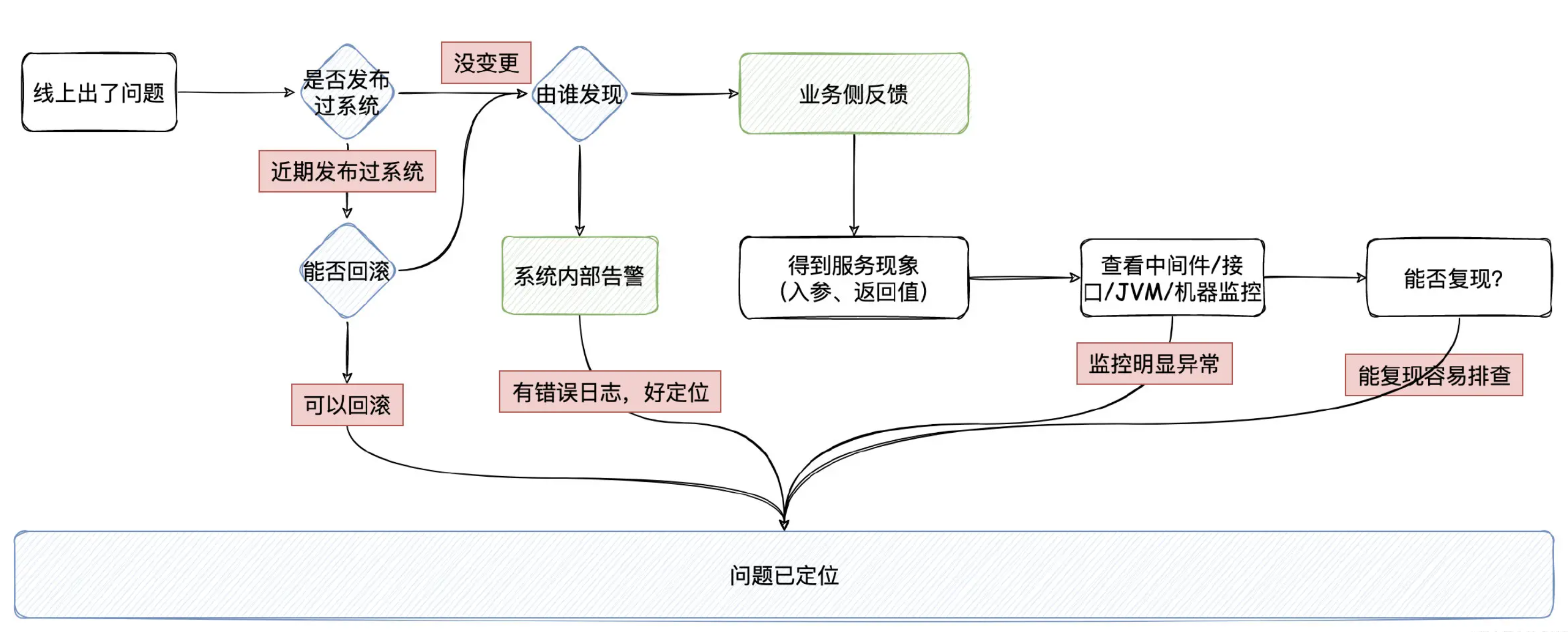
【面试】如何定位线上问题?
这个面试题我在两年社招的时候遇到过,前几天面试也遇到了。我觉得我每一次都答得中规中矩,今天来梳理复盘下,下次又被问到的时候希望可以答得更好。 下一次我应该会按照这个思路去答: 1、如果线上出现了问题,我们更多…...

字节二面,原来我对自动化测试的理解太浅了
如果你入职一家新的公司,领导让你开展自动化测试,作为一个新人,你肯定会手忙脚乱,你会如何落地自动化测试呢? 01 什么是自动化 有很多人做了很长时间的自动化但却连自动化的概念都不清楚,这样的人也是很悲…...

Android11.0 应用升级成功后立即断电重启,版本恢复
问题:客户反馈内置的应用升级成功后立刻断电重启,应用的版本被恢复。 使用adb命令升级客户应用,查看版本显示已更新,/data/system目录下packages.xml和packages.xml中应用版本信息均已更新 C:\Users\dell>adb shell dumpsys …...

关于python常用软件用法:Pycharm 常用功能
人生苦短,我用python 一.Pycharm的基本使用 1.在Pycharm下为你的Python项目配置Python解释器 (1).Setting>Project Interpreter>源码资料电子书:点击此处跳转文末名片获取 二.在Pycharm下创建Python文件、Python模块 1.File>New&g…...

SOLIDWORKS你不知道的小技巧
◉ SOLIDWORKS圆弧长度标注点智能标注,再选中该圆弧,然后分别点圆弧的两个端点,点击左键可以标注圆弧长度。◉ SOLIDWORKS强力裁剪剪裁实体中的强劲剪裁,除了可以裁剪实体外,还可以任意延伸实体。◉ SOLIDWORKS转折线转…...

有了HTTP,为啥还要用RPC
既然有 HTTP 请求,为什么还要用 RPC 调用? 一直以来都没有深究过RPC和HTTP的区别,不都是写一个服务然后在客户端调用么? HTTP和RPC最本质的区别,就是 RPC 主要是基于 TCP/IP 协议的,而 HTTP 服务主要是基…...

[leetcode] 动态规划
背包 先啃懂 背包九讲 01背包,即物品有限。 for 物品for 容量(倒序)P1048 [NOIP2005 普及组] 采药 [ 原题 | 题解 ] P1049 [NOIP2001 普及组] 装箱问题 [ 原题 | 题解 ] P1507 NASA的食物计划 [ 原题 | 题解 ] P1510 精卫填海 [ 原题 | 题…...
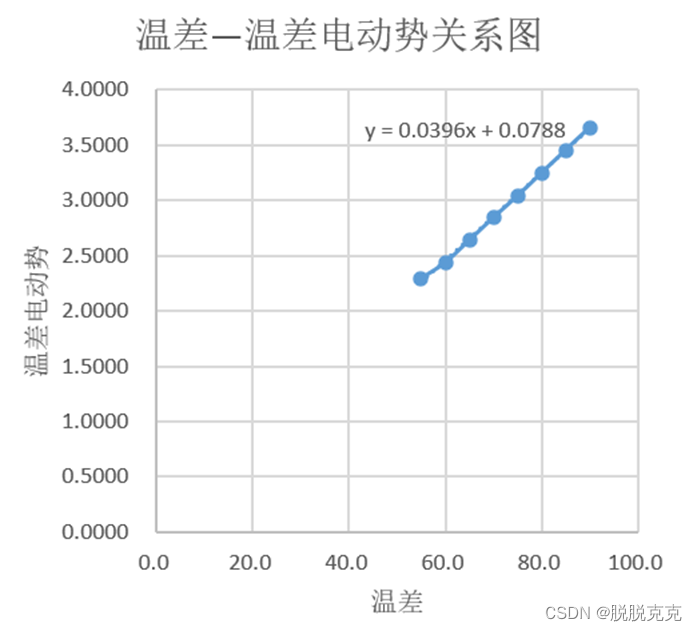
科大奥瑞物理实验——热电偶特性及其应用研究
实验名称:热电偶特性及其应用研究 1. 实验目的: 掌握电位差计的工作原理和结构特点;了解温差电偶测温的原理和方法;学会电位差计的使用及注意事项。 2. 实验器材: 电位差计 标准电池 光电检流计 稳压电源 温差电偶…...
)
Eclips快捷键大全(超详细)
Eclips快捷键大全(超详细)前言一、常用快捷键二、编辑快捷键三、导航快捷键四、运行和调试快捷键五、重构快捷键六、代码生成快捷键七、项目导航快捷键八、帮助快捷键九、搜索快捷键十、标记快捷键十一、版本控制快捷键十二、其它快捷键前言 本博主将用C…...
整懵了,蚂蚁金服4面成功拿下测开offer,涨薪10k,突然觉得跳槽也不是那么难
蚂蚁的面试挺独特的,每轮面试都没有HR约时间,一般是晚上8点左右面试官来一个电话,问是否能面试,能的话开始面,不能就约一个其他时间。 全程4面,前四面技术面,电话面试,最后一面是HR面…...

C++内存分布malloc-free-new-delete的区别和联系
目录 一、内存分布 1.1内存分布图: 1.2 为什么要将bss和data区分开呢? 1.3 堆和栈有什么区别 二、malloc、free;new、delete 2.1 new和delete是如何实现的,new与malloc的异同处 2.2既然有了malloc/free,C为什么还…...
)
【华为OD机试 2023最新 】 最多颜色的车辆(C++ 100%)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 在一个狭小的路口,每秒只能通过一辆车,假设车辆的颜色只有 3 种,找出 N 秒内经过的最多颜色的车辆数量。 三种颜色编号为0 ,1 ,2 输入描述 第一行输入的是通过的车辆颜色信息 [0,1,1,2] 代表4 秒钟通过的车…...

Linux安全加固
一、重要文件 /etc/passwd #记录本地用户的属性信息,如UID、GID /etc/shadow #存放用户的口令信息 只有系统管理员能查看 /etc/pam.d/system-auth #账户安全配置文件 /etc/login.defs #修改登录的配置文件 /etc/profile …...

Java基础学习(6)
Java基础学习一 字符串1.1 API 与 API文档1.1.1 如何使用帮助文档查找想要导用的方法1.2 String 概述1.3 创建String对象的两种方式第一种第二种1.4 Java常用字符串方法1.4.1 比较1.4.2 字符串通过索引取出1.4.3 取出字符串中的单个字符1.4.4 替换出字符串当中的字符1.4.5 取出…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
