【Python入门第四十二天】Python丨NumPy 数组裁切
裁切数组
python 中裁切的意思是将元素从一个给定的索引带到另一个给定的索引。
我们像这样传递切片而不是索引:[start:end]。
我们还可以定义步长,如下所示:[start:end:step]。
如果我们不传递 start,则将其视为 0。
如果我们不传递 end,则视为该维度内数组的长度。
如果我们不传递 step,则视为 1。
实例
从下面的数组中裁切索引 1 到索引 5 的元素:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[1:5])
运行实例

注释:结果包括了开始索引,但不包括结束索引。
实例
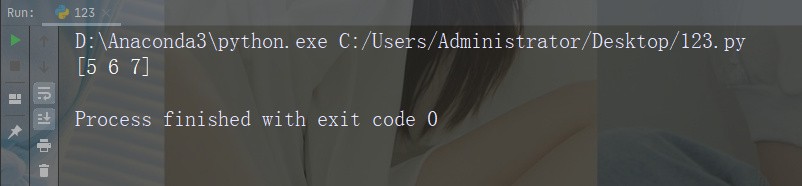
裁切数组中索引 4 到结尾的元素:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[4:])
运行实例
实例
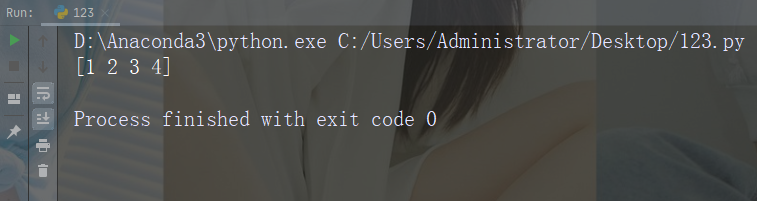
裁切从开头到索引 4(不包括)的元素:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[:4])
运行实例
负裁切
使用减号运算符从末尾开始引用索引:
实例
从末尾开始的索引 3 到末尾开始的索引 1,对数组进行裁切:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[-3:-1])
运行实例

STEP
请使用 step 值确定裁切的步长:
实例
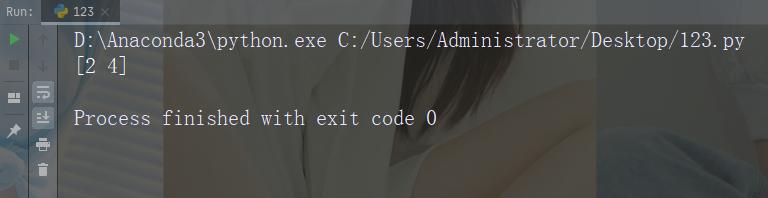
从索引 1 到索引 5,返回相隔的元素:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[1:5:2])
运行实例
实例
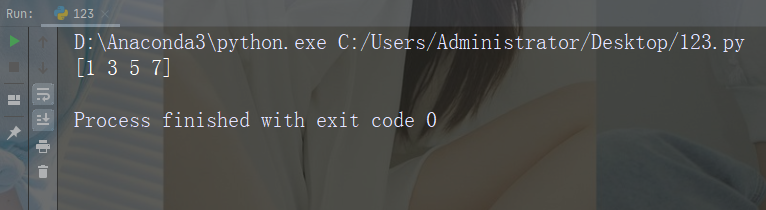
返回数组中相隔的元素:
import numpy as nparr = np.array([1, 2, 3, 4, 5, 6, 7])print(arr[::2])
运行实例
裁切 2-D 数组
实例
从第二个元素开始,对从索引 1 到索引 4(不包括)的元素进行切片:
import numpy as nparr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])print(arr[1, 1:4])
运行实例
注释:请记得第二个元素的索引为 1。
实例
从两个元素中返回索引 2:
import numpy as nparr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])print(arr[0:2, 2])
运行实例

实例
从两个元素裁切索引 1 到索引 4(不包括),这将返回一个 2-D 数组:
import numpy as nparr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])print(arr[0:2, 1:4])
运行实例
相关文章:

【Python入门第四十二天】Python丨NumPy 数组裁切
裁切数组 python 中裁切的意思是将元素从一个给定的索引带到另一个给定的索引。 我们像这样传递切片而不是索引:[start:end]。 我们还可以定义步长,如下所示:[start:end:step]。 如果我们不传递 start&…...
Anaconda配置Python新版本tensorflow库(CPU、GPU通用)的方法
本文介绍在Anaconda环境中,下载并配置Python中机器学习、深度学习常用的新版tensorflow库的方法。 在之前的两篇文章基于Python TensorFlow Estimator的深度学习回归与分类代码——DNNRegressor(https://blog.csdn.net/zhebushibiaoshifu/article/detail…...
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决报错信息原因查明网传解决措施好消息我的解决措施报错信息 查了下,在网上还是个比较常见的报错 一般为加载某模型时突然报错 原因查明 一般为下载某个 XXX_model.bin 的…...

sessionStorage , localStorage 和cookie的区别
一.sessionStorage(临时存储)sessionStorage是HTML5中新增的Web Storage API之一,用于在浏览器中存储键值对数据,与localStorage类似,但是sessionStorage存储的数据在会话结束时会被清除。可以通过以下方式使用sessionStorage:存储…...

C# 实例详解委托之Func、Action、delegate
委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,这个文章主要就这三种委托的用法通过实例展开讲解。 【Func】:Func是带返回值的委托: 原型函数如下(以下展示的…...
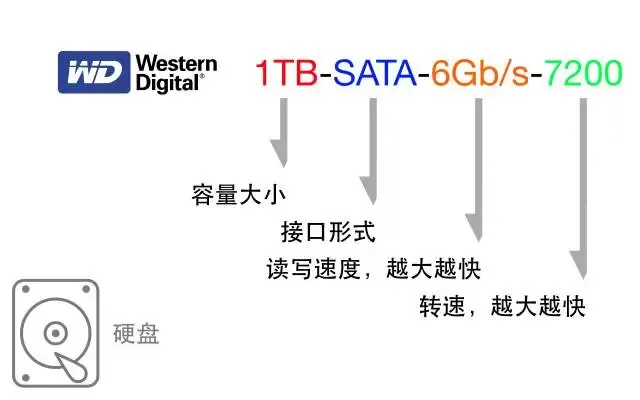
如何选电脑
1、CPU(中央处理器) 怎么看CPU型号:CPU:系列-代数等级核心显卡型号电压后缀 例如CPU:i7-10750H : 1、系列:Intel的酷睿i3、i5、i7、i9这四个系列的CPU,数字越大就代表越高端。 2、代数:代表…...

SpringBoot项目创建
如果使用spring的源地址创建项目失败,就使用 阿里云的springBoot项目创建地址:https://start.aliyun.com/ 1.new 一个新的项目: 2.选择合适的版本java的JDK和maven项目 3.选择spring web依赖 4.直接finish 5. 删除无用的包,然后…...

神经衰弱该如何判断?确诊为神经衰弱,日常要做好这7大护理!
神经衰弱是由于长时间处于紧张或者压力的情况下导致精神出现兴奋或者疲乏现象而伴随着一系列症状。如情绪烦恼、容易激怒、睡眠障碍、肌肉出现紧张性疼痛等,生活中有很多人在自己的不到休息或者遇到强大打击时就会嘲笑自己患上神经衰弱。甚至一些会盲目采取措施&…...

Linux之进程替换
进程替换1.什么是进程替换2.替换函数2.1 execl函数2.2 execv函数2.3 execlp函数2.4 execvp函数2.5 在自己的C程序上如何运行其他语言的程序?2.6 execle 函数2.7 小结3.一个简易的shell1.什么是进程替换 fork()之后,父子各自执行父进程代码的一部分&…...

关于清除浮动
浮动最早是用来做图文排版,为了让块级元素同行显示,而html中块元素是有自己的排列规则,一般独占一行。所以有了浮动元素,一旦元素浮动了就会脱离文档流,产生问题。怎么去清除浮动:(1)…...

Uber H3 index 地图索引思考
H3 是 uber 设计的六边形空间索引,go 语言操作包是 h3-go,可以通过经纬度获取所在的 h3 六边形边界,每个经纬度对应的六边形都是确定的,每个六边形唯一对应了一个 h3index。在业务开发中,我们可以通过 h3index 来对地理…...

多线程的几种状态
Java-多线程的几种状态🔎1.NEW( 系统中线程还未创建,只是有个Thread对象)🔎2.RUNNABLE( (就绪状态. 又可以分成正在工作中和即将开始工作)🔎3.TERMINATED(系统中的线程已经执行完了,Thread对象还在)🔎4.TIMED_WAITING(指定时间等待…...

【算法题】1574. 删除最短的子数组使剩余数组有序
题目: 给你一个整数数组 arr ,请你删除一个子数组(可以为空),使得 arr 中剩下的元素是 非递减 的。 一个子数组指的是原数组中连续的一个子序列。 请你返回满足题目要求的最短子数组的长度。 示例 1: …...

理解对数——金融问题中的自然对数(以e为底的对数)
第3章 金融问题(Financial Matters)——金融问题中的自然对数If thou lend moneyto any ofMy people. ...thou shalt not beto him as a creditor;neither shall yelay upon him interest.(如果你借钱给我的任何人。 ……你不应该是他的债权人;也不可向他加息。)——…...

vue2进阶学习之路
HTML、CSS和JavaScript基础 在学习Vue2之前,需要掌握HTML、CSS和JavaScript的基础知识。包括HTML的标签、CSS的布局和样式、JavaScript的变量类型、条件语句、循环语句等。 Vue2的基础知识 掌握Vue2的基本概念和语法,包括Vue2实例、数据绑定、指令、组件…...

决策树ID3算法
1. 决策树ID3算法的信息论基础 机器学习算法其实很古老,作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过,有这么多条件,用哪个条件特征先做if,哪个条件特征后做if比较优呢&#…...

C++模板基础(一)
函数模板(一) ● 使用 template 关键字引入模板: template void fun(T) {…} – 函数模板的声明与定义 – typename 关键字可以替换为 class ,含义相同 – 函数模板中包含了两对参数:函数形参 / 实参;模板形…...
)
生产者消费者模型线程池(纯代码)
目录 生产者消费者模型 条件变量&&互斥锁(阻塞队列) makefile Task.hpp BlockQueue.hpp BlockQueueTest.cc 信号量&&互斥锁(环形队列) makefile RingQueue.hpp RingQueueTest.cc 线程池(封…...

K8s 应用的网络可观测性: Cilium VS DeepFlow
随着分布式服务架构的流行,特别是微服务等设计理念在现代应用普及开来,应用中的服务变得越来越分散,因此服务之间的通信变得越来越依赖网络,很有必要来谈谈实现微服务可观测性中越来越重要的一环——云原生网络的可观测。K8s 是微服务设计理念能落地的最重要的承载体,本文…...
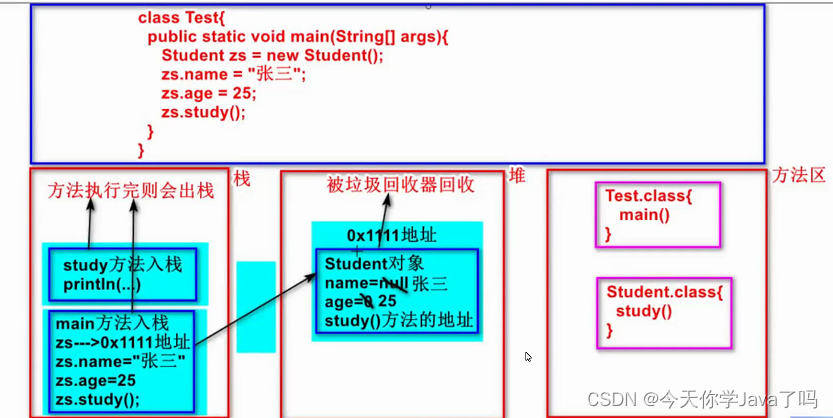
3.29面试题
文章目录内存内存管理执行过程要点面试题内存 内存管理 由JVM管理 堆:new出来的对象(包括成员变量、数组元素、方法的地址)栈:局部变量(包括方法的参数)方法区:.class字节码文件(…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
