P2847 [USACO16DEC] Moocast G
P2847 [USACO16DEC] Moocast G
[USACO16DEC] Moocast G
题面翻译
Farmer John 的 N N N 头牛 ( 1 ≤ N ≤ 1000 1 \leq N \leq 1000 1≤N≤1000) 为了在他们之间传播信息,想要组织一个"哞哞广播"系统。奶牛们决定去用步话机装备自己而不是在很远的距离之外互相哞哞叫,所以每一头奶牛都必须有一个步话机。这些步话机都有一个限制传播半径,但是奶牛们可以间接地通过中间奶牛传播信息,所以并不是每头牛都必须直接向其他每一头奶牛连边。
奶牛们需要去决定多少钱花在步话机上,如果他们花了 X X X, 那么他们都将会得到 X \sqrt{X} X 距离的步话机。所以,两头牛之间的欧几里得距离平方最多是 X X X。请帮助奶牛们找到最小的 X X X 使得图是强连通的。
题目描述
Farmer John’s N N N cows ( 1 ≤ N ≤ 1000 1 \leq N \leq 1000 1≤N≤1000) want to organize an emergency “moo-cast” system for broadcasting important messages among themselves.
Instead of mooing at each-other over long distances, the cows decide to equip themselves with walkie-talkies, one for each cow. These walkie-talkies each have a limited transmission radius, but cows can relay messages to one-another along a path consisting of several hops, so it is not necessary for every cow to be able to transmit directly to every other cow.
The cows need to decide how much money to spend on their walkie-talkies. If they spend X X X, they will each get a walkie-talkie capable of transmitting up to a distance of X \sqrt{X} X. That is, the squared distance between two cows must be at most X X X for them to be able to communicate.
Please help the cows determine the minimum integer value of X X X such that a broadcast from any cow will ultimately be able to reach every other cow.
输入格式
The first line of input contains N N N.
The next N N N lines each contain the x x x and y y y coordinates of a single cow. These are both integers in the range 0 … 25 , 000 0 \ldots 25,000 0…25,000.
输出格式
Write a single line of output containing the integer X X X giving the minimum amount the cows must spend on walkie-talkies.
样例 #1
样例输入 #1
4
1 3
5 4
7 2
6 1
样例输出 #1
17
提示
没有提示
题解
根本用不着二分答案嘛。直接 N 2 N^2 N2建边,跑一遍Kruskal。记录在最小生成树中的最长的一条边。显然只要使得这条边能够建立,那么这棵最小生成树中的所有的边都可以建立。答案就是最长的边的距离的平方,注意要用 d o u b l e double double存边权。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int maxn = 1e3+3;
int n, x[maxn], y[maxn], cnt, tot, f[maxn];
double Ans;
struct Edge{int u, v;double w;
}ed[maxn * maxn];
inline bool cmp(Edge a, Edge b){return a.w < b.w;
}
inline int find(int x){if(x == f[x]) return x;else return f[x] = find(f[x]);
}
inline void Kruskal(){for(int i=1; i<=n; i++) f[i] = i;for(int i=1; i<=n; i++){for(int j=1; j<=n; j++){if(i != j){++cnt;ed[cnt].u = i, ed[cnt].v = j, ed[cnt].w = sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));}}}sort(ed+1, ed+1+cnt, cmp);for(int i=1; i<=cnt; i++){int xx = find(ed[i].u), yy = find(ed[i].v);if(xx != yy){f[xx] = find(yy);tot ++;Ans = ed[i].w;}if(tot == n-1){break;}}
}int main(int argc, const char * argv[]){scanf("%d", &n);for(int i=1; i<=n; i++){scanf("%d%d", &x[i], &y[i]);}Kruskal();printf("%.0lf", Ans * Ans);
}
//Written by Kevin ☑
当然,最小生成树才是这道题的最优解
为什么呢?大家应该都学过勾股定理吧?在平面直角坐标系中,两点A(x1,y1),B(x2,y2)的距离|AB|等于 s q r t ( ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 sqrt((x1-x2)^2+(y1-y2)^2 sqrt((x1−x2)2+(y1−y2)2,而我们可以发现,我们最后要求的是最大的 ∣ A B ∣ 2 |AB|^2 ∣AB∣2,也就是 ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 (x1-x2)^2+(y1-y2)^2 (x1−x2)2+(y1−y2)2(当然在C++里得写成(x1-x2) * (x1-x2)+(y1-y2) * (y1-y2)),所以,我们只要求出边权为两点距离平方的最小生成树中最长边的长就可以了。
首先,我们可以通过一次双重循环求出每条边的边权,然后再跑一边最小生成树算法。
被熟知的求最小生成树的算法有prime、kruskal两种,而这次我们的图是完全图(即图的每两点之间都有连边),而prime更适合跑稠密图,因此我们选用prime算法。
#include<bits/stdc++.h>
using namespace std;
long long n,i,j,x[1001],y[1001],p[1001][1001],d[1001],u,max1;
bool b[1001];
priority_queue<pair<long long,long long> >q;//堆优化
int main(int argc, const char * argv[]){scanf("%lld",&n);for (i=1;i<=n;i++)scanf("%lld%lld",&x[i],&y[i]);for (i=1;i<=n;i++)for (j=1;j<=n;j++)p[i][j]=(x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);//求出两两点之间的距离for (i=1;i<=n;i++) d[i]=1e11;d[1]=0;max1=0;q.push(make_pair(0,1));while (q.size()){u=q.top().second;q.pop();if (b[u]) continue;max1=max(max1,d[u]);//求出最大边权b[u]=true;for (i=1;i<=n;i++)if (d[i]>p[u][i]){d[i]=p[u][i];q.push(make_pair(-d[i],i));//prime}}printf("%lld",max1);return 0;
}
//Written by Kevin ☑︎
相关文章:

P2847 [USACO16DEC] Moocast G
P2847 [USACO16DEC] Moocast G [USACO16DEC] Moocast G 题面翻译 Farmer John 的 N N N 头牛 ( 1 ≤ N ≤ 1000 1 \leq N \leq 1000 1≤N≤1000) 为了在他们之间传播信息,想要组织一个"哞哞广播"系统。奶牛们决定去用步话机装备自己而不是在很远的距离…...

针对国内AIGC市场,国内目前出台了那些法律法规?
针对国内AIGC市场,特别是AI生成与合成内容方面,中国已经出台了一系列法律法规来规范其发展和应用。 图片源自“央视新闻” 以下是一些主要的法律法规: 一、国家层面的法律法规 《中华人民共和国网络安全法》 施行时间:2017年6月…...

Windows+Ubuntu双系统下时钟设置
Ubuntu默认把系统时间(硬件时钟)设置为UTC时间,并根据本地时区和夏令时设置自动调整本地时间,这是一种很合理很优雅的处理硬件时钟和本地时钟的模式。而Windows系统是默认情况下把系统时间设置为本地时间,历来独霸电脑…...

一些写leetcode的笔记
标准库中的string类没有实现像C#和Java中string类的split函数,所以想要分割字符串的时候需要我们自己手动实现。但是有了stringstream类就可以很容易的实现,stringstream默认遇到空格、tab、回车换行会停止字节流输出。 #include <sstream> #incl…...

shopify主题开发之template模板解析
在 Shopify 主题开发中,template 文件是核心部分,它们定义了店铺中不同页面的布局和结构。下面将详细介绍 Shopify 主题中的 template 模板。 一、template 文件结构 在 Shopify 主题中,templates 文件夹包含了所有用于生成店铺页面的模板文…...

Zookeeper学习
文章目录 学习第 1 章 Zookeeper 入门1.1 概述Zookeeper工作机制 1.2 特点1.3 数据结构1.4 应用场景统一命名服务统一配置管理统一集群管理服务器动态上下线软负载均衡 1.5 下载zookeeper 第 2 章 Zookeeper 本地安装2.1 本地模式安装安装前准备配置修改操作 Zookeeper本地安装…...
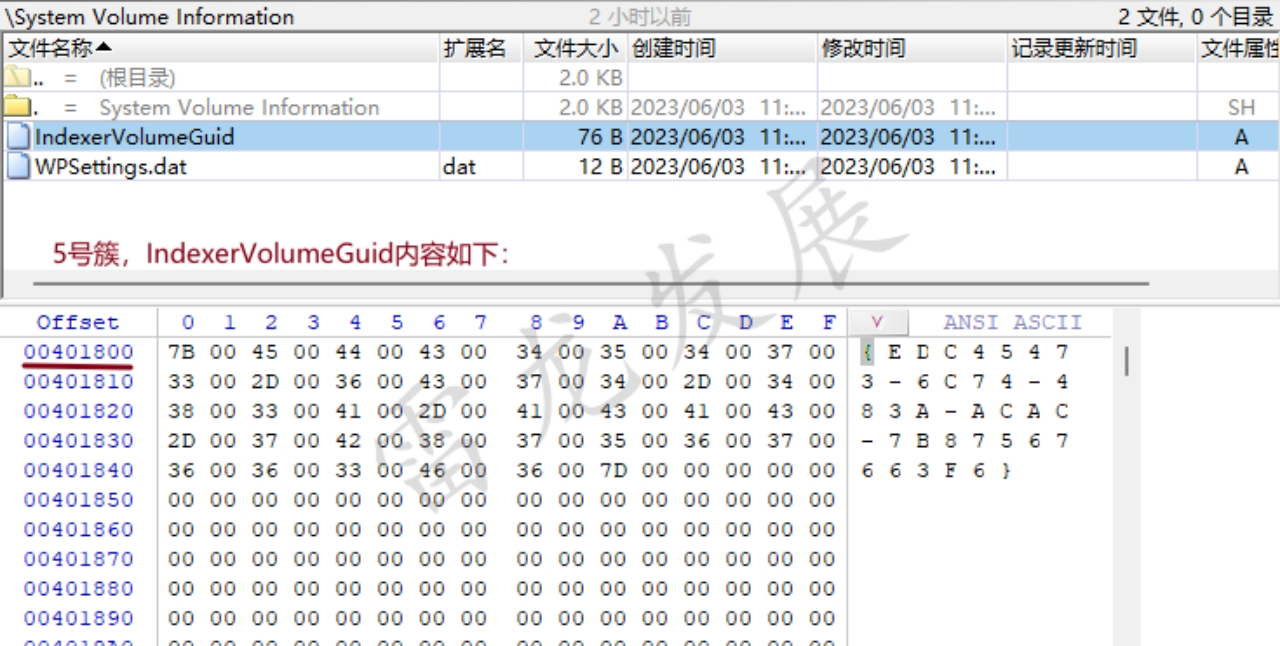
FAT32文件系统详细分析 (格式化SD nandSD卡)
FAT32 文件系统详细分析 (格式化 SD nand/SD 卡) 目录 FAT32 文件系统详细分析 (格式化 SD nand/SD 卡)1. 前言2.格式化 SD nand/SD 卡3.FAT32 文件系统分析3.1 保留区分析3.1.1 BPB(BIOS Parameter Block) 及 BS 区分析3.1.2 FSInfo 结构扇区分析3.1.3 引导扇区剩余扇区3.1.4 …...

通义灵码在Visual Studio上
通义灵码在Visual Studio上不好用,有时候会出现重影,不如原生的自动补全好用,原生的毕竟的根据语法来给出提示的。...
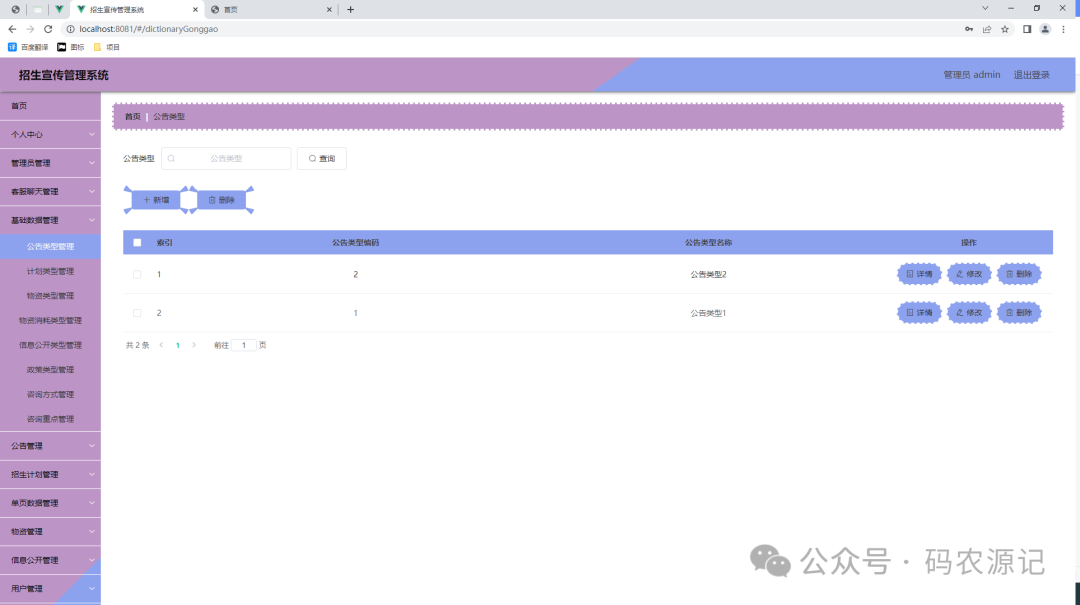
基于SpringBoot的招生宣传管理系统【附源码】
基于SpringBoot的招生宣传管理系统(源码L文说明文档) 目录 4 系统设计 4.1 系统概述 4.2系统功能结构设计 4.3数据库设计 4.3.1数据库E-R图设计 4.3.2 数据库表结构设计 5 系统实现 5.1管理员功能介绍 5.1.1管理员登录 …...

SOT23封装1A电流LDO具有使能功能的 1A、低 IQ、高精度、低压降稳压器系列TLV757P
前言 SOT23-5封装的外形和丝印 该LDO适合PCB空间较小的场合使用,多数SOT23封装的 LDO输出电流不超过0.5A。建议使用时输入串联二极管1N4001,PCB布局需要考虑散热,参考文末PCB布局。 1 特性 • 采用 SOT-23 (DYD) 封装,具有 60.3C/W RθJA •…...

python绘制3d建筑
import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d.art3d import Poly3DCollection# 随机生成建筑块数据 def generate_building_blocks(num_blocks, grid_size100, height_range(5, 50), base_size_range(10, 30)):buildings []for _ in range(…...

机器学习实战21-基于XGBoost算法实现糖尿病数据集的分类预测模型及应用
大家好,我是微学AI,今天给大家介绍一下机器学习实战21-基于XGBoost算法实现糖尿病数据集的分类预测模型及应用。首先阐述了 XGBoost 算法的数学原理及公式,为模型构建提供理论基础。接着利用 kaggle 平台的糖尿病数据集,通过详细的…...

ElasticSearch数据类型和分词器
一、数据类型 1、Text (文本数据类型) 2、Keyword(关键字数据类型) 3、Alias(别名类型) 4、Arrays (集合类型) 5、Boolean(布尔类型) 6、日期类型 7、Numeric (数…...

【云原生监控】Prometheus之PushGateway
Prometheus之PushGateway 文章目录 Prometheus之PushGateway介绍作用资源列表基础环境一、部署PushGateway1.1、下载软件包1.2、解压软件包1.3、编辑配置systemctl启动文件1.4、创建日志目录1.5、加载并启动1.6、监控端口1.7、访问PushGateway 二、 配置Prometheus抓取PushGate…...

sqlalchemy JSON 字段写入时中文序列化问题
JSON字段定义 from sqlalchemy import Column, JSONclass Table(Base):__tablename__ "table"__table_args__ ({"comment": "表名称"})...extra Column(JSON, comment"其他属性")...局部序列化 def create(extra):table Table()#…...
C++ 类域+类的对象大小
个人主页:Jason_from_China-CSDN博客 所属栏目:C系统性学习_Jason_from_China的博客-CSDN博客 所属栏目:C知识点的补充_Jason_from_China的博客-CSDN博客 概念概述 类定义了一个新的作用域,类的所有成员都在类的作用域中ÿ…...

QT开发:深入详解QtCore模块事件处理,一文学懂QT 事件循环与处理机制
Qt 是一个跨平台的 C 应用程序框架,QtCore 模块提供了核心的非 GUI 功能。事件处理是 Qt 应用程序的重要组成部分。Qt 的事件处理机制包括事件循环和事件处理,它们共同确保应用程序能够响应用户输入、定时器事件和其他事件。 1. 事件循环(Ev…...
小米,B站网络安全岗位笔试题目+答案
《网安面试指南》http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247484339&idx1&sn356300f169de74e7a778b04bfbbbd0ab&chksmc0e47aeff793f3f9a5f7abcfa57695e8944e52bca2de2c7a3eb1aecb3c1e6b9cb6abe509d51f&scene21#wechat_redirect 《Java代码审…...

微信小程序中巧妙使用 wx:if 和 catchtouchmove 实现弹窗禁止页面滑动功能
大家好,今天我要和大家分享的是在微信小程序开发过程中,如何利用 wx:if 或 wx:elif 来条件性地渲染不同的元素,并结合 catchtouchmove 事件处理函数来解决弹窗弹出时禁止背后页面滑动,而弹窗消失时恢复滑动的功能。 在微信小程序…...

唯徳知识产权管理系统 DownloadFileWordTemplate 文件读取漏洞复现
0x01 产品简介 唯徳知识产权管理系统,由深圳市唯德科创信息有限公司精心打造,旨在为企业及代理机构提供全方位、高效、安全的知识产权管理解决方案。该系统集成了专利、商标、版权等知识产权的全面管理功能,并通过云平台实现远程在线办公,提升工作效率。是一款集知识产权申…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
