深度学习中的损失函数
文章目录
- 一. Loss函数
- 1. 均方差损失(Mean Squared Error Loss)
- 2. 平均绝对误差损失(Mean Absolute Error Loss)
- 3.(Huber Loss)
- 4. 分位数损失(Quantile Loss)
- 5. 交叉熵损失(Cross Entropy Loss)
- 5.1 二分类:
- 5.2 多分类:
- 5.3 Logistics loss和Cross Entropy Loss:
- 5.4. 为什么用交叉熵损失:
- 6. 合页损失(Hinge Loss)
- 7. 0/1损失函数
- 8. 指数损失
- 9. 对数损失/对数似然损失(Log-likelihood Loss)
- 10. Smooth L1 Loss
一. Loss函数
机器学习中的监督学习本质上是给定一系列训练样本(xi,yi)(x_i,y_i)(xi,yi),尝试学习x−yx-yx−y的映射关系,使得给定一个xxx,即便这个xxx不在训练样本中,也能够输出y^\hat{y}y^,尽量与真实的yyy接近。损失函数是用来估量模型的输出y^\hat{y}y^与真实值yyy之间的差距,给模型的优化指引方向。模型的结构风险包括了经验风险和结构风险,损失函数是经验风险函数的核心部分:
θ^=argminθ1N∑i=1NL(yi,f(xi;θ)+λΦ(θ))\hat{\theta}=\arg \min _{\theta} \frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i} ; \theta\right)+\lambda \Phi(\theta)\right) θ^=argθminN1i=1∑NL(yi,f(xi;θ)+λΦ(θ))
式中,前面的均值函数为经验风险,L(yi,f(xi;θ))L\left(y_{i},f\left(x_{i};\theta\right)\right)L(yi,f(xi;θ))为损失函数,后面的项为结构风险,Φ(θ)\Phi(\theta)Φ(θ)衡量模型的复杂度.
首先区分损失函数、代价函数和目标函数之间的区别和联系:
- 损失函数(Loss Function)通常是针对单个训练样本而言,给定一个模型输出y^\hat{y}y^和一个真实值yyy,损失函数输出一个实值损失L=f(yi,y^)L=f(y_i,\hat{y})L=f(yi,y^),比如说:
- 线性回归中的均方差损失:L(yi,f(xi;θ)=(f(xi;θ)−yi)2L\left(y_{i}, f\left(x_{i} ; \theta\right)=\left(f\left(x_{i} ; \theta\right)-y_{i}\right)^{2}\right.L(yi,f(xi;θ)=(f(xi;θ)−yi)2
- SVM中的Hinge损失:L(yi,f(xi;θ)=max(0,1−f(xi;θ)yi)L\left(y_{i}, f\left(x_{i} ; \theta\right)=\max \left(0,1-f\left(x_{i} ; \theta\right) y_{i}\right)\right.L(yi,f(xi;θ)=max(0,1−f(xi;θ)yi)
- 精确度定义中的0/1损失:L(yi,f(xi;θ)=1)⟺f(xi;θ)≠yiL\left(y_{i}, f\left(x_{i} ; \theta\right)=1\right) \Longleftrightarrow f\left(x_{i} ; \theta\right) \neq y_{i}L(yi,f(xi;θ)=1)⟺f(xi;θ)=yi
- 代价函数(Cost Function)通常是针对整个训练集(或者在使用mini-batch gradient descent时的一个mini-batch)的总损失J=∑i=1Nf(yi,y^i)J=\sum_{i=1}^{N} f\left(y_{i}, \hat{y}_{i}\right)J=∑i=1Nf(yi,y^i),比如说:
- 均方误差:MSE(θ)=1N∑i=1N(f(xi;θ)−yi)2M S E(\theta)=\frac{1}{N} \sum_{i=1}^{N}\left(f\left(x_{i} ; \theta\right)-y_{i}\right)^{2}MSE(θ)=N1∑i=1N(f(xi;θ)−yi)2
- SVM的代价函数:SVM(θ)=∥θ∥2+C∑i=1NξiS V M(\theta)=\|\theta\|^{2}+C \sum_{i=1}^{N} \xi_{i}SVM(θ)=∥θ∥2+C∑i=1Nξi
- 目标函数(Objective Function)通常是一个更通用的术语,表示任意希望被优化的函数,用于机器学习领域和非机器学习领域(比如运筹优化),比如说,最大似然估计(MLE)中的似然函数就是目标函数
一句话总结三者的关系就是:A loss function is a part of a cost function which is a type of an objective function
1. 均方差损失(Mean Squared Error Loss)
均方差(Mean Squared Error,MSE)损失是机器学习、深度学习回归任务中最常用的一种损失函数,也称为 L2 Loss。其基本形式如下:
JMSE=1N∑i=1N(yi−y^i)2J_{M S E}=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} JMSE=N1i=1∑N(yi−y^i)2
背后的假设:
实际上在一定的假设下,我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布(μ=0,σ=1)(\mu=0, \sigma=1)(μ=0,σ=1),则给定一个xix_ixi,模型就输出真实值yiy_iyi的概率为:
p(yi∣xi)=12πexp(−(yi−y^i)22)p\left(y_{i} \mid x_{i}\right)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\left(y_{i}-\hat{y}_{i}\right)^{2}}{2}\right) p(yi∣xi)=2π1exp(−2(yi−y^i)2)
进一步我们假设数据集中N个样本点之间相互独立,则给定所有xxx输出所有真实值yyy的概率,即似然(Likelihood)为所有p(yi∣xi)p\left(y_{i} \mid x_{i}\right)p(yi∣xi)的累乘:
L(x,y)=∏i=1N12πexp(−(yi−y^i)22)L(x, y)=\prod_{i=1}^{N} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\left(y_{i}-\hat{y}_{i}\right)^{2}}{2}\right) L(x,y)=i=1∏N2π1exp(−2(yi−y^i)2)
通常为了计算方便,我们通常最大化对数似然(Log-Likelihood):
LL(x,y)=log(L(x,y))=−N2log2π−12∑i=1N(yi−y^i)2LL(x, y)=\log (L(x, y))=-\frac{N}{2} \log 2 \pi-\frac{1}{2} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} LL(x,y)=log(L(x,y))=−2Nlog2π−21i=1∑N(yi−y^i)2
去掉与y^i\hat{y}_{i}y^i无关的第一项,然后转化为最小化负对数似然(Negative Log-Likelihood):
NLL(x,y)=12∑i=1N(yi−y^i)2N L L(x, y)=\frac{1}{2} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} NLL(x,y)=21i=1∑N(yi−y^i)2
可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下,最小化均方差损失函数与极大似然估计本质上是一致的,因此在这个假设能被满足的场景中(比如回归),均方差损失是一个很好的损失函数选择;当这个假设没能被满足的场景中(比如分类),均方差损失不是一个好的选择.
2. 平均绝对误差损失(Mean Absolute Error Loss)
平均绝对误差(Mean Absolute Error Loss,MAE)是另一类常用的损失函数,也称为L1 Loss。其基本形式如下:
JMAE=1N∑i=1N∣yi−y^i∣J_{M A E}=\frac{1}{N} \sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| JMAE=N1i=1∑N∣yi−y^i∣
背后的假设:
同样的我们可以在一定的假设下通过最大化似然得到 MAE 损失的形式,假设模型预测与真实值之间的误差服从拉普拉斯分布 Laplace distribution(μ=0,b=1)(\mu=0, b=1)(μ=0,b=1),则给定一个xix_ixi模型输出真实值yiy_iyi的概率为:
p(yi∣xi)=12exp(−∣yi−y^i∣)p\left(y_{i} \mid x_{i}\right)=\frac{1}{2} \exp \left(-\left|y_{i}-\hat{y}_{i}\right|\right) p(yi∣xi)=21exp(−∣yi−y^i∣)
与上面推导 MSE 时类似,我们可以得到的负对数似然(Negative Log-Likelihood)实际上就是MAE 损失的形式:
L(x,y)=∏i=1N12exp(−∣yi−y^i∣)L(x, y)=\prod_{i=1}^{N} \frac{1}{2} \exp \left(-\left|y_{i}-\hat{y}_{i}\right|\right) L(x,y)=i=1∏N21exp(−∣yi−y^i∣)
LL(x,y)=−N2−∑i=1N∣yi−y^i∣L L(x, y)=-\frac{N}{2}-\sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| LL(x,y)=−2N−i=1∑N∣yi−y^i∣
$$
N L L(x, y)=\sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right|
$$
MAE与MSE的区别:
- MSE比MAE能够更快收敛:当使用梯度下降算法时,MSE损失的梯度为−y^i-\hat{y}_{i}−y^i,而MAE损失的梯度为±1\pm 1±1。所以。MSE的梯度会随着误差大小发生变化,而MAE的梯度一直保持为1,这不利于模型的训练
- MAE对异常点更加鲁棒:从损失函数上看,MSE对误差平方化,使得异常点的误差过大;从两个损失函数的假设上看,MSE假设了误差服从高斯分布,MAE假设了误差服从拉普拉斯分布,拉普拉斯分布本身对于异常点更加鲁棒

3.(Huber Loss)
Huber Loss是一种将MSE与MAE结合起来,取两者优点的损失函数,也被称作Smooth Mean Absolute Error Loss。其原理很简单,就是在误差接近0时使用MSE,误差较大时使用MAE,公式为:
Jhuber =1N∑i=1NI∣yi−y^i∣≤δ(yi−y^i)22+I∣yi−y^i∣>δ(δ∣yi−y^i∣−12δ2)J_{\text {huber }}=\frac{1}{N} \sum_{i=1}^{N} \mathbb{I}_{\left|y_{i}-\hat{y}_{i}\right| \leq \delta} \frac{\left(y_{i}-\hat{y}_{i}\right)^{2}}{2}+\mathbb{I}_{\left|y_{i}-\hat{y}_{i}\right|>\delta}\left(\delta\left|y_{i}-\hat{y}_{i}\right|-\frac{1}{2} \delta^{2}\right) Jhuber =N1i=1∑NI∣yi−y^i∣≤δ2(yi−y^i)2+I∣yi−y^i∣>δ(δ∣yi−y^i∣−21δ2)
上式中,δ\deltaδ是Huber Loss的一个超参数,δ\deltaδ的值是MSE与MAE两个损失连接的位置。下图为δ=1.0\delta=1.0δ=1.0时的Huber Loss:

可以看到在[−δ,δ][-\delta, \delta][−δ,δ]内实际上就是MSE的损失,使损失函数可导并且梯度更加稳定;在(−∞,δ)(-\infty, \delta)(−∞,δ)和(δ,∞)(\delta, \infty)(δ,∞)区间内为MAE损失,降低了异常点的影响,使训练更加鲁棒.
4. 分位数损失(Quantile Loss)
分位数回归Quantile Regression是一类在实际应用中非常有用的回归算法,通常的回归算法是拟合目标值的期望(MSE)或者中位数(MAE),而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点,得到一个置信区间,如下图所示:

分位数回归是通过使用分位数损失Quantile Loss来实现这一点的,分位数损失形式如下:
Jquant =1N∑i=1NIy^i≥yi(1−r)∣yi−y^i∣+Iy^i<yir∣yi−y^i∣J_{\text {quant }}=\frac{1}{N} \sum_{i=1}^{N} \mathbb{I}_{\hat{y}_{i} \geq y_{i}}(1-r)\left|y_{i}-\hat{y}_{i}\right|+\mathbb{I}_{\hat{y}_{i}<y_{i}} r\left|y_{i}-\hat{y}_{i}\right| Jquant =N1i=1∑NIy^i≥yi(1−r)∣yi−y^i∣+Iy^i<yir∣yi−y^i∣
式中的r为分位数,这个损失函数是一个分段的函数,将y^i≥yi\hat{y}_{i} \geq y_{i}y^i≥yi(高估)和 y^i<yi\hat{y}_{i}<y_{i}y^i<yi (低估)时,低估的损失要比高估的损失更大;反之,当r<0.5r < 0.5r<0.5 时,高估的损失要比低估的损失更大,分位数损失实现了分别用不同的系数控制高估和低估的损失,进而实现分位数回归。特别地,当r=0.5r = 0.5r=0.5时,分位数损失退化为MAE损失,从这里可以看出 MAE 损失实际上是分位数损失的一个特例—中位数回归.
Jquant r=0.5=1N∑i=1N∣yi−y^i∣J_{\text {quant }}^{r=0.5}=\frac{1}{N} \sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| Jquant r=0.5=N1i=1∑N∣yi−y^i∣
5. 交叉熵损失(Cross Entropy Loss)
对于分类问题,最常用的损失函数是交叉熵损失函数(Cross Entropy Loss)
5.1 二分类:
考虑二分类,在二分类中我们通常使用Sigmoid函数将模型的输出压缩到(0,1)区间内,y^i∈(0,1)\hat{y}_{i} \in(0,1)y^i∈(0,1),用来代表给定输入xix_ixi,模型判断为正类的概率。由于只有正负两类,因此同时也得到了负类的概率:
p(yi=1∣xi)=y^ip\left(y_{i}=1 \mid x_{i}\right)=\hat{y}_{i} p(yi=1∣xi)=y^i
p(yi=0∣xi)=1−y^ip\left(y_{i}=0 \mid x_{i}\right)=1-\hat{y}_{i} p(yi=0∣xi)=1−y^i
将两条式子合并成一条:
p(yi∣xi)=(y^i)yi(1−y^i)1−yip\left(y_{i} \mid x_{i}\right)=\left(\hat{y}_{i}\right)^{y_{i}}\left(1-\hat{y}_{i}\right)^{1-y_{i}} p(yi∣xi)=(y^i)yi(1−y^i)1−yi
假设数据点之间独立同分布,则似然可以表示为:
L(x,y)=∏i=1N(y^i)yi(1−y^i)1−yiL(x, y)=\prod_{i=1}^{N}\left(\hat{y}_{i}\right)^{y_{i}}\left(1-\hat{y}_{i}\right)^{1-y_{i}} L(x,y)=i=1∏N(y^i)yi(1−y^i)1−yi
对似然取对数,然后加负号变成最小化负对数似然,即为交叉熵损失函数的形式:
NLL(x,y)=JCE=−∑i=1Nyilog(y^i)+(1−yi)log(1−y^i)N L L(x, y)=J_{C E}=-\sum_{i=1}^{N} y_{i} \log \left(\hat{y}_{i}\right)+\left(1-y_{i}\right) \log \left(1-\hat{y}_{i}\right) NLL(x,y)=JCE=−i=1∑Nyilog(y^i)+(1−yi)log(1−y^i)
下图是对二分类的交叉熵损失函数的可视化:

蓝线是目标值为0时输出不同输出的损失,黄线是目标值为1时的损失。可以看到约接近目标值损失越小,随着误差变差,损失呈指数增长.
5.2 多分类:
在多分类的任务中,交叉熵损失函数的推导思路和二分类是一样的,变化的地方是真实值[公式]是一个One-hot向量,同时模型输出的压缩由原来的Sigmoid函数换成Softmax函数。Softmax函数将每个维度的输出范围都限定在(0,1)之间,同时所有维度的输出和为1,用于表示一个概率分布
p(yi∣xi)=∏k=1K(y^ik)yikp\left(y_{i} \mid x_{i}\right)=\prod_{k=1}^{K}\left(\hat{y}_{i}^{k}\right)^{y_{i}^{k}} p(yi∣xi)=k=1∏K(y^ik)yik
其中,k∈Kk \in Kk∈K表示K个类别中的一类,同样的假设数据点之间独立同分布,可得到负对数似然为:
NLL(x,y)=JCE=−∑i=1N∑k=1Kyiklog(y^ik)N L L(x, y)=J_{C E}=-\sum_{i=1}^{N} \sum_{k=1}^{K} y_{i}^{k} \log \left(\hat{y}_{i}^{k}\right) NLL(x,y)=JCE=−i=1∑Nk=1∑Kyiklog(y^ik)
由于yiy_iyi是一个One-hot向量,除了目标类为1之外其他类别上的输出都为 0,因此上式也可以写为:
JCE=−∑i=1Nyicilog(yic^i)J_{C E}=-\sum_{i=1}^{N} y_{i}^{c_{i}} \log \left(y_{i}^{\hat{c}_{i}}\right) JCE=−i=1∑Nyicilog(yic^i)
其中,cic_ici是xix_ixi的目标类,通常这个应用于多分类的交叉熵损失函数也被称为Softmax Loss或者Categorical Cross Entropy Loss
5.3 Logistics loss和Cross Entropy Loss:
对于Logistics loss,我们说的是二分类问题,y^\hat{y}y^是一个数;对于Cross Entropy Loss,我们说的是多分类问题,y^\hat{y}y^是一个k维的向量。当k=2时,Logistics loss与Cross Entropy Loss一致.
5.4. 为什么用交叉熵损失:
分类中为什么不用均方差损失?上文在介绍均方差损失的时候讲到实际上均方差损失假设了误差服从高斯分布,在分类任务下这个假设没办法被满足,因此效果会很差。
为什么是交叉熵损失呢?
(1)一个角度是用最大似然来解释:也就是我们上面的推导
(2)另一个角度是用信息论来解释交叉熵损失:假设对于样本xix_ixi存在一个最优分布yi⋆y_{i}^{\star}yi⋆真实地表明了这个样本属于各个类别的概率,那么我们希望模型的输出y^i\hat{y}_{i}y^i尽可能地逼近这个最优分布,在信息论中,我们可以使用KL散度(Kullback–Leibler Divergence)来衡量两个分布的相似性。给定分布ppp和分布qqq, 两者的 KL 散度公式如下:
KL(p,q)=∑k=1Kplog(p)−∑k=1Kplog(q)K L(p, q)=\sum_{k=1}^{K} p \log (p)-\sum_{k=1}^{K} p \log (q) KL(p,q)=k=1∑Kplog(p)−k=1∑Kplog(q)
其中第一项为分布ppp的信息熵,第二项为分布ppp和分布qqq的交叉熵。将最优分布yi⋆y_{i}^{\star}yi⋆和输出分布y^i\hat{y}_{i}y^i代入分布ppp和分布qqq得到:
KL(yi⋆,y^i)=∑k=1Kyi⋆log(yi⋆)−∑k=1Kyi⋆log(y^i)K L\left(y_{i}^{\star}, \hat{y}_{i}\right)=\sum_{k=1}^{K} y_{i}^{\star} \log \left(y_{i}^{\star}\right)-\sum_{k=1}^{K} y_{i}^{\star} \log \left(\hat{y}_{i}\right) KL(yi⋆,y^i)=k=1∑Kyi⋆log(yi⋆)−k=1∑Kyi⋆log(y^i)
由于我们希望两个分布尽量相近,因此我们最小化KL散度。同时由于上式第一项信息熵仅与最优分布本身相关,因此我们在最小化的过程中可以忽略掉,变成最小化
∑k=1Kyi⋆log(y^i)\sum_{k=1}^{K} y_{i}^{\star} \log \left(\hat{y}_{i}\right) k=1∑Kyi⋆log(y^i)
我们并不知道最优分布yi⋆y_{i}^{\star}yi⋆,但训练数据里面的目标值yiy_iyi 可以看做是yi⋆y_{i}^{\star}yi⋆的一个近似分布:
−∑k=1Kyilog(y^i)-\sum_{k=1}^{K} y_{i} \log \left(\hat{y}_{i}\right) −k=1∑Kyilog(y^i)
这个是针对单个训练样本的损失函数,如果考虑整个数据集,则:
JKL=−∑i=1N∑k=1Kyiklog(y^ik)=−∑i=1Nyicilog(yic^i)J_{K L}=-\sum_{i=1}^{N} \sum_{k=1}^{K} y_{i}^{k} \log \left(\hat{y}_{i}^{k}\right)=-\sum_{i=1}^{N} y_{i}^{c_{i}} \log \left(y_{i}^{\hat{c}_{i}}\right) JKL=−i=1∑Nk=1∑Kyiklog(y^ik)=−i=1∑Nyicilog(yic^i)
可以看到通过最小化交叉熵的角度推导出来的结果和使用最大化似然得到的结果是一致的
(3)最后一个角度为BP过程:当使用平方误差损失函数时,最后一层的误差为δ(l)=−(y−a(l))f′(z(l))\delta^{(l)}=-\left(y-a^{(l)}\right) f^{\prime}\left(z^{(l)}\right)δ(l)=−(y−a(l))f′(z(l)),其中最后一项为f′(z(l))f^{\prime}\left(z^{(l)}\right)f′(z(l)),为激活函数的导数。当激活函数为Sigmoid函数时,如果z(l)z^{(l)}z(l)的值非常大,函数的梯度趋于饱和,即f′(z(l))f^{\prime}\left(z^{(l)}\right)f′(z(l))的绝对值非常小,导致δ(l)\delta^{(l)}δ(l)的取值也非常小,使得基于梯度的学习速度非常缓慢;
当使用交叉熵损失函数时,最后一层的误差为δ(l)=f(zk(l))−1=ak~(l)−1\delta^{(l)}=f\left(z_{k}^{(l)}\right)-1=a_{\tilde{k}}^{(l)}-1δ(l)=f(zk(l))−1=ak~(l)−1,此时导数是线性的,因此不存在学习速度过慢的问题.
引入交叉熵损失函数目的是解决一些实例在刚开始训练时学习得非常慢的问题,其主要针对激活函数为Sigmod 函数,如果在输出神经元是S型神经元时,交叉熵一般都是更好的选择,交叉熵无法改善隐藏层中神经元发生的学习缓慢,交叉熵损失函数只对网络输出明显背离预期时发生的学习缓慢有改善效果, 交叉熵损失函数并不能改善或避免神经元饱和,而是当输出层神经元发生饱和时,能够避免其学习缓慢的问题。
6. 合页损失(Hinge Loss)
合页损失(Hinge Loss)是另外一种二分类损失函数,适用于 maximum-margin 的分类,支持向量机Support Vector Machine (SVM)模型的损失函数本质上就是Hinge Loss + L2正则化。合页损失的公式如下:
Jhinge=∑i=1Nmax(0,1−sgn(yi)y^i)J_{h i n g e}=\sum_{i=1}^{N} \max \left(0,1-\operatorname{sgn}\left(y_{i}\right) \hat{y}_{i}\right) Jhinge=i=1∑Nmax(0,1−sgn(yi)y^i)
下图是yyy为正类,即sgn(y)=1sgn(y)=1sgn(y)=1时,不同输出的合页损失示意图:

可以看到当yyy为正类时,模型输出负值会有较大的惩罚,当模型输出为正值且在(0,1)(0,1)(0,1)区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的,并且对于预测对了但是置信度不高的也会给一个惩罚,只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界,使得所有数据点被这个边界正确地、高置信地被分类
7. 0/1损失函数
0/1损失函数是指预测值和目标值不相等为1, 否则为0:
L(Y,f(X))={1,Y≠f(X)0,Y=f(X)L(Y, f(X))=\left\{\begin{array}{l}1, Y \neq f(X) \\ 0, Y=f(X)\end{array}\right. L(Y,f(X))={1,Y=f(X)0,Y=f(X)
(1)0/1损失函数直接对应分类判断错误的个数,但是它是一个非凸函数,不太适用
(2)感知机就是用的这种损失函数。但是相等这个条件太过严格,因此可以放宽条件,即满足∣Y−f(x)∣<T|Y-f(x)|< T∣Y−f(x)∣<T则认为相等:
L(Y,f(X))={1,∣Y−f(X)∣≥T0,∣Y=f(X)∣<TL(Y, f(X))=\left\{\begin{array}{l}1,|Y-f(X)| \geq T \\ 0,|Y=f(X)|<T\end{array}\right. L(Y,f(X))={1,∣Y−f(X)∣≥T0,∣Y=f(X)∣<T
8. 指数损失
指数损失函数的标准形式如下:L(Y,f(X))=exp(−Yf(X))L(Y, f(X))=\exp (-Y f(X))L(Y,f(X))=exp(−Yf(X))
Adaboost中使用了指数损失函数,李航书中证明了:Adaboost算法是前向分步算法的特例,模型是由基本分类器组成的加法模型,损失函数为指数函数.
9. 对数损失/对数似然损失(Log-likelihood Loss)
log对数损失函的标准形式如下:L(Y,P(Y∣X))=−logP(Y∣X)L(Y, P(Y \mid X))=-\log P(Y \mid X)L(Y,P(Y∣X))=−logP(Y∣X)
log对数损失函数能非常好的表征概率分布,在很多场景尤其是多分类,如果需要知道结果属于每个类别的置信度,那它非常适合;健壮性不强,相比于hinge loss对噪声更敏感
10. Smooth L1 Loss
SmoothL1(x)={0.5x2if ∣x∣<1∣x∣−0.5otherwise \operatorname{Smooth} L_{1}(x)=\left\{\begin{array}{cc}0.5 x^{2} & \text { if }|x|<1 \\ |x|-0.5 & \text { otherwise }\end{array}\right. SmoothL1(x)={0.5x2∣x∣−0.5 if ∣x∣<1 otherwise
其中,x=f(xi)−yix=f\left(x_{i}\right)-y_{i}x=f(xi)−yi为真实值和预测值的差值。
相关文章:

深度学习中的损失函数
文章目录一. Loss函数1. 均方差损失(Mean Squared Error Loss)2. 平均绝对误差损失(Mean Absolute Error Loss)3.(Huber Loss)4. 分位数损失(Quantile Loss)5. 交叉熵损失࿰…...

English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [ð] Day29 2023.3.21 周二
English Learning - L2 语音作业打卡 辅音咬舌音 [θ] [] Day29 2023.3.21 周二💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [θ]…...

【原始者-综述】
目录知识框架No.1 AcwingNo.2 LeetcodeNo.3 PTANo.4 蓝桥No.5 牛客网No.6 代码随想录知识框架 No.1 Acwing 那就点击这里转向自己的Acwing题解咯 单调栈,动态规划,贪心,回溯,二叉树,站与队列,双指针&#…...

C++内存模型
目录 一.内存分区 二,分区顺序 1 程序运行前 2 程序运行后 3.new操作符 一.内存分区 内存分区意义:不同区域存放的数据,赋予不同的生命周期, 给我们更大的灵活编程 内存可以分为以下几个区: 代码区:存放函数体的二进制代码…...
八股+面经
文章目录项目介绍Java基础MapHashMap v.s Hashtable(5点)ConcurrentHashMap v.s Hashtable(2点)代理模式1. 静态代理2. 动态代理2.1 JDK 动态代理机制2.2 CGLIB 动态代理机制Java并发线程volatilesynchronized线程池JVM类加载机制垃圾回收(GC)1. 引用类型…...
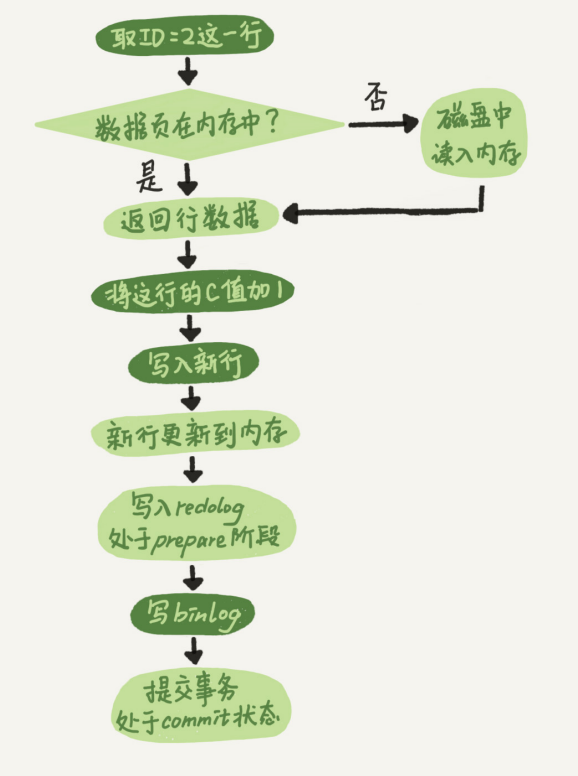
MySQL更新数据流程
1.mysql三种重要日志 redo log(重做日志):存在于引擎层,物理存储,通过设置innodb_flush_log_at_trx_xommit1 让其持久化到磁盘,保证引擎的crash-safe能力,遵从WAL技术(Write-Ahead …...
测试开发进阶系列课程
测试开发系列课程1.完善程序思维--------案列:图书管理系统的创建**(一)图书管理系统的创建**1.完善程序思维--------案列:图书管理系统的创建 (一)图书管理系统的创建 1.在main中写入主函数,…...
 对象树管理)
Qt源码阅读(三) 对象树管理
对象树管理 个人经验总结,如有错误或遗漏,欢迎各位大佬指正 😃 文章目录对象树管理设置父对象的作用设置父对象(setParent)完整源码片段分析对象的删除夹带私货时间设置父对象的作用 众所周知,Qt中,有为对象设置父对象…...
【Python入门第四十二天】Python丨NumPy 数组裁切
裁切数组 python 中裁切的意思是将元素从一个给定的索引带到另一个给定的索引。 我们像这样传递切片而不是索引:[start:end]。 我们还可以定义步长,如下所示:[start:end:step]。 如果我们不传递 start&…...
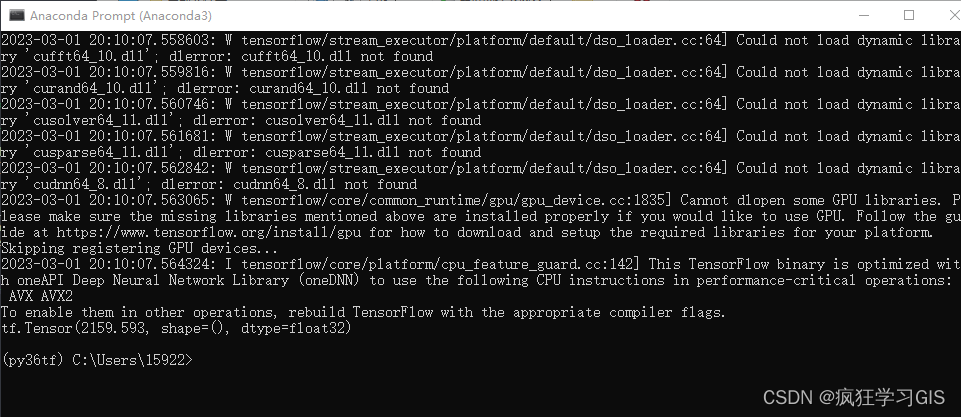
Anaconda配置Python新版本tensorflow库(CPU、GPU通用)的方法
本文介绍在Anaconda环境中,下载并配置Python中机器学习、深度学习常用的新版tensorflow库的方法。 在之前的两篇文章基于Python TensorFlow Estimator的深度学习回归与分类代码——DNNRegressor(https://blog.csdn.net/zhebushibiaoshifu/article/detail…...
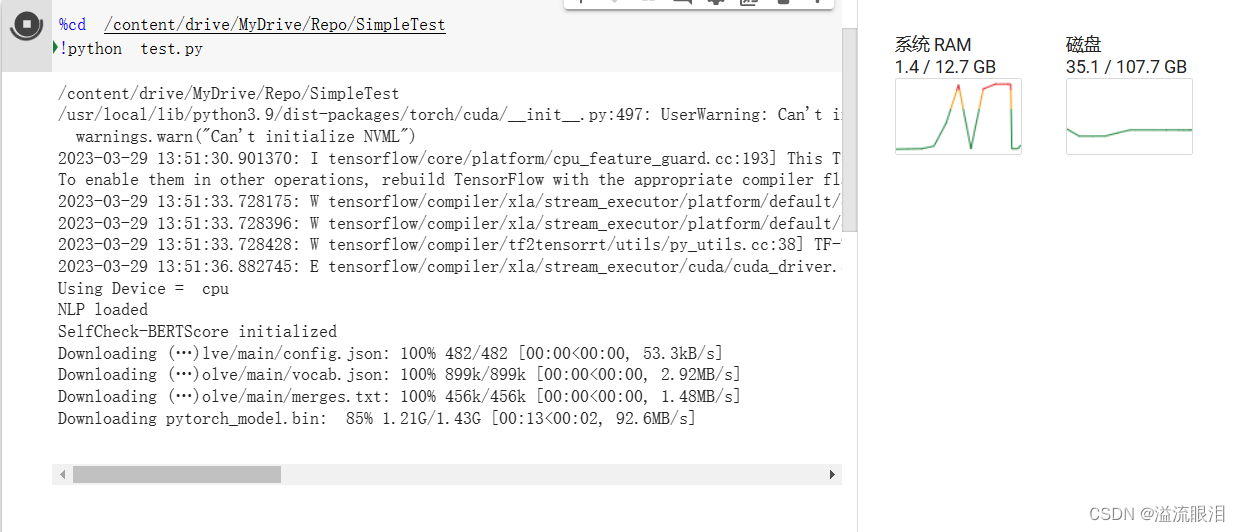
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决
加载模型时出现 OSError: Unable to load weights from pytorch checkpoint file 报错的解决报错信息原因查明网传解决措施好消息我的解决措施报错信息 查了下,在网上还是个比较常见的报错 一般为加载某模型时突然报错 原因查明 一般为下载某个 XXX_model.bin 的…...

sessionStorage , localStorage 和cookie的区别
一.sessionStorage(临时存储)sessionStorage是HTML5中新增的Web Storage API之一,用于在浏览器中存储键值对数据,与localStorage类似,但是sessionStorage存储的数据在会话结束时会被清除。可以通过以下方式使用sessionStorage:存储…...

C# 实例详解委托之Func、Action、delegate
委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,这个文章主要就这三种委托的用法通过实例展开讲解。 【Func】:Func是带返回值的委托: 原型函数如下(以下展示的…...
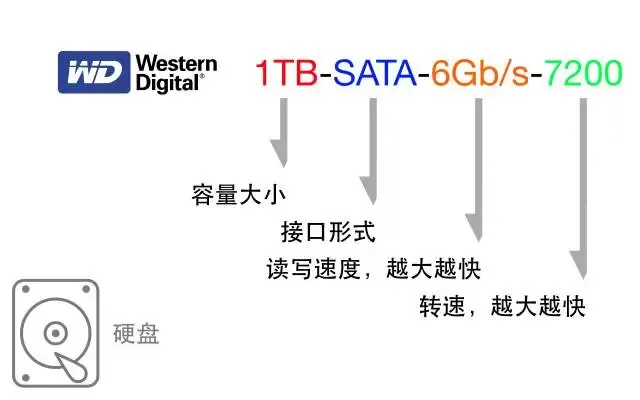
如何选电脑
1、CPU(中央处理器) 怎么看CPU型号:CPU:系列-代数等级核心显卡型号电压后缀 例如CPU:i7-10750H : 1、系列:Intel的酷睿i3、i5、i7、i9这四个系列的CPU,数字越大就代表越高端。 2、代数:代表…...

SpringBoot项目创建
如果使用spring的源地址创建项目失败,就使用 阿里云的springBoot项目创建地址:https://start.aliyun.com/ 1.new 一个新的项目: 2.选择合适的版本java的JDK和maven项目 3.选择spring web依赖 4.直接finish 5. 删除无用的包,然后…...

神经衰弱该如何判断?确诊为神经衰弱,日常要做好这7大护理!
神经衰弱是由于长时间处于紧张或者压力的情况下导致精神出现兴奋或者疲乏现象而伴随着一系列症状。如情绪烦恼、容易激怒、睡眠障碍、肌肉出现紧张性疼痛等,生活中有很多人在自己的不到休息或者遇到强大打击时就会嘲笑自己患上神经衰弱。甚至一些会盲目采取措施&…...

Linux之进程替换
进程替换1.什么是进程替换2.替换函数2.1 execl函数2.2 execv函数2.3 execlp函数2.4 execvp函数2.5 在自己的C程序上如何运行其他语言的程序?2.6 execle 函数2.7 小结3.一个简易的shell1.什么是进程替换 fork()之后,父子各自执行父进程代码的一部分&…...

关于清除浮动
浮动最早是用来做图文排版,为了让块级元素同行显示,而html中块元素是有自己的排列规则,一般独占一行。所以有了浮动元素,一旦元素浮动了就会脱离文档流,产生问题。怎么去清除浮动:(1)…...

Uber H3 index 地图索引思考
H3 是 uber 设计的六边形空间索引,go 语言操作包是 h3-go,可以通过经纬度获取所在的 h3 六边形边界,每个经纬度对应的六边形都是确定的,每个六边形唯一对应了一个 h3index。在业务开发中,我们可以通过 h3index 来对地理…...

多线程的几种状态
Java-多线程的几种状态🔎1.NEW( 系统中线程还未创建,只是有个Thread对象)🔎2.RUNNABLE( (就绪状态. 又可以分成正在工作中和即将开始工作)🔎3.TERMINATED(系统中的线程已经执行完了,Thread对象还在)🔎4.TIMED_WAITING(指定时间等待…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
