【贪心算法】贪心算法
贪心算法简介
- 1.什么是贪心算法
- 2.贪心算法的特点
- 3.学习贪心的方向

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.什么是贪心算法
与其说是贪心算法,不如说是贪心策略。
贪心策略:解决问题的策略( 局部最优 —> 全局最优)。
- 把解决问题的过程分为若干步;
- 解决每一步的时候,都选择当前看起来 “最优的” 解法;
- “希望” 得到全局最优解。
接下来我们举三个例子重点突然我们的贪心策略。
例一:找零问题
假设顾客拿着50块钱去买一瓶4块钱的饮料,你需要找顾客46块钱。此时你只有面额20元、10元、5元、1元 若干个纸币。我们要的是用最少的张数完成找零。
我给你找46块钱肯定是一张一张给你凑成46块钱。解决问题的时候整个问题就分为若干步,若干步就是一张一张的给你找。然后解决每一步的时候都选择当前看起来 “最优的” 解法。
当开始凑46块钱的时候,刚开始肯定不会拿最小的1块钱,我想的是最少的张数,那应该是最快的凑够46块钱。所以第一次肯定选择20块。接下来在凑26块钱,然后凑26块钱,我依旧选择当前看起来最优的还是20块钱。接下来凑6块钱,20和10就不要考虑了,然后选5块钱,接下来在选1块钱,最后正好可以凑够46块钱。

回顾找零过程非常符合贪心策略,每次找钱都选择当前能选择的最大面额,选择u最大面额就能用最少的张数凑成46块钱。
例二:最小路径和
我们在动态规划遇到这道题。我想从左上角到达右下角,然后每次走只能向下走或者向右走。每个格子都是路径,问从左上角达到右下角最小路径和是多少?

这里已经把问题拆分若干个了,从起点一步一步走就是。每一步走的时候都选择当前看起来 “最优的” 解法。从左上角开始走最终走到右下角贪心路径和是10 。

但是可能会有个异或,这个10好像不对,我们直接观察最小的路径和是7。现在先不管正确解法是什么,我们先搞懂什么是贪心策略。
例三:背包问题
物品编号从1~3,每个物品都有体积和价值。此时你手里还有一个最大容量为8的背包。每个物品都有无穷多个。然后问从这些物品种挑选一些物品放背包里,你所挑选东西的最大价值是多少?

这道题限制条件有点多,所以此时我们可能会有非常多的贪心策略。
比如只考虑体积这个限制条件,往背包装的话,肯定会选择体积最小的往背包里装,因为装的多价值可能更大。那只考虑体积的贪心策略的最大价值是8

还有只考虑价值,不是让价值最大吗,那就疯狂装价值最大的,但是因为背包容量的限制,只能装一个价值为10的1号物品。然后去装价值为7的2号物品,但是背包装不下,所以接下来考虑价值为1的3号物品。在这种贪心策略下的最大价值是13

甚至还可以考虑单位体积价值,因为2最大但是因为容量的限制只能装一个1号物品,然后考虑1.75但是装不下,然后就考虑3号物品,你会发现这个策略和只考虑价值的策略是一样的。

虽然上面想了三种贪心策略,但是细心发现这三种策略都错,因为如果最大容量是8的话,那装两个2号物品的最大价值是14,比上面的都大。
虽然最后两个例子贪心并没有解决问题,但是希望已经搞懂什么是贪心策略,就是 贪婪 + 鼠目寸光!说白了只考虑眼前的最优解并不考虑全局的最优解,然后通过眼前的最优解,“希望” 得到全局最优解。但是你会发现鼠目寸光并不一定能得到最后的结果。但是例子又是正确的,为什么正确?待会我们证明一下。
2.贪心算法的特点
1.贪心策略的提出
- 贪心策略的提出是没有标准以及模板的
- 可能每一道题的贪心策略都是不同的
2.贪心策略的正确性
因为有可能 “贪心策略” 是一个错误的方法,正确的贪心策略,我们是需要 “证明的”。
想证明一个贪心策略是错的还是挺简单的,举一个反例就行了。就比如例二 更短的路径和是7,例三 选择两个2号物品价值是最大的。这样就把之前的贪心策略全部都给推翻了。所以想说一个贪心策略是错的还是挺简单的。但是例一 找零问题每次都去选可选的面额最大的就能用最少的张数凑成46块钱,如何证明它是对的呢?
不能说凭感觉,此时看这样一个例子,比如还是凑46,但是现在你的面额是 [20、18、10、5、1],如果依旧按照贪心策略,你会选择两张20元的、一张5元的、一张1元的。但是由于此时有18块钱,我可以选两张18元的,再选一个10元的,才三张就能凑46元。然后你刚刚的贪心就不对了。所以不能说凭感觉,一定要有严格的证明。
常用的证明方法:数学中见过的所有证明方法。
证明:找零问题
[20、10、5、1]
我们先不管策略以及最优解是什么,我们先证明一个性质
假设最优解用了20块钱A张、10块钱B张、5块钱C张、1块钱D张,此时我们先证明一个性质B、C、D是有取值范围的。
先考虑B,B的取值范围有三种:B > 2, B = 2,B < 2
为什么考虑2,因为2张10可以凑成一张20。所以就把B分为>2,=2,<2,三种情况考虑。

我们很好证明前两种情况不是B的最优解,如果想用10,B用的数目超过2张,那么任意两种10都可以用一张20替换,那用20来代替10绝对是比刚刚用两种10块更优的。所以B绝对不可能超过2。

同理B=2也是不可能存在的,原因和上面一样,如果B用了两种10块的,那直接用一张20的替换不是更优的。

由此可以得到一个性质,在最优解中,B的张数绝对是小于2的或者可以说的小于等于1。在最优解中B最多就是一张,要么没有。

同理C是和B一样的,要么C > 2、C = 2、C < 2,最终在最优解中,C的数目最多1张,要么没有。

同理D,因为5张D才可以凑出来一张C,D还是分三种情况:D > 5、D = 5、D < 5,
同理前面两种是不存在的,D超过5张不如用一张C,D等于5张也是不如用一张C,所以D < 5 或者 D 小于等于 4

这是我们证明之前得到的性质,10块钱不超过1张,5块钱不超过1张,1块钱不超过4张。
接下来我们证明方法就是等效法。
设贪心策略最后用的张数是 [a、b、c、d],最优解 [A、B、C、D]。
接下来我们只要证明出来 a = A,b = B,c = C,d = D。那我们就可以说我们贪心就是最优解。
先证明第一个a,回忆一下我们的贪心[a、b、c、d]怎么来的,我们的贪心策略是能用a就用a,直到a不能用了,在用b。所以用这个贪心策略可以得到 a >= A,绝对不可能是 a < A,如果小了就不是贪心策略,因为我们贪心策略就是能用20就尽量用20,所以a >= A。

然后我们还可以证明 a 不可能大于 A,如果 a > A,说明A比较小,别忘了整个钱数是不变的,如果A比较小,那么少的20块钱就会让B、C、D去凑,你会发现根本凑不出来,注意刚才的性质10块钱不超过1张,5块钱不超过1张,1块钱不超过4张,所能凑出来最大的钱是10 + 5 + 4 = 19,根本凑不出20。如果 a 不能大于 A。
因此得到一个结论: a = A

当 a = A,那 b c d 和 B C D 所凑的钱是一样的。 当凑的钱是一样的时候, 我们可以得到 b >= B,因为贪心我们会尽可能的选择10块钱,此时 b >= B ,同理我们也可以证明 b 不可能大于 B,原因和之前的一样,如果B小的话,它会让C和D凑10块钱,但是C和D凑不出来10块钱,C最多一张5块钱,D最多四张1块钱,5 + 4 = 9 最多凑9块钱,根本凑不出10块钱,所以 b 不可能大于 B。
因此 b = B

同理 c = C ,那 d 自然等于 D。

我们严格证明出来贪心策略和最优解是一致的,因此贪心策略得到的结果绝对是最优解。
3.学习贪心的方向
遇到不会的贪心题,很正常,把心态放平。
-
前期学习的时候,把重点放在贪心的策略上,把这个策略当成经验吸收。往后遇到相同类型的题目时可以用经验去解决这道问题。
-
当知道贪心是正确的时候,要想到如何去证明。
相关文章:

【贪心算法】贪心算法
贪心算法简介 1.什么是贪心算法2.贪心算法的特点3.学习贪心的方向 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励,我们一起努力吧!😃😃 1.什么是贪心算法 与其说是…...

【网络原理】❤️Tcp 常用机制❤️ —— 延时应答,捎带应答, 面向字节流, 异常情况处理。保姆式详解 , 建议收藏 !!!
本篇会加入个人的所谓鱼式疯言 ❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言 而是理解过并总结出来通俗易懂的大白话, 小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的. 🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人…...

Scratch教学案例 —— 制作生日蛋糕
小虎鲸Scratch资源站-免费少儿编程Scratch作品源码,素材,教程分享网站! 简介 在这个教学案例中,我们将使用Scratch制作一个简单而有趣的生日蛋糕动画。通过这个项目,学生可以学习到如何使用Scratch中的基本编程块进行角色控制、造型切换、舞台背景设置以…...

【深度学习】搞懂卷积神经网络(一)
卷积神经网络是一种具有局部连接,权重共享等特性的深层前馈神经网络。一般是由卷积层,池化层,全连接层交叉堆叠而成,使用反向传播算法进行训练。卷积神经网络具有一定程度上的平移,缩放和旋转不变性,较前馈…...

VisionPro - 基础 - 00 模板匹配技术和在VP中的使用 - PMAlign - PatMax - (上)
前言 模板匹配是机器视觉领域,尤其是工业视觉领域内,自动化经常要使用的一个视觉算法应用模式。在VP里面,有几种简单的模版匹配的算子,这里大致介绍一下VP的PatMax。 在视觉应用领域,搜索匹配的特征是经常要用到的方…...

容器镜像同步工具image-migrator
1 概述 image-migrator是一个用于容器镜像同步的可执行二进制命令行工具(不依赖于docker命令),能够自动将基于Docker Registry v2镜像仓库(registry、云厂商容器镜像服务、docker hub、Quay、Harbor )中的镜像迁移到基…...

嵌入式系统中的u-boot、kernel、rootfs的区别与关系
嵌入式系统中的u-boot、kernel、rootfs的区别与关系 1. 总览 在嵌入式Linux系统中,软件架构通常分为四个层次,从低到高依次为: 引导加载程序 (Bootloader):固化在硬件Flash中的引导代码,用于硬件基本配置和内核引导…...

K8s1.28 部署Dashboard获取登录信息
Kubernetes Dashboard 是一个基于 Web 的用户界面,用户可以通过它管理和监控 Kubernetes 集群。它提供了对容器化应用程序的概览、集群资源的状态查看、以及对服务和容器的简单操作管理。 配置 Dashboard 访问的方式: Kubernetes 中的服务类型默认是 C…...

智能化大数据平台引领企业迈向精准决策时代
随着科技的飞速发展,大数据平台正逐步迈向更加智能化和自动化的未来趋势。未来的数据平台不仅仅是一个简单的存储和处理数据的工具,而是一个能够自主学习、优化和做出决策的智能系统。这一转变将极大地改变企业处理数据的方式,提高决策的速度…...

1.3 计算机网络的分类
欢迎大家订阅【计算机网络】学习专栏,开启你的计算机网络学习之旅! 文章目录 前言一、按分布范围分类二、按传输技术分类三、按拓扑结构分类四、按使用者分类五、按传输介质分类 前言 计算机网络根据不同的标准可以被分为多种类型,本章从分布…...

深入剖析protobuf.js之Field类:内部机制、使用实践与高级应用指南
引言 在protobuf.js库中,Field类扮演着极其重要的角色,它定义了消息(Message)中每个字段的元数据和行为。Field类不仅包含字段的类型、编号、规则等基本信息,还负责字段的序列化和反序列化逻辑。本文将对protobuf.js的…...

docker挂载宿主机文件run命令启动报错
背景 使用docker安装mysql8,docker run 命令提示报错 命令: docker run -d \ -p 3306:3306 \ -v ~/docker/mysql8/log/mysqld.log:/var/log/mysqld.log \ -e MYSQL_ROOT_PASSWORD=123456 \ --name mysql8 mysql:8.0.36 报错信息 docker: Error response from daemon: fai…...

Python实现 Socket.IO 的在线游戏场景
博客:Python 实现 Socket.IO 的在线游戏场景 目录 引言 什么是 Socket.IO?Socket.IO 的应用场景Socket.IO 在在线游戏中的优势本文案例概述 Socket.IO 的工作原理 Socket.IO 的事件驱动机制WebSocket 与 Socket.IO 的比较Socket.IO 的握手和连接机制 …...

A+B P1001 A+B Problem
P1001 AB Problem #include <bits/stdc.h> using namespace std; int main(){int a,b;std::cin>>a>>b;std::cout<<ab; }...

git编译安装报错
编译安装步骤 卸载旧的 yum -y remove gitcd /usr/local/src/wget https://www.kernel.org/pub/software/scm/git/git-2.15.1.tar.xztar -vxf git-2.15.1.tar.xzcd git-2.15.1make prefix/usr/local/git allmake prefix/usr/local/git installecho "export PATH$PATH:/usr…...
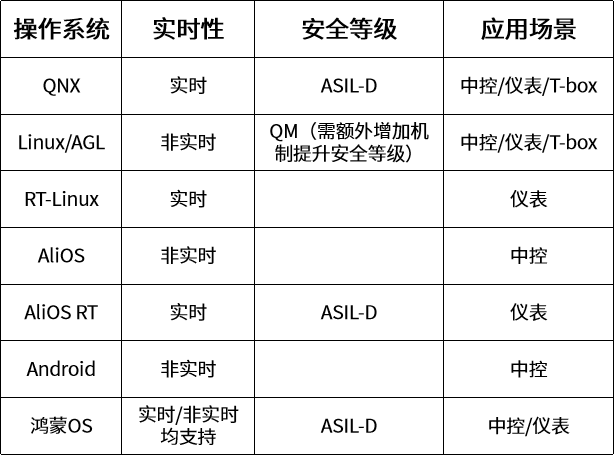
知识|智能网联汽车多域电子电气架构会如何发展?
摘要:随着汽车智能化和网联化技术的快速发展,传统的电子电气架构已经无法满足未来车路云网一体化发展的新需求。本文聚焦于未来智能网联汽车的多域电子电气架构,并从总体设计、硬件系统、通信系统和软件系统四个方面对现有技术进行了详细的综…...

【C++算法】位运算
位运算基础知识 1.基础运算符 << : 左移 >> : 右移 ~ : 取反 & : 按位与,有0就是0 I : 按位或,有1就是1 ^ : 按位异或,(1)相同为0,相异为1(2)无进位相加 2.…...

PMP--一模--解题--101-110
文章目录 11.风险管理--过程--识别风险→实施定性风险分析→实施定量风险分析→规划风险应对→实施风险应对→监督风险101、 [单选] 在项目即将进入收尾阶段时,项目经理发现了一项原来没有考虑到的新风险。该风险一旦发生,可能给最终的可交付成果带来重要…...

为了有了ReentrantLock还需要ReentrantReadWriteLock?
ReentrantLock 和 ReentrantReadWriteLock 是 Java 中的两种不同实现的锁,它们各自适用于不同的应用场景。以下是为什么需要 ReentrantReadWriteLock 的几个原因: 1. 读写分离 ReentrantLock 是一种独占锁,适用于任何线程操作共享资源的场景…...

Vite打包zip并改名为md5sum哈希案例
通常在DevOps CICD流水线部署前端项目时,一般默认都要将dist资源打包为zip,并且把zip名称改为md5sum哈希值(用于文件完整性验证)。 md5sum是什么? md5sum 是一个在 Unix 和类 Unix 系统(如 Linux)中广泛使用的命令行…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
