当前位置：首页 > news >正文

LC并联电路在正弦稳态下的传递函数推导（LC并联谐振选频电路）

news 2026/2/9 2:28:20

LC并联电路在正弦稳态下的传递函数推导（LC并联谐振选频电路）

本文通过 1.解微分方程、2.阻抗模型两种方法推导 LC 并联选频电路在正弦稳态条件下的传递函数，并通过仿真验证不同频率时 v_o(t) 与 v_i(t) 的幅值相角的关系。

电路介绍

已知条件

电路结构如下

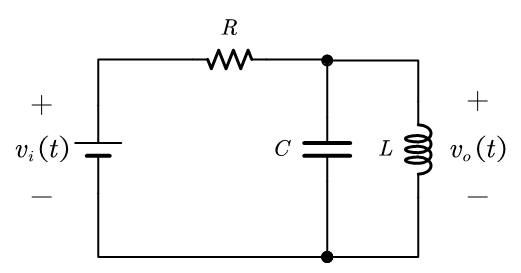
LC并联电路

R：电阻值
C：电容值
L：电感值
输入电源v_i(t)
$v_i(t) = V_Icos(wt)$

其中

$\begin{array}{c} V_I：输入电压的幅值\\ w：输入电源的角频率\\ \frac{w}{2\pi} ：输入正弦信号的频率 \end{array}$

理论计算

1.解微分方程法

解微分方程法常用的四个步骤

根据节点法列写微分方程
找出特解 v_p(t)
找出对应的齐次方程的通解 v_h(t)
根据初始条件计算通解中的常数参数

总的通解为特解+齐次解

$v(t) = v_p(t) + v_h(t)$

$v_{p}(t)$ ，特解

$v_{h}(t)$ ，齐次解

1.1 列些微分方程

前置知识

电容伏安特性： $C\frac{dv}{dt}$
电感伏安特性： $L\frac{di}{dt}$
电感伏安特性的积分形式：
$\frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v \mathrm{d} t \end{aligned} = i$

节点法列方程

$\frac{v_i(t) - v_o(t)}{R} = C\frac{dv_o(t)}{dt} + \frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v_o(t) \mathrm{d} t \end{aligned}$

整理移相得

$\frac{v_i(t)}{R} = C\frac{dv_o(t)}{dt} + \frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v_o(t) \mathrm{d} t \end{aligned} +\frac{v_o(t)}{R}$

等式两边对 t 微分，且带入 $
v_i(t) = V_Icos(wt)
$ 可得：

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ C\frac{dv_o^2(t)}{dt^2} +\frac{1}{R}\frac{dv_o(t)}{dt} + \frac{1}{L}v_o(t) \end{array}$

1.2 找特解

设 v_o(t) 的特解的形式为 $v_p(t) = Acos(wt+\phi)$ ，其中 A 和 ∅ 为要求得未知量，将 v_p(t) 带入微分方程，可得：

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = -Cw^2Acos(wt+\phi) \\ -\frac{1}{R}wAsin(wt+\phi) + \frac{1}{L}Acos(wt+\phi) \end{array}$

利用三角函数的公式可得：

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = -Cw^2Acos(wt)cos(\phi) + \\ Cw^2Asin(wt)sin(\phi)-\frac{wA}{R}sin(wt)cos(\phi) \\ -\frac{wA}{R}cos(wt)sin(\phi) + \frac{A}{L}cos(wt)cos(\phi)\\ -\frac{A}{L}sin(wt)sin(\phi) \end{array}$

合并同类项

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)cos(wt)cos(\phi) + \\ (Cw^2A-\frac{A}{L})sin(wt)sin(\phi)-\\ \frac{wA}{R}sin(wt)cos(\phi) \\ -\frac{wA}{R}cos(wt)sin(\phi) \end{array}$

提公因式

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)(cos(wt)cos(\phi)\\ -sin(wt)sin(\phi))\\ -\frac{wA}{R}(sin(wt)cos(\phi) \\ +cos(wt)sin(\phi)) \end{array}$

利用三角函数公式合并

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)cos(wt+\phi) \\ -\frac{wA}{R}sin(wt+\phi) \end{array}$

根据以下公式

$\begin{array}{c} A_1cos(\theta) - A_2sin(\theta)\\ =\sqrt{A_1^2+A_2^2}sin(\theta-tan^{-1}(\frac{A_1}{A_2})) \end{array}$

可以继续合并化简为：

$\begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ \sqrt{(\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2}*\\ sin(wt+\phi-tan^{-1}(\frac{\frac{A}{L}-Cw^2A}{\frac{wA}{R}})) \end{array}$

令对应位置相等，可得

$\begin{array}{c} \frac{-wV_I}{R} = \sqrt{(\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2} \end{array}$

$\begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array}$

化简上式可得

$\begin{array}{c} \frac{(wV_I)^2}{R^2} = (\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2 \end{array}$

分解因式

$\begin{array}{c} \frac{(wV_I)^2}{R^2} = \\ \frac{A^2}{L^2}+(Cw^2A)^2-2\frac{A}{L}Cw^2A+(\frac{wA}{R})^2 \end{array}$

两边同时乘以 L²R²

$\begin{array}{c} (LwV_I)^2 = A^2R^2+(LRCw^2A)^2\\ -2A^2LR^2Cw^2+(LwA)^2 \end{array}$

提出 A 移项整理得

$\begin{array}{c} A^2 = \frac{(LwV_I)^2}{R^2+(LRCw^2)^2 -2LR^2Cw^2+(Lw)^2} \end{array}$

分式上下同时除以 (Lw)² 得

$\begin{array}{c} A^2 = \frac{V_I^2}{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1} \end{array}$

两边开方，同时只取正解

$\begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array}$

因此，可得 v_p 为

$v_p(t) = A cos(wt + \phi)$

其中：

$\begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array}$

$\begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array}$

1.3 找通解

微分方程对应的齐次方程为

$\begin{array}{c} 0 = C\frac{dv_o^2(t)}{dt^2} +\frac{1}{R}\frac{dv_o(t)}{dt} + \frac{1}{L}v_o(t) \end{array}$

设齐次微分方程解的形式为

$\begin{array}{c} v_h = Ae^{st} \end{array}$

其中 A 和 s 为待确定的参数，带入可得

$\begin{array}{c} 0 = CAs^2e^{st} + \frac{1}{R} sAe^{st} + \frac{1}{L}Ae^{st} \end{array}$

不考虑 A 为 0 的情况，约掉同类项后可得

$\begin{array}{c} 0 = Cs^2 + \frac{1}{R} s + \frac{1}{L} \end{array}$

解得

$\begin{array}{c} s_1 = \frac{-(\frac{1}{R}-\sqrt{\frac{1}{R^2} - \frac{4C}{L}})}{2C} \end{array}$

$\begin{array}{c} s_2 = \frac{-(\frac{1}{R}+\sqrt{\frac{1}{R^2} - \frac{4C}{L}})}{2C} \end{array}$

可得

$\begin{array}{c} v_h = A_1e^{s_1t} + A_2e^{s_2t} \end{array}$

因为 C > 0，L > 0，所以

$\begin{array}{c} (\frac{1}{R^2} - \frac{4C}{L}) < \frac{1}{R^2} \end{array}$

所以
$\begin{array}{c} (\frac{1}{R}-\sqrt{\frac{1}{R^2} - \frac{4C}{L}}) > 0 \end{array}$

所以 s₁ < 0，s₂ < 0

同时，我们讨论的是正弦稳态的情况下的响应，所以 t 趋近于无限长，此时

$A_1e^{s_1t} \rightarrow 0,\qquad A_2e^{s_2t} \rightarrow 0$

所以 v_h = 0。

1.4 根据初始条件确定参数

由于稳态条件下通解为 0，所以这一步不需要了。

1.5 最终的解

至此，用微分方程的方法得到的最终的解为

$v_o(t) = v_p(t) + v_h(t)$

即

$v_o(t) = A cos(wt + \phi)$

其中：

$\begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array}$

$\begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array}$

2.阻抗模型方法

阻抗模型下的电路示意图

2.1 基础知识

电阻的阻抗模型：
$Z_R = R$

电容的阻抗模型：

$Z_C = \frac{1}{jwC}$

电感的阻抗模型：

$Z_L = jwL$

阻抗模型里，输入输出都是复数。

复数输入 V_i 为：

$V_i = V_Ie^{jwt}$

复数输出 V_o 为：

$V_o = V_Oe^{jwt + \phi}$

2.2 计算过程

阻抗模型的适用条件是正弦稳态条件下，可以直接利用分压法进行计算。

$V_o(t) = V_i(t) \frac{Z_C // Z_L}{Z_R + Z_C//Z_L}$

其中

$Z_C // Z_L = \frac{1}{jwC + \frac{1}{jwL}}$

带入，可得

$\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{\frac{1}{jwC + \frac{1}{jwL}}}{R+\frac{1}{jwC + \frac{1}{jwL}}} \end{array}$

分子分母同时除以

$\frac{1}{jwC + \frac{1}{jwL}}$

可得

$\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{R(jwC+\frac{1}{jwL})+1} \end{array}$

继续化简

$\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{j(RwC-\frac{R}{wL})+1} \end{array}$

用复数的角坐标表示

$\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}e^{jtan^{-1}(RwC-\frac{R}{wL})}} \end{array}$

拆分并化简倒数为负指数
$\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{-jtan^{-1}(RwC-\frac{R}{wL})} \end{array}$

将V_i(t)，V_o(t)以及上边的传递函数带入

$\begin{array}{c} V_o(t) = V_i(t) \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} \end{array}$

可得

$\begin{array}{c} V_Oe^{j(wt + \phi)} = \\ V_Ie^{jwt}\frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{-jtan^{-1}(RwC-\frac{R}{wL})} \end{array}$

合并化简可得

$\begin{array}{c} V_Oe^{j(wt + \phi)} =\\ \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{j(wt-tan^{-1}(RwC-\frac{R}{wL}))} \end{array}$

取对应项相等，可得

$\begin{array}{c} V_O= \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}} \end{array}$

$\phi =-tan^{-1}(RwC-\frac{R}{wL})$

根据欧拉公式展开，并取虚部即为要求的时域部分的结果

$v_o(t) = V_Ocos(wt+\phi)$

其中

$V_O= \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}}$

$\phi =-tan^{-1}(RwC-\frac{R}{wL})$

与微分方程计算的结果一致。

绘制函数曲线

传递函数

使用函数绘制工具，以 w 作为变量，绘制传递函数的曲线，并调整 L,R,C 参数，观察不同参数对传递函数的影响，绘制演示如下

下面视频是不同 w 下的幅值变化曲线，可以观察到改变 L 可以调整谐振频率，更改 C 既会影响谐振频率，又会改变通频带的胖瘦（品质因数 Q ），更改 R 只改变胖瘦（品质因数 Q ），不改变谐振频率，在谐振频率处传递函数的幅值为1，说明输出幅值与输入幅值相等。

LC并联电路传递函数幅值随w的变化

下面是不同 w 下的相角变化曲线，上下的角度是正负 90°，改变 R 不会改变谐振频率，在谐振频率相角为 0°。

LC并联电路相角随w的变化

通过曲线图可以看到，电阻会影响品质因数，但是不会改变谐振频率，谐振频率处的输出信号幅值与输入相等，相角偏移为0，说明谐振时，输出与输入完全一致。

谐振频率为：

$\frac{1}{2\pi\sqrt{LC}}$

电路的品质因数 Q 为谐振频率与带宽的比值，带宽是幅值为幅值为谐振点幅值的 0.707 倍时的频率点的差值，因此，波形越瘦，电路的品质因数越高，改变电阻可以改变品质因数。

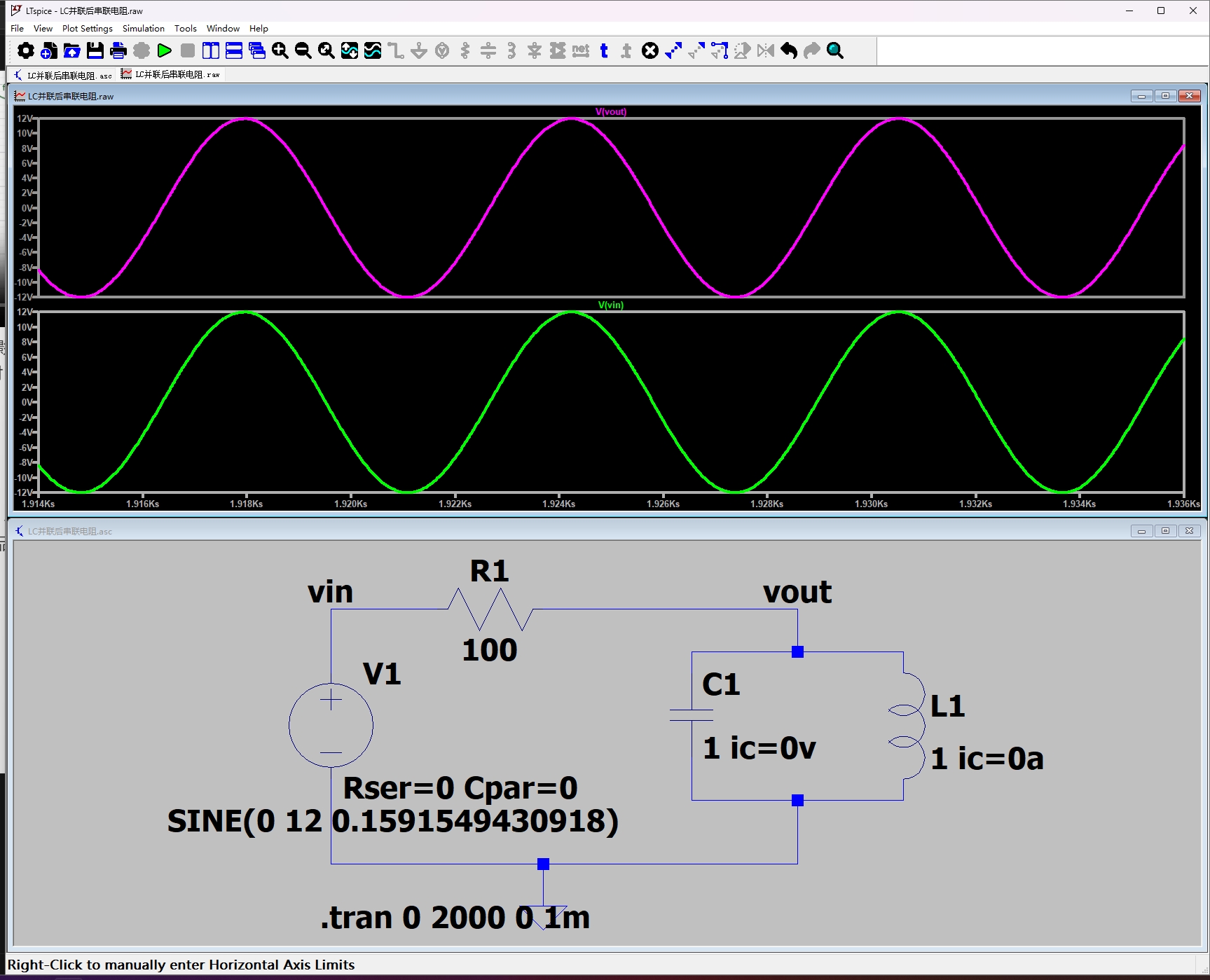
仿真验证

下图仿真在谐振点时输入信号与输出信号完全相同

谐振点仿真结果

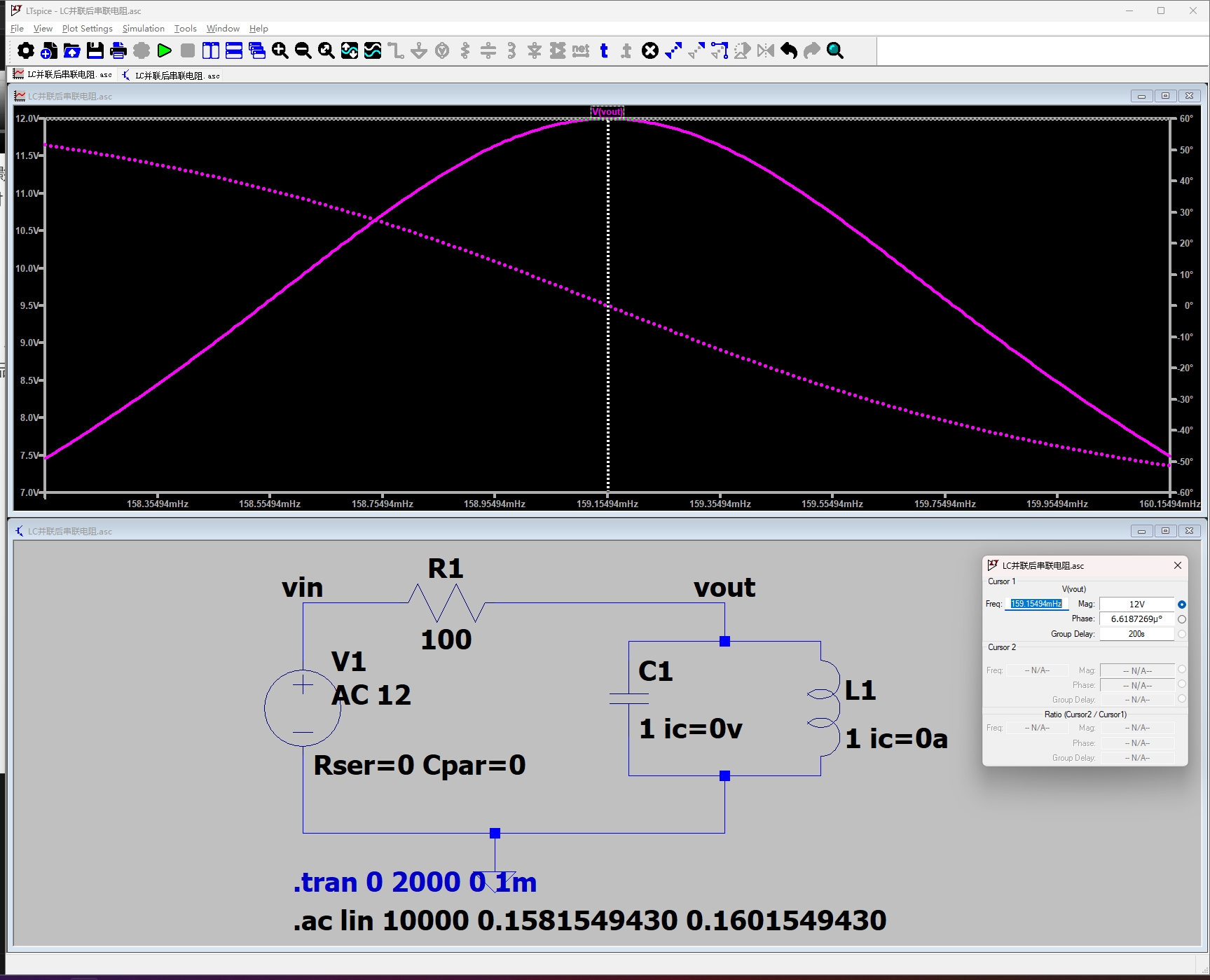
下图是扫频的仿真，可以看到，在谐振点处传递函数幅值最大为 1，且相角为0.

交流扫频仿真结果

参考

正弦稳态：https://www.bilibili.com/video/BV1ts411v7Ep?p=17

阻抗模型：https://www.bilibili.com/video/BV1ts411v7Ep?p=19

电路的 Q 值： https://www.crystal-radio.eu/enlckring.htm#q