R语言进行无序多分类Logistic回归
在临床研究中,接触最多的是二分类数据,如淋巴癌是否转移,是否死亡,这些因变量最后都可以转换成二分类0与1的问题。然后建立二元logistic回归方程,可以得到影响因素的OR值。但有时我们也会接触到多分类结局数据,今天咱们来演示一下怎么使用R语言进行多分类结局逻辑回归分析。

咱们先导入数据和R包
library(here)
library(tidyverse)
library(haven)
library(gtsummary)
library(VGAM)
library(kableExtra)
library(HSAUR)
library(reshape2)
setwd("E:/公众号文章2024年/R无序多分类Logistic回归")
load("hsbdemo.rda")
ms<-hsbdemo

这个数据是高中生毕业后的一个就业计划数据,Prog是结局变量,是个三分类变量,预测变量是ses社会经济地位,其他的是一些协变量。
变量比较多,咱们选出需要的变量,并且把字符变量转成因子
ms <- ms %>% select(ses, prog, female , write ) %>% mutate(across(where(is.labelled), as_factor))

咱们以prog为分类变量,绘制个基线表,了解相关数据分布
ms %>%tbl_summary(by = prog,statistic = list(all_continuous() ~ "{mean} ({sd})", all_categorical() ~ "{n} ({p}%)"),type = list(where(is.logical) ~ "categorical")) %>% modify_caption("**Table 1. Survey Participant Characteristic**") %>%modify_header(label ~ "**Variable**") %>%modify_spanning_header(c("stat_1", "stat_2", "stat_3") ~ "**Baseline tables for three types of projects**") %>%modify_footnote(all_stat_cols() ~ "Mean (SD) or Frequency (%)") %>%bold_labels() %>%as_gt()

我们以academic为参考,建立新的变量
ms <- ms %>% mutate(prog2 = fct_relevel(prog, c("academic", 'general', 'vocation')))
levels(ms$prog2)

更改了参考类别后,咱们使用prog2为结局变量建立无序多分类逻辑回归模型,很多包可以建立这个模型,我这里用vglm包来建,我觉得比较简单点
fit <- vglm(prog2~ ses + write, multinomial, data = ms)
summary(fit)

这样结果就出来啦,seslow:1和seslow:2的这两个系数是针对academic这个结局的
还可以做交互效应的,把交互效应打上去就可以啦,我这里就不弄了。
查看系数和可惜区间
b_mlog <- coef(fit )
ci_mlog <- confint(fit)
b_ci_mlog <- data.frame(b_mlog,ci_mlog) %>%rename("log odds" = b_mlog, "Lower CI" = X2.5.., "Upper CI" = X97.5..)
b_ci_mlog %>% kbl(digits = 2, booktabs = T, caption = "Log odds from multinomial logistic regression") %>%kable_styling(position = "center")

查看各个结局概率的数据
predict.vgam(fit, type = 'response') %>% head(20)

构造一个新数据
ms2 <- data.frame(ses = rep(c("low", "middle", "high"), each = 41), write = rep(c(30:70), 3))
ms2<-predict(fit, newdata = ms2,type = 'response') %>% cbind(ms2)
转化数据
ms3 <- melt(ms2, id.vars = c("ses", "write"), value.name = "probability")

最后绘图
ggplot(ms3, aes(x = write, y = probability, colour = ses)) + geom_line() + facet_grid(variable ~ ., scales = "free")

表明随着write增加,不同的经济基础转向各个计划的概率不同。
参考文献
- https://xianxiongma.github.io/Clinical-model/chapter2/chapter2.html
- https://bookdown.org/drki_musa/dataanalysis/multinomial-logistic-regression.html
相关文章:

R语言进行无序多分类Logistic回归
在临床研究中,接触最多的是二分类数据,如淋巴癌是否转移,是否死亡,这些因变量最后都可以转换成二分类0与1的问题。然后建立二元logistic回归方程,可以得到影响因素的OR值。但有时我们也会接触到多分类结局数据…...

Maven从入门到精通(三)
一、Settings 配置 settings.xml 用来配置 maven 项目中的各种参数文件,包括本地仓库、远程仓库、私服、认证等信息。 全局 settings、用户 setting、pom 的区别: 全局 settings.xml 是 maven 的全局配置文件,一般位于 ${maven.home}/conf…...

Red Hat 和 Debian Linux 对比
原图的作者(https://bbs.deepin.org/post/209759) Red Hat Enterprise Linux https://www.redhat.com/ CentOS Linux https://www.centos.org/ Fedora Linux https://fedoraproject.org/ Debian https://www.debian.org/ Ubuntu https://cn.ubuntu.com/ https://ubuntu.c…...

Axure设计之全屏与退出全屏交互实现
在Axure RP中,设计全屏与退出全屏的交互功能可以极大地提升用户体验,尤其是在展示产品原型或进行演示时。本文将详细介绍如何在Axure RP中通过结合JavaScript代码实现全屏与退出全屏的交互效果。 Axure原型设计web端交互元件库:https://…...

如何测试出自己电脑的网络速度(网速)?
首先电脑上要下载一个这样的一个电脑软件:360安全卫士 1、打开软件之后,选择【网络安全】 2、选择【宽带测速器】 3、点击之后,即可开始检测当前网络速度,等待大概十几秒后会出现结果,如下: 位置①:显示…...

如何利用AI进行有效的科技产品发布
如果你们公司即将推出一款具有颠覆性的软件,你大概已经了解了科技在现代市场中的价值。 但像AI这样的技术不仅仅是有效的产品组成部分,它们还可以帮助将这些产品推向客户(或安装到他们的电脑上)。 Kuno Creative明白AI在科技营销…...

二层、三层网络基本原理
文章目录 二层网络整体拓扑相关配置配置namespace创建switch创建veth设备配置veth的IP启动veth 测试 三层网络配置vm1配置vm2配置 测试 二层网络 我们用Linux bridge模拟现实中的switch,用namespace模拟连接在交换机上的pc 整体拓扑 ------------------ ----…...
全面掌握 Jest:从零开始的测试指南(上篇)
随着JavaScript在前后端开发中的广泛应用,测试已成为保证代码质量的关键环节。 为什么需要单元测试 在我们的开发过程中,经常需要定义一些算法函数,例如将接口返回的数据转换成UI组件所需的格式。为了校验这些算法函数的健壮性,部…...

Go 交叉编译
Mac 下编译 Linux 和 Windows 64位可执行程序 Linux: CGO_ENABLED0 GOOSlinux GOARCHamd64 go build main.go Windows: CGO_ENABLED0 GOOSwindows GOARCHamd64 go build main.go Linux 下编译 Mac 和 Windows 64位可执行程序 Mac: CGO_ENABLED0 G…...

goctl安装失败
今天遇到一个很奇怪的问题 在阿里云的ubuntu服务器上远程安装goctl:go install github.com/zeromicro/go-zero/tools/goctllatest,后面会断开ssh连接,就再也连不上了,connecting with ssh timed out。在阿里云的workbench上连接显…...

DebateGPT:通过多智能体辩论监督微调大模型
人工智能咨询培训老师叶梓 转载标明出处 这些模型的训练通常依赖于资源密集型的人工反馈,这不仅成本高昂,而且耗时。为了解决这一问题,一篇名为《FINE-TUNING LARGE LANGUAGE MODELS WITH MULTI-AGENT DEBATE SUPERVISION》的论文提出了一种…...

【最新综述】基于深度学习的超声自动无损检测(下)
4.Levels of automation 5.Basic axioms for DL-based ultrasonic NDE 在回顾了最新技术和每个自动化级别的贡献之后,我们不难发现,目前的数字语言方法论在不同论文之间存在着很大的差异。例如,有些作者提出了同时处理不同步骤的模型[121]&…...

kali——tshark的使用
目录 前言 使用方法 tshark提取流量为文档 前言 tshark 是一个命令行的网络分析工具,它用于捕获和分析网络流量。它支持多种网络协议,包括 TCP、UDP、ICMP 等。Tshark 可以用于调试网络问题、进行安全审计、分析应用程序性能等。 在 Kali Linux 中&…...
TortoiseSVN图标不显示的解决
解决办法一:修改svn软件的图标设置 1、选中一个文件夹或在桌面空白处,右击进入svn的setting 2、进入setting->Icon Overlays,Status cache选择Default或shell,然后点击应用 3、查看文件,图标可以正常显示 解决办法二:修改注册表的文件夹顺序 问题现象: 1、svn一直…...

Oracle 11gR2打PSU补丁详细教程
1 说明 Oracle的PSU(Patch Set Update)补丁是Oracle公司为了其数据库产品定期发布的更新包,通常每季度发布一次。PSU包含了该季度内收集的一系列安全更新(CPU:Critical Patch Update)以及一些重要的错误修…...
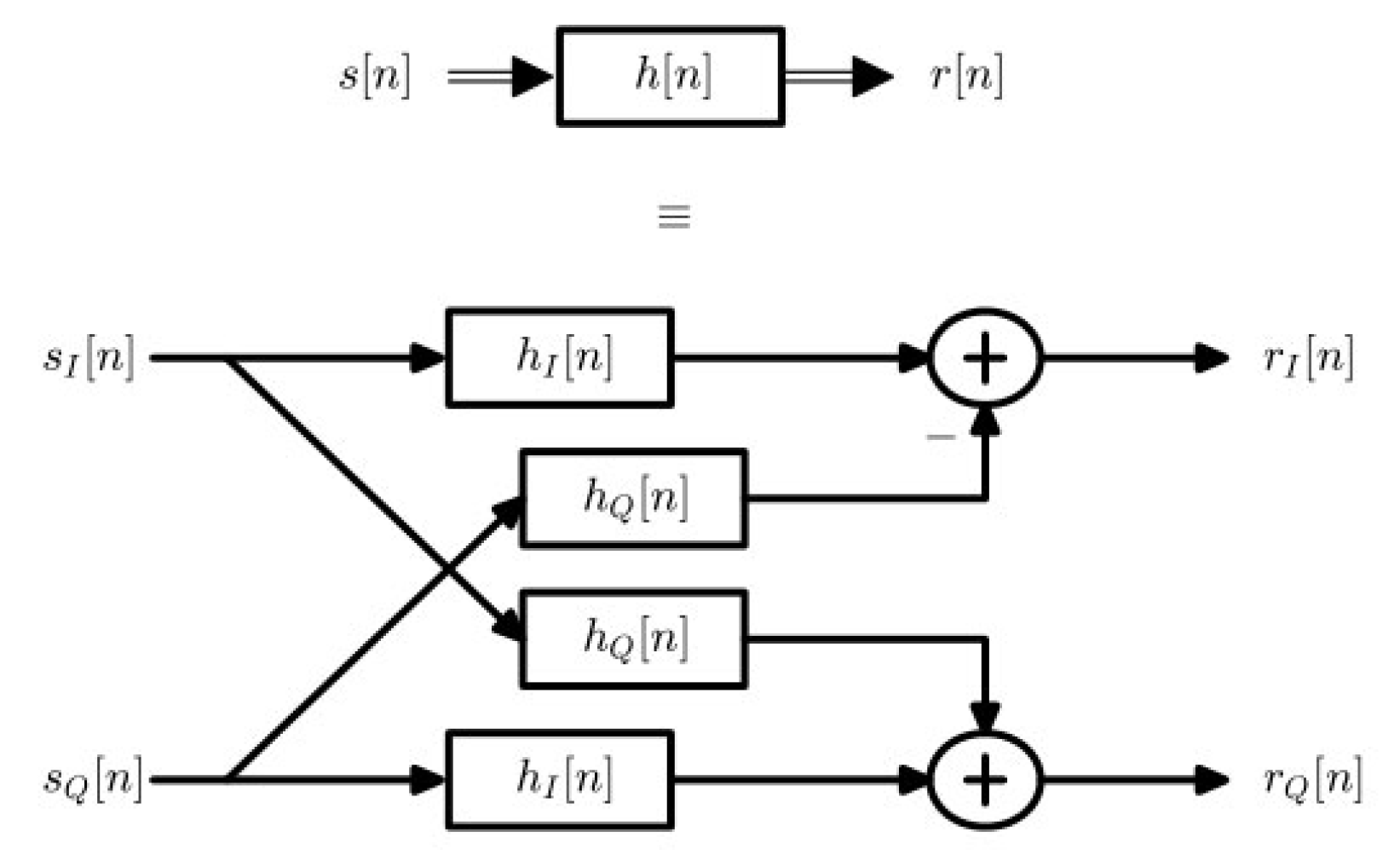
2.4 卷积1
2.4 卷积1 2.4 卷积 在了解了系统及其脉冲响应之后,人们可能会想知道是否有一种方法可以通过任何给定的输入信号(不仅仅是单位脉冲)确定系统的输出信号。卷积就是这个问题的答案,前提是系统是线性且时不变的(LTI&…...

OA项目值用户登入首页展示
1.什么是OA 办公自动化(Office Automation,简称OA)是将现代化办公和计算机技术结合起来的一种新型的办公方式。办公自动化没有统一的定义,凡是在传统的办公室中采用各种新技术、新机器、新设备从事办公业务,都属于办公自动化的领域。通过实现办公自动化,或者说实现数字化…...

如何关闭前端Chrome的debugger反调试
1、禁用浏览器断点 2. 把控制台独立一个窗口...

硬件工程师笔试面试——晶振
目录 13、晶振 13.1 基础 晶振原理图 晶振实物图 13.1.1 概念 13.1.2 工作原理 13.1.3 应用领域 13.1.4 产品类型 13.2 相关问题 13.2.1 晶振的工作原理是什么,它如何保证频率的稳定性? 13.2.2 在工业控制领域,晶振是如何确保精确度的? 13.2.3 晶振的Q值是如何…...
如何用安卓玩Java版Minecraft,安卓手机安装我的世界Java版游戏的教程
安卓手机使用FCL启动器安装我的世界Java版游戏的教程。如何用安卓玩Java版Minecraft 视频教程:https://www.bilibili.com/video/BV1CctYebEzR/ 前言 目前,安卓设备上可以用来运行Java版Minecraft的启动器主要有以下几款: PojavLauncher&a…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
