2.4 卷积1
2.4 卷积1
2.4 卷积
在了解了系统及其脉冲响应之后,人们可能会想知道是否有一种方法可以通过任何给定的输入信号(不仅仅是单位脉冲)确定系统的输出信号。卷积就是这个问题的答案,前提是系统是线性且时不变的(LTI)。
Tips:大概是卷积的意义吧,由输入确定系统的输出。
2.4.1 常规卷积
我们从实际信号和具有实际脉冲响应的LTI系统开始。
假设我们有一个任意信号 s [ n ] s[n] s[n]。然后, s [ n ] s[n] s[n] 可以通过以下逻辑分解为平移单位脉冲的缩放和。将 s [ n ] s[n] s[n] 与一个单位脉冲相乘,脉冲被平移了 m m m 个样本,即 δ [ n − m ] \delta[n - m] δ[n−m]。由于 δ [ n − m ] \delta[n - m] δ[n−m] 在除了 n = m n = m n=m 之外的所有地方都等于 0,这将使得所有的 s [ n ] s[n] s[n] 值在 n ≠ m n \neq m n=m 时乘以 0,而在 n = m n = m n=m 时乘以 1。因此,结果序列将在 n = m n = m n=m 处具有一个脉冲,其值等于 s [ m ] s[m] s[m]。这一过程在图2.6中得到了清晰的说明。
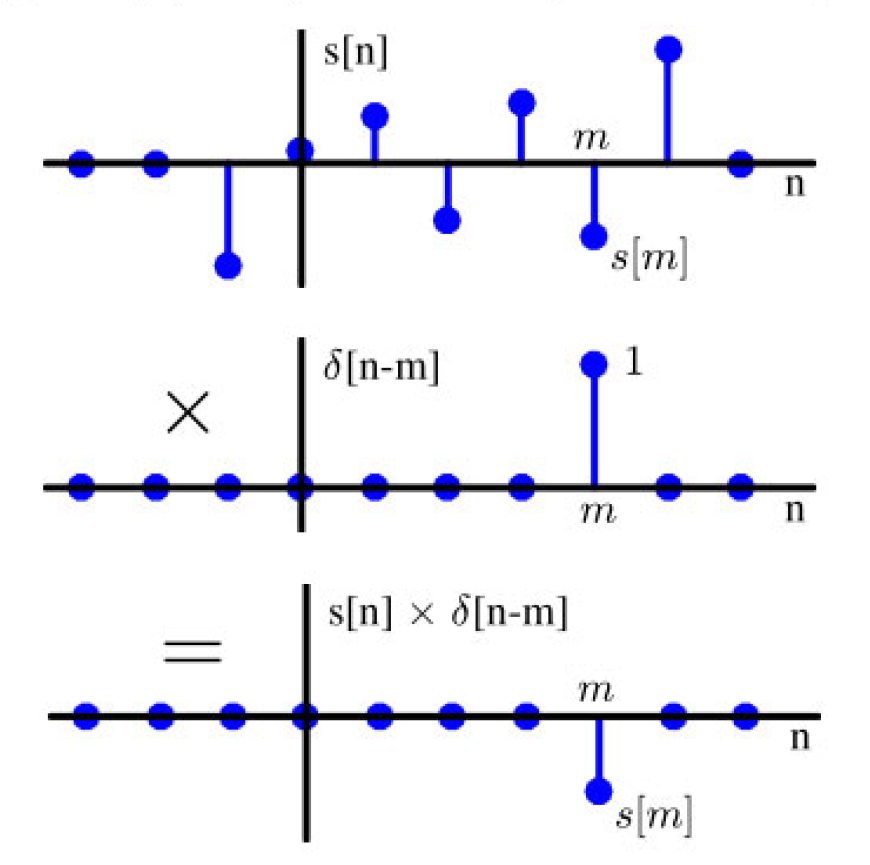
图2.6:将信号 s [ n ] s[n] s[n] 与一个偏移 m m m 的单位冲激信号相乘
可以数学地表示为:
$$s[n] \delta[n - m] = s[m] \delta[n - m]$$用另一个偏移 m ′ m' m′ 重复相同的过程,得到:
$$s[n] \delta[n - m'] = s[m'] \delta[n - m']$$我们说,此时提取出值 s [ m ′ ] s[m'] s[m′]。因此,如果这个乘法过程在所有可能的延迟 − ∞ < m < ∞ -\infty < m < \infty −∞<m<∞ 上重复,并且所有生成的信号相加在一起,结果将是序列 s [ n ] s[n] s[n] 本身。
$$s[n] = \cdots + s[-2]\delta[n+2] + s[-1]\delta[n+1] + s[0]\delta[n] + s[1]\delta[n-1] + s[2]\delta[n-2] + \cdots$$$$= \sum_{m=-\infty}^{\infty} s[m] \delta[n-m] \tag{2.3}$$总结来说,上述方程表明,信号 s [ n ] s[n] s[n] 可以表示为加权单位冲激信号的和,其中每个单位冲激信号 δ [ n − m ] \delta[n - m] δ[n−m] 的幅度为 s [ m ] s[m] s[m]。这样的和的一个例子如图2.7所示。
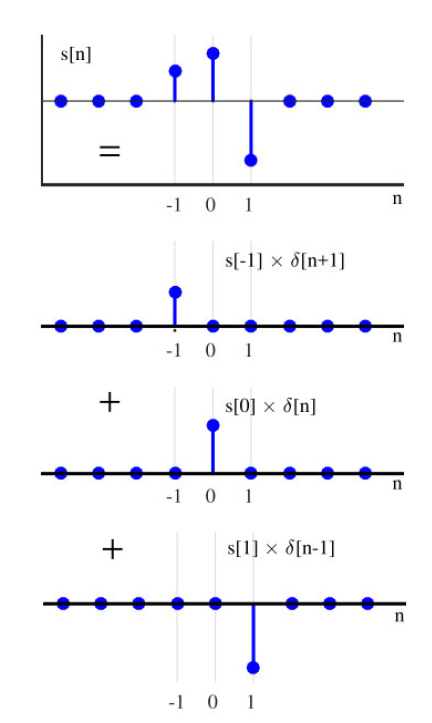
图2.7:将信号 s [ n ] s[n] s[n] 分解为缩放和偏移的冲激信号
LTI系统对缩放单位冲激的响应
现在考虑当这样的信号作为输入给具有冲激响应 h [ n ] h[n] h[n] 的LTI系统时会发生什么。
- 冲激响应 —— LTI系统对单位冲激 δ [ n ] \delta[n] δ[n] 的响应是 h [ n ] h[n] h[n]。
- 由于时不变性,系统对一个移位的单位冲激 δ [ n − m ] \delta[n - m] δ[n−m] 的响应是 h [ n − m ] h[n - m] h[n−m]。
- 由于线性特性的缩放性质,系统对一个缩放并移位的单位冲激 s [ m ] ⋅ δ [ n − m ] s[m] \cdot \delta[n - m] s[m]⋅δ[n−m] 的响应是 s [ m ] ⋅ h [ n − m ] s[m] \cdot h[n - m] s[m]⋅h[n−m]。
- 由于线性特性的加法性质,系统对多个移位单位冲激的响应是各自输出的总和。
输入 —— 输出 对应关系:
| 输入 | 输出 |
|---|---|
| δ [ n ] \delta[n] δ[n] | h [ n ] h[n] h[n] |
| δ [ n − m ] \delta[n - m] δ[n−m] | h [ n − m ] h[n - m] h[n−m] |
| α 1 ⋅ δ [ n − m ] \alpha_1 \cdot \delta[n - m] α1⋅δ[n−m] | α 1 ⋅ h [ n − m ] \alpha_1 \cdot h[n - m] α1⋅h[n−m] |
| α 2 ⋅ δ [ n − m ′ ] \alpha_2 \cdot \delta[n - m'] α2⋅δ[n−m′] | α 2 ⋅ h [ n − m ′ ] \alpha_2 \cdot h[n - m'] α2⋅h[n−m′] |
| α 1 ⋅ δ [ n − m ] + α 2 ⋅ δ [ n − m ′ ] \alpha_1 \cdot \delta[n - m] + \alpha_2 \cdot \delta[n - m'] α1⋅δ[n−m]+α2⋅δ[n−m′] | α 1 ⋅ h [ n − m ] + α 2 ⋅ h [ n − m ′ ] \alpha_1 \cdot h[n - m] + \alpha_2 \cdot h[n - m'] α1⋅h[n−m]+α2⋅h[n−m′] |
这导致了一个输入-输出序列为:
$$\begin{aligned} &+ ....... & \rightarrow & \quad ....... \\ &+ \quad s[-2] \cdot \delta[n + 2] & \rightarrow & \quad s[-2] \cdot h[n + 2] \\ &+ \quad s[-1] \cdot \delta[n + 1] & \rightarrow & \quad s[-1] \cdot h[n + 1] \\ &+ \quad s[0] \cdot \delta[n] & \rightarrow & \quad s[0] \cdot h[n] \\ &+ \quad s[1] \cdot \delta[n - 1] & \rightarrow & \quad s[1] \cdot h[n - 1] \\ &+ \quad s[2] \cdot \delta[n - 2] & \rightarrow & \quad s[2] \cdot h[n - 2] \\ &+ \quad ....... & \rightarrow & \quad ....... \\ \end{aligned}$$- 最终: s [ n ] s[n] s[n] → ∑ m = − ∞ ∞ s [ m ] ⋅ h [ n − m ] \sum_{m=-\infty}^{\infty} s[m] \cdot h[n - m] ∑m=−∞∞s[m]⋅h[n−m]
在上面的过程中,我们推导出了著名的卷积方程,用来描述当输入信号 s [ n ] s[n] s[n] 经过具有冲激响应 h [ n ] h[n] h[n] 的LTI系统时,输出 r [ n ] r[n] r[n] 的表达式:
$$r[n] = \sum_{m=-\infty}^{\infty} s[m] \cdot h[n - m] \quad \tag{2.4}$$其中上面的和式是从 − ∞ -\infty −∞ 到 + ∞ +\infty +∞ 对每个 n n n 计算的。在本文中,卷积操作表示为 ∗ * ∗,即:
$$r[n] = s[n] * h[n] \quad \tag{2.5}$$注意,卷积与相关不同的是:
$$s[n] * h[n] = h[n] * s[n]= \sum_{m=-\infty}^{\infty} h[m]s[n-m] \tag {2.6}$$这可以通过在公式 (2.4) 中代入 p = n − m p = n - m p=n−m 来验证,得到 m = n − p m = n - p m=n−p,因此 ∑ p = − ∞ ∞ s [ n − p ] h [ p ] \sum_{p=-\infty}^{\infty} s[n - p] h[p] ∑p=−∞∞s[n−p]h[p]
注释 2.3 卷积符号
请记住,虽然卷积和信号的共轭都用符号 ∗ * ∗ 表示,但在上下文中总是能看到它们的区别。当用于卷积时,它作为两个信号之间的运算符出现,例如 s [ n ] ∗ h [ n ] s[n] * h[n] s[n]∗h[n]。另一方面,当用于共轭时,它出现在信号的上标处,例如 h ∗ [ n ] h^*[n] h∗[n]。
卷积是一个非常逻辑且简单的过程,但许多数字信号处理(DSP)学习者由于解释方式的缘故,可能会感到困惑。接下来,我们将描述一种传统的方法和另一种更直观的方法来计算卷积输出。
传统方法
在定义卷积方程后,建议通过以下步骤来实现。对于每个特定时间移位 n n n,步骤如下:
-
翻转 (Flip) :将卷积方程排列为
r [ n ] = ∑ m = − ∞ ∞ s [ m ] h [ − m + n ] r[n] = \sum_{m=-\infty}^{\infty} s[m] h[-m + n] r[n]=∑m=−∞∞s[m]h[−m+n]并将冲激响应 h [ m ] h[m] h[m] 视为变量 m m m 的函数。将 h [ m ] h[m] h[m] 关于 m = 0 m = 0 m=0 翻转以得到 h [ − m ] h[-m] h[−m]。
-
移位 (Shift) :为了得到时间移位 n n n 时的 h [ − m + n ] h[-m + n] h[−m+n],将 h [ − m ] h[-m] h[−m] 向右移 n n n 个单位(对于正 n n n),对于负 n n n 则向左移。
-
相乘 (Multiply) :将序列 s [ m ] s[m] s[m] 与序列 h [ − m + n ] h[-m + n] h[−m+n] 逐点相乘,得到乘积序列 s [ m ] ⋅ h [ − m + n ] s[m] \cdot h[-m + n] s[m]⋅h[−m+n]。
-
求和 (Sum) :将上述乘积序列的所有值相加,得到在时间 n n n 时的卷积输出。
-
重复 (Repeat) :对每个可能的 n n n 值重复上述步骤。
两个信号之间卷积的示例
$$s[n] = [2, -1, 1]$$$$h[n] = [-1, 1, 2]$$如图 2.8 所示。在左边的列中,信号 s [ m ] s[m] s[m] 被复制并与 h [ − m ] h[-m] h[−m] 的移位版本叠加,以演示两者之间的重叠,而移位 n n n 则显示在文本框中对应每个 n n n 的值。如果你按照上述步骤操作,你会在图的右边列的文本框中找到结果 r [ n ] r[n] r[n]:
$$r[n] = [-2, 3, 2, -1, 2]$$请注意上面信号表示中的变化。实际的信号 s [ n ] s[n] s[n] 和 h [ n ] h[n] h[n] 是时间索引 n n n 的函数,但卷积方程表示的是这两个信号在时间索引 m m m 下的卷积。另一方面, n n n 用于表示在逐点与 s [ m ] s[m] s[m] 相乘之前,应用于 h [ − m ] h[-m] h[−m] 的时间移位。输出 r [ n ] r[n] r[n] 是时间索引 n n n 的函数,这对应于应用于 h [ − m ] h[-m] h[−m] 的移位。
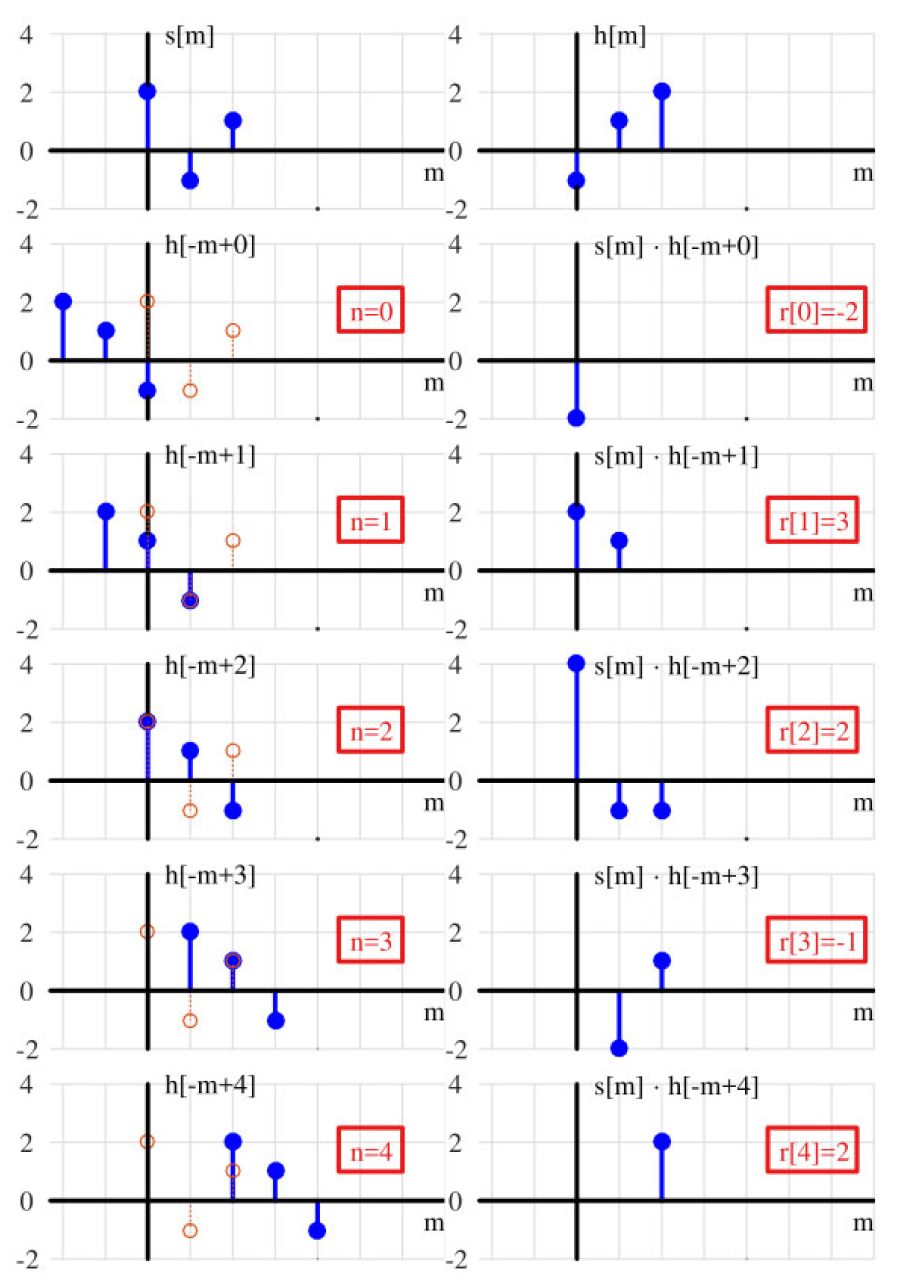
图 2.8: s[n] 和 h[n] 之间卷积的传统方法
接下来,我们转向一种更直观的方法,在这种方法中不需要翻转信号。
直观方法
理解卷积的另一种方法。实际上,它是建立在卷积方程 (2.4) 的推导基础上的,也就是找到输出 r [ n ] r[n] r[n] ,其表达式为:
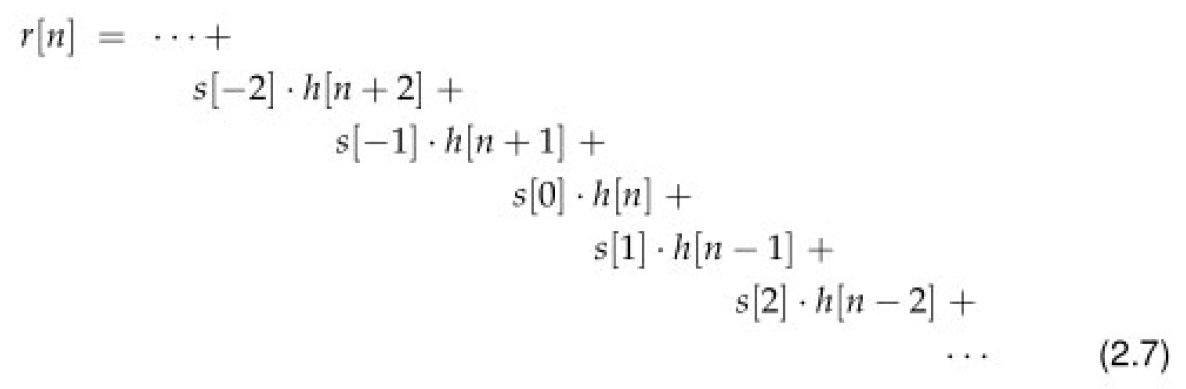
让我们解决与图 2.8 相同的例子,其中
s [ n ] = [ 2 , − 1 , 1 ] s[n] = [2, -1, 1] s[n]=[2,−1,1]
h [ n ] = [ − 1 , 1 , 2 ] h[n] = [-1, 1, 2] h[n]=[−1,1,2]
表 2.1: s[n] 和 h[n] 之间卷积的直观方法
| n n n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| s [ n ] s[n] s[n] | 2 | -1 | 1 | ||
| s [ 0 ] ⋅ h [ n ] s[0] \cdot h[n] s[0]⋅h[n] | 2(-1) | 2(1) | 2(2) | ||
| s [ 1 ] ⋅ h [ n − 1 ] s[1] \cdot h[n-1] s[1]⋅h[n−1] | 0 | -1(-1) | -1(1) | -1(2) | |
| s [ 2 ] ⋅ h [ n − 2 ] s[2] \cdot h[n-2] s[2]⋅h[n−2] | 0 | 0 | 1(-1) | 1(1) | 1(2) |
| 输出 | -2 | 3 | 2 | -1 | 2 |
这种方法如表 2.1 和图 2.9 所示,其结果是通过列求和生成的。从实现的角度来看,这种方法与传统方法没有区别。
注释 2.4:翻转冲激响应的奇特案例
从上面的直观方法来看,翻转实际上根本不存在。翻转仅发生在时间索引 m m m 的世界中,而不是时间索引 n n n 的世界中。而我们在每个 n n n 上找到每个新的输出。
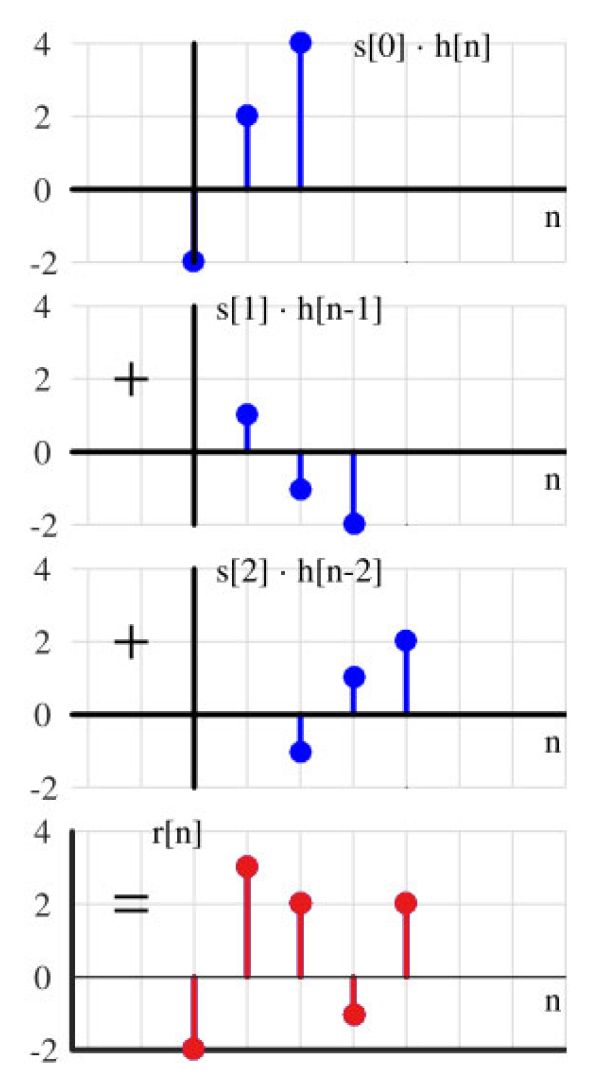
图 2.9: s[n] 和 h[n] 之间卷积的直观方法
现在(NOW),由卷积方程中 n n n 代表,即为自身的移动指针,这个指针实际上在过程中不断变化。时间在滴答流逝,每一次流逝,我们都能进入未来的一个单位,在那里新的输入到来并踢出另一个冲激响应(按输入在该瞬间的幅度缩放)。
由于在现在之前没有实际的输入可施加,我们从时间索引 0 开始。
- 输入 s [ 0 ] s[0] s[0] 在现在(NOW)贡献了 s [ 0 ] ⋅ h [ 0 ] s[0] \cdot h[0] s[0]⋅h[0],这是在时间 0 时的第一个输出采样。实际上,它启动了完整的冲激响应,该响应由其值 ( s [ 0 ] ⋅ h [ 1 ] , s [ 0 ] ⋅ h [ 2 ] , ⋯ ) (s[0] \cdot h[1], s[0] \cdot h[2], \cdots) (s[0]⋅h[1],s[0]⋅h[2],⋯) 缩放,但这些将会发生在未来。
- 新的现在(NOW)是时间索引 1。输入 s [ 1 ] s[1] s[1] 到达并发起了完整的冲激响应,但只有 s [ 1 ] ⋅ h [ 0 ] s[1] \cdot h[0] s[1]⋅h[0] 发生在现在(NOW)。此外,向未来移动了 1 个单位意味着 s [ 0 ] ⋅ h [ 1 ] s[0] \cdot h[1] s[0]⋅h[1] 已在此时到达。因此,时间 1 的输出是 s [ 1 ] ⋅ h [ 0 ] + s [ 0 ] ⋅ h [ 1 ] s[1] \cdot h[0] + s[0] \cdot h[1] s[1]⋅h[0]+s[0]⋅h[1]。
- 以这种方式继续下去,可以看出,在卷积操作期间,现在(NOW) n n n 随着每个滴答向前推进。每个此类 n n n 激活新的冲激响应,当然从 h [ 0 ] h[0] h[0] 开始,因此表达式为 s [ n ] ⋅ h [ 0 ] s[n] \cdot h[0] s[n]⋅h[0]。只有过去输入的那些贡献可以在此时进行汇总,形成当前时刻的贡献。
显然, h [ 1 ] h[1] h[1] 将是从时间 n − 1 n-1 n−1 发生的输入贡献, h [ 2 ] h[2] h[2] 来自 n − 2 n-2 n−2 的输入,依此类推。总而言之, h [ ⋅ ] h[\cdot] h[⋅] 参数的论点不过是每个单独输入从现在(时间索引 n n n)的时间分离——由于这一记忆的存在,它发挥作用以找出每个过去输入对现在的影响。
性质
以下是卷积的一些重要性质。
长度 (Length) :从上图可以看出,当 s [ n ] s[n] s[n] 和 h [ n ] h[n] h[n] 的长度均为 3 个样本时,结果信号 r [ n ] r[n] r[n] 的长度为 5。这是一个通用规则:
$$\text{Length}\{r[n]\} = \text{Length}\{s[n]\} + \text{Length}\{h[n]\} - 1 \tag{2.8}$$这是由于在卷积过程中一个信号完全滑过另一个信号。
第一个样本 (First sample) :从翻转操作可以明显看出,结果的第一个样本位置由下式给出:
$$\text{First sample location}\{r[n]\} = \text{First sample location}\{s[n]\} + \text{First sample location}\{h[n]\} \tag{2.9}$$单位冲激 (Unit impulse) :由于单个单位冲激 δ [ n ] \delta[n] δ[n] 只能生成冲激响应 h [ n ] h[n] h[n] 的单一实例,因此单位冲激对冲激响应的卷积就是冲激响应本身。这个结果是通用的,适用于任何信号 s [ n ] s[n] s[n]。
$$s[n] * \delta[n] = s[n] \tag{2.10}$$复信号的卷积
复信号 s [ n ] s[n] s[n] 输入到具有复冲激响应 h [ n ] h[n] h[n] 的系统中的卷积可以通过以 IQ 形式编写卷积来理解。它以类似的方式定义为
$$r[n] = s[n] * h[n]$$使用复数的乘法规则 I·I - Q·Q 和 Q·I + I·Q
$$I \rightarrow r_I[n] = \sum_{m=-\infty}^{\infty} s_I[m] h_I[n - m] - \sum_{m=-\infty}^{\infty} s_Q[m] h_Q[n - m]$$$$Q \uparrow r_Q[n] = \sum_{m=-\infty}^{\infty} s_Q[m] h_I[n - m] + \sum_{m=-\infty}^{\infty} s_I[m] h_Q[n - m] \tag{2.11}$$这可以写成单个实数卷积的组合。
$$I \rightarrow r_I[n] = s_I[n] * h_I[n] - s_Q[n] * h_Q[n]$$$$Q \uparrow r_Q[n] = s_Q[n] * h_I[n] + s_I[n] * h_Q[n]\tag{2.12}$$由于恒等式 cos A cos B − sin A sin B = cos ( A + B ) \cos A \cos B - \sin A \sin B = \cos (A + B) cosAcosB−sinAsinB=cos(A+B),I 表达式中的负号表明两个对齐轴项的相位实际上是在相加。显然,恒等式仅在可以提取幅度作为公因子的情况下适用于上述方程,但相位对齐的概念仍然成立。同样,恒等式 sin A cos B + cos A sin B = sin ( A + B ) \sin A \cos B + \cos A \sin B = \sin (A + B) sinAcosB+cosAsinB=sin(A+B) 表明在 Q 表达式中,两个交叉轴项的相位也在相加。因此,复卷积可以描述为一个过程:
- 计算 4 个实卷积: I ∗ I I * I I∗I, Q ∗ Q Q * Q Q∗Q, Q ∗ I Q * I Q∗I,以及 I ∗ Q I * Q I∗Q
- 通过相位对齐两个对齐轴卷积 ( I ∗ I − Q ∗ Q ) (I * I - Q * Q) (I∗I−Q∗Q) 来获得 I 分量
- 将两个交叉轴卷积 ( Q ∗ I + I ∗ Q ) (Q * I + I * Q) (Q∗I+I∗Q) 相加,获得 Q 分量
这些计算显示在图 2.10 中,其中双箭头表示复数操作。
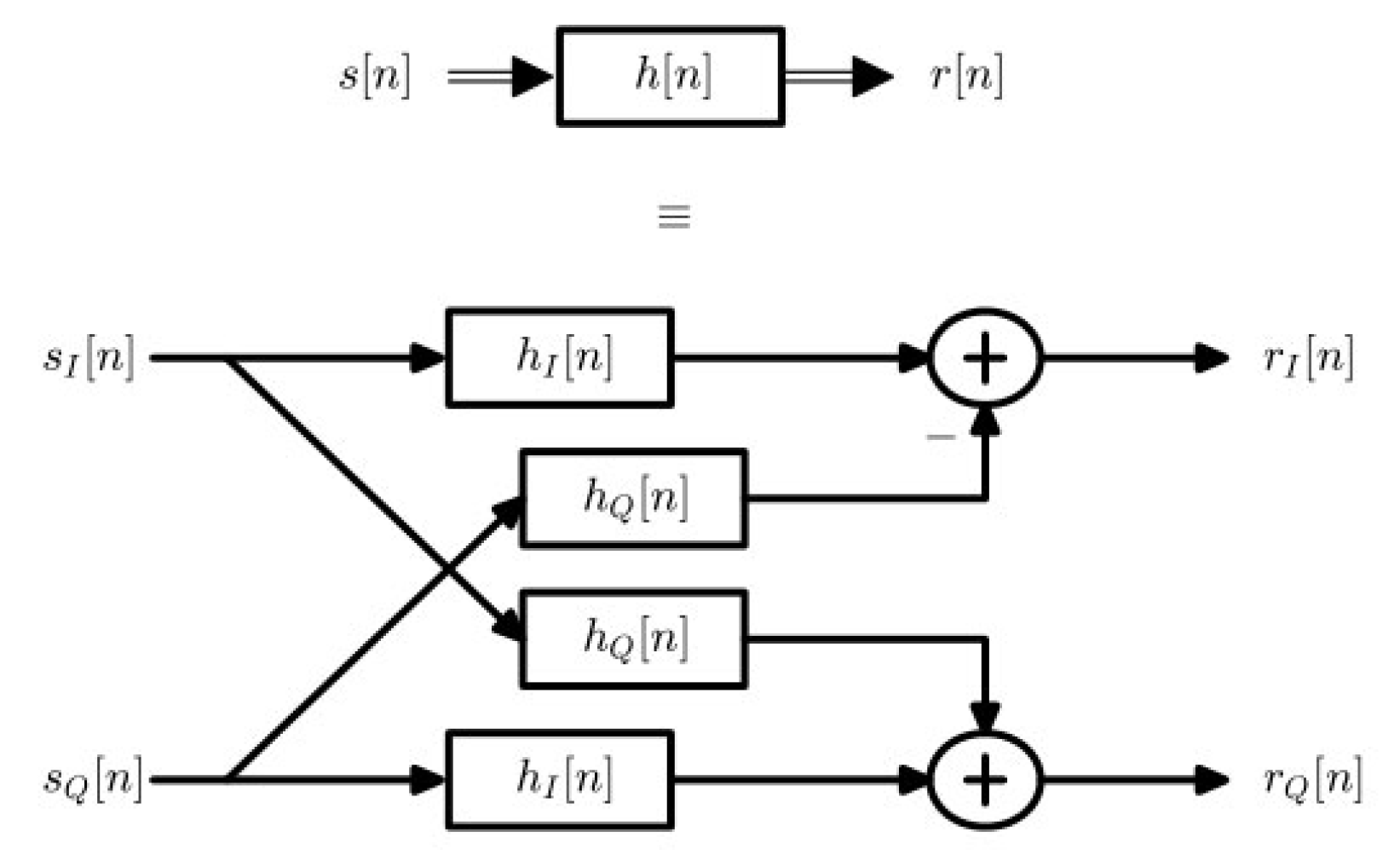
图 2.10: 两个复信号 s [ n ] s[n] s[n] 和 h [ n ] h[n] h[n] 之间的卷积
通过卷积计算相关性
回顾方程 (1.38) 中相关性的定义,如下所示:
$$\text{corr}[n] = \sum_{m=-\infty}^{+\infty} s[m] \cdot h[m-n] = \sum_{m=-\infty}^{+\infty} s[m] \cdot h[-(n-m)]$$因此,相关性可以通过卷积来定义,如下所示:
$$\text{corr}[n] = s[n] * h[-n] \tag{2.13}$$从传统方法的角度来看,两信号之间的相关性可以通过计算卷积的高效方法来实现,只不过没有信号的翻转。这是因为 h [ − n ] h[-n] h[−n] 翻转信号一次,而卷积再次翻转它,从而将原始信号恢复。
从直观方法的角度来看,很明显,负号与现在 − n −n −n 结合,将未来转变为过去,将过去转变为未来。因此,原始信号的最后一个样本最先到达,因为它已经变成了最远的过去。
相关文章:

2.4 卷积1
2.4 卷积1 2.4 卷积 在了解了系统及其脉冲响应之后,人们可能会想知道是否有一种方法可以通过任何给定的输入信号(不仅仅是单位脉冲)确定系统的输出信号。卷积就是这个问题的答案,前提是系统是线性且时不变的(LTI&…...

OA项目值用户登入首页展示
1.什么是OA 办公自动化(Office Automation,简称OA)是将现代化办公和计算机技术结合起来的一种新型的办公方式。办公自动化没有统一的定义,凡是在传统的办公室中采用各种新技术、新机器、新设备从事办公业务,都属于办公自动化的领域。通过实现办公自动化,或者说实现数字化…...

如何关闭前端Chrome的debugger反调试
1、禁用浏览器断点 2. 把控制台独立一个窗口...

硬件工程师笔试面试——晶振
目录 13、晶振 13.1 基础 晶振原理图 晶振实物图 13.1.1 概念 13.1.2 工作原理 13.1.3 应用领域 13.1.4 产品类型 13.2 相关问题 13.2.1 晶振的工作原理是什么,它如何保证频率的稳定性? 13.2.2 在工业控制领域,晶振是如何确保精确度的? 13.2.3 晶振的Q值是如何…...
如何用安卓玩Java版Minecraft,安卓手机安装我的世界Java版游戏的教程
安卓手机使用FCL启动器安装我的世界Java版游戏的教程。如何用安卓玩Java版Minecraft 视频教程:https://www.bilibili.com/video/BV1CctYebEzR/ 前言 目前,安卓设备上可以用来运行Java版Minecraft的启动器主要有以下几款: PojavLauncher&a…...

linux上用yolov8训练自己的数据集(pycharm远程连接服务器)
pycharm如何远程连接服务器,看之前的文章 首先去GitHub上下载项目地址,然后下载预训练模型放到项目主目录下 然后下载数据集,我这有个推荐的数据集下载网站,可以直接下载yolov8格式的数据集(还支持其他格式的数据集&a…...

Git rebase 的使用(结合图与案例)
目录 Git rebase 的使用Git rebase 概念Git rebase 原理rebase和merge的选择 Git rebase 的使用 在 Git 中整合来自不同分支的修改主要有两种方法:merge 以及 rebase Git rebase 概念 **rebase概念:**用来重新应用提交(commits)…...

一文讲懂Mac中的环境变量
你是否曾经因为环境变量配置不当而浪费了宝贵的开发时间?你是否好奇为什么有时候在终端输入命令会提示"command not found",而有时候又能正常运行?如果你是一名Mac用户,并且希望真正掌握环境变量的奥秘,那么这篇文章将为你揭开Mac中环境变量的神秘面纱,帮助你成为一…...

将硬盘的GPT 转化为MBR格式
遇到的问题 在重新安装系统时,磁盘遇到无法空间分配给系统。 解决方式 使用Windows10镜像 U盘安装,选择磁盘时,转换磁盘格式为MBR。然后退出安装程序。 Shift F10# 输入 diskpart# 查看磁盘信息 list disk# 选择需要转换的磁盘࿰…...

C++基于select和epoll的TCP服务器
select版本 服务器 #include <arpa/inet.h> #include <stdlib.h> #include <stdio.h> #include <string.h> #include <unistd.h> #include <sys/socket.h> #include <string> #include <pthread.h> #include <sys/select…...

SpringBoot 读取配置文件的4种方式
文章目录 1. Value 注解读取单个属性2. 使用 ConfigurationProperties 注解3. 通过 Environment 对象读取属性4. 使用 PropertySource 注解加载额外的配置文件 在 Spring Boot 中,application.yml 文件用于配置应用程序的属性,Spring Boot 默认会从 src/…...

【车载开发系列】ParaSoft单元测试环境配置(三)
【车载开发系列】ParaSoft单元测试环境配置(三) 【车载开发系列】ParaSoft单元测试环境配置(三) 【车载开发系列】ParaSoft单元测试环境配置(三)一. 去插桩设置Step1:静态解析代码Step2:编辑Parasoft文件Step3:确认去插桩二. 新增测试用例Step1:生成测试用例Step2:执…...

如何让Threejs的canvas背景透明?
在Three.js中,要让Canvas的背景透明,只显示场景中的模型或物体,有两个关键点: 一、对渲染器(Renderer)进行alpha为true配置; 二、通过CSS设置,使canvas设定为透明背景模式。 以下是代…...
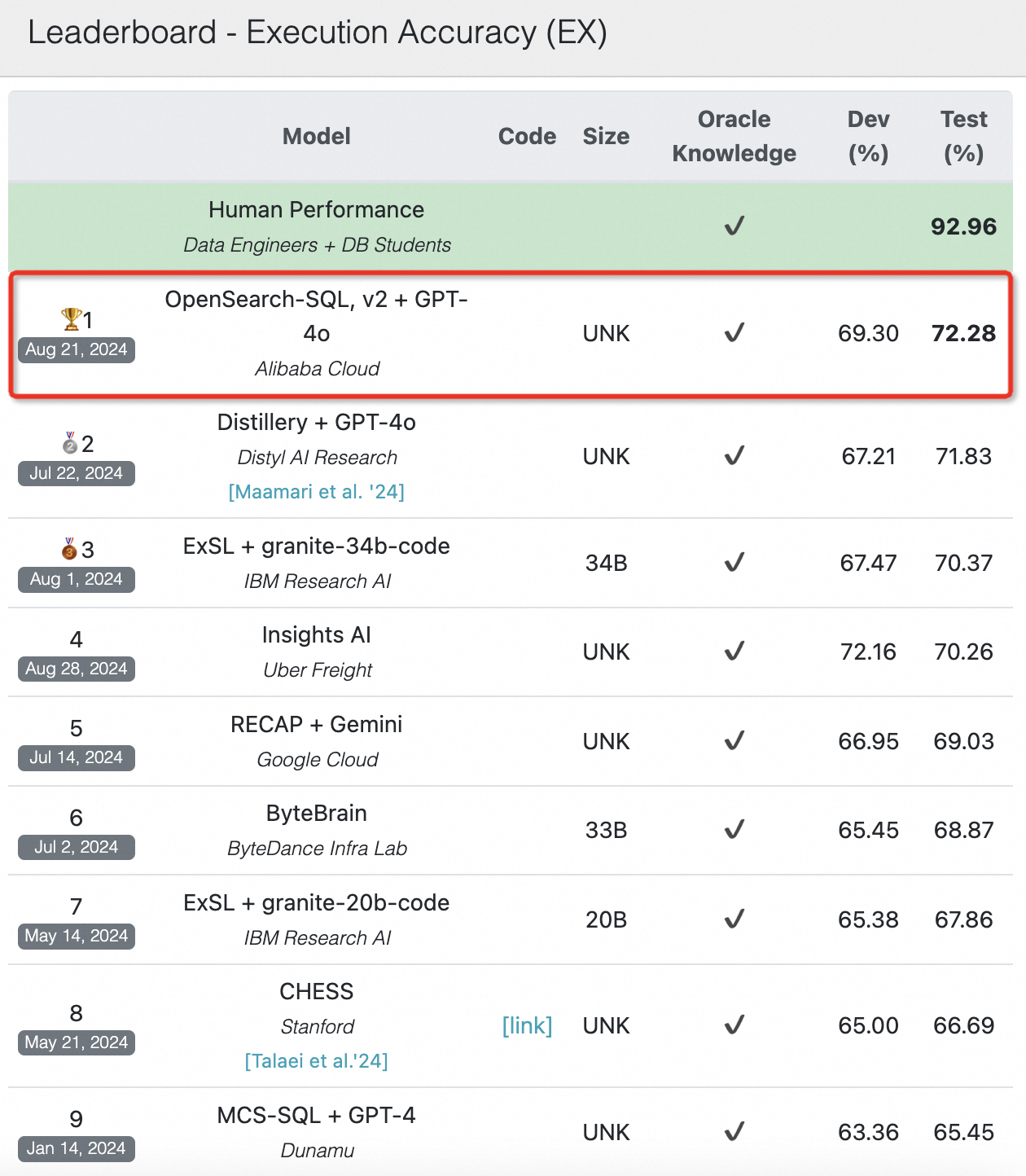
Text-to-SQL技术升级 - 阿里云OpenSearch-SQL在BIRD榜单夺冠方法
Text-to-SQL技术升级 - 阿里云OpenSearch-SQL在BIRD榜单夺冠方法 Text-to-SQL 任务旨在将自然语言查询转换为结构化查询语言(SQL),从而使非专业用户能够便捷地访问和操作数据库。近期,阿里云的 OpenSearch 引擎凭借其一致性对齐技术,在当前极具影响力的 Text-to-SQL 任务…...

[性能]高速收发的TCP/MQTT通信
Nagle算法是一种TCP/IP协议中的优化算法,旨在减少小数据包的数量,从而减少网络拥塞的可能性。该算法规定,在一个TCP连接上最多只能有一个未被确认的小分组。当数据被发送后,如果收到确认(ACK)之前&#x…...

OpenHarmony(鸿蒙南向开发)——标准系统方案之瑞芯微RK3568移植案例(下)
往期知识点记录: OpenHarmony(鸿蒙南向开发)——轻量系统STM32F407芯片移植案例 OpenHarmony(鸿蒙南向开发)——Combo解决方案之W800芯片移植案例 OpenHarmony(鸿蒙南向开发)——小型系统STM32M…...

网络安全学习(五)Burpsuite实战
bp功能确实强大,记录一个bp手机验证码的实例。 当然,首先要打开bp,设置好浏览器的代理。 浏览器访问实例网址www.xxx.com(隐藏真实网址)。 真实网址有个注册功能,需要手机验证码。 好的,我们…...

ego-planner开源代码之simulator.xml介绍分析
ego-planner开源代码之simulator.xml介绍&分析 1. 源由2. simulator配置2.1 配置入参2.2 mockamap_node 地图生成节点2.3 quadrotor_simulator_so3 四旋翼仿真节点2.4 Nodelet机制 四旋翼控制节点2.5 odom_visualization 里程计数据2.6 pcl_render_node 本地感知 3. 总结 1…...

论文阅读笔记 --- 图模互补:知识图谱与大模型融合综述 --- 按参考文献整理
Large Language Models’ Understanding of Math: Source Criticism and Extrapolation Submitted on 12 Nov 2023大模型在处理结构化推理方面(如解决数学问题[99])表现不佳 Tree of Thoughts: Deliberate Problem Solving with Large Language Models S…...

Cpp类和对象(上)(3)
文章目录 前言一、面向过程与面向对象初步认识二、类的引入三、类的定义四、类的访问限定符及类的封装类的访问限定符类的封装 五、类的作用域(类域)六、类的实例化七、类对象模型如何计算类对象的大小类对象的存储方式猜测 八、this指针this指针的引出this指针的特性 九、C语言…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
