当前位置： 首页 > news >正文

将硬盘的GPT 转化为MBR格式

news 2026/2/9 21:30:21

遇到的问题

在重新安装系统时，磁盘遇到无法空间分配给系统。

在这里插入图片描述

解决方式

使用Windows10镜像 U盘安装，选择磁盘时，转换磁盘格式为MBR。然后退出安装程序。

Shift + F10# 输入
diskpart# 查看磁盘信息
list disk# 选择需要转换的磁盘，例如 磁盘0
select disk 0# 输入clear来清理磁盘分区
clear# 输入convert mbr 来转换为MBR分区
convert mbr# 退出命令提示符，继续安装系统

相关文章：

将硬盘的GPT 转化为MBR格式

遇到的问题 在重新安装系统时，磁盘遇到无法空间分配给系统。 解决方式 使用Windows10镜像 U盘安装，选择磁盘时，转换磁盘格式为MBR。然后退出安装程序。 Shift F10# 输入 diskpart# 查看磁盘信息 list disk# 选择需要转换的磁盘&#xff0…...

编程日记 2024/9/18 16:53:03

C++基于select和epoll的TCP服务器

select版本 服务器 #include <arpa/inet.h> #include <stdlib.h> #include <stdio.h> #include <string.h> #include <unistd.h> #include <sys/socket.h> #include <string> #include <pthread.h> #include <sys/select…...

编程日记 2024/9/18 16:50:55

SpringBoot 读取配置文件的4种方式

文章目录 1. Value 注解读取单个属性2. 使用 ConfigurationProperties 注解3. 通过 Environment 对象读取属性4. 使用 PropertySource 注解加载额外的配置文件 在 Spring Boot 中&#xff0c;application.yml 文件用于配置应用程序的属性&#xff0c;Spring Boot 默认会从 src/…...

编程日记 2024/9/18 16:48:50

【车载开发系列】ParaSoft单元测试环境配置（三）

【车载开发系列】ParaSoft单元测试环境配置（三） 【车载开发系列】ParaSoft单元测试环境配置（三） 【车载开发系列】ParaSoft单元测试环境配置（三）一. 去插桩设置Step1：静态解析代码Step2：编辑Parasoft文件Step3：确认去插桩二. 新增测试用例Step1：生成测试用例Step2：执…...

编程日记 2024/9/18 16:47:43

如何让Threejs的canvas背景透明？

在Three.js中&#xff0c;要让Canvas的背景透明&#xff0c;只显示场景中的模型或物体&#xff0c;有两个关键点&#xff1a; 一、对渲染器&#xff08;Renderer&#xff09;进行alpha为true配置&#xff1b; 二、通过CSS设置&#xff0c;使canvas设定为透明背景模式。 以下是代…...

编程日记 2024/9/18 16:46:38

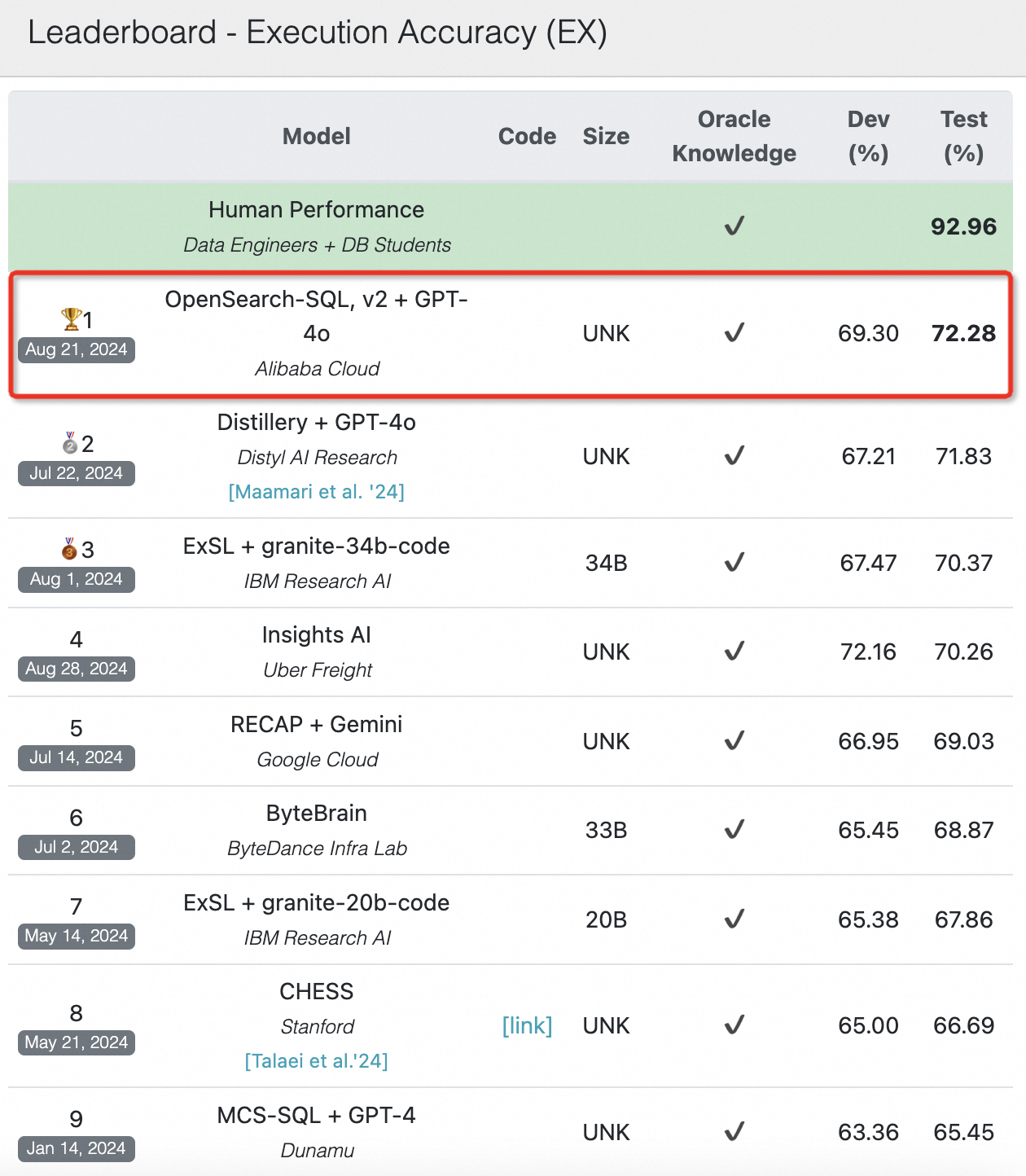
Text-to-SQL技术升级 - 阿里云OpenSearch-SQL在BIRD榜单夺冠方法

Text-to-SQL技术升级 - 阿里云OpenSearch-SQL在BIRD榜单夺冠方法 Text-to-SQL 任务旨在将自然语言查询转换为结构化查询语言（SQL），从而使非专业用户能够便捷地访问和操作数据库。近期，阿里云的 OpenSearch 引擎凭借其一致性对齐技术，在当前极具影响力的 Text-to-SQL 任务…...

编程日记 2024/9/18 16:44:28

[性能]高速收发的TCP/MQTT通信

Nagle算法‌是一种TCP/IP协议中的优化算法&#xff0c;旨在减少小数据包的数量&#xff0c;从而减少网络拥塞的可能性。该算法规定&#xff0c;在一个TCP连接上最多只能有一个未被确认的小分组。当数据被发送后&#xff0c;如果收到确认&#xff08;ACK&#xff09;之前&#x…...

编程日记 2024/9/18 16:43:25

OpenHarmony（鸿蒙南向开发）——标准系统方案之瑞芯微RK3568移植案例(下)

往期知识点记录&#xff1a; OpenHarmony&#xff08;鸿蒙南向开发&#xff09;——轻量系统STM32F407芯片移植案例 OpenHarmony&#xff08;鸿蒙南向开发&#xff09;——Combo解决方案之W800芯片移植案例 OpenHarmony&#xff08;鸿蒙南向开发&#xff09;——小型系统STM32M…...

编程日记 2024/9/18 16:40:13

网络安全学习（五）Burpsuite实战

bp功能确实强大&#xff0c;记录一个bp手机验证码的实例。 当然&#xff0c;首先要打开bp&#xff0c;设置好浏览器的代理。 浏览器访问实例网址www.xxx.com&#xff08;隐藏真实网址&#xff09;。 真实网址有个注册功能&#xff0c;需要手机验证码。 好的&#xff0c;我们…...

编程日记 2024/9/18 16:37:58

ego-planner开源代码之simulator.xml介绍分析

ego-planner开源代码之simulator.xml介绍&分析 1. 源由2. simulator配置2.1 配置入参2.2 mockamap_node 地图生成节点2.3 quadrotor_simulator_so3 四旋翼仿真节点2.4 Nodelet机制 四旋翼控制节点2.5 odom_visualization 里程计数据2.6 pcl_render_node 本地感知 3. 总结 1…...

编程日记 2024/9/18 16:33:47

论文阅读笔记 --- 图模互补：知识图谱与大模型融合综述 --- 按参考文献整理

Large Language Models’ Understanding of Math: Source Criticism and Extrapolation Submitted on 12 Nov 2023大模型在处理结构化推理方面&#xff08;如解决数学问题[99]&#xff09;表现不佳 Tree of Thoughts: Deliberate Problem Solving with Large Language Models S…...

编程日记 2024/9/18 16:26:26

Cpp类和对象(上)(3)

文章目录 前言一、面向过程与面向对象初步认识二、类的引入三、类的定义四、类的访问限定符及类的封装类的访问限定符类的封装 五、类的作用域(类域)六、类的实例化七、类对象模型如何计算类对象的大小类对象的存储方式猜测 八、this指针this指针的引出this指针的特性 九、C语言…...

编程日记 2024/9/18 16:21:38

【微信小程序】连续拍照功能实现

前言&#xff1a; 最近在使用uniapp开发微信小程序&#xff0c;遇到这样一个需求&#xff0c;用户想要连续拍照&#xff0c;拍完之后可以删除照片&#xff0c;保留自己想要的照片&#xff0c;然后上传到服务器上。由于原生的方法只能一个个拍照上传&#xff0c;所以只能自己通过…...

编程日记 2024/9/18 16:18:26

JavaSE:11、内部类

学习 资源1 学习资源 2 1、成员内部类 import com.test.*;public class Main {public static void main(String [] argv){Person personnew Person();//Person构造函数Person.Woman womanperson.new Woman();//woman构造函数} }package com.test;public class Person {publ…...

编程日记 2024/9/18 16:17:25

VTD激光雷达（7）——07_OptiX_Variables_Advanced

文章目录 前言一、总结 前言 一、 1 和上图蓝绿的区别在于 总结...

编程日记 2024/9/18 16:15:22

运维工程师面试整理-自动化运维

自动化运维是现代运维工作中不可或缺的一部分，它可以大幅提升效率，减少人为错误，并使得大规模环境管理变得可行。在面试中，面试官通常会通过自动化运维相关的问题来评估你在自动化工具使用、脚本编写、CI/CD 实践以及系统监控等方面的能力。以下是关于自动化运维的详细内容…...

编程日记 2024/9/18 16:14:17

【JAVA基础】实现Tomcat基本功能

文章目录 TCP/IP协议Socket编程ServletTomcat 在搜索了两三天之后&#xff0c;也是大概弄懂了Tomcat是个什么东西&#xff0c;我们在说Tomcat之前&#xff0c;先来了解一下下面这三个东西&#xff1a; TCP/IP协议 TCP/IP 是互联网通信的基础协议。TCP&#xff08;传输控制协议…...

编程日记 2024/9/18 16:12:11

风力发电叶片缺陷检测数据集

风力发电叶片缺陷检测数据集】nc: 4 names: [Burn Mark, Coating_defects, Crack, EROSION ] 名称&#xff1a;【烧伤痕迹, 涂层缺陷, 裂缝&#xff0c;侵蚀】共1095张&#xff0c;8:1:1比例划分&#xff0c;&#xff08;train;876张&#xff0c;val&#xff1a;109张&#xff…...

编程日记 2024/9/18 16:11:10

数据类型自动转换的解决方案

数据类型自动转换的解决方案 java8、jdk8背景 为方便测试框架数据处理以及方便查看一些数据&#xff0c;弄了一个工具类&#xff0c;部分要点简要说明。 主要涉及到字符串与其他类型的相互转换&#xff0c;无其他类型之间的相互转换。 轻量测试框架实现与使用的总篇可见此文…...

编程日记 2024/9/18 16:10:05

大厂校招：唯品会Java面试题及参考答案

SortedSet 的原理 SortedSet 是一个有序的集合接口，它继承自 Set 接口。在 Java 中，常见的实现类有 TreeSet。 TreeSet 实现了 SortedSet 接口，它使用红黑树来维护集合中元素的有序性。红黑树是一种自平衡的二叉搜索树，具有以下特点： 每个节点要么是红色，要么是黑色。根节…...

编程日记 2024/9/18 16:08:56

浅谈 React Hooks

React Hooks 是 React 16.8 引入的一组 API&#xff0c;用于在函数组件中使用 state 和其他 React 特性&#xff08;例如生命周期方法、context 等&#xff09;。Hooks 通过简洁的函数接口&#xff0c;解决了状态与 UI 的高度解耦&#xff0c;通过函数式编程范式实现更灵活 Rea…...

编程新知 2025/9/23 15:13:40

龙虎榜——20250610

上证指数放量收阴线&#xff0c;个股多数下跌&#xff0c;盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型&#xff0c;指数短线有调整的需求&#xff0c;大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的&#xff1a;御银股份、雄帝科技 驱动…...

编程新知 2026/2/8 15:03:06

【磁盘】每天掌握一个Linux命令 - iostat

目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat&#xff08;I/O Statistics&#xff09;是Linux系统下用于监视系统输入输出设备和CPU使…...

编程新知 2025/9/30 16:39:11

DIY｜Mac 搭建 ESP-IDF 开发环境及编译小智 AI

前一阵子在百度 AI 开发者大会上&#xff0c;看到基于小智 AI DIY 玩具的演示&#xff0c;感觉有点意思&#xff0c;想着自己也来试试。 如果只是想烧录现成的固件&#xff0c;乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外&#xff0c;还提供了基于网页版的 ESP LA…...

编程新知 2026/2/3 8:13:35

汇编常见指令

汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX&#xff08;不访问内存&#xff09;XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

编程新知 2026/1/23 2:04:44

html css js网页制作成品——HTML+CSS榴莲商城网页设计（4页）附源码

目录 一、&#x1f468;‍&#x1f393;网站题目 二、✍️网站描述 三、&#x1f4da;网站介绍 四、&#x1f310;网站效果 五、&#x1fa93; 代码实现 &#x1f9f1;HTML 六、&#x1f947; 如何让学习不再盲目 七、&#x1f381;更多干货 一、&#x1f468;‍&#x1f…...

编程新知 2026/2/7 22:17:30

Git 3天2K星标：Datawhale 的 Happy-LLM 项目介绍（附教程）

引言 在人工智能飞速发展的今天&#xff0c;大语言模型&#xff08;Large Language Models, LLMs&#xff09;已成为技术领域的焦点。从智能写作到代码生成&#xff0c;LLM 的应用场景不断扩展&#xff0c;深刻改变了我们的工作和生活方式。然而&#xff0c;理解这些模型的内部…...

编程新知 2026/1/29 11:06:33

elementUI点击浏览table所选行数据查看文档

项目场景&#xff1a; table按照要求特定的数据变成按钮可以点击 解决方案&#xff1a; <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

编程新知 2026/2/4 18:42:53

高考志愿填报管理系统---开发介绍

高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发&#xff0c;采用现代化的Web技术&#xff0c;为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## &#x1f4cb; 系统概述 ### &#x1f3af; 系统定…...

编程新知 2026/1/23 4:26:12

​​企业大模型服务合规指南：深度解析备案与登记制度​​

伴随AI技术的爆炸式发展&#xff0c;尤其是大模型&#xff08;LLM&#xff09;在各行各业的深度应用和整合&#xff0c;企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者&#xff0c;还是积极拥抱AI转型的传统企业&#xff0c;在面向公众…...

编程新知 2026/2/9 1:32:22