力扣3014.输入单词需要的最少按键次数I
给你一个字符串 word,由 不同 小写英文字母组成。
电话键盘上的按键与 不同 小写英文字母集合相映射,可以通过按压按键来组成单词。例如,按键 2 对应 ["a","b","c"],我们需要按一次键来输入 "a",按两次键来输入 "b",按三次键来输入 "c"。
现在允许你将编号为 2 到 9 的按键重新映射到 不同 字母集合。每个按键可以映射到 任意数量 的字母,但每个字母 必须 恰好 映射到 一个 按键上。你需要找到输入字符串 word 所需的 最少 按键次数。
返回重新映射按键后输入 word 所需的 最少 按键次数。
下面给出了一种电话键盘上字母到按键的映射作为示例。注意 1,*,# 和 0 不 对应任何字母。
示例 1:
输入:word = "abcde" 输出:5 解释:图片中给出的重新映射方案的输入成本最小。 "a" -> 在按键 2 上按一次 "b" -> 在按键 3 上按一次 "c" -> 在按键 4 上按一次 "d" -> 在按键 5 上按一次 "e" -> 在按键 6 上按一次 总成本为 1 + 1 + 1 + 1 + 1 = 5 。 可以证明不存在其他成本更低的映射方案。
示例 2:
输入:word = "xycdefghij" 输出:12 解释:图片中给出的重新映射方案的输入成本最小。 "x" -> 在按键 2 上按一次 "y" -> 在按键 2 上按两次 "c" -> 在按键 3 上按一次 "d" -> 在按键 3 上按两次 "e" -> 在按键 4 上按一次 "f" -> 在按键 5 上按一次 "g" -> 在按键 6 上按一次 "h" -> 在按键 7 上按一次 "i" -> 在按键 8 上按一次 "j" -> 在按键 9 上按一次 总成本为 1 + 2 + 1 + 2 + 1 + 1 + 1 + 1 + 1 + 1 = 12 。 可以证明不存在其他成本更低的映射方案。
题解:
class Solution:def minimumPushes(self, word: str) -> int:a, b = divmod(len(word), 8)return ((a << 2) + b) * (a + 1)class Solution:def minimumPushes(self, word: str) -> int:n = len(word)keys = 8 # 按键数量,从2到9total = 0position = 1 # 当前按键位置,从1开始remaining = nwhile remaining > 0:# 每一层最多可以分配到8个字母assign = min(keys, remaining)total += assign * positionremaining -= assignposition += 1return total
解题思路
为了最小化总按键次数,我们应尽可能将更多的字母分配到各按键的前几个位置。具体步骤如下:
确定按键数量:
- 有
8个按键(编号2到9)。分配字母到按键的位置:
- 首先,尽可能多地将字母分配到每个按键的第一个位置(每个按键最多一个字母,成本为
1)。- 如果字母数量超过
8,则将剩余的字母分配到按键的第二个位置(每个按键最多一个字母,成本为2)。- 依此类推,直到所有字母都被分配。
计算总成本:
- 对于每一层(即每个按键的位置),计算分配到该层的字母数量与其对应的成本,然后累加。
实现步骤
初始化变量:
n:字符串word的长度。keys:按键的数量,即8。total:总成本,初始为0。position:当前分配的按键位置,初始为1。remaining:剩余未分配的字母数量,初始为n。循环分配字母:
- 在每一层(按键位置)中,分配尽可能多的字母(最多
8个)。- 计算分配到当前层的字母数量
assign,即min(keys, remaining)。- 更新总成本:
total += assign * position。- 减少剩余字母数量:
remaining -= assign。- 移动到下一层:
position += 1。返回结果:
- 循环结束后,返回
total作为最小按键总成本。代码说明
函数
minimumPushes:
- 接受一个字符串
word。- 计算并返回重新映射后输入该
word所需的最少按键次数。- 使用贪心策略,优先将字母分配到每个按键的前几个位置,以降低总成本。
变量解释:
n:字符串word的长度。keys:按键数量(编号2到9共8个)。total:总按键次数。position:当前分配的按键位置(第几次按键)。remaining:剩余未分配的字母数量。逻辑流程:
- 在每一层(按键位置)中,尽可能多地分配字母(最多
8个)。- 更新总成本,并减少剩余字母数量。
- 重复上述过程,直到所有字母都被分配。
相关文章:

力扣3014.输入单词需要的最少按键次数I
给你一个字符串 word,由 不同 小写英文字母组成。 电话键盘上的按键与 不同 小写英文字母集合相映射,可以通过按压按键来组成单词。例如,按键 2 对应 ["a","b","c"],我们需要按一次键来输入 "…...

【Git】远程仓库
本博客的环境是 Ubuntu/Linux 文章目录 集中式与分布式的区别远程仓库新建远程仓库克隆远程仓库向远程仓库推送从远程仓库拉取 配置Git忽略指定文件给命令配置别名 标签管理创建标签操作标签 多人协作本地分支与远程分支连接场景一场景二 集中式与分布式的区别 引荐自关于Git这…...

苹果手机铃声怎么设置自己的歌?3个方法自定义手机铃声
苹果手机内部的手机铃声库只有固定的几首铃声,且都是纯音乐,比较单调,并不是所有用户都喜欢这些铃声。那么,苹果手机铃声怎么设置自己的歌呢?小编这里有3个方法,可以教大家如何将手机铃声设置成自己喜欢的歌…...
828华为云征文|华为Flexus云服务器搭建Cloudreve私人网盘
一、华为云 Flexus X 实例:开启高效云服务新篇🌟 在云计算的广阔领域中,资源的灵活配置与卓越性能犹如璀璨星辰般闪耀。华为云 Flexus X 实例恰似一颗最为耀眼的新星,将云服务器技术推向了崭新的高度。 华为云 Flexus X 实例基于…...

【AI学习】AI绘画发展简史
无意中读了一篇发表自2022年的文章,《AI绘画何以突飞猛进? 从历史到技术突破, 一文读懂火爆的AI绘画发展史》,写的比较有意思,科普了好多我原来不知道的历史。 简单提炼一下,做个笔记。 AI绘画重要事件 2012年 Google两位大名…...

使用LangChain创建简单的语言模型应用程序【快速入门指南】
## 引言在这篇文章中,我们将展示如何使用LangChain构建一个简单的语言模型(LLM)应用程序。这个应用程序的功能是将文本从英语翻译成其他语言。尽管应用程序的逻辑相对简单,但它能够帮助我们学习如何使用LangChain进行更多复杂的功…...
嵌入式人工智能项目及人工智能应用项目——大合集列表查阅
本文的项目合集列表可能更新不及时(会及时更新),可查阅实时更新的链接如下。 嵌入式人工智能及人工智能应用项目合集实时更新链接如下: 阿齐嵌入式人工智能及人工智能应用项目合集 (kdocs.cn)https://www.kdocs.cn/l/cc97tuieys4…...

心觉:成功学就像一把刀,有什么作用关键在于使用者(一)
Hi,我是心觉,与你一起玩转潜意识、脑波音乐和吸引力法则,轻松掌控自己的人生! 挑战每日一省写作173/1000天 很多人觉得成功学是鸡汤,是没用的,甚至是骗人的 我先保持中立,不知道对不对 我们先…...
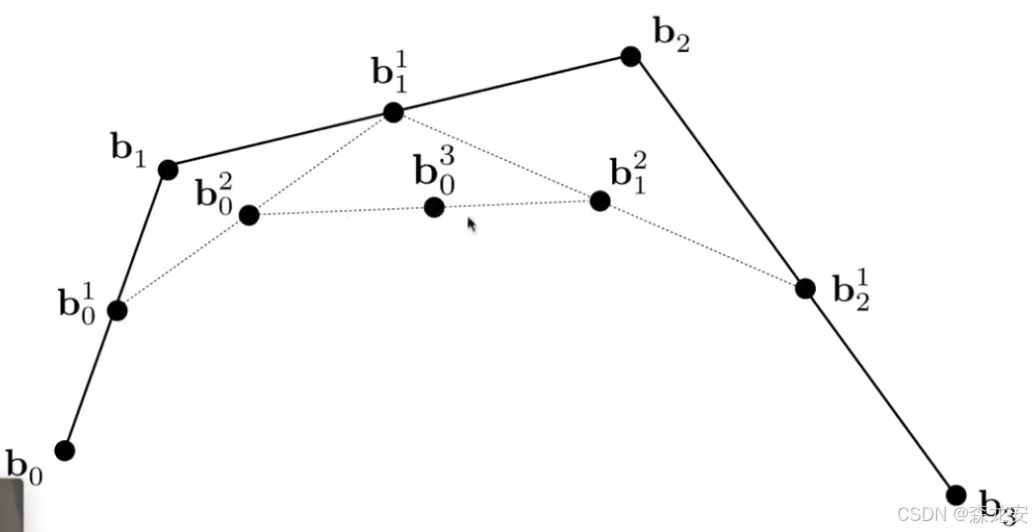
GAMES101(10节,几何)
Geometry implicit隐式几何表示: 函数f(x,y,z): 根据函数fn描述几何,遍历所有空间内 的点,如果带入xyz到函数f(x,y,z)结果0那就绘制这个点 如果xyz求值结果>0表示在几何外,0在表面,<0在几何内 构造几何csg(…...

Android 中音频焦点的使用场景及示例
Android 中音频焦点的使用场景及代码示例 一、音频焦点简介 在 Android 系统中,音频焦点(Audio Focus)是一种机制,用于管理多个应用程序同时播放音频时的冲突。当一个应用程序请求音频焦点并获得它时,其他应用程序在…...

2. JDBC驱动是什么?如何在Java项目中配置MySQL的JDBC驱动?
JDBC驱动 是一种软件组件,它使Java应用程序能够与数据库进行交互。JDBC驱动是JDBC API的实现,负责将Java程序中的标准JDBC方法调用转化为数据库特定的操作。每个数据库(如MySQL、PostgreSQL、Oracle等)都有对应的JDBC驱动程序&…...

Nginx 跨域 + 无法设置 Cookie 解决办法
今天来分享一下关于项目部署上线时怎么解决跨域问题!!! 首先感谢一下大佬的方法,才让这个困扰我很久的问题得以解决!!! 这也是我请教大佬才解决的问题,大佬和我说,这是他耗费两周才解决的问题,我这也是属于前人栽树后人乘凉了,嘿嘿嘿!!! 前端问题 前端没有携带 cookie 导致后端…...
北森笔试测评之言语理解到底难不难
前篇笔记我提到过,言语理解是最难的,有同学质疑了。言语我都会做呀,甚至有的可以搜到,而图标和图形我有的不会。这里需要指出,会做不等于作对,可以回顾到高中甚至初中的时候,感觉做的好的一般都…...

Ubuntu下beanstalkd无法绑定局域网IP地址以及消息队列beanstalkd上的error: JOB_TOO_BIG的解决
一、ubuntu下beanstalkd无法绑定局域网IP地址 今天因为业务需要,我把之前安装的beanstalkd所绑定的IP地址由127.0.0.1改成局域网IP地址,但是怪了,显示beanstalkd已经启动,查看端口监控也显示IP地址变了,但是使用telnet…...
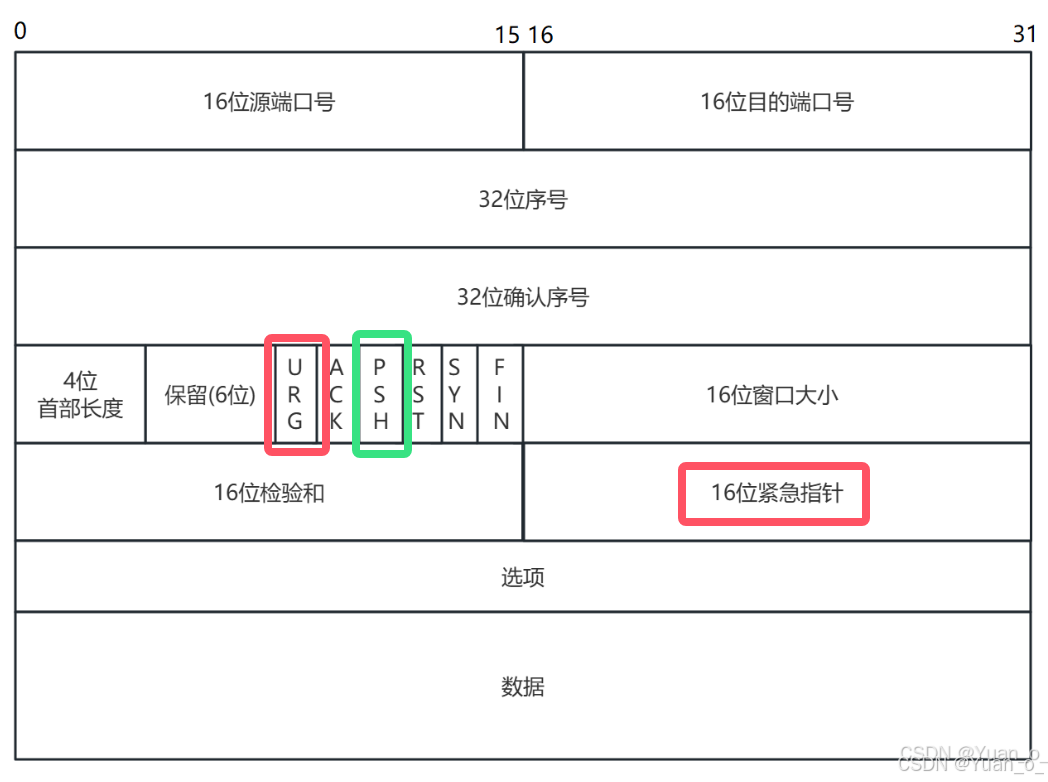
网络原理(3)—— 应用层、传输层(TCP)
1. 应用层 日常开发中最常用到的一层,主要涉及到两种情况: 1) 使用现成的应用层协议 2) 自己定义应用层协议 1.1 自定义应用层协议的流程 1. 明确前后端交互过程中需要传递哪些信息 实例:开发一个外卖软件 打开软件,首先需要展…...

Flutter - Win32程序是如何执行main函数
Win32程序的主体结构 int APIENTRY wWinMain(_In_ HINSTANCE instance, _In_opt_ HINSTANCE prev,_In_ wchar_t *command_line, _In_ int show_command) {// Attach to console when present (e.g., flutter run) or create a// new console when running with a debugger.if …...

linux-系统管理与监控-日志管理
Linux 系统管理与监控:日志管理 1. 日志管理概述 日志文件是系统在运行过程中记录的各种信息,它们是系统管理员排查问题、监控系统健康状况的重要工具。在 Linux 系统中,日志涵盖了系统事件、内核信息、用户操作、软件服务和应用程序等内容…...
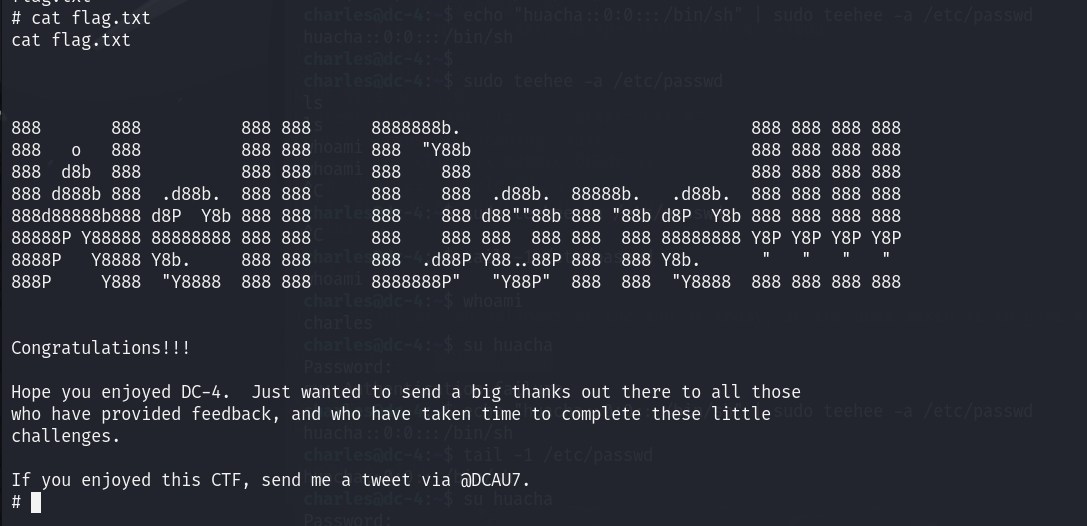
VulhubDC-4靶机详解
项目地址 https://download.vulnhub.com/dc/DC-4.zip实验过程 将下载好的靶机导入到VMware中,设置网络模式为NAT模式,然后开启靶机虚拟机 使用nmap进行主机发现,获取靶机IP地址 nmap 192.168.47.1-254根据对比可知DC-4的一个ip地址为192.1…...
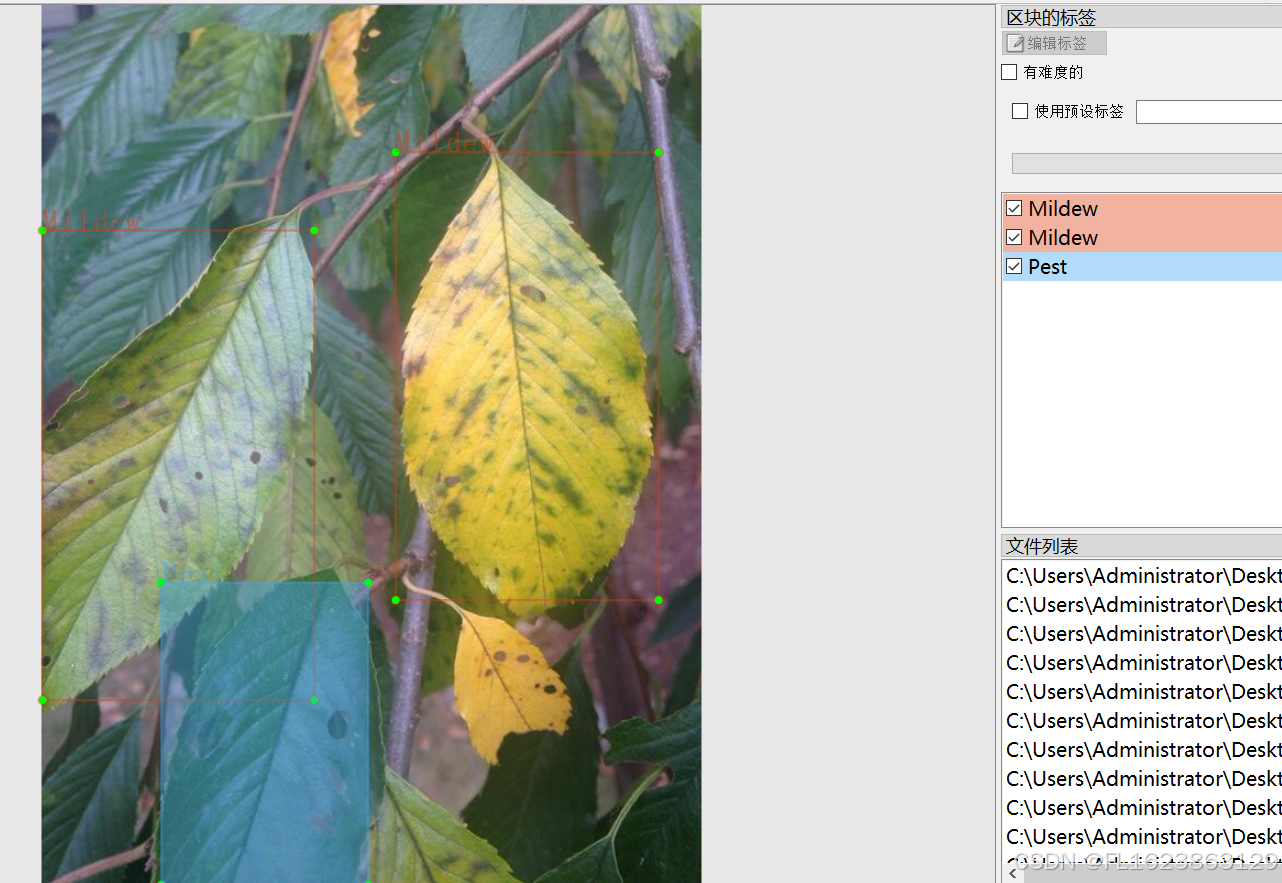
[数据集][目标检测]烟叶病害检测数据集VOC+YOLO格式612张3类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):612 标注数量(xml文件个数):612 标注数量(txt文件个数):612 标注类别…...

Sapiens——人类视觉大模型的基础
引言 大规模预训练以及随后针对特定任务的语言建模微调取得了显著成功,已将这种方法确立为标准做法。同样, 计算机视觉方法正逐步采用大规模数据进行预训练。LAION5B、Instagram-3.5B、JFT-300M、LVD142M、Visual Genome 和 YFCC100M 等大型数据集的出现…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
