Meta-Learning数学原理

🍃作者介绍：双非本科大四网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发，目前开始人工智能领域相关知识的学习
🦅个人主页：@逐梦苍穹
📕所属专栏：人工智能
🌻gitee地址：xzl的人工智能代码仓库
✈ 您的一键三连，是我创作的最大动力🌹

之前介绍过元学习的内容：https://xzl-tech.blog.csdn.net/article/details/142025393
这篇文章讲一下Meta-Learning的数学原理。

什么是元学习

元学习（Meta-Learning），也称为“学习如何学习”，是一种机器学习方法，其目的是通过学习算法的经验和结构特性，提升算法在新任务上的学习效率。

换句话说，元学习试图学习一种更有效的学习方法，使得模型能够快速适应新的任务或环境。

---

传统的机器学习算法通常需要大量的数据来训练模型，并且当数据分布发生变化或者遇到一个新任务时，模型往往需要重新训练才能保持良好的性能。

而元学习则不同，它通过 从多个相关任务中学习，从而在面对新任务时更快速地进行学习。

元学习的核心思想是利用“学习的经验”来提高学习的速度和质量。

在元学习的框架中，有两个层次的学习过程：

1. 元学习者（Meta-Learner）： 负责从多个任务中提取经验和知识，用于更新学习策略或模型参数。
2. 基础学习者（Base Learner）： 在每个具体任务上执行实际的学习过程。

元学习的目标

元学习的目标是解决以下问题：

• 快速适应： 当模型面临新任务时，能够基于已有的经验快速适应，而无需大量的数据和计算资源。
• 跨任务泛化： 提高模型从多个任务中学习到的知识在新任务上的泛化能力。
• 提高数据效率： 减少模型在新任务上所需的数据量，尤其是在数据稀缺或高昂的情况下。

元学习的类型

元学习可以按照不同的方式分类，以下是三种主要类型：

1. 基于模型的元学习（Model-Based Meta-Learning）：
   • 这种方法通过直接设计一种能够快速适应新任务的模型架构，通常是通过某种特殊的神经网络结构来实现的。例如，基于记忆的神经网络（如 LSTM 或 Memory-Augmented Neural Networks）被设计成能有效地记住过去的任务信息，并在新任务上进行快速调整。
   • 例子： MANN（Memory-Augmented Neural Networks），SNAIL（Simple Neural Attentive Meta-Learner）。
2. 基于优化的元学习（Optimization-Based Meta-Learning）：
   • 这种方法的核心是通过改进优化过程本身来实现快速学习。其代表算法是 MAML（Model-Agnostic Meta-Learning），它通过在所有任务上共享一个初始模型参数，使得初始模型在每个任务上进行少量梯度下降更新后能够快速适应新任务。
   • 例子： MAML（Model-Agnostic Meta-Learning），Reptile。
3. 基于记忆的元学习（Memory-Based Meta-Learning）：
   • 这类方法直接存储并检索训练过程中的经验数据。当遇到新任务时，通过查找与之相似的旧任务，并利用这些旧任务的数据和经验来快速学习。k-NN（k-近邻）方法是最基本的例子，而更复杂的方法可能使用深度记忆网络。
   • 例子： Meta Networks，Prototypical Networks。

数学推导

1. 传统机器学习的数学表述

在传统的机器学习中，我们通常试图找到一个函数$f_{\theta }$来最小化给定数据集$D$的损失函数：
${\theta }^{\ast }=\arg {\min }_{\theta }L(f_{\theta },D)$
其中：

• $\theta$是模型的参数。
• $L(f_{\theta },D)$是损失函数，例如交叉熵损失。
• 通过梯度下降等优化方法，我们不断更新参数$\theta$以最小化损失。

2. 元学习的基本思想

元学习的目标是找到一种元算法$F_{\varphi }$，使得它可以快速学习新任务。这里的关键是学习一种 学习算法。换句话说，元学习希望找到一组元参数$\varphi$，从而在给定一个新任务$T_i$时，使用少量数据和梯度更新就可以迅速找到特定任务的参数${\theta }_i$。

3. MAML 算法推导

MAML 的目标是学习一个初始模型参数$\theta$，使得它可以通过少量的梯度更新快速适应新任务。

3.1 元任务设置

假设有一组任务 { T 1 , T 2 , … , T N } \{T_1, T_2, \dots, T_N\} {T1​,T2​,…,TN​}，每个任务$T_i$有自己的训练数据$D_i^{\text{train}}$和测试数据$D_i^{\text{test}}$。

3.2 内层优化：任务级别学习

对于每个任务$T_i$，我们首先使用任务的训练数据$D_i^{\text{train}}$和当前的模型参数$\theta$进行一次或多次梯度更新，得到任务特定的参数${\theta }_i^{\prime }$：
${\theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})$
其中：

• $\alpha$是学习率。
• $L_{T_i}(f_{\theta },D_i^{\text{train}})$是任务$T_i$的损失函数，例如对于分类任务可以是交叉熵损失。

3.3 外层优化：元级别学习

在每个任务的测试数据上评估更新后的模型参数${\theta }_i^{\prime }$，计算其损失，并在所有任务上最小化测试损失的总和：
${\min }_{\theta }{\sum }_{i=1}^N{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})$
将${\theta }_i^{\prime }$展开，这个目标实际上是关于初始参数$\theta$的优化问题：
${\min }_{\theta }{\sum }_{i=1}^N{L}_{T_i}(f_{\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})},D_i^{\text{test}})$

3.4 元梯度计算

为了优化这个目标，我们需要对$\theta$求梯度。这里涉及二阶梯度，因为${\theta }_i^{\prime }$是通过内层优化得到的：
$\theta \leftarrow \theta -\beta {\sum }_{i=1}^N{\nabla }_{\theta }{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})$
其中$\beta$是元学习的学习率。

• 这个更新包含了二阶导数项：${\nabla }_{\theta }{\theta }_i^{\prime }={\nabla }_{\theta }\left(\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})\right)$。

3.5 最终更新规则

最终的元学习更新规则可以写为：
$\theta \leftarrow \theta -\beta {\sum }_{i=1}^N{\nabla }_{\theta }{L}_{T_i}\left(f_{\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})},D_i^{\text{test}}\right)$

4. 算法合并

将内层优化${\theta }_i^{\prime }$代入外层优化的公式中，外层优化的梯度${\nabla }_{\theta }{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})$需要应用链式法则：
$${\nabla }_{\theta }{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})={\nabla }_{\theta }{L}_{T_i}\left(f_{\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})},D_i^{\text{test}}\right)$$
通过链式法则，展开这个公式：
$${\nabla }_{\theta }{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})={\nabla }_{{\theta }_i^{\prime }}{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})\cdot {\nabla }_{\theta }{\theta }_i^{\prime }$$
其中${\nabla }_{\theta }{\theta }_i^{\prime }$的形式为：
$${\nabla }_{\theta }{\theta }_i^{\prime }=I-\alpha {\nabla }_{\theta }^2{L}_{T_i}(f_{\theta },D_i^{\text{train}})$$
$I$是单位矩阵，${\nabla }_{\theta }^2{L}_{T_i}(f_{\theta },D_i^{\text{train}})$是损失函数关于$\theta$的二阶导数（Hessian 矩阵）。

---

最终的公式：

将这些部分合并在一起，得到 MAML 的最终更新公式为：
$$\theta \leftarrow \theta -\beta \sum _{i=1}^N{\nabla }_{{\theta }_i^{\prime }}{L}_{T_i}\left(f_{\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})},D_i^{\text{test}}\right)\cdot \left(I-\alpha {\nabla }_{\theta }^2{L}_{T_i}(f_{\theta },D_i^{\text{train}})\right)$$

---

解释：

• 内层优化：第一部分${\theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{L}_{T_i}(f_{\theta },D_i^{\text{train}})$表示在每个任务上用梯度下降更新$\theta$，得到特定于任务的参数${\theta }_i^{\prime }$。
• 外层优化：外层优化考虑测试集上的损失，并通过链式法则计算对$\theta$的梯度。这部分的关键是包含了内层更新的二阶导数${\nabla }_{\theta }{\theta }_i^{\prime }$。
• 合并公式：最终的更新公式同时结合了内层和外层优化的过程，充分考虑了内层更新对外层优化的影响。

---

简化（在某些情况下）：

在实际应用中，计算二阶导数（Hessian 矩阵）非常昂贵。因此，有时会使用近似方法来简化计算，例如“一次近似 MAML (First-Order MAML, FOMAML)”，忽略二阶项，仅使用一阶导数进行更新。简化后的更新公式为：
$$\theta \leftarrow \theta -\beta \sum _{i=1}^N{\nabla }_{{\theta }_i^{\prime }}{L}_{T_i}(f_{{\theta }_i^{\prime }},D_i^{\text{test}})$$

这个简化版本去除了${\nabla }_{\theta }{\theta }_i^{\prime }$中的二阶导数计算。

5. 理解 MAML 的优化

通过上面的推导，MAML 的优化分为两个阶段：

1. 内层优化：在每个任务上利用任务的训练数据对模型进行一次或多次更新，以获得任务特定的模型参数。
2. 外层优化：在所有任务的测试数据上评估内层优化后的模型，并利用这个评估结果更新模型的初始参数。

图例

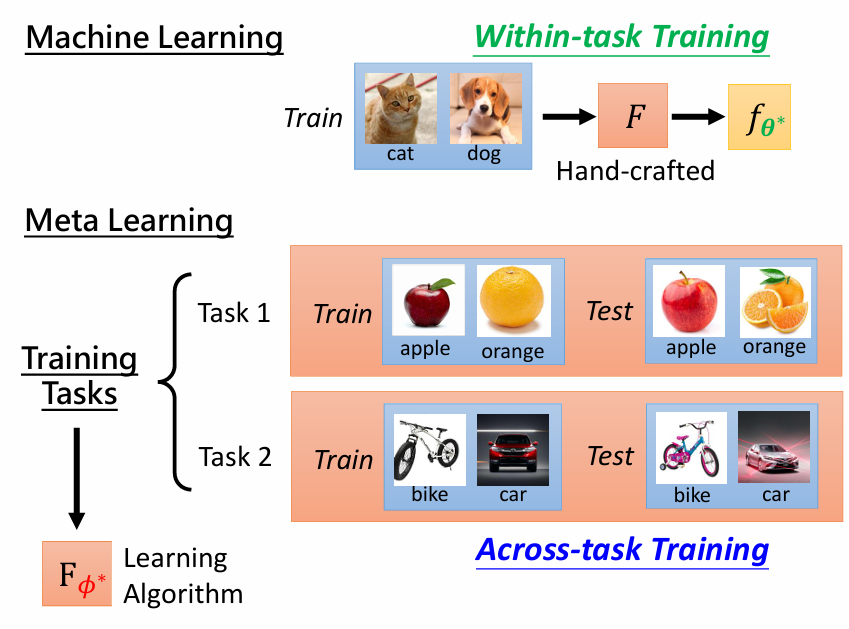
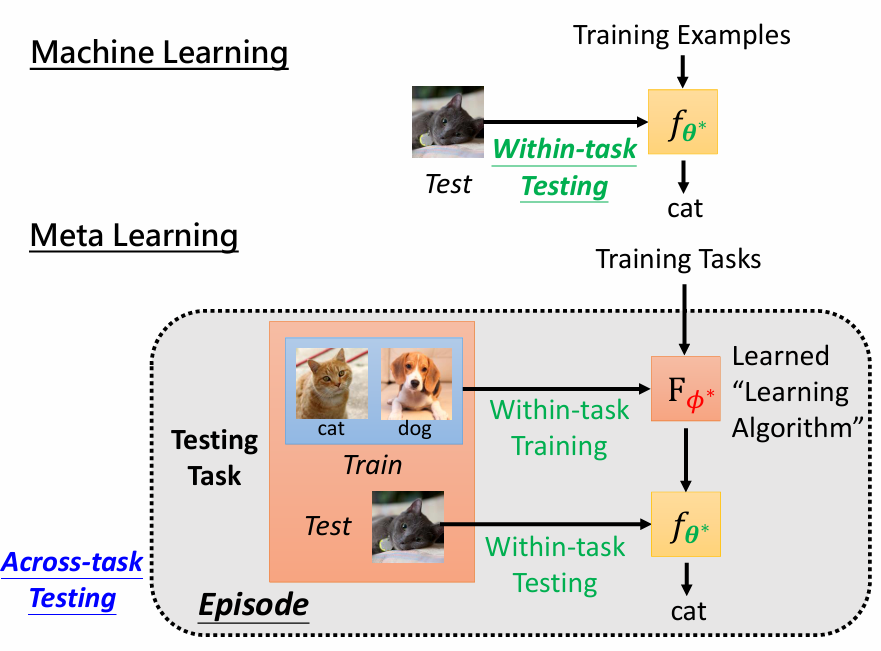
MAML 的优势

MAML 的一个关键优势在于，它学习了一个初始参数$\theta$，使得它可以通过少量梯度更新快速适应新任务。这使得它非常适合少样本学习场景，如几次样本分类。

其他元学习方法

除了 MAML，文件中还提到其他元学习方法，如基于优化器的元学习、网络架构搜索（NAS）等。这些方法都在不同程度上优化了元学习的过程，使得模型能够在少量数据的情况下快速学习。

总结

元学习的数学推导核心在于通过多个任务的训练，学习到一个通用的学习算法（或模型初始化），使得模型可以快速适应新任务。MAML 是元学习的一个经典方法，通过在元任务上进行二阶优化，使模型获得更好的泛化能力。

手写笔记

最后放几张今天的手写笔记，主要是方便查阅。