ant-design表格自动合并相同内容的单元格
表格自动合并相同内容的单元格
合并hooks
import { TableColumnProps } from 'antd'export const useAutoMergeTableCell = <T extends object>(dataSource: Array<T>,columns: Array<TableColumnProps> | Array<keyof T>
): Map<keyof T, Array<number>> => {const cellToIndexMap = new Map<keyof T, Array<number>>()const countInfoMap = new Map<keyof T, { startIndex: number; count: number; value: any } | null>()const length = dataSource.lengthconst parseColumns = columns.map((m) => {if (typeof m === 'string') {return {dataIndex: m}}return m})parseColumns.forEach((it) => {cellToIndexMap.set(it.dataIndex as keyof T, new Array(length).fill(0))countInfoMap.set(it.dataIndex as keyof T, null)})const updateCellCount = (key: string) => {const countInfo = countInfoMap.get(key as keyof T)const indexArray = cellToIndexMap.get(key as keyof T)indexArray![countInfo!.startIndex] = countInfo!.count}const calculateCount = (key: string, value: any, index: number) => {const countInfo = countInfoMap.get(key as keyof T)if (countInfo === null) {countInfoMap.set(key as keyof T, { startIndex: index, count: 1, value })} else {if (countInfo!.value === value) {countInfo!.count++} else {updateCellCount(key)countInfoMap.set(key as keyof T, { startIndex: index, count: 1, value })}}if (index === length - 1) {updateCellCount(key)}}for (let i = 0; i < length; ++i) {parseColumns.forEach((column) => {const key = column.dataIndex as stringcalculateCount(key, Reflect.get(dataSource[i], key), i)})}return cellToIndexMap
}
使用
让所有的列都进行单元格合并
// dataSource 用自己表格的数据
// columns 为你定义的列
const cellToIndexMap = useAutoMergeTableCell(dataSource, columns)
const parseColumns = columns.map((m) => {return {...m,onCell: (_, index) => {const indexArray = cellToIndexMap.get(m.dataIndex as keyof T)return {rowSpan: indexArray![index!] ?? 1}}} as TableColumnPropsreturn m
})
只想部分列进行合并
只需要传递对应的想要合并的 key 即可
const cellToIndexMap = useAutoMergeTableCell(dataSource, ['key1', 'key2'])
const parseColumns = columns.map((m) => {return {...m,onCell: (_, index) => {const indexArray = cellToIndexMap.get(m.dataIndex as keyof T)return {rowSpan: indexArray![index!] ?? 1}}} as TableColumnPropsreturn m
})
关于element-ui
如果想要适配于 element-ui,只需要把 hooks 中的 dataIndex 替换为 prop 即可。
使用:
const cellToIndexMap = useAutoMergeTableCell(dataSource, ['key1', 'key2'])
// or
// const cellToIndexMap = useAutoMergeTableCell(dataSource, columns)
spanMethods ({ row, column, rowIndex, columnIndex }) {const indexArray = cellToIndexMap.get(column.prop)return {rowSpan: indexArray![index!] ?? 1colspan: 1}
}
相关文章:

ant-design表格自动合并相同内容的单元格
表格自动合并相同内容的单元格 合并hooks import { TableColumnProps } from antdexport const useAutoMergeTableCell <T extends object>(dataSource: Array<T>,columns: Array<TableColumnProps> | Array<keyof T> ): Map<keyof T, Array<…...
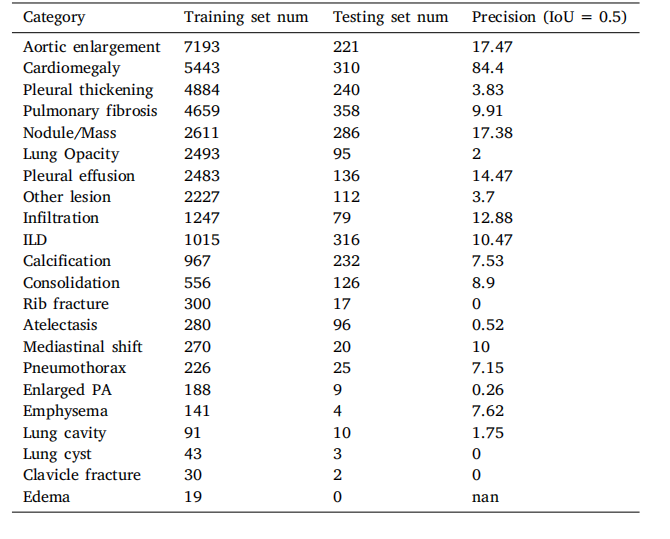
通过多模态关系图学习实现可解释的医学图像视觉问答|文献速递--Transformer架构在医学影像分析中的应用
Title 题目 Interpretable medical image Visual Question Answering via multi-modal relationship graph learning 通过多模态关系图学习实现可解释的医学图像视觉问答。 01 文献速递介绍 医学视觉问答(VQA)是医学多模态大语言模型(LL…...

从入门到精通,带你探索适合新手的视频剪辑工具
用视频来分享生活已经变成越来越多人的一种习惯,很多时候视频并不能一镜到底,所以还需要一些的修改、剪辑操作,那么这次我将介绍几款视频剪辑工具,希望能够让你分享的道路更加通畅。 1.FOXIT视频剪辑 连接直达>>https://w…...
)
线性规划------ + 案例 + Python源码求解(见文中)
目录 一、代数模型(Algebraic Models)详解1.1什么是代数模型?1.2代数模型的基本形式1.3 安装所需要的Python包--运行下述案例1.4代数模型的应用案例案例 1:市场供需平衡模型Python求解代码Python求解结果如下图:案例 2:运输问题中的线性规划模型进行数学建模分析1. 目标函…...

用Java实现人工智能
用Java实现人工智能 #Java #人工智能 #AI #机器学习 #深度学习 #数据科学 #技术博客 #编程技巧 文章目录 前言环境准备1. 安装Java2. IDE选择3. 依赖管理 数据准备模型训练模型评估分类模型评估回归模型评估模型的交叉验证 模型部署部署模型的基本步骤模型保存与加载Docker容器…...

MobaXterm使用技巧
引言 在现代IT环境中,远程管理和SSH连接已经成为管理员和开发者日常工作的重要组成部分。MobaXterm是一款功能强大的终端模拟器,它集成了多种网络工具,非常适合用于远程管理、编程和网络调试。本文将汇总一些MobaXterm的使用技巧,…...

openstack中的rabbitmq
基本概念 基础介绍 exchange:用于分发信息,有direct、fanout、topic、headers; binding:exchange、queue之间的虚拟连接,由一个或者多个routing key组成; queues:用来暂存消息,供…...

etcd三节点,其中一个坏掉了的恢复办法
一、配置etcdctl环境变量 --------------------------------------------------------------------------------------------- #其中证书实际路径和endpoints,以环境情况为准,查询方式 # ps -ef | grep etcd-cafile # ps -ef | grep etcd-servers export ETCDCTL_API3 export…...

计算机毕业设计 基于SpringBoot框架的网上蛋糕销售系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

C编程控制PC蜂鸣器方法2
在《C编程控制PC蜂鸣器》一文中,我们了解并使用了通过IO端口控制的方式操作硬件,而有些时候这对于一些朋友来说太模糊了,很容易让人迷糊,这次采用最基本的write系统调用来写入input_event数据实现相同功能。这里涉及到的input_event可参考《C编程实现键盘LED闪烁方法2》一文…...

C# SQL 辅助工具
{/// <summary>/// sql 辅助工具/// </summary>public class SqlStructureHelps{#region 增删改查/// <summary>/// 截断/// </summary>/// <typeparam name"T"></typeparam>/// <returns></returns>public static …...

eNSP简单用法
建立一个简单的拓扑图 点击绿色三角开启设备 双击设备可以进行命令编辑 视图 分为三个视图:用户视图、系统视图、接口视图 用户视图 在默认模式下就是,为<huawei> 按ctrlz返回用户视图 系统视图: 在用户视图下输入sys切换&#…...

1035. 不相交的线
1. 题目 1035. 不相交的线 2. 解题思路 题目一看是求最值,那就可以考虑用DP来做。 核心点就是确定DP数组的含义以及状态转移方程: dp数组含义:dp[i][j],nums1 前 i 个数和 nums2 前 j 个数的最大连线数dp[i][j] dp[i - 1][j …...

1.pytest基础知识(默认的测试用例的规则以及基础应用)
一、pytest单元测试框架 1)什么是单元测试框架 单元测试是指再软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试。 2)单元测试框架 java:junit和testing python:un…...

Linux常见查看文件命令
目录 一、cat 1.1. 查看文件内容 1.2. 创建文件 1.3. 追加内容到文件 1.4. 连接文件 1.5. 显示多个文件的内容 1.6. 使用管道 1.7. 查看文件的最后几行 1.8. 使用 -n 选项显示行号 1.9. 使用 -b 选项仅显示非空行的行号 二、tac 三、less 四、more 五、head 六、…...

初识 performance_schema:轻松掌握MySQL性能监控
什么是 performance_schema performance_schema 是 MySQL 5.8 版本的一个强大功能,它就像是一个内置的**“性能侦探”**,专门用来监控和分析 MySQL 服务器的资源消耗和等待情况。有了它,数据库管理员和开发者就能实时了解服务器的运行状态&a…...

linux下top命令查看和解释
怎么看top结果: top - 10:20:48 up 8 days, 14:07, 2 users, load average: 6.04, 5.82, 4.73 Tasks: 11099 total, 1 running, 10916 sleeping, 0 stopped, 1 zombie %Cpu(s): 8.9 us, 4.6 sy, 0.0 ni, 86.1 id, 0.1 wa, 0.0 hi, 0.3 si, 0.0 st K…...

换个手机IP地址是不是不一样?
在当今这个信息爆炸的时代,手机已经成为我们生活中不可或缺的一部分。而IP地址,作为手机连接网络的桥梁,也时常引起我们的关注。你是否曾经好奇,换个手机,IP地址会不会也跟着变呢?本文将深入探讨这个问题&a…...

【从计算机的发展角度理解编程语言】C、CPP、Java、Python,是偶然还是应时代的产物?
参考目录 前言什么是"computer"?计算机的大致发展历程计算机系统结构阶段(1946~1981)计算机网络和视窗阶段(1982~2007)复杂信息系统阶段(2008~today)人工智能阶段 越新的语言是越好的吗、越值得学习吗? 前言 最近读了 《Python语言程序设计基础》 这本书…...

《Google软件测试之道》笔记
介绍 GTAC:Google Test Automation Conference,Google测试自动化大会。 本书出版之前还有一本《微软测试之道》,值得阅读。 质量不是被测试出来的,但未经测试也不可能开发出有质量的软件。质量是开发过程的问题,而不…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
