数据结构——二叉树堆的专题
1.堆的概念及结构
如果有一个关键码的集合K = {K0 ,K1 ,K2 ,K3…,K(N-1) },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2*i+1且 Ki<=K2*i+2 ) i = 0,1, 2…,则称为小堆(或大堆)。将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。

2.堆的性质
(1)堆中某个结点的值总是不大于或不小于其父结点的值;
(2)堆总是一棵完全二叉树。
3.堆的实现
1.第一种
/*向上调整算法(此代码适合大堆)*/
void xiangshang(int *a,int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){int c;c = a[parent];a[parent] = a[child];a[child] = c;}/*else{break;}*/child = parent;parent = (child - 1) / 2;}
}
/*建堆(此代码会建成大堆)*/
void jiandui(int *b,int n)
{for (int i = 0; i < n; i++){xiangshang(b, i);}
}第一种建堆的具体讲解请看《四种排序方法的补充》 ,里面配有图文讲解,也有向上调整算法与向下调整算法(后面要用到)的图文讲解,希望你可以有耐心的看另一篇文章,希望我的这些讲解对你有用。
C--四种排序方法的补充-CSDN博客
2.第二种
1.创建堆所需要的模型
#include<iostream>
#include<stdlib.h>
#include<assert.h>
using namespace std;
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;size是确定我开辟的空间中,用掉了多少空间。capacity是确定我开辟了多少个空间。
2.堆的初始化
/*初始化*/
void Init(HP* ps)
{assert(ps);ps->a = NULL;ps->size = ps->capacity = 0;
}3.堆的销毁
/*销毁*/
void Destroy(HP* ps)
{assert(ps);free(ps->a);ps->a = NULL;
}这里要注意的是free(ps->a)之后,free(ps)是错误的操作。不可以销毁ps
4.插入
/*插入(通过插入会形成大堆)*/
void HeapPush(HP* ps, HPDataType x)
{assert(ps);assert(x);if (ps->capacity == 0){HPDataType* b = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (b == NULL){perror("malloc");exit(0);}ps->capacity = 4;ps->a = b;}if (ps->size == ps->capacity){HPDataType newcapacity = 2 * ps->capacity;HPDataType* b = (HPDataType*)realloc(ps->a, newcapacity * sizeof(HPDataType));if (b == NULL){perror("relloc");exit(0);}ps->a = b;ps->capacity = newcapacity;}ps->a[ps->size] = x;ps->size++;xiangshang(ps->a, ps->size - 1);
}在插入之前我要先判断我是否开辟了空间,然后判断这个空间是否已经被填满。最后再将你所需要的数字放入到最后的位置,通过向上调整算法完成排序。
5.删除元素
/*向下调整算法(此代码适合大堆)*/
void xiangxia(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if ((child + 1) < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){int c;c = a[child];a[child] = a[parent];a[parent] = c;}parent = child;child = parent * 2 + 1;}
}
/*删除元素(此代码在删除元素后还是会形成大堆)*/
void HeapPop(HP* ps)
{assert(ps);assert(ps->size > 0);HPDataType b = ps->a[0];ps->a[0] = ps->a[ps->size - 1];ps->a[ps->size - 1] = b;ps->size--;xiangxia(ps->a, ps->size, 0);
}删除元素删除的是根的元素,所以我先将根元素与最后的一个元素进行调换位置,然后让size--,(size--是因为下一次插入时,会将那个元素覆盖掉。)最后通过向下调整对这个堆重新排序,(注意:这个代码的前提是这个堆是大堆)让第二个大的坐到根的位置。
6.返还树根元素
/*返回树根元素*/
HPDataType HeapTop(HP* ps)
{assert(ps);assert(ps->size > 0);return ps->a[0];
}
7.判断是否为空
/*判断是否为空*/
bool HeapEmpty(HP* ps)
{return ps->size == 0;
}因为当我初始化之后,size便是0,只有当插入元素之后,size才会大于或等于1。
8.算多少个
/*算多少个数*/
int HeapSize(HP* ps)
{assert(ps);return ps->size;
}9.打印树的内容
/*打印树的内容*/
void HeapPrintf(HP* ps,int size)
{int i = 0;for (; i < size; i++){printf("%d ", ps->a[i]);}
}
相关文章:

数据结构——二叉树堆的专题
1.堆的概念及结构 如果有一个关键码的集合K {K0 ,K1 ,K2 ,K3…,K(N-1) },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki < K2*i1且 Ki<K2*i2 ) i 0&#…...

【C语言零基础入门篇 - 7】:拆解函数的奥秘:定义、声明、变量,传递须知,嵌套玩转,递归惊艳
文章目录 函数函数的定义与声明局部变量和全局变量、静态变量静态变量和动态变量函数的值传递函数参数的地址传值 函数的嵌套使用函数的递归调用 函数 函数的定义与声明 函数的概念:函数是C语言项目的基本组成单位。实现一个功能可以封装一个函数来实现。定义函数的…...

ClickHouse在AI领域的结合应用
文章目录 引言1.1 人工智能与大数据的融合1.2 ClickHouse在大数据平台中的地位2.1 BI与AI的融合从传统BI到智能BIAI赋能BI融合的优势实际应用案例 2.2 异构数据处理的重要性数据多样性的挑战异构数据处理的需求技术实现实际应用案例 2.3 向量检索与AIOps技术向量检索的背景AIOp…...

git push出错Push cannot contain secrets
报错原因: 因为你的代码里面包含了github token明文信息,github担心你的token会泄漏,所以就不允许你推送这些内容。 解决办法: 需要先把代码里面的github token信息删除掉,并且删掉之前的历史提交,只要包…...
OpenAI 的最强模型 o1 的“护城河”失守?谷歌 DeepMind 早已揭示相同原理
发布不到一周,OpenAI 的最新模型 o1 的“护城河”似乎已经失守。 近日,有人发现谷歌 DeepMind 早在今年 8 月发表的一篇论文,揭示了与 o1 模型极其相似的工作原理。 这项研究指出,在模型推理过程中增加测试时的计算量,…...

【胡乱念叨】大模型的“我”
下面的内容很有可能事实错误,胡说八道,前后不连贯,举例随意且未经考证 甚至 有意欺骗!嘻嘻。所以是【胡乱念叨】 文章目录 【胡乱念叨】大模型的“我”参数量和“我”什么是“我”从输入输出的观点看“我”大模型的“我”乱讨论 …...
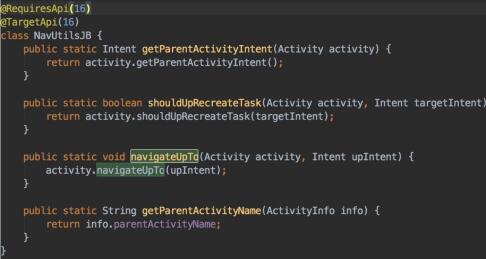
Flag_AGtivity_clear_top网页编程指南如何退出多activity程序
activity的启动模式:FLAG_ACTIVITY_CLEAR_TOP和FLAG_ACTIVITY_REORDER_TO_FRONT。 1. 如果已经启动了四个Activity:A,B,C和D。在D Activity里,我们要跳到B Activity,同时希望C finish掉,可以在start…...

克隆centos网卡uuid相同如何修改
在克隆CentOS系统后,网卡的UUID相同会导致网络配置冲突,使得网络无法正常工作。要解决这个问题,你需要为每个克隆的系统生成新的UUID。 以下是解决步骤: 进入原始CentOS系统。 找到网络配置文件的位置,通常在 /etc/s…...

C语言习题~day11
1、C程序常见的错误分类不包含:( ) A.编译错误 B.链接错误 C.栈溢出 D.运行时错误 栈溢出是运行时错误的一种,因此C程序不会将栈溢出错误单独列出来,栈溢出包含在运行时错误中。 因此:选择C 2、关于VS调…...

Ansible——Playbook基本功能???
文章目录 一、Ansible Playbook介绍1、Playbook的简单组成1)“play”2)“task”3)“playbook” 2、Playbook与ad-hoc简单对比区别联系 3、YAML文件语法:---以及多个---??使用 include 指令 1. 基本结构2. 数…...

多线程学习篇一:启动多线程的三种方式
1. 继承 Thread 类 Slf4j public class MyThread extends Thread {Overridepublic void run() {log.info("MyThread run ...");}public static void main(String[] args) {MyThread myThread new MyThread();myThread.start();} } 2. 实现 Runnable 接口 Slf4j pu…...

【专题】2024跨境出海供应链洞察-更先进供应链报告合集PDF分享(附原数据表)
原文链接:https://tecdat.cn/?p37665 当前,全球化商业浪潮促使跨境电商行业飞速发展,产业带与跨境电商接轨、平台半托管模式涌现、社交电商带来红利机会以及海外仓不断扩张,这使得产业带外贸工厂、内贸工厂、传统进出口企业和品…...

git submodule
git submodule 是 Git 提供的一种功能,用于在一个 Git 仓库中嵌套另一个 Git 仓库。它可以帮助管理和跟踪外部项目或依赖项,特别是在以下场景中非常有用: 1. 管理外部依赖 当你的项目依赖于其他外部项目或库时,可以使用 git sub…...
)
【Power Compiler手册】13.UPF多电压设计实现(3)
创建供电端口 要创建电源和地端口,请使用`create_supply_port`命令。 供电端口的名称应该是一个简单的(非层次化的)名称,并且在其定义的层次级别上是唯一的。除非指定了`-domain`选项,否则端口是在当前作用域或层次级别创建的,当前作用域中的所有电源域都可以使用创建的…...

RTX 4090 系列即将停产,RTX 5090 系列蓄势待发
据最新消息,英伟达将于今年10月正式终结其GeForce RTX 4090及RTX 4090D两款旗舰级显卡的生产线。根据行业媒体报道,英伟达及其合作厂商将从下个月开始全面停止这两款显卡的制造。 自2022年10月问世以来,GeForce RTX 4090凭借其无与伦比的GPU…...

【MySQL】使用C语言连接数据库
看到标题,可能会疑惑,我们学习的不是C吗,为什么使用C语言去连接数据库呢??实际上,这两种语言都可以连接数据库,但是C语言提供的API没有进行封装,更有利于我们学习数据库连接。面向API编程,哈哈…...
)
Vue学习记录之四(watch侦听器和watchEffect高级侦听器)
watch watch 用于侦听特定的响应式数据源(如数据、计算属性等),比如ref或者是reactive时,并在其变化时执行回调函数。它适合用于处理副作用,如 API 请求或异步操作。使用 watch 适合特定数据变化的侦听,提…...
RedisTemplate操作ZSet的API
文章目录 ⛄概述⛄常见命令有⛄RedisTemplate API❄️❄️ 向集合中插入元素,并设置分数❄️❄️向集合中插入多个元素,并设置分数❄️❄️按照排名先后(从小到大)打印指定区间内的元素, -1为打印全部❄️❄️获得指定元素的分数❄️❄️返回集合内的成员个数❄️❄…...

Android 15 正式发布至 AOSP
Google官方宣布,将于近期发布了 Android 15,而在早些时候,Google已经将其源代码推送至 Android 开源项目 (AOSP)。未来几周内,Android 15 将在受支持的 Pixel 设备上正式推出,并将于今年晚些时候在三星、Honor、iQOO、…...

IEEE Electronic Library(IEL)数据库文献检索下载介绍及个人获取IEEE文献途径
一、数据库介绍 IEEE(The Institute of Electrical and Electronics Engineers,电气电子工程师学会)是目前全球最大的非营利性专业技术学会,在全球160多个国家拥有超过45万名会员。IEEE在电气电子、计算机、半导体、通讯、电力能…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
