Python 数学建模——高斯核密度估计
文章目录
- 前言
- 原理
- 代码实例
- scipy 实现
- seaborn 实现
前言
高斯核密度估计本是一种机器学习算法,在数学建模中也可以发挥作用。本文主要讨论用它来拟合变量的概率密度,获得概率密度函数 f ( x ) f(x) f(x)。
原理
已知一个连续型随机变量 X X X 的一系列观测值 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn,我们可以用高斯核密度估计来拟合出 X X X 的概率密度函数 f ( x ) f(x) f(x)。
代码实例
scipy 实现
先给出代码,后面慢慢解释。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde# 为测试 gaussian_kde 效果,当场生成1000个beta分布的随机数
np.random.seed(114)
info = np.random.beta(a=2, b=5, size=1000)# 根据一系列观测值 info,拟合出概率密度
# 这个 gaussian_kde 有个神奇的参数 bw_method,说是计算估计器带宽的方法,可以调一下
kde = gaussian_kde(info)
x = np.linspace(min(info), max(info), 1000)
pdf = kde.evaluate(x)# 开始作图# 指定楷体以显示中文字体
plt.rcParams["font.sans-serif"] = ['KaiTi']
fig = plt.figure()
ax1 = fig.add_subplot(111, label="1")
ax2 = fig.add_subplot(111, label="2", frame_on=False)# 100 指的是 100 个直方条
ax1.hist(info,100, color='r', alpha=0.4)
ax1.set_xlabel("观测值")
ax1.set_ylabel("观测频数")ax2.plot(x, pdf, c = 'b')
ax2.set_xticks([])
ax2.set_ylabel("拟合概率密度")
ax2.yaxis.tick_right()
ax2.yaxis.set_label_position('right')
plt.show()
图画出来是这样的:

- 第 6 − 7 6-7 6−7 行,按照 β \beta β 分布生成了一个含有 1000 1000 1000 个随机数的
info。实际建模的时候,这个info应该是题目给我们的数据样本。 - 第 11 11 11 行由
info得到一个kde对象,kde.evaluate()实际上就是概率密度函数,传一个 x x x 就返回一个 f ( x ) f(x) f(x)。 - 第 12 − 13 12-13 12−13 行是取了横轴上的一些数据点获取概率密度用于后续画图,如果把
x记作 [ x 1 , ⋯ , x n ] [x_1,\cdots,x_n] [x1,⋯,xn] 那么pdf就是 [ f ( x 1 ) , ⋯ , f ( x n ) ] [f(x_1),\cdots,f(x_n)] [f(x1),⋯,f(xn)]。 - 第 18 18 18 行到最后都是在画图。
如果你觉得拟合效果不佳,可以调整gaussian_kde的bw_method参数。这个东西是采样宽度,换句话说它越大 f ( x ) f(x) f(x) 越粗糙,它越小 f ( x ) f(x) f(x) 更容易过拟合。比如我在上面的kde = gaussian_kde(info)中加入参数bw_method=0.1,画出来这样的图:

明显有些过拟合,但是很多时候我们需要这种过拟合。
seaborn 实现
Seaborn 作为一个强大的 Python 可视化库,也内置了高斯核密度估计的功能。Seaborn 只需要一行代码即可画出核密度估计图,但是它无法返回pdf或者kde等对象,也就是说我们只能看到 y = f ( x ) y=f(x) y=f(x) 的大致图像,却无法获取 f ( x 0 ) f(x_0) f(x0) ( x 0 x_0 x0 是某个具体值,比如 x 0 = 5 x_0=5 x0=5)的值。如果你的目的只是为了可视化,展示随机变量 X X X 的集中程度和均值情况,那么 seaborn 无疑是更方便的选择。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 为测试 gaussian_kde 效果,当场生成1000个beta分布的随机数
np.random.seed(114)
info = np.random.beta(a=2, b=5, size=1000)# seaborn 作图
sns.set_style("whitegrid") # 风格设置
sns.kdeplot(info,shade=True, color="g") # 概率密度函数底下填充绿色阴影
plt.show()
画出来效果如下,该图象轮廓与上面的应该是一样的。如果有两个分布类似的样本,使用 seaborn 用不同颜色画出概率密度函数,将会对比鲜明,非常好看。

除了kdeplot,seaborn 库里的distplot也可以进行高斯核密度估计,优点是它还能带上直方图。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 为测试 gaussian_kde 效果,当场生成1000个beta分布的随机数
np.random.seed(114)
info = np.random.beta(a=2, b=5, size=1000)# seaborn 作图
sns.set_style("whitegrid") # 风格设置
sns.distplot(info)
plt.show()
你也可以调整distplot的参数,hist=False不画直方图,kde=False不画概率密度函数。

相关文章:

Python 数学建模——高斯核密度估计
文章目录 前言原理代码实例scipy 实现seaborn 实现 前言 高斯核密度估计本是一种机器学习算法,在数学建模中也可以发挥作用。本文主要讨论用它来拟合变量的概率密度,获得概率密度函数 f ( x ) f(x) f(x)。 原理 已知一个连续型随机变量 X X X 的一系列…...

Flink+Spark相关记录
FlinkSpark相关记录 FlinkSQL Flink Streaming的一些点覆写RichSource、RichSink、RichMap 1.Source自动负载均衡,CDC源端加入一个全局调控的节点监控流量流速 2.Sink并发写入 3.Map与Iterator与增量迭代等用法关于Checkpoint几个用法 1.提交Commit至目的端数据库 2…...

2023 hnust 湖科大 毕业实习 报告+实习鉴定表
2023 hnust 湖科大 毕业实习 报告实习鉴定表 岗位 IT公司机房运维 实习报告 实习鉴定表 常见疑问 hnust 湖科大 毕业实习常见问题30问(2021 年7月,V0.9)-CSDN博客时间:大四开学第三四周毕业实习23年是企业(黑马&am…...

ConflictingBeanDefinitionException | 运行SpringBoot项目时报错bean定义冲突解决方案
具体报错: Caused by: org.springframework.context.annotation.ConflictingBeanDefinitionException: Annotation-specified bean name ‘CommissionMapperImpl’ for bean class [com.xxx.mapper.carrier.CommissionMapperImpl] conflicts with existing, non-co…...
【2024版】)
如何切换淘宝最新镜像源(npm)【2024版】
在使用 Node.js 和 npm 进行开发时,大家通常会遇到 npm 源速度较慢的问题。特别是当你需要安装大量依赖时,npm 官方源的速度可能不尽如人意。幸运的是,淘宝提供了一个更快速的 npm 镜像源,可以让你更快地下载和安装包。本文将介绍…...
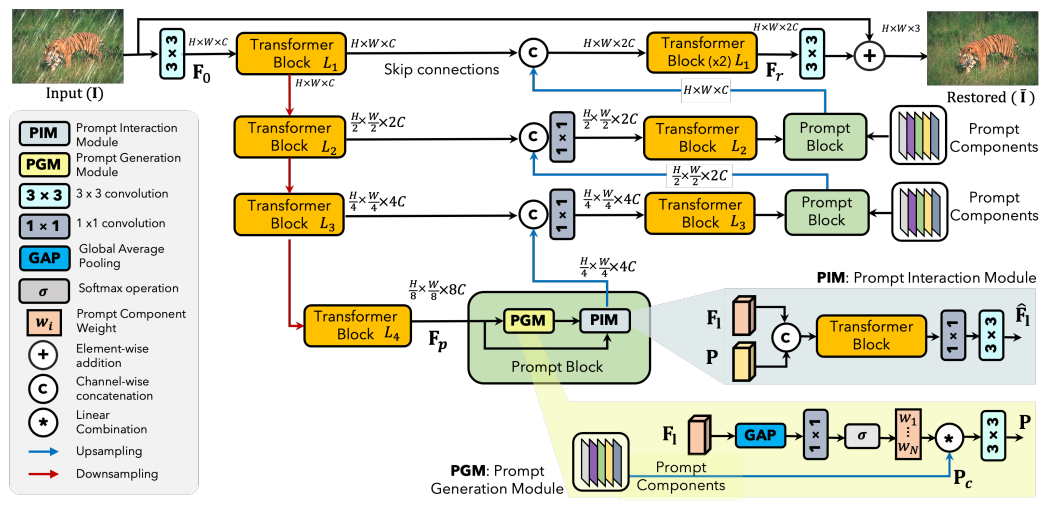
YoloV10改进策略:Block改进|PromptIR(NIPS‘2023)|轻量高效,即插即用|(适用于分类、分割、检测等多种场景)
文章目录 摘要代码详解如何在自己的论文中描述改进方法测试结果总结摘要 本文使用PromptIR框架中的PGM模块来改进YoloV10。PGM(Prompt Generation Module)模块是PromptIR框架中的一个重要组成部分,主要负责生成输入条件化的提示(prompts)。这些提示是一组可学习的参数,它…...

使用rust自制操作系统内核
一、系统简介 本操作系统是一个使用rust语言实现,基于32位的x86CPU的分时操作系统。 项目地址(求star):GitHub - CaoGaorong/os-in-rust: 使用rust实现一个操作系统内核 详细文档:自制操作系统 语雀 1. 项目特性 …...

Flink难点和高阶面试题:Flink的状态管理机制如何保证数据处理的准确性和完整性
1 Flink状态管理机制核心要素 1.1 内置状态后端 在Apache Flink中,状态管理机制是确保数据处理准确性与完整性的关键环节。其核心在于灵活且高效的状态后端,这些后端负责在分布式环境中安全地存储和访问状态数据。Flink提供了多种内置状态后端,其中RocksDB和内存状态后端最…...

【激励广告带来的广告收入与用户留存率的双重提升】
激励广告带来的广告收入与用户留存率的双重提升 ) 随着移动应用市场的竞争加剧,如何通过广告变现成为众多开发者关注的焦点。其中,激励广告(Rewarded Ads)凭借其用户友好、互动性强等特点,逐渐成为开发者的首选。那些…...

指针和引用;内联函数和普通函数
1. 指针和引用 1.1 定义和性质区别 指针是一个变量,只不过这个变量存储的是一个地址,指向内存的一个存储单元;而引用跟原来的变量实质上是同一个东西,只不过是原变量的一个别名而已。可以有const指针,常量指针可以改…...

简单题67.二进制求和 (java)20240919
题目描述: Java: class Solution {public String addBinary(String a, String b) {StringBuilder result new StringBuilder();int i a.length()-1;int j b.length()-1;int carry 0; //记录进位信息while(i>0 || j>0 || carry!0){int sum ca…...

DDD的主要流程
DDD 开发流程分为模型的建立和模型的实现两大部分,接下来是具体的流程讲解以及流程图。 1. 模型的建立 捕获行为需求:在这一阶段,团队要识别系统中需要完成的任务、操作流程、功能需求以及每个功能由谁操作、会产生什么结果。我们可以通过 …...

linux驱动开发-设备树
设备树的历史背景 背景: 在早期的嵌入式系统中,硬件配置信息通常硬编码在内核源码中,这导致了内核代码的冗长和难以维护。 为了解决这个问题,设备树(Device Tree)被引入,使得硬件描述与内核代…...

数据结构——二叉树堆的专题
1.堆的概念及结构 如果有一个关键码的集合K {K0 ,K1 ,K2 ,K3…,K(N-1) },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki < K2*i1且 Ki<K2*i2 ) i 0&#…...

【C语言零基础入门篇 - 7】:拆解函数的奥秘:定义、声明、变量,传递须知,嵌套玩转,递归惊艳
文章目录 函数函数的定义与声明局部变量和全局变量、静态变量静态变量和动态变量函数的值传递函数参数的地址传值 函数的嵌套使用函数的递归调用 函数 函数的定义与声明 函数的概念:函数是C语言项目的基本组成单位。实现一个功能可以封装一个函数来实现。定义函数的…...

ClickHouse在AI领域的结合应用
文章目录 引言1.1 人工智能与大数据的融合1.2 ClickHouse在大数据平台中的地位2.1 BI与AI的融合从传统BI到智能BIAI赋能BI融合的优势实际应用案例 2.2 异构数据处理的重要性数据多样性的挑战异构数据处理的需求技术实现实际应用案例 2.3 向量检索与AIOps技术向量检索的背景AIOp…...

git push出错Push cannot contain secrets
报错原因: 因为你的代码里面包含了github token明文信息,github担心你的token会泄漏,所以就不允许你推送这些内容。 解决办法: 需要先把代码里面的github token信息删除掉,并且删掉之前的历史提交,只要包…...
OpenAI 的最强模型 o1 的“护城河”失守?谷歌 DeepMind 早已揭示相同原理
发布不到一周,OpenAI 的最新模型 o1 的“护城河”似乎已经失守。 近日,有人发现谷歌 DeepMind 早在今年 8 月发表的一篇论文,揭示了与 o1 模型极其相似的工作原理。 这项研究指出,在模型推理过程中增加测试时的计算量,…...

【胡乱念叨】大模型的“我”
下面的内容很有可能事实错误,胡说八道,前后不连贯,举例随意且未经考证 甚至 有意欺骗!嘻嘻。所以是【胡乱念叨】 文章目录 【胡乱念叨】大模型的“我”参数量和“我”什么是“我”从输入输出的观点看“我”大模型的“我”乱讨论 …...
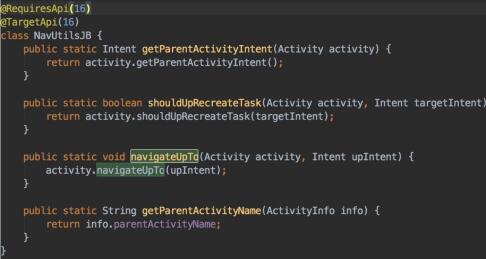
Flag_AGtivity_clear_top网页编程指南如何退出多activity程序
activity的启动模式:FLAG_ACTIVITY_CLEAR_TOP和FLAG_ACTIVITY_REORDER_TO_FRONT。 1. 如果已经启动了四个Activity:A,B,C和D。在D Activity里,我们要跳到B Activity,同时希望C finish掉,可以在start…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
