【机器学习】7 ——k近邻算法
机器学习7——k近邻
输入:实例的特征向量
输出:类别
懒惰学习(lazy learning)的代表算法
文章目录
- 机器学习7——k近邻
- 1.k近邻
- 2.模型——距离,k,分类规则
- 2.1距离——相似程度的反映
- 2.2 k值
- 分类规则
- 算法实现——kd树
- 构造平衡kd树
- 代码
- 搜索kd树——最近邻搜索
1.k近邻
少数服从多数,物以类聚
和这个实例最近的那几个实例,属于哪个类别的多,这个实例就是这个类别的
这个最近。二维举例,就是确定某个距离,画圆,圆内所有实例参与比较
算法
input:训练集T,要判断类别的实例x
output:实例x的类别
步骤:
- 根据具体的距离度量,找T中和x最近的k个实例,这k个实例构成Nk(x)
判断依据的范围- 根据分类规则,判断x的类别
2.模型——距离,k,分类规则
2.1距离——相似程度的反映

2.2 k值
决定了那些实例决定判断结果
过小的k值会使模型对噪声敏感,容易过拟合
近似误差:简化了模型
主要源于近似模型的局限性。由于真实模型往往非常复杂,难以直接求解或处理,所以采用较为简单的近似模型。而这种简化过程必然会导致与真实模型存在一定的偏差。
例如,在数值计算中,用有限项的泰勒级数去逼近一个函数,由于舍去了高阶无穷小项,就会产生近似误差。
估计误差:
一方面是由于样本的随机性。我们通常只能通过有限的样本数据来进行估计,而样本只是总体的一个部分,具有随机性,不能完全代表总体,从而导致估计值与真实值之间存在误差。
另一方面,估计方法的选择也会影响估计误差。不同的估计方法可能会产生不同大小的估计误差。
分类规则
通常是多数表决
算法实现——kd树
kd树:组织k维数据的二叉树,常用于高维空间的最近邻搜索、范围查询等问题。它通过将数据集递归划分为不同的维度,构建一棵可以快速查询的树结构。
对特征空间的划分
构造平衡kd树
-
选择维度:从数据集中选择一个轴(或维度)来划分数据。
常见的策略是每次选择不同的维度,以轮流划分不同的维度空间。
通常,这个轴是数据点的某个坐标轴,例如 x 轴或 y 轴。在每一层递归中,选择的轴通常是当前节点深度d对n取余的结果,其中 n 是数据的维度。 -
选择分割点:在选定的轴上,找到一个切分点,该切分点将数据集分为两部分。常见的选择是中位数
这可以平衡树的构造,使得左右子树中的数据量大致相同。 -
创建节点:用选定的切分点创建一个 kd 树的节点,并将数据集分为两部分,一部分包含所有在该轴上小于切分点的点,另一部分包含所有在该轴上大于切分点的点。
-
递归构建:将数据点按中位数划分为两部分,左子树包含小于中位数的点,右子树包含大于中位数的点。然后在剩余的数据上重复此过程,选择下一个维度继续递归构建。
示例
假设我们有一系列二维点:points = [(3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)]
- 首先,我们选择 x 轴作为第一层的划分轴,因为当前深度d=0,n=2,d%n=0对应 x 轴。
这里有的时候也会叫做第0层
根据x轴的数值排序[(2, 7), (3, 6), (6, 12), (9, 1), (10, 19), (13, 15), (17, 15)],中位数点为 (9, 1),作为根节点。如果双数的数据量,中间两个随便哪个都可以,但整个过程最好都一致,比如都选右侧的
- 第2层(选择y轴,即第2维度);
左子树:[(2, 7), (3, 6), (6, 12)]——对左子树按y轴排序,中位数点为 (2, 7)
右子树:[(10, 19), (13, 15), (17, 15)]——对右子树按y轴排序,中位数点为 (13, 15)
- 第3层(选择x轴)左子树继续递归:
[(3, 6), (6, 12)]——中位数点为 == (6, 12)==
右子树为 == (17, 15)==
结果x (9, 1)/ \
y (2, 7) (13, 15)/ / \
x (6, 12) (10, 19) (17, 15)/
y(3, 6)代码
class Node:def __init__(self, point, left=None, right=None):self.point = point # 节点存储的点self.left = left # 左子树self.right = right # 右子树def create_kd_tree(data, depth=0):if not data:return None# 选择切分轴(根据深度选择维度)k = len(data[0]) # 数据的维度axis = depth % k # 当前的切分轴# 对数据按照切分轴的值进行排序,并选择中位数对应的点作为切分点data.sort(key=lambda x: x[axis])median = len(data) // 2 # 中位数的索引# 创建节点,并递归地创建子树return Node(point=data[median],left=create_kd_tree(data[:median], depth + 1),right=create_kd_tree(data[median + 1:], depth + 1))# 示例数据(每个点是二维空间中的一个坐标)
points = [(2, 3), (5, 4), (1, 8), (4, 7), (6, 3), (5, 2)]
kd_tree = create_kd_tree(points)# 函数用于打印Kd树(递归)
def print_kd_tree(node, depth=0, prefix="Root"):if node is not None:print(f"{prefix}('x{depth % 2 + 1}': {node.point})")print_kd_tree(node.left, depth + 1, prefix="L---")print_kd_tree(node.right, depth + 1, prefix="R---")# 打印Kd树
print_kd_tree(kd_tree)
搜索kd树——最近邻搜索
- 从根节点开始:将查询点与根节点进行比较。
- 决定搜索方向:根据查询点在当前分割轴上的值与节点在该轴上的值的比较结果,决定是向左子树搜索还是向右子树搜索
- 递归搜索:在选定的子树中递归地执行步骤1和2,直到达到叶子节点。
- 回溯:在回溯过程中,检查是否有可能在之前跳过的子树中找到更近的邻居。这通常涉及到检查当前节点的另一个子树(如果之前没有搜索过),并考虑是否有可能在该子树中找到比当前最近点更近的点。这通常通过计算一个“边界框”的距离来实现,该边界框包围了未搜索的子树中的所有点。
- 更新最近点:如果在搜索过程中找到了比当前最近点更近的点,则更新最近点。
- 继续回溯:继续回溯,直到回到根节点。
假设我们使用KD树进行最近邻查找,查询点是 (12, 8)。具体过程如下:
x (9, 1)/ \
y (2, 7) (13, 15)/ / \
x (6, 12) (10, 19) (17, 15)/
y(3, 6)根节点比较:我们在x轴上选择 (9, 1) 作为根节点,比较 (12, 8) 在右边12>9,因此进入右子树。
第二层比较:在y轴上比较,选择的点是 (13, 15),查询点 (12, 8) 位于左侧8<15,因此进入左子树。
第三层比较:进入x轴上选择 (10, 19),查询点 (12, 8) 在右侧12>10,进入右子树(没有,开始回溯)。
叶节点返回:到达叶节点后,返回当前最近邻点(此时为 (10, 19))。
回溯:回溯到(13, 15),发现更近,更新当前最近邻点(此时为(13, 15))
查看另一子树:查看(17, 15),不更新,继续回溯
到根节点: (9, 1),还是(13, 15),所以结果是(13, 15)
# 导入数学库用于计算距离
import math# 定义KD树节点类
class KDNode:def __init__(self, point, axis=0):# 节点存储的数据点self.point = point# 左子树self.left = None# 右子树self.right = None# 划分维度self.axis = axis# 构建KD树
def build_kd_tree(points, depth=0):# 如果当前数据集为空,则返回空节点if not points:return None# 根据深度确定划分维度axis = depth % len(points[0])# 按照当前维度排序数据点points.sort(key=lambda point: point[axis])# 找到中位数的位置median_idx = len(points) // 2# 创建当前维度的节点node = KDNode(points[median_idx], axis)# 递归构建左子树node.left = build_kd_tree(points[:median_idx], depth + 1)# 递归构建右子树node.right = build_kd_tree(points[median_idx + 1:], depth + 1)# 返回当前节点return node# 打印KD树结构
def print_kd_tree(node, depth=0):if node is None:return# 缩进显示层次结构indent = " " * depthprint(f"{indent}Point: {node.point}, Axis: {node.axis}")# 递归打印左子树print_kd_tree(node.left, depth + 1)# 递归打印右子树print_kd_tree(node.right, depth + 1)# 在KD树中搜索最近邻点
def search_kd_tree(node, target, best=None):if node is None:return best# 当前节点的划分维度axis = node.axis# 根据目标点与当前节点在划分维度上的值决定先访问哪一侧if target[axis] < node.point[axis]:next_node = node.leftother_node = node.rightelse:next_node = node.rightother_node = node.left# 递归搜索下一层best = search_kd_tree(next_node, target, best)# 更新最佳结果if best is None or distance(target, node.point) < distance(target, best):best = node.point# 计算目标点与当前节点在划分维度上的距离dist = abs(target[axis] - node.point[axis])# 如果这个距离小于当前最佳结果的距离,则需要检查另一侧if dist < distance(target, best):best = search_kd_tree(other_node, target, best)return best# 计算两点之间的欧氏距离
def distance(p1, p2):return math.sqrt(sum((a - b)**2 for a, b in zip(p1, p2)))# 定义一组二维数据点
points = [(3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)]
# 构建KD树
root = build_kd_tree(points)
# 打印KD树结构
print("KD Tree:")
print_kd_tree(root)# 定义一个目标点
target_point = (12, 8)
# 在KD树中搜索最近邻点
result = search_kd_tree(root, target_point)
# 输出结果
print(f"Nearest point to {target_point}: {result}")
相关文章:

【机器学习】7 ——k近邻算法
机器学习7——k近邻 输入:实例的特征向量 输出:类别 懒惰学习(lazy learning)的代表算法 文章目录 机器学习7——k近邻1.k近邻2.模型——距离,k,分类规则2.1距离——相似程度的反映2.2 k值分类规则 算法实…...

2024.09.09 校招 实习 内推 面经
🛰️ :neituijunsir 交* 流*裙 ,内推/实习/校招汇总表格 1、校招 | 佑驾创新 MINIEYE 2025校园招聘正式启动(内推) 校招 | 佑驾创新 MINIEYE 2025校园招聘正式启动(内推) 2、校招 | 长安汽…...

浅谈Linux中的环回设备
什么是环回设备 环回设备(loop device) 是 Linux 系统中一种特殊的虚拟设备,它允许你将一个普通的文件当作块设备来操作。这意味着,借助环回设备,文件可以模拟为一个磁盘或分区,供系统读写。这种机制非常有…...

聚焦汽车智能化与电动化,亚洲领先的汽车工业技术博览会 2025年11月与您相约 AUTO TECH 华南展
抢占市场先机︱聚焦汽车智能化与电动化,亚洲领先的汽车工业技术博览会 2025年11月与您相约 AUTO TECH 华南展 随着汽车智能化与电动化的迅猛发展,汽车电子技术、车用功率半导体技术、智能座舱技术、轻量化技术/材料、软件定义汽车、EV/HV技术、测试测量技…...

(史上最全)线程池
线程池 文章目录 线程池一,前言二,线程池三,参数四,线程池的实现原理5.线程池的使用案例(自定义线程池)6.使用Executors 创建常见的功能线程池1.固定大小线程池2.定时线程3.可缓存线程池4.单线程化线程池 一,前言 虽然…...
详解:从理论到实践,这一篇就够了)
【ShuQiHere】 支持向量机(SVM)详解:从理论到实践,这一篇就够了
📖 【ShuQiHere】 在现代机器学习课程中,支持向量机(SVM) 是不可或缺的一部分。它不仅在分类任务中有出色表现,还能灵活处理回归问题。尽管看似复杂,SVM 背后的思想却深刻而优雅。今天我们将全面探讨**支持…...

log4j2线程级动态日志级别
详见 参考 着重说明: DynamicThresholdFilter: 配置长这样:配置解释链接 <DynamicThresholdFilter key"logLevel" defaultThreshold"ERROR" onMatch"ACCEPT" onMismatch"DENY"><KeyVa…...
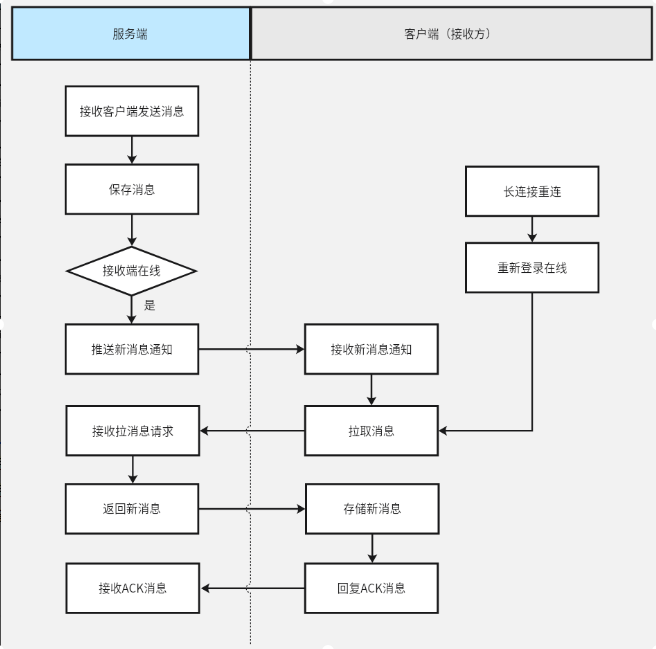
百度Android IM SDK组件能力建设及应用
作者 | 星途 导读 移动互联网时代,随着社交媒体、移动支付、线上购物等行业的快速发展,对即时通讯功能的需求不断增加。对于各APP而言,接入IM SDK(即时通讯软件开发工具包)能够大大降低开发成本、提高开发效率&#…...

CSS-Grid布局详解
前言 Grid 栅格布局 是 CSS 语言中非常强大的种布局,它提供了丰富的工具属性,可以轻松实现复杂且灵活的布局设计,因此想要完美使用CSS Grid 也有一定的难度和复杂性,我自己也是花了不少时间才真正掌握它的使用,在这篇…...

Give azure openai an encyclopedia of information
题意:给 Azure OpenAI 提供一部百科全书式的信息 问题背景: I am currently dabbling in the Azure OpenAI service. I want to take the default model and knowledge base and now add on to it my own unique information. So, for example, for mak…...

Nginx越界读取缓存漏洞(CVE-2017-7529)
漏洞原理: 影响版本内默认配置模块的Nginx只需要开启缓存,攻击者可以通过发送包含恶意构造range域的header请求进行远程攻击造成信息泄露。 影响范围: Nginx 0.5.6 – 1.13.2 漏洞复现: 开启靶场,访问8080端口 中间…...

【MySQL】查询语句之inner、left、right、full join 的区别
前言: INNER JOIN 和 OUTER JOIN 是SQL中常用的两种连接方式,用于从两表活多表中提取相关的数据。两者区别主要在于返回的 结果集 如何处理 匹配 与 不匹配 的行。 目录 1、INNER JOIN 2、OUTER JOIN 3、总结 1、INNER JOIN 称为内连接,只…...
Submariner 部署全过程
Submariner 部署全过程 部署集群配置 broker 集群: pod-cidr:11.244.0.0/16 service-cidr 11.96.0.0/12 broker 172.100.0.109 node 172.100.0.108 集群 1( pve3 ): pod-cidr:10.244.0.0/16 service-…...

驼峰命名法
一、驼峰命名法简介 驼峰命名法(Camel Case)是一种在编程和人类语言中广泛使用的书写方式,通过将单词连接在一起,并使每个单词的首字母大写来表示复合词或短语。这种命名法有小驼峰法和大驼峰法两种变种。 二、小驼峰命名法&…...

Android IME输入法启动显示隐藏流程梳理
阅读Android AOSP 12版本代码,对输入法IME整体框架模块进行学习梳理,内容包含输入法框架三部分IMM、IMMS、IMS的启动流程、点击弹出流程、显示/隐藏流程,以及常见问题和调试技巧。 1. IME整体框架 IME整体分为三个部分…...

Java 入门指南:JVM(Java虚拟机)——类的生命周期与加载过程
文章目录 类的生命周期类加载过程1)载入(Loading)2)验证(Verification)文件格式验证符号引用验证 3)准备(Preparation)4)解析(Resolution…...
敌人关卡生成器的设计和开发)
Unity射击游戏开发教程:(36)敌人关卡生成器的设计和开发
丰富多样地游戏关卡生成器能自动生成不同的关卡地图和游戏内容,以增加游戏的可玩性和挑战性。关卡生成可以基于随机算法或者预设的规则生成不同的地图布局、敌人位置、道具位置等。 定义关卡生成器WaveSpawner 如何设置通用的 Wave Spawner?我将此 Wave Spawner 脚本附加到…...

AI对汽车行业的冲击和比亚迪新能源汽车市场占比
人工智能(AI)对汽车行业的冲击正在迅速改变该行业的面貌,从智能驾驶到生产自动化,再到个性化的消费者体验,AI带来的技术革新在各个层面影响着汽车产业。与此同时,新能源汽车市场,特别是以比亚迪…...

2024年中国电子学会青少年软件编程(Python)等级考试(一级)核心考点速查卡
考前练习: 2024年06月中国电子学会青少年软件编程(Python)等级考试试卷(一级)答案 解析-CSDN博客 2024年03月中国电子学会青少年软件编程(Python)等级考试试卷(一级)答…...

游戏开发引擎__游戏场景(灯光,摄像机)
1.灯光 重要参数介绍 类型: 控制灯光的类型,有“定向”“点”“区域”和“聚光”4种模式。颜色: 控制灯光的颜色。模式: 控制灯光的光照模式,有“实时”“混合”和“烘焙”3种模式。强度: 控制灯光的明亮程度。间接乘数: 改变间接光的强度。阴影类型: …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
