A. Make All Equal
time limit per test
1 second
memory limit per test
256 megabytes
You are given a cyclic array a1,a2,…,ana1,a2,…,an.
You can perform the following operation on aa at most n−1n−1 times:
- Let mm be the current size of aa, you can choose any two adjacent elements where the previous one is no greater than the latter one (In particular, amam and a1a1 are adjacent and amam is the previous one), and delete exactly one of them. In other words, choose an integer ii (1≤i≤m1≤i≤m) where ai≤a(imodm)+1ai≤a(imodm)+1 holds, and delete exactly one of aiai or a(imodm)+1a(imodm)+1 from aa.
Your goal is to find the minimum number of operations needed to make all elements in aa equal.
Input
Each test contains multiple test cases. The first line contains the number of test cases tt (1≤t≤5001≤t≤500). The description of the test cases follows.
The first line of each test case contains a single integer nn (1≤n≤1001≤n≤100) — the length of the array aa.
The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤n1≤ai≤n) — the elements of array aa.
Output
For each test case, output a single line containing an integer: the minimum number of operations needed to make all elements in aa equal.
Example
Input
Copy
7
1
1
3
1 2 3
3
1 2 2
5
5 4 3 2 1
6
1 1 2 2 3 3
8
8 7 6 3 8 7 6 3
6
1 1 4 5 1 4
Output
Copy
0 2 1 4 4 6 3
Note
In the first test case, there is only one element in aa, so we can't do any operation.
In the second test case, we can perform the following operations to make all elements in aa equal:
- choose i=2i=2, delete a3a3, then aa would become [1,2][1,2].
- choose i=1i=1, delete a1a1, then aa would become [2][2].
It can be proven that we can't make all elements in aa equal using fewer than 22 operations, so the answer is 22.
解题说明:水题,统计数列中那个数字出现的次数最多,删除其他数字就是答案。可以用数组来记录每个数字出现的次数,找出最大值再用总次数相减即可。
#include<stdio.h>int main()
{int t;scanf("%d", &t);while (t--){int n, m = 0;scanf("%d", &n);int a[101];for (int i = 0; i < n; i++){a[i] = 0;}for (int i = 0; i < n; i++){int x;scanf("%d", &x);a[x - 1]++;if (a[x - 1] > m){m = a[x - 1];}}printf("%d\n", n - m);}return 0;
}相关文章:

A. Make All Equal
time limit per test 1 second memory limit per test 256 megabytes You are given a cyclic array a1,a2,…,ana1,a2,…,an. You can perform the following operation on aa at most n−1n−1 times: Let mm be the current size of aa, you can choose any two adjac…...

业务安全治理
业务安全治理 1.账号安全撞库账户盗用 2.爬虫与反爬虫3.API网关防护4.钓鱼与反制钓鱼发现钓鱼处置 5.大数据风控风控介绍 1.账号安全 撞库 撞库分为垂直撞库和水平撞库两种,垂直撞库是对一个账号使用多个不同的密码进行尝试,可以理解为暴力破解&#x…...
HelpLook VS GitBook,在线文档管理工具对比
在线文档管理工具在当今时代非常重要。随着数字化时代的到来,人们越来越依赖于电子文档来存储、共享和管理信息。无论是与团队合作还是与客户分享,人们都可以轻松地共享文档链接或通过设置权限来控制访问。在线文档管理工具的出现大大提高了工作效率和协…...

docker面经
docker面经在线链接 docker面经在线链接🔗: (https://h03yz7idw7.feishu.cn/wiki/N3CVwO3kMifLypkJqnic9wNynKh)...

Python 中的 Kombu 类库
Kombu 是一个用于 Python 的消息队列库,提供了高效、灵活的消息传递机制。它是 Celery 的核心组件之一,但也可以单独使用。Kombu 支持多种消息代理(如 RabbitMQ、Redis、Amazon SQS 等),并提供了消息生产者和消费者的功…...

safepoint是什么?有什么用?
在JVM中,safepoint(安全点)是一个非常重要的概念,特别是在垃圾回收(GC)和其他需要暂停所有应用线程的操作中。 什么是safepoint Safepoint是JVM执行过程中一个特定的位置,在这个位置上&#x…...

axios相关知识点
一、基本概念 1、基于Promise:Axios通过Promise实现异步请求,避免了传统回调函数导致的“回调地狱”问题,使得代码更加清晰和易于维护。 2、跨平台:Axios既可以在浏览器中运行,也可以在Node.js环境中使用,为前后端开…...

LeetCode 面试经典150题 67.二进制求和
415.字符串相加 思路一模一样 题目:给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 eg: 输入a“1010” b“1011” 输出“10101” 思路:从右开始遍历两个字符串,因为右边是低位先运算。如果…...

Dell PowerEdge 网络恢复笔记
我有一台Dell的PowerEdge服务器,之前安装了Ubuntu 20 桌面版。突然有一天不能开机了。 故障排查 Disk Error 首先是看一下机器的正面,有一个非常小的液晶显示器,只能显示一排字。 上面显示Disk Error,然后看挂载的硬盘仓&#…...

Java面试——集合篇
1.Java中常用的容器有哪些? 容器主要包括 Collection 和 Map 两种,Collection 存储着对象的集合,而 Map 存储着键值对(两个对象)的映射表。 如图: 面试官追问:说说集合有哪些类及他们各自的区别和特点? S…...

算法【双向广搜】
双向广搜常见用途 1:小优化。bfs的剪枝策略,分两侧展开分支,哪侧数量少就从哪侧展开。 2:用于解决特征很明显的一类问题。特征:全量样本不允许递归完全展开,但是半量样本可以完全展开。过程:把…...

javascript检测数据类型的方法
1. typeof 运算符 typeof是一个用来检测变量的基本数据类型的运算符。它可以返回以下几种类型的字符串:“undefined”、“boolean”、“number”、“string”、“object”、“function” 和 “symbol”(ES6)。需要注意的是,对于 n…...

生信初学者教程(五):R语言基础
文章目录 数据类型整型逻辑型字符型日期型数值型复杂数数据结构向量矩阵数组列表因子数据框ts特殊值缺失值 (NA)无穷大 (Inf)非数字 (NaN)安装R包学习材料R语言是一种用于统计计算和图形展示的编程语言和软件环境,广泛应用于数据分析、统计建模和数据可视化。1991年:R语言的最…...

深度学习计算
一、层和块 块可以描述单个层、多个层组成的组件或整个模型。 通过定义块,组装块,可以实现复杂的神经网络。 一个块可以由多个class组成。 其实就是 自己定义神经网络net,自己定义层的顺序和具体的init、 forward函数。 层和块的顺序由sequen…...

Hexo博客私有部署Twikoo评论系统并迁移评论记录(自定义邮件回复模板)
部署 之前一直使用的artalk,现在想改用Twikoo,采用私有部署的方式。 私有部署 (Docker) 端口可以根据实际情况进行修改 docker run --name twikoo -e TWIKOO_THROTTLE1000 -p 8100:8100 -v ${PWD}/data:/app/data -e TWIKOO_PORT8100 -d imaegoo/twi…...

Vue.js 与 Flask/Django 后端配合:构建现代 Web 应用的最佳实践
Vue.js 与 Flask/Django 后端配合:构建现代 Web 应用的最佳实践 在现代 Web 开发中,前后端分离的架构已经成为主流。Vue.js 作为一个渐进式 JavaScript 框架,因其灵活性和易用性而广受欢迎。而 Flask 和 Django 则是 Python 生态中两个非常流…...
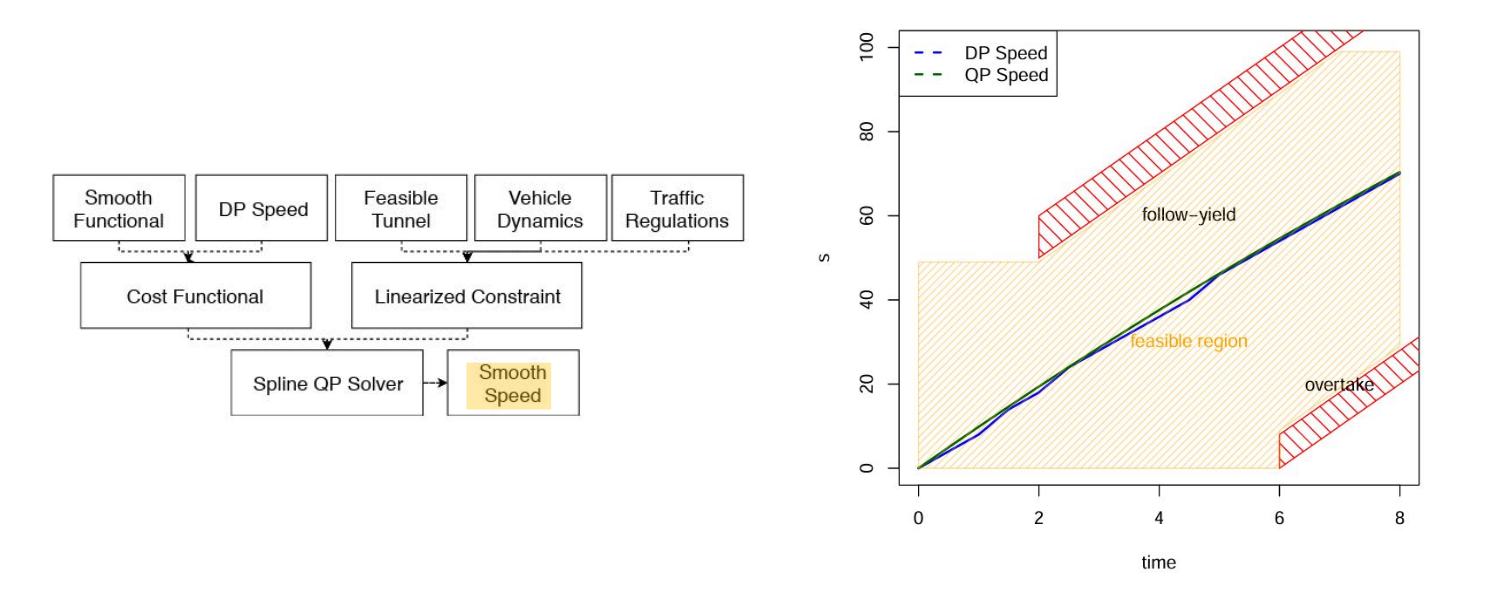
【笔记】自动驾驶预测与决策规划_Part3_路径与轨迹规划
文章目录 0. 前言1. 基于搜索的路径规划1.1 A* 算法1.2 Hybrid A* 算法 2. 基于采样的路径规划2.1 Frent Frame方法2.2 Cartesian →Frent 1D ( x , y ) (x, y) (x,y) —> ( s , l ) (s, l) (s,l)2.3 Cartesian →Frent 3D2.4 贝尔曼Bellman最优性原理2.5 高速轨迹采样——…...

Shiro-721—漏洞分析(CVE-2019-12422)
文章目录 Padding Oracle Attack 原理PKCS5填充怎么爆破攻击 漏洞原理源码分析漏洞复现 本文基于shiro550漏洞基础上分析,建议先看上期内容: https://blog.csdn.net/weixin_60521036/article/details/142373353 Padding Oracle Attack 原理 网上看了很多…...

【Python语言初识(一)】
一、python简史 1.1、python的历史 1989年圣诞节:Guido von Rossum开始写Python语言的编译器。1991年2月:第一个Python编译器(同时也是解释器)诞生,它是用C语言实现的(后面),可以调…...

Python 中的方法解析顺序(MRO)
在 Python 中,MRO(Method Resolution Order,方法解析顺序)是指类继承体系中,Python 如何确定在调用方法时的解析顺序。MRO 决定了在多继承环境下,Python 如何寻找方法或属性,即它会根据一定规则…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
