【C语言-数据结构】顺序表的基本操作
顺序表的基本操作
【建议:如果对结构体还不太理解的话可以先看 C语言-结构体 这篇文章】
插入操作
ListInsert(&L,i,e):插入操作,在表 L 中的第 i 个位置上插入指定元素 e
代码实现
#include <stdio.h>
#include <stdbool.h>
#define MaxSize 10typedef struct{int data[MaxSize];int length;
}SqList;void InitList(SqList* L){L->length = 0;
}bool ListInsert(SqList* L, int i, int e){if(i<1 || i>length+1){return false;}if(L->length >= MaxSize){return false;}for(int j = L.length; j >= i; j--){ //将第i个元素及之后的元素后移L->data[j] = L->data[j-1];}L->data[i-1] = e;L->length++;return true;
}int main(){SqList L;InitList(&L);//...向顺序表中插入一些元素...ListInsert(&L,3,3);return 0;
}
时间复杂度分析
- 最好情况:新元素插入到表尾,不需要移动元素
i = n+1,循环 0 次 ➡️ 最好时间复杂度 = O(1) - 最坏情况:新元素插入到表头,需要将原有的 n 个元素全都向后移动
i = 1,循环 n 次 ➡️ 最坏时间复杂度 = O(n) - 平均情况:假设新元素插入到任何一个位置的概率相同,即 i = 1,2,3,…,length+1 的概率都是 p = 1 n + 1 p=\frac{1}{n+1} p=n+11
i = 1 时,循环 n 次;i = 2 时,循环 n-1 次,…… ,i = n+1 时,循环 0 次
平均循环次数 = np + (n-1)p + …… + 1·p = n ( n + 1 ) 2 1 n + 1 \frac{n(n+1)}{2}\frac{1}{n+1} 2n(n+1)n+11 = n 2 \frac{n}{2} 2n ➡️ 平均时间复杂度 = O(n)
删除操作
ListDelete(&L,i,&e):删除操作,删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值
代码实现
#include <stdio.h>
#include <stdbool.h>
#define MaxSize 10typedef struct{int data[MaxSize];int length;
}SqList;void InitList(SqList* L){L->length = 0;
}bool ListDelete(SqList* L, int i, int* e){if(i<1 || i>L->length){return false;}e = L->data[i-1];for(int j = i; j < L; j++){L->data[j-1] = L->data[j];}L->length--;return true;
}int main(){SqList L;InitList(&L);//...向顺序表中插入一些元素...int e = -1;if(ListDelete(&L, 3, &e)){printf("已删除第3个元素,删除元素值为%d\n",e);}else{printf("位序i不合法,删除失败\n");}return 0;
}
时间复杂度分析
- 最好情况:删除表尾元素,不需要移动元素
i = n,循环 0 次 ➡️ 最好时间复杂度 = O(1) - 最坏情况:删除表头元素,需要将后续的 n-1 个元素全都向前移动
i = 1,循环 n-1 次 ➡️ 最坏时间复杂度 = O(n) - 平均情况:假设删除任何一个元素的概率相同,即 i = 1,2,3,…,length 的概率都是 p = 1 n p=\frac{1}{n} p=n1
i = 1 时,循环 n-1 次;i = 2 时,循环 n-2 次,…… ,i = n 时,循环 0 次
平均循环次数 = (n-1)p + …… + 1·p = n ( n − 1 ) 2 1 n \frac{n(n-1)}{2}\frac{1}{n} 2n(n−1)n1 = n − 1 2 \frac{n-1}{2} 2n−1 ➡️ 平均时间复杂度 = O(n)
按位查找操作
GetElem(L,i):按位查找操作,获取表 L 中第 i 个位置的元素的值
代码实现
ElemType GetElem(SqList* L, int i){return L->data[i-1];
}
时间复杂度:O(1)
按值查找操作
LocateElem(L,e):按值查找操作,在表 L 中查找具有给定关键字值的元素
代码实现
//在顺序表L中查找第一个元素值等于e的元素,并返回其位序
int LocateElem(SqList* L, int e){for(int i = 0; i < L.length; i++){if(L->data[i] == e){return i+1;}}return 0;
}
时间复杂度分析
- 最好情况:目标元素在表头
循环 1 次 ➡️ 最好时间复杂度 = O(1) - 最坏情况:目标元素在表尾
循环 n 次 ➡️ 最坏时间复杂度 = O(n) - 平均情况:假设目标元素出现在任意一个位置的概率相同,即都是 p = 1 n p=\frac{1}{n} p=n1
平均循环次数 = n + 1 2 \frac{n+1}{2} 2n+1 ➡️ 平均时间复杂度 = O(n)
本文主要参考《王道计算机考研 数据结构》课程视频
相关文章:

【C语言-数据结构】顺序表的基本操作
顺序表的基本操作 【建议:如果对结构体还不太理解的话可以先看 C语言-结构体 这篇文章】 插入操作 ListInsert(&L,i,e):插入操作,在表 L 中的第 i 个位置上插入指定元素 e 代码实现 #include <stdio.h> #include <stdbool.…...

使用Renesas R7FA8D1BH (Cortex®-M85)实现多功能UI
目录 概述 1 系统框架介绍 1.1 模块功能介绍 1.2 UI页面功能 2 软件框架结构实现 2.1 软件框架图 2.1.1 应用层API 2.1.2 硬件驱动层 2.1.3 MCU底层驱动 2.2 软件流程图 4 软件功能实现 4.1 状态机功能核心代码 4.2 页面功能函数 4.3 源代码文件 5 功能测试 5.1…...

【java】常见限流算法原理及应用
目录 前言 限流的作用 4种常见限流算法 固定窗口限流 基本原理 简单实现 优点和缺点 滑动窗口限流 基本原理 简单实现 优点和缺点 漏桶限流 基本原理 简单实现 优点和缺点 令牌桶限流 基本原理 简单实现 优点和缺点 算法比较与选择 前言 在现代分布式系统…...
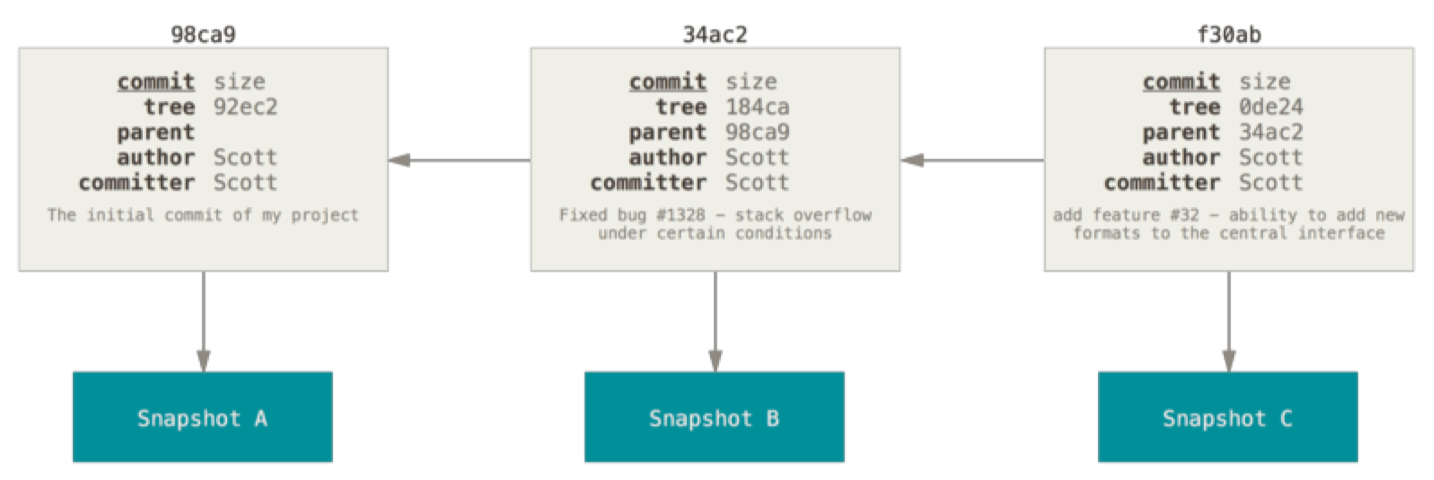
Git 原理(提交对象)(结合图与案例)
Git 原理(提交对象) 这一块主要讲述下 Git 的原理。 在进行提交操作时,Git 会保存一个提交对象(commit object): 该提交对象会包含一个指向暂存内容快照的指针; 该提交对象还包含了作者的姓…...

STM32如何修改外部晶振频率和主频
对于STM32F10x系列的单片机,除了STM32F10x_CL单片机,其它的单片机一般外部晶振HSE的时钟频率都默认是8MHz。如果我们使用的外部晶振为12Mhz,那么可以把上图绿色标记改为:12000000 72MHz的主频8MHz的外部晶振HSE*倍频系数9。当然如果像上面把外…...

【JAVA入门】Day48 - 线程池
【JAVA入门】Day48 - 线程池 文章目录 【JAVA入门】Day48 - 线程池一、线程池的主要核心原理二、自定义线程池三、线程池的大小 我们之前写的代码都是,用到线程的时候再创建,用完之后线程也就消失了,实际上这是不对的,它会浪费计算…...

图像亮度均衡算法
图像亮度均衡算法 图像亮度均衡算法的作用是提升图像的对比度和细节,使得图像的亮度分布更加均匀,从而改善视觉效果。通过调整亮度值,可以更好地揭示图像中的细节,尤其在低光或高光条件下的图像处理。 常见的图像亮度均衡算法包括…...

C++中的new与delete
目录 1.简介 2.底层 1.简介 new是升级版的malloc,它会先开空间再去调用构造函数。 delete是升级版的free,它会先调用析构函数再free掉空间。 class A { public:A(int a10, int b10){a a1;b b1;}private:int a;int b; };int main() {//new会先开空间…...

在HTML中添加视频
在HTML中添加视频,你可以使用<video>标签。这个标签允许你在网页上嵌入视频内容,并支持多种视频格式,如MP4、WebM和Ogg等。不过,由于浏览器对视频格式的支持程度不同,因此通常建议提供多种格式的视频文件&#x…...

YoloV10 训练自己的数据集(推理,转化,C#部署)
目录 一、下载 三、开始训练 train.py detect.py export.py 超参数都在这个路径下 四、C#读取yolov10模型进行部署推理 如下程序是用来配置openvino 配置好引用后就可以生成dll了 再创建一个控件,作为显示 net framework 4.8版本的 再nuget工具箱里下载 …...

Science Robotic 内在触觉实现直观的物理人机交互
触觉传感器和电子皮肤是为机器人提供物理交互感的常见设备,但当用于机器人的大面积覆盖时,它们会变得复杂且昂贵。德国宇航中心近期发表的Science Robotics研究工作,使用内部高分辨率关节力扭矩传感器,在机械臂中实现了固有的全身…...

string类(C++)
哈喽各位!,久违了,最近怎么样捏,本次进入C的string类,加油加油呀! 随记:鼓励创新,宽容失败! 1.标准库的string类 1.1string类的了解 string的文献参考链接-->strin…...

【C语言】自定义类型——结构体
目录 一、结构体的类型的声明 二、结构体变量的创建和初始化 三、匿名结构体类型 四、结构体自引用 五、结构体内存对齐 (1)对齐规则 (2)计算结构体大小练习 (3)需要内存对齐的原因 (4…...

MySQL练手题--日期连续类型(困难)
一、准备工作 Create table If Not Exists Failed (fail_date date); Create table If Not Exists Succeeded (success_date date); Truncate table Failed; insert into Failed (fail_date) values (2018-12-28); insert into Failed (fail_date) values (2018-12-29); inser…...

【AD24报错】运行DRC后出现 Un-Routed Net Constraint ### Net Not Assigned 的解决方案
AD24在运行PCB设计规则检查(DRC)后报错 Un-Routed Net Constraint ### Net Not Assigned 的解决方案 一、解决方案二、可能会报错Dead Copper的因素三、可能会报错Un-Routed Net Constraint的因素 Un-Routed Net Constraint ### Net Not Assigned 的解决…...

Linux嵌入式驱动开发指南(速记版)---Linux基础篇
第一章 Ubuntu系统入门 1.1 Linux磁盘管理 1.1.1 Linux磁盘管理基本概念 关键词: Linux 磁盘管理 挂载点 /etc/fstab文件 分区 ls /dev/sd* 联系描述: Linux 磁盘管理体系通过“挂载点”概念替代了 Windows 中的“分区”概念,将硬盘部分以文…...

PDF——压缩大小的方法
方法一:QQ浏览器->格式转换->PDF转纯图PDF...

无监督神经组合优化的扩散模型框架
文章目录 Abstract1. Introduction2. Problem Description2.1 无监督神经组合优化3. Neural Probabilistic Optimization Objective for Approximate Likelihood Models3.1 具有联合变分上界的训练扩散模型Abstract 从离散集合的不可处理分布中进行采样,而不依赖相应的训练数据…...

Web前端开发
首先打开,VS code新建文件夹,命名为index.HTML,然后先对内容进行输入,也就是在波蒂里面进行输入,将社会主义核心价值观的基本内容输入好,然后在页面呈现的效果是这样的 因为有一个alert警告框标签ÿ…...

transformer模型进行英译汉,汉译英
上面是在测试集上的表现 下面是在训练集上的表现 上面是在训练集上的评估效果 这是在测试集上的评估效果,模型是transformer模型,模型应该没问题,以上的是一个源序列没加结束符和加了结束符的情况。 transformer源序列做遮挡填充的自注意力,这就让编码器的输出中每个token的语…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
