概率论原理精解【13】
文章目录
- 在度量空间中,连续映射
- 概述
- 一、度量空间与距离函数
- 二、连续映射的定义
- 三、连续映射的等价定义
- 四、连续映射的性质
- 五、应用与例子
- 球形邻域刻画
- 一、球形邻域的定义
- 二、连续映射的球形邻域刻画
- 三、等价性证明
- 四、应用与例子
- 将度量空间上的连续映射推广到拓扑空间
- 一、拓扑空间的基本概念
- 二、连续映射在拓扑空间中的定义
- 三、从度量空间到拓扑空间的推广
- 四、例子
- 参考文献
- 参考文献
在度量空间中,连续映射
概述
连续映射(或称连续函数)是一个基本概念,它描述了函数在度量空间之间的性质,使得当输入点的距离很小时,输出点的距离也很小。以下是关于度量空间中连续映射的详细解释:
一、度量空间与距离函数
-
度量空间:一个度量空间是一个集合 X X X,配备了一个距离函数(或称度量) d : X × X → R d: X \times X \to \mathbb{R} d:X×X→R,满足以下三个条件:
- 非负性:对于所有 x , y ∈ X x, y \in X x,y∈X,有 d ( x , y ) ≥ 0 d(x, y) \geq 0 d(x,y)≥0,且 d ( x , y ) = 0 d(x, y) = 0 d(x,y)=0当且仅当 x = y x = y x=y。
- 对称性:对于所有 x , y ∈ X x, y \in X x,y∈X,有 d ( x , y ) = d ( y , x ) d(x, y) = d(y, x) d(x,y)=d(y,x)。
- 三角不等式:对于所有 x , y , z ∈ X x, y, z \in X x,y,z∈X,有 d ( x , z ) ≤ d ( x , y ) + d ( y , z ) d(x, z) \leq d(x, y) + d(y, z) d(x,z)≤d(x,y)+d(y,z)。
-
例子:实数集 R \mathbb{R} R配备通常的绝对值距离 d ( x , y ) = ∣ x − y ∣ d(x, y) = |x - y| d(x,y)=∣x−y∣是一个度量空间。
二、连续映射的定义
设 X X X和 Y Y Y是两个度量空间,配备的距离函数分别为 d X d_X dX和 d Y d_Y dY。 一个函数 f : X → Y f: X \to Y f:X→Y被称为是连续的,如果对于 X X X中的任意一点 x x x和任意正实数 ϵ \epsilon ϵ,都存在一个正实数 δ \delta δ,使得当 d X ( x , y ) < δ d_X(x, y) < \delta dX(x,y)<δ时,有 d Y ( f ( x ) , f ( y ) ) < ϵ d_Y(f(x), f(y)) < \epsilon dY(f(x),f(y))<ϵ。
三、连续映射的等价定义
连续映射的定义可以通过不同的方式表述,以下是几种等价的定义:
-
序列连续性:函数 f : X → Y f: X \to Y f:X→Y是连续的,当且仅当对于 X X X中的任意收敛序列 ( x n ) n ∈ N (x_n)_{n \in \mathbb{N}} (xn)n∈N,其像序列 ( f ( x n ) ) n ∈ N (f(x_n))_{n \in \mathbb{N}} (f(xn))n∈N在 Y Y Y中也收敛,并且 lim n → ∞ f ( x n ) = f ( lim n → ∞ x n ) \lim_{n \to \infty} f(x_n) = f(\lim_{n \to \infty} x_n) limn→∞f(xn)=f(limn→∞xn)。
-
邻域连续性:函数 f : X → Y f: X \to Y f:X→Y是连续的,当且仅当对于 Y Y Y中的任意开集 U U U,其逆像 f − 1 ( U ) f^{-1}(U) f−1(U)是 X X X中的开集。
-
闭集连续性:函数 f : X → Y f: X \to Y f:X→Y是连续的,当且仅当对于 Y Y Y中的任意闭集 C C C,其逆像 f − 1 ( C ) f^{-1}(C) f−1(C)是 X X X中的闭集(这一性质在度量空间中成立,但在更一般的拓扑空间中不一定成立)。
四、连续映射的性质
-
复合连续性:如果 f : X → Y f: X \to Y f:X→Y和 g : Y → Z g: Y \to Z g:Y→Z都是连续的,那么复合函数 g ∘ f : X → Z g \circ f: X \to Z g∘f:X→Z也是连续的。
-
常值函数连续性:对于任意度量空间 X X X和 Y Y Y,常值函数 f : X → Y f: X \to Y f:X→Y, f ( x ) = c f(x) = c f(x)=c(其中 c ∈ Y c \in Y c∈Y是常数)是连续的。
-
线性函数连续性:在有限维的实或复向量空间中,配备通常的欧几里得距离或范数距离,线性函数和线性算子都是连续的。
五、应用与例子
-
实分析中的连续函数:在实数集上配备通常的绝对值距离,连续函数的概念与实分析中的连续函数概念一致。
-
拓扑学中的连续映射:连续映射是拓扑学中的基本概念,度量空间中的连续映射是拓扑空间中连续映射的特例。
-
函数空间与算子理论:在函数空间(如 C [ a , b ] C[a, b] C[a,b]或 L p L^p Lp空间)中,连续线性算子(如积分算子、微分算子等)的研究是泛函分析的重要内容。
球形邻域刻画
在度量空间中,连续映射可以通过球形邻域进行刻画。这种刻画方式提供了一种直观且具体的方式来理解连续性的概念。以下是关于度量空间中连续映射的球形邻域刻画的详细解释:
一、球形邻域的定义
在度量空间 X X X中,以点 x ∈ X x \in X x∈X为中心,半径为 r > 0 r > 0 r>0的球形邻域(或称开球)定义为:
B r ( x ) = { y ∈ X ∣ d ( x , y ) < r } B_r(x) = \{ y \in X | d(x, y) < r \} Br(x)={y∈X∣d(x,y)<r}
其中, d d d是度量空间 X X X上的距离函数。
二、连续映射的球形邻域刻画
设 X X X和 Y Y Y是两个度量空间,配备的距离函数分别为 d X d_X dX和 d Y d_Y dY。一个函数 f : X → Y f: X \to Y f:X→Y被称为是连续的,如果对于 X X X中的任意一点 x x x和任意正实数 ϵ \epsilon ϵ,都存在一个正实数 δ \delta δ,使得当 y ∈ B δ ( x ) y \in B_\delta(x) y∈Bδ(x)时,有 f ( y ) ∈ B ϵ ( f ( x ) ) f(y) \in B_\epsilon(f(x)) f(y)∈Bϵ(f(x))。
换句话说,对于 X X X中 x x x的任意一个足够小的球形邻域 B δ ( x ) B_\delta(x) Bδ(x),其像 f ( B δ ( x ) ) f(B_\delta(x)) f(Bδ(x))在 Y Y Y中也是 f ( x ) f(x) f(x)的一个足够小的球形邻域 B ϵ ( f ( x ) ) B_\epsilon(f(x)) Bϵ(f(x))的子集。
三、等价性证明
要证明这种球形邻域刻画与连续映射的通常定义是等价的,我们可以按照以下步骤进行:
-
通常定义到球形邻域刻画的转换:
假设 f f f按通常定义是连续的。对于任意 x ∈ X x \in X x∈X和 ϵ > 0 \epsilon > 0 ϵ>0,由连续性定义,存在 δ > 0 \delta > 0 δ>0,使得当 d X ( x , y ) < δ d_X(x, y) < \delta dX(x,y)<δ时,有 d Y ( f ( x ) , f ( y ) ) < ϵ d_Y(f(x), f(y)) < \epsilon dY(f(x),f(y))<ϵ。这正是球形邻域刻画的要求。 -
球形邻域刻画到通常定义的转换:
假设 f f f按球形邻域刻画是连续的。对于任意 x ∈ X x \in X x∈X和 ϵ > 0 \epsilon > 0 ϵ>0,存在 δ > 0 \delta > 0 δ>0,使得当 y ∈ B δ ( x ) y \in B_\delta(x) y∈Bδ(x)时,有 f ( y ) ∈ B ϵ ( f ( x ) ) f(y) \in B_\epsilon(f(x)) f(y)∈Bϵ(f(x))。即当 d X ( x , y ) < δ d_X(x, y) < \delta dX(x,y)<δ时,有 d Y ( f ( x ) , f ( y ) ) < ϵ d_Y(f(x), f(y)) < \epsilon dY(f(x),f(y))<ϵ。这正是通常定义的要求。
四、应用与例子
-
实数轴上的连续函数:
在实数轴上,配备通常的绝对值距离,连续函数的球形邻域刻画与通常的连续函数定义一致。例如,函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2在实数轴上是连续的,因为对于任意 x ∈ R x \in \mathbb{R} x∈R和 ϵ > 0 \epsilon > 0 ϵ>0,我们可以找到 δ = ϵ \delta = \sqrt{\epsilon} δ=ϵ,使得当 ∣ x − y ∣ < δ |x - y| < \delta ∣x−y∣<δ时,有 ∣ f ( x ) − f ( y ) ∣ = ∣ x 2 − y 2 ∣ = ∣ x − y ∣ ∣ x + y ∣ < ϵ |f(x) - f(y)| = |x^2 - y^2| = |x - y||x + y| < \epsilon ∣f(x)−f(y)∣=∣x2−y2∣=∣x−y∣∣x+y∣<ϵ(这里假设了 x x x和 y y y足够接近,使得 ∣ x + y ∣ |x + y| ∣x+y∣不会太大)。 -
高维空间中的连续映射:
在高维欧几里得空间中,连续映射的球形邻域刻画同样适用。例如,线性映射(如矩阵乘法)在高维空间中通常是连续的,因为对于任意小的输入球形邻域,其输出也是一个小的球形邻域(这可以通过线性映射的保距性或范数性质来证明)。
综上所述,度量空间中的连续映射可以通过球形邻域进行刻画,这种刻画方式提供了一种直观且具体的理解连续性的方法,并且与连续映射的通常定义是等价的。
将度量空间上的连续映射推广到拓扑空间
一、拓扑空间的基本概念
-
拓扑空间:一个拓扑空间是一个集合 X X X,配备了一个称为拓扑的 τ \tau τ(是 X X X的子集族),满足以下三个条件:
- 空集 ∅ \emptyset ∅和全集 X X X都属于 τ \tau τ。
- τ \tau τ中任意多个元素的并集仍属于 τ \tau τ。
- τ \tau τ中有限多个元素的交集仍属于 τ \tau τ。
-
开集:拓扑空间 X X X中的元素(即 X X X的子集)称为开集,如果它属于拓扑 τ \tau τ。
-
闭集:拓扑空间 X X X中的子集称为闭集,如果它的补集是开集。
二、连续映射在拓扑空间中的定义
设 X X X和 Y Y Y是两个拓扑空间,配备的拓扑分别为 τ X \tau_X τX和 τ Y \tau_Y τY。一个函数 f : X → Y f: X \to Y f:X→Y被称为是连续的,如果对于 Y Y Y中的每一个开集 U U U,其逆像 f − 1 ( U ) f^{-1}(U) f−1(U)是 X X X中的一个开集。
三、从度量空间到拓扑空间的推广
在度量空间中,连续映射是通过球形邻域(或开球)来刻画的。然而,在拓扑空间中,我们没有距离的概念,因此不能直接使用球形邻域。但是,我们可以利用开集来模拟球形邻域的作用。
-
开集的作用:在拓扑空间中,开集是描述连续性的基本工具。一个函数在某点是连续的,当且仅当该点附近的所有开集的逆像都是开集。
-
逆像的性质:对于任意集合 A ⊆ Y A \subseteq Y A⊆Y,函数 f f f的逆像 f − 1 ( A ) f^{-1}(A) f−1(A)定义为 { x ∈ X ∣ f ( x ) ∈ A } \{ x \in X | f(x) \in A \} {x∈X∣f(x)∈A}。如果 A A A是开集,那么连续函数 f f f要求 f − 1 ( A ) f^{-1}(A) f−1(A)也是开集。
-
连续性的等价条件:在拓扑空间中,函数 f : X → Y f: X \to Y f:X→Y是连续的,当且仅当对于 X X X中的每一个点 x x x和 Y Y Y中包含 f ( x ) f(x) f(x)的每一个开集 U U U,都存在一个 X X X中包含 x x x的开集 V V V,使得 f ( V ) ⊆ U f(V) \subseteq U f(V)⊆U。这个条件可以看作是度量空间中球形邻域刻画的拓扑版本。
四、例子
-
实数轴上的拓扑:实数轴 R \mathbb{R} R可以配备通常的拓扑,即所有开区间和它们的并集构成的拓扑。在这个拓扑下,连续函数就是通常意义上的连续函数。
-
离散拓扑:对于任意集合 X X X,我们可以定义离散拓扑,即 X X X的所有子集都是开集的拓扑。在这个拓扑下,任意函数都是连续的,因为任意集合的逆像都是开集。
-
不可分拓扑:对于任意集合 X X X(至少包含两个元素),我们可以定义不可分拓扑,即只有空集和全集是开集的拓扑。在这个拓扑下,只有常数函数是连续的。
通过以上推广,我们可以看到连续映射的概念在拓扑空间中得到了更一般的表述,不再依赖于具体的距离或度量。这种推广使得我们能够研究更广泛的数学对象和它们之间的连续关系。
参考文献
参考文献
1.文心一言
2.《测度论基础与高等概率论》
3.ChatGPT
相关文章:

概率论原理精解【13】
文章目录 在度量空间中,连续映射概述一、度量空间与距离函数二、连续映射的定义三、连续映射的等价定义四、连续映射的性质五、应用与例子 球形邻域刻画一、球形邻域的定义二、连续映射的球形邻域刻画三、等价性证明四、应用与例子 将度量空间上的连续映射推广到拓扑…...

年度巨献 | OpenCSG开源最大中文合成数据集Chinese Cosmopedia
01 背景 近年来,生成式语言模型(GLM)的飞速发展正在重塑人工智能领域,尤其是在自然语言处理、内容创作和智能客服等领域展现出巨大潜力。然而,大多数领先的语言模型主要依赖于英文数据集进行训练,中文数据…...

Mac 上,终端如何开启 proxy
文章目录 为什么要这么做前提步骤查看 port查看代理的port配置 bash测试 为什么要这么做 mac 上的终端比较孤僻吧,虽然开了,但是终端并不走🪜…产生的现象就是,浏览器可以访问🌍,但是终端不可以访问&#…...

Linux中的进程入门
冯诺依曼体系结构 操作系统(Operator System) 进程控制块(PCB) struct task_struct{//该进程的所有属性//该进程对应的代码和属性地址struct task_struct* next; }; struct task_struct 内核结构体——>创建内核结构体对象(task_struct)…...

Redis面试真题总结(三)
文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 什么是缓存雪崩?该如何解决? 缓存雪崩是指…...
:大疆)
ARM/Linux嵌入式面经(三三):大疆
嵌入式工程师考察主要蕴含:C/C++,处理器的架构,操作系统(linux或嵌入式实时操作系统),常见硬件接口协议/总线,文件存储系统等几方面 文章目录 1)C/C++static作用,变量加入static以后在内存中存储位置的变化。static的作用变量加入static后在内存中存储位置的变化面试官…...

《DevOps实践指南》笔记-Part 2
一篇文章显得略长,本文对应第3-4章。前言、第1-2章请参考Part 1;第5-6章、附录、认证考试、参考资源等内容,请参考Part 3。 流动的技术实践 持续交付:降低在生产环境中部署和发布变更的风险。包括:打好自动化部署流水…...

树莓派智能语音助手实现音乐播放
树莓派语音助手从诞生的第一天开始,我就想着让它能像小爱音箱一样,可以语音控制播放音乐。经过这些日子的倒腾,今天终于实现了。 接下里,和大家分享下我的实现方法:首先音乐播放模块用的是我在上一篇博文写的《用sound…...

【sgCreateCallAPIFunctionParam】自定义小工具:敏捷开发→调用接口方法参数生成工具
<template><div :class"$options.name" class"sgDevTool"><sgHead /><div class"sg-container"><div class"sg-start"><div style"margin-bottom: 10px">参数列表[逗号模式]<el-too…...
完整版:NacosDocker 安装
第一步:先直接通过命令安装 Nacos docker run --name nacos2.2.3 -d -p 8848:8848 -e MODEstandalone f151dab7a111 第二步:创建 Docker 挂载目录 # 创建 log 目录 mkdir -p /root/nacos 第三步:将 Docker 容器的文件复制到挂载目录中 …...

mysql RR是否会导致幻读?
除了rr级别的当前读,都会幻读 mysql不同隔离级别: 而对于RC级别的语句级快照和RR级别的事务级快照的之间的区别,其实是由read_view生成的时机来实现的。 RC级别在执行语句时,会先关闭原来的read_view,重新生成新的r…...

一篇进阶Python深入理解函数之高阶函数与函数式编程
当我们深入探讨了函数的作用域与闭包,了解到函数不仅是代码的执行单元,还能通过闭包完成数据的封装与保护.接下来,我们将进一步挖掘函数的强大特性,尤其是高阶函数与函数式编程,帮助你更全面地理解 Python 中函数的特性与应用. 高阶函数 高阶函数是指接受一个或多个函数作为参…...

python中Web开发框架的使用
Python 的 Web 开发框架种类繁多,常见的有 Django 和 Flask 这两个框架。它们各有优点,适合不同类型的 Web 应用开发需求。下面,我将详细介绍这两大主流框架的使用方法,让你快速上手 Python 的 Web 开发。 1. Django Django 是一…...

【AI视频】Runway:Gen-2 运镜详解
博客主页: [小ᶻZ࿆] 本文专栏: AI视频 | Runway 文章目录 💯前言💯Camera Control(运镜)💯Camera Control功能测试Horizonta(左右平移)Vertical(上下平移࿰…...

Python “函数” ——Python面试100道实战题目练习,巩固知识、检查技术、成功就业
本文主要是作为Python中函数的一些题目,方便学习完Python的函数之后进行一些知识检验,感兴趣的小伙伴可以试一试,含选择题、判断题、实战题、填空题,答案在第五章。 在做题之前可以先学习或者温习一下Python的函数,推荐…...

[产品管理-15]:NPDP新产品开发 - 13 - 产品创新流程 - 具体产品的创新流程:精益生产与敏捷开发
目录 前言: 一、集成产品开发IPD模型——集成跨功能团队的产品开发 1.1 概述 1、IPD模型的核心思想 2、IPD模型的主要组成部分 3、IPD模型的实施步骤 4、IPD模型的优点 1.2 基于IPD系统的组织实践等级 1.3 IPD的优缺点 二、瀑布开发模型 1、定义与特点…...
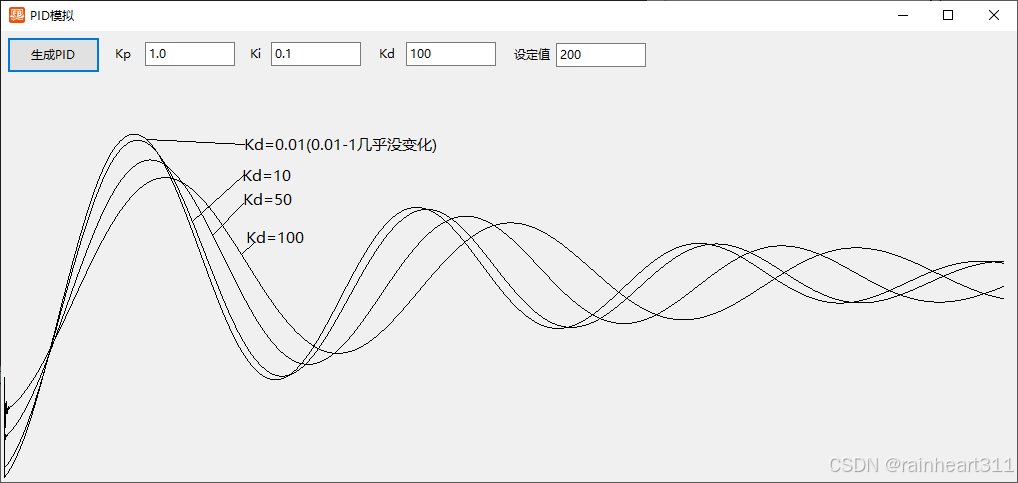
FB仿真模拟PID曲线数据
为了能直观的理解PID的参数调整与曲线数据的变化关系,使用FB写了一个模拟PID曲线数据的程序。 PID类如下: Type PIDController Private : kp_ As Double //比例增益 ki_ As Double //积分增益 kd_ As Double …...

【变化检测】基于ChangeStar建筑物(LEVIR-CD)变化检测实战及ONNX推理
主要内容如下: 1、LEVIR-CD数据集介绍及下载 2、运行环境安装 3、ChangeStar模型训练与预测 4、Onnx运行及可视化 运行环境:Python3.8,torch1.12.0cu113,onnxruntime-gpu1.12.0 likyoo变化检测源码:https://github.c…...

kafka动态认证 自定义认证 安全认证-亲测成功
kafka动态认证 自定义认证 安全认证-亲测成功 背景 Kafka默认是没有安全机制的,一直在裸奔。用户认证功能,是一个成熟组件不可或缺的功能。在0.9版本以前kafka是没有用户认证模块的(或者说只有SSL),好在kafka0.9版本…...

航空航司reese84逆向
reese84逆向 Reese84 是一种用于保护网站防止自动化爬虫抓取的防护机制,尤其是在航空公司网站等需要严格保护数据的平台上广泛使用。这种机制通过复杂的指纹识别和行为分析技术来检测和阻止非人类的互动。例如,Reese84 可以通过分析访问者的浏览器指纹、…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
