信息安全数学基础(15)欧拉定理
前言
欧拉定理是数论中的一个重要定理,它建立了模运算下指数与模的互质关系。这个定理在密码学、信息安全等领域有着广泛的应用,特别是在公钥密码体制(如RSA加密算法)中。
一、表述
设 n 是一个正整数,a 是一个与 n 互质的整数(即 gcd(a,n)=1),那么 (n)≡1(modn),其中 φ(n) 是欧拉函数,表示小于 n 且与 n 互质的正整数的个数。
二、定义
欧拉函数 φ(n) 的定义是:对于任意正整数 n,φ(n) 是小于或等于 n 的正整数中与 n 互质的数的数目。例如,φ(1)=1,φ(2)=1,φ(3)=2,φ(4)=2,φ(5)=4(注意这里 φ(5) 应该是 4 的一个笔误,应为 φ(5)=4−1=1,因为小于 5 且与 5 互质的数只有 1)。
三、证明概要
构造集合:考虑集合 A={a,2a,3a,…,(n−1)a},其中所有元素均对 n 取模。
互质性质:由于 a 与 n 互质,可以证明集合 A 中的元素模 n 后两两不同,且都与 n 互质。
重新排列:将集合 A 中的元素重新排列,使得每个元素都对应到小于 n 且与 n 互质的一个数。这样,我们可以得到一个新的集合 B,其中包含了所有小于 n 且与 n 互质的数。
乘积相等:考虑 A 和 B 中元素的乘积。一方面,A 中元素的乘积是 aφ(n)(n−1)!(模 n);另一方面,B 中元素的乘积是 φ(n)!×(与n互质的数的某个排列)。由于两者模 n 相等,且 φ(n)! 与 n 互质(因为 φ(n)! 只包含小于 n 的质数因子),可以推出 aφ(n)≡1(modn)。
四、应用
欧拉定理在密码学中有着广泛的应用,特别是在RSA加密算法中,它用于证明公钥和私钥的正确性。此外,欧拉定理也是许多数论问题和算法(如中国剩余定理、费马小定理的推广等)的基础。
![]() 结语
结语
困难是纸老虎,你强它就弱
用坚定的信念和不懈的努力
去征服每一个看似不可能的难关
!!!

相关文章:

信息安全数学基础(15)欧拉定理
前言 欧拉定理是数论中的一个重要定理,它建立了模运算下指数与模的互质关系。这个定理在密码学、信息安全等领域有着广泛的应用,特别是在公钥密码体制(如RSA加密算法)中。 一、表述 设 n 是一个正整数,a 是一个与 n 互…...
 command)
sar(1) command
文章目录 1.简介2.格式3.选项4.示例参考文献 1.简介 sar(System Activity Report)收集、报告或保存系统活动信息。 sar 是一个用于监控和报告系统性能的命令行工具。它是 sysstat 套件的一部分,能够收集和报告各种系统活动的信息࿰…...

掌握 JavaScript 中的函数表达式
函数表达式是 javascript 中定义函数的一种方式。与函数声明不同,函数表达式可以是匿名的,并且通常用于将函数视为值的情况。在本文中,我们将探讨函数表达式、如何将函数视为值、回调函数以及函数表达式和函数声明之间的差异。 函数表达式 …...

OpenGL 原生库6 坐标系统
概述 为了将坐标从一个坐标系变换到另一个坐标系,我们需要用到几个变换矩阵,最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。我们的顶点坐标起始于局部空间(Local Space),在这里它称为局部坐标(Local Coordinate)&a…...
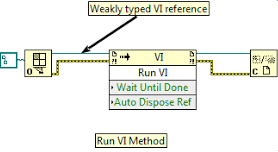
LabVIEW提高开发效率技巧----VI服务器和动态调用
VI服务器(VI Server)和动态调用是LabVIEW中的两个重要功能,可以有效提升程序的灵活性、模块化和可扩展性。通过这两者的结合,开发者可以在运行时动态加载和调用VI(虚拟仪器),实现更为复杂的应用…...

求1000以内所有恰好能分解成10组两个素数之和
要求 根据哥德巴赫猜想,任意一个大偶数都可以分解为两个素数之和。但许多偶数分解为两个素数之和并不是唯一的。 请编写函数fun,其功能是:求1000(不包括1000)以内的所有恰好能分解成10组两个素数之和(5109和1095被认为是同一组)的偶并依次存入数组a中并…...

Webpack 和 Vite 的区别
Webpack 是一种模块打包工具,主要功能是将各种资源(如 JavaScript、CSS、图片等)通过 loader 和 plugin 转换和打包成可以直接在浏览器中运行的代码。其核心思想是以代码分割、按需加载和优化资源来提升性能。 Vite 是一种新型构建工具&…...

C++——初步认识C++和namespace的用法
1.编程语言排行榜 我们通过排行可以看出 C在变成语言中还是占据着重要的地位 2.C在工作领域中的应用 1.PC客户端开发。⼀般是开发Windows上的桌面软件,比如WPS之类的,技术栈的话⼀般是C和 QT,QT 是⼀个跨平台的 C图形用户界面(G…...

LeetCode118:杨辉三角
题目链接:118. 杨辉三角 - 力扣(LeetCode) 代码如下 class Solution {public:vector<vector<int>> generate(int numRows) {vector<vector<int>> dp(numRows);vector<int> temp(numRows);for (int i 0; i &…...

介绍一下大模型或者多模态?
什么是大模型、多模态 大模型多模态 大模型 定义: 大模型,通常指的是在深度学习领域,具有大规模参数和复杂结构的模型。这些模型往往需要大量的计算资源和数据进行训练和推理。大模型因其强大的表示能力和泛化性能,在多个领域展现…...

深度学习之图像数据集增强(Data Augmentation)
文章目录 一、 数据增强概述二、python实现传统数据增强参考文献 一、 数据增强概述 数据增强(Data Augmentation)是一种技术,通过对现有数据进行各种变换和处理来生成新的训练样本,从而增加数据集的多样性和数量。这些变换可以是…...

小程序与APP的区别
目录 前言1. 开发方式与成本2. 运行环境与获取途径3. 功能复杂度与交互体验4. 更新与维护5. 推广与用户获取6. 占用空间与存储7. 可分享性总结 前言 小程序与APP作为两种不同类型的应用程序,它们在多个方面存在明显的区别。以下是对这些区别的详细阐述:…...

Linux Kernel Makefiles 编译标志详解
在Linux内核开发中,Makefile文件扮演着至关重要的角色,它指导make命令如何编译和链接内核源代码。Makefile中包含了多种编译标志(flags),这些标志控制着编译、汇编和链接过程的不同方面。本文将详细介绍几种关键的编译…...

数据可视化pyecharts——数据分析(柱状图、折线图、饼图)
安装 首先确保已经安装了pyecharts库,如果没有,可以通过pip install pyecharts进行安装。 柱状图 从pyecharts.charts导入Bar,从pyecharts导入options。准备数据(如类别数据x_data和对应的数值数据y_data)。创建Bar对…...

小程序构建npm失败
小程序构建npm失败 项目工程结构说明解决方法引入依赖导致的其他问题 今天在初始化后的小程序中引入TDesign组件库,构建npm时报错。 项目工程结构说明 初始化后的项目中,包含miniprogram文件夹和一些项目配置文件,在project.config.json文件中…...

计算机人工智能前沿进展-大语言模型方向-2024-09-20
计算机人工智能前沿进展-大语言模型方向-2024-09-20 1. Multimodal Fusion with LLMs for Engagement Prediction in Natural Conversation Authors: Cheng Charles Ma, Kevin Hyekang Joo, Alexandria K. Vail, Sunreeta Bhattacharya, Alvaro Fern’andez Garc’ia, Kailan…...

cv环境设置
pytorch TensorFlow。。。 环境布置,库的安装顺序: 确定显卡可用的cuda上下限 (比如3090需要至少11.x以上的cuda参考: 一文理顺:pytorch、cuda版本,从此不再为兼容问题头疼! - 哔哩哔哩 (bilibili.com)&am…...

线性代数书中求解线性方程组的三种方法的实例
目录 一、克拉默法则(P45) 二、逆矩阵(P46) 三、高斯-约旦消元法(P65) 一、克拉默法则(P45) 二、逆矩阵(P46) 三、高斯-约旦消元法(P65)...

Linux容器化管理——Docker常见命令总结
创建镜像 docker build -t (镜像名) . 自动在当前目录下找dockerfile也可换成其他路径 查看本地镜像 docker images 登陆镜像服务器 docker login -u (登录名) -p (登陆密码) (镜像服务器…...
智慧校园建设解决方案建设系统简介
一、建设背景 1.1 政策背景 1.2 班牌的演变 1.3 建设愿景 二、 智慧班牌简介 三、智慧班牌系统 3.1 系统概述 3.2 软件平台功能交互简介 3.2.1 智慧班牌与管理平台间的功能关联 3.2.2 手机客户端(管理员、教师、家长端) 3.2.3 手机客户端&#x…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
