回溯算法总结篇
组合问题:N个数里面按一定规则找出k个数的集合
如果题目要求的是组合的具体信息,则只能使用回溯算法,如果题目只是要求组合的某些最值,个数等信息,则使用动态规划(比如求组合中元素最少的组合,求组合的个数等)
77. 组合
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {dfs(1, n, k);return res;
}private void dfs(int start, int n, int k) {if (path.size() == k) {res.add(new ArrayList<>(path));return;}// for循环的作用,固定第一个值,比如 1~4,分别固定1~4,如果start为2,则不会遍历到1for (int i = start; i <= n; i++) {path.push(i); // 记录dfs(i + 1, n, k);path.pop(); // 回溯}
}39. 组合总和
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {dfs(0, candidates, target);return res;
}private void dfs(int start, int[] candidates, int target) {// 如果target为0,说明找到解if (0 == target) {res.add(new ArrayList<>(path));return;}for (int i = start; i < candidates.length; i++) {int candidate = candidates[i];if (target < candidate) {continue; // 剪枝}path.push(candidate);dfs(i, candidates, target - candidate); // // 关键点:不用i+1了,表示可以重复读取当前的数path.pop();}
}40. 组合总和 II
List<List<Integer>> result = new LinkedList<>();
LinkedList<Integer> stack = new LinkedList<>();
boolean[] visited;public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates); // 排序,将相同的元素相邻放置visited = new boolean[candidates.length];dfs(0, candidates, target);return result;
}public void dfs(int start, int[] candidates, int target) {if (target == 0) {result.add(new LinkedList<>(stack));return;}for (int i = start; i < candidates.length; i++) {int candidate = candidates[i];if (target < candidate) {continue; // 减枝}// 如果相邻的两个值相等,且前一个值还没有被访问,则跳过循环// (相邻的值只有一个可以被先访问,防止组合结果出现重复)比如:【521,512】if (i > 0 && candidate == candidates[i - 1] && !visited[i - 1]) {continue;}visited[i] = true;stack.push(candidate);// 不同点,从当前遍历到的元素后面开始递归,start = i+1;排除自身(使得结果中一个元素只能出现一次)dfs(i + 1, candidates, target - candidate);stack.pop();visited[i] = false;}
}216. 组合总和 III
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum3(int k, int n) {dfs(1, k, n);return res;
}private void dfs(int start, int k, int target) {if (target == 0 && path.size() == k) {res.add(new ArrayList<>(path));return;}for (int i = start; i <= 9; i++) {if (target < i) {continue; // 剪枝}if (path.size() == k) {continue; // 剪枝}path.push(i);dfs(i + 1, k, target - i);path.pop();}
}17. 电话号码的字母组合
List<String> res = new ArrayList<>(); // 存放最终的结果集合
StringBuilder temp = new StringBuilder(); // 每个结果public List<String> letterCombinations(String digits) {if (digits == null || digits.isEmpty()) {return res;}// 数字和字符串的映射关系,比如数组下标为2时,numString[2] == "abc"String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};// 递归dfs(digits, numString, 0);return res;
}/**** @param digits 题目的参数,比如”23”* @param numString 数字和字符串的映射关系* @param i 当前正在处理的字符串的索引 比如0,则表示正在处理 digits的第一个字符串,也是就2对应的字符串‘abc’*/
private void dfs(String digits, String[] numString, int i) {if (digits.length() == temp.length()) {// 将结果加入集合res.add(temp.toString());return;}// 取当前应该处理的字符串// digits.charAt(i)表示取参数中的数字,比如“2” -'0'操作将其转化为2~9范围内的int类型// numString[digits.charAt(i) - '0']; 则表示在映射关系中取当前数字对应的字符串char charAt = digits.charAt(i);String str = numString[charAt - '0'];for (int j = 0; j < str.length(); j++) {temp.append(str.charAt(j));dfs(digits, numString, i + 1); // 取下一个字符串一个一个处理// 比如“digits”为“23”,则先取2对应的字符串“abc”,然后固定'a',递归处理3对应的字符串'def',固定'd',则返回'ad'temp.deleteCharAt(temp.length() - 1);}
}切割问题:一个字符串按一定规则有几种切割方式
在
for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
131. 分割回文串
class Solution {//保持前几题一贯的格式List<List<String>> res = new ArrayList<>();List<String> cur = new ArrayList<>();public List<List<String>> partition(String s) {backtracking(s, 0, new StringBuilder());return res;}private void backtracking(String s, int start, StringBuilder sb) {//因为是起始位置一个一个加的,所以结束时start一定等于s.length,因为进入backtracking时一定末尾也是回文,所以cur是满足条件的if (start == s.length()) {//注意创建一个新的copyres.add(new ArrayList<>(cur));return;}//像前两题一样从前往后搜索,如果发现回文,进入backtracking,起始位置后移一位,循环结束照例移除cur的末位for (int i = start; i < s.length(); i++) {sb.append(s.charAt(i));if (check(sb)) {cur.add(sb.toString());backtracking(s, i + 1, new StringBuilder());cur.remove(cur.size() - 1);}}}//helper method, 检查是否是回文,前后指针指向的元素不同,则不是回文private boolean check(StringBuilder sb) {for (int i = 0; i < sb.length() / 2; i++) {if (sb.charAt(i) != sb.charAt(sb.length() - 1 - i)) {return false;}}return true;}}93. 复原 IP 地址❤️
class Solution {LinkedList<String> res = new LinkedList<>();public List<String> restoreIpAddresses(String s) {if (s.length() > 12) {return res;}backTrack(s, 0, 0);return res;}private void backTrack(String s, int startIndex, int pointNum) {if (pointNum == 3) {if (isValid(s, startIndex, s.length() - 1)) {res.add(s);}return;}for (int i = startIndex; i < s.length(); i++) {if (isValid(s, startIndex, i)) {s = s.substring(0, i + 1) + '.' + s.substring(i + 1);pointNum++;backTrack(s, i + 2, pointNum);pointNum--;s = s.substring(0, i + 1) + s.substring(i + 2);} else {break;}}}/*** 验证当前子串是否符合下面三个条件* 1.子串的第一个字符不为0* 2.子串总数不大于255* 3.子串为正整数*/private boolean isValid(String s, int start, int end) {if (start > end) {return false;}if (s.charAt(start) == '0' && start != end) {return false;}int num = 0;for (int i = start; i <= end; i++) {num = num * 10 + s.charAt(i) - '0';if (num > 255) {return false;}}return true;}}子集问题:一个N个数的集合里有多少符合条件的子集
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
78. 子集❤️
List<List<Integer>> list = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> subsets(int[] nums) {dfs(0, nums);return list;
}private void dfs(int start, int[] nums) {// 子集是收集树形结构中树的所有节点的结果。list.add(new ArrayList<>(path));for (int i = start; i < nums.length; i++) {int num = nums[i];path.push(num);dfs(i + 1, nums);path.pop();}
}90. 子集 II
子集II问题:这种需要回溯解决的题目,组合问题,子集问题,切割问题,如果遇到原先给你的集合中有重复元素,而输出的结果中不允许有重复结果的,需要先将原始数组排序,然后使用一个boolean类型的数组,标记每个元素是否被访问,对于重复的元素,如果前一个元素没有被访问,则不允许访问第二个元素
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
boolean[] used; // 元素是否被访问public List<List<Integer>> subsetsWithDup(int[] nums) {if (nums.length == 0) {result.add(path);return result;}Arrays.sort(nums);used = new boolean[nums.length];dfs(nums, 0);return result;
}private void dfs(int[] nums, int startIndex) {result.add(new ArrayList<>(path));if (startIndex >= nums.length) { // 终止条件return;}for (int i = startIndex; i < nums.length; i++) {// 去重,递归树层去重,如果nums中有重复,则必须先访问前面的元素才能访问后面的元素if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {// 如果出现重复,前面一个还没访问,则跳出循环continue;}int num = nums[i];path.push(num);used[i] = true;dfs(nums, i + 1);path.pop();used[i] = false;}
}491. 非递减子序列
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {dfs(0, nums);return res;
}public void dfs(int start, int[] nums) {if (path.size() > 1) {res.add(new ArrayList<>(path));}// 使用数组去重,第一遇到一个值将对应数组下标置位1,如果再次遇到1,则说明已经访问过,跳过int[] used = new int[201];for (int i = start; i < nums.length; i++) {int num = nums[i];if (!path.isEmpty() && path.get(path.size() - 1) > num ||used[num + 100] == 1) {continue;}used[num + 100] = 1;path.add(num);dfs(i + 1, nums);path.remove(path.size() - 1);}
}排列问题:N个数按一定规则全排列,有几种排列方式
每层都是从0开始搜索而不是startIndex
需要used数组记录path里都放了哪些元素了
46. 全排列❤️❤️
class Solution {List<List<Integer>> res = new LinkedList<>();List<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[nums.length];dfs( nums);return res;}private void dfs(int[] nums) {if (path.size() == nums.length) {res.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if(!used[i]){used[i] =true;path.add(nums[i]);dfs(nums);used[i] = false;path.remove(path.size()-1);}}}
}47. 全排列 II❤️
class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> path = new LinkedList<>();boolean[] used; // 判断一个元素是否被访问public List<List<Integer>> permuteUnique(int[] nums) {used = new boolean[nums.length];// 定义一个集合存放结果/******************************和46的区别*******************************/Arrays.sort(nums); // 排序/******************************和46的区别*******************************/doPermute(nums);return res;}private void doPermute(int[] nums) {if (path.size() == nums.length) {res.add(new LinkedList<>(path));}for (int i = 0; i < nums.length; i++) {/******************************和46的区别*******************************/if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue; // 相邻元素如果相等且前一个元素还没有被处理,则跳过 【两个相邻元素只有一个可以先被处理,排除重复】}/******************************和46的区别*******************************/if (!used[i]) {path.push(nums[i]);used[i] = true;doPermute(nums); // 递归path.pop(); // 回溯used[i] = false; // 回溯}}}
}棋盘问题:N皇后,解数独等等
51. N 皇后
使用三个数组分别标记,列冲突,左斜线冲突,右斜线冲突
根据当前位置的横坐标 X 和纵坐标 Y 计算当前位置所处的左斜线公式:X + Y ,
右斜线公式为 N - 1 - ( X - Y )
class Solution {boolean[] currCol;boolean[] leftSlash;boolean[] rightSlash;char[][] chessBoard;List<List<String>> res = new ArrayList<>();List<String> path = new ArrayList<>();public List<List<String>> solveNQueens(int n) {currCol = new boolean[n]; // 当前列数组大小和N皇后的N的大小相同leftSlash = new boolean[2 * n - 1]; // 左斜线的大小等于2*N-1,因为在N*N大小的棋盘上有2*N-1个对角线rightSlash = new boolean[2 * n - 1]; // 右斜线同理chessBoard = new char[n][n];for (char[] chars : chessBoard) {Arrays.fill(chars, '.');}dfs(0);return res;}private void dfs(int i) {int n = currCol.length;if (i == n) {for (char[] chars : chessBoard) {StringBuilder stringBuilder = new StringBuilder();for (char c : chars) {stringBuilder.append(c);}path.add(stringBuilder.toString());}res.add(new ArrayList<>(path));path.clear();}for (int j = 0; j < n; j++) {if (currCol[j] || leftSlash[i + j] || rightSlash[n - 1 - (i - j)]) {continue;}chessBoard[i][j] = 'Q';currCol[j] = true;leftSlash[i + j] = true;rightSlash[n - 1 - (i - j)] = true;dfs(i + 1);chessBoard[i][j] = '.';currCol[j] = false;leftSlash[i + j] = false;rightSlash[n - 1 - (i - j)] = false;}}
}37. 解数独
解数独问题需要使用三个二维数组记录,行冲突,列冲突,九宫格冲突
根据当前位置的横坐标 X 和纵坐标 Y 计算当前位置所处的九宫格公式为:
X / 3 * 3 + Y / 3
class Solution {boolean[][] ca = new boolean[9][9]; // 行冲突boolean[][] cb = new boolean[9][9];// 列冲突boolean[][] cc = new boolean[9][9];// 九宫格冲突public void solveSudoku(char[][] board) {// 记录当前数独中已经存在的数组for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {char c = board[i][j];if (c != '.') { // 如果字符不为'.'ca[i][c - '1'] = true; // 将其所在行的数字c设置为冲突(该行不能再添加c数字)cb[j][c - '1'] = true; // 将其所在列的数字c设置为冲突(该列不能再添加c数字)cc[i / 3 * 3 + j / 3][c - '1'] = true; // 将其所在九宫格的数字c设置为冲突(该九宫格不能再添加c数字)}}}// 参数一:正在处理的行,参数二:正在处理的列,参数三:整个二维数组dfs(0, 0, board);}private boolean dfs(int i, int j, char[][] board) {// 跳过数独中已经有数字的地方while (board[i][j] != '.') {// 超出列长,则列长恢复为0,行++if (++j >= 9) {j = 0;i++;}// i>=9 说明已经遍历完所有数组中的元素if (i >= 9) {return true;}}// 通过上面的while跳过数独中有数字的地方,找到了没有数字的地方,开始尝试从1~9放入数字for (int x = 1; x <= 9; x++) {// 如果添加的数字x在当前行,当前列,当前九宫格中有任意一个冲突,则跳过,尝试下一个数字if (ca[i][x - 1] || cb[j][x - 1] || cc[i / 3 * 3 + j / 3][x - 1]) {continue;}// 如果没有冲突,向[i,j]节点添加x数字board[i][j] = (char) (x + '0');// 添加完数字后,更新冲突数组,把当前行,当前列,当前九宫格中的x-1设置为trueca[i][x - 1] = cb[j][x - 1] = cc[i / 3 * 3 + j / 3][x - 1] = true;boolean dfs = dfs(i, j, board); // 递归if (dfs) {return true; // 如果找到解,则直接返回true}board[i][j] = '.'; // 如果没找到解,回溯ca[i][x - 1] = cb[j][x - 1] = cc[i / 3 * 3 + j / 3][x - 1] = false; //回溯}return false;}
}相关文章:

回溯算法总结篇
组合问题:N个数里面按一定规则找出k个数的集合 如果题目要求的是组合的具体信息,则只能使用回溯算法,如果题目只是要求组合的某些最值,个数等信息,则使用动态规划(比如求组合中元素最少的组合,…...

机器学习-点击率预估-论文速读-20240916
1. [经典文章] 特征交叉: Factorization Machines, ICDM, 2010 分解机(Factorization Machines) 摘要 本文介绍了一种新的模型类——分解机(FM),它结合了支持向量机(SVM)和分解模型的优点。与…...

【leetcode】堆习题
215.数组中的第K个最大元素 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输…...
和嵌入(Embedding)解析 - llm的输入)
前端大模型入门:编码(Tokenizer)和嵌入(Embedding)解析 - llm的输入
LLM的核心是通过对语言进行建模来生成自然语言输出或理解输入,两个重要的概念在其中发挥关键作用:Tokenizer 和 Embedding。本篇文章将对这两个概念进行入门级介绍,并提供了针对前端的js示例代码,帮助读者理解它们的基本原理/作用和如何使用。 1. 什么是…...

一文读懂 JS 中的 Map 结构
你好,我是沐爸,欢迎点赞、收藏、评论和关注。 上次聊了 Set 数据结构,今天我们聊下 Map,看看它与 Set、与普通对象有什么区别?下面直接进入正题。 一、Set 和 Map 有什么区别? Set 是一个集合࿰…...
)
C++校招面经(二)
欢迎关注 0voice GitHub 6、 C 和 Java 区别(语⾔特性,垃圾回收,应⽤场景等) 指针: Java 语⾔让程序员没法找到指针来直接访问内存,没有指针的概念,并有内存的⾃动管理功能,从⽽…...

Python Web 面试题
1 Web 相关 get 和 post 区别 get: 请求数据在 URL 末尾,URL 长度有限制 请求幂等,即无论请求多少次,服务器响应始终相同,这是因为 get 至少获取资源,而不修改资源 可以被浏览器缓存,以便以后…...

java日志框架之JUL(Logging)
文章目录 一、JUL简介1、JUL组件介绍 二、Logger快速入门三、Logger日志级别1、日志级别2、默认级别info3、原理分析4、自定义日志级别5、日志持久化(保存到磁盘) 三、Logger父子关系四、Logger配置文件 一、JUL简介 JUL全程Java Util Loggingÿ…...

ARM驱动学习之PWM
ARM驱动学习之PWM 1.分析原理图: GPD0_0 XpwmTOUT0定时器0 2.定时器上的资源: 1.5组32位定时器 2.定时器产生内部中断 3.定时器0,1,2可编程实现pwm 4.定时器各自分频 5.TCN--,TCN TCMPBN 6.分频器 24-2 7.24.3.4 例子࿱…...

我的AI工具箱Tauri版-VideoClipMixingCut视频批量混剪
本教程基于自研的AI工具箱Tauri版进行VideoClipMixingCut视频批量混剪。 VideoClipMixingCut视频批量混剪 是自研AI工具箱Tauri版中的一款强大工具,专为自动化视频批量混剪设计。该模块通过将预设的解说文稿与视频素材进行自动拼接生成混剪视频,适合需要…...

postgres_fdw访问存储在外部 PostgreSQL 服务器中的数据
文章目录 一、postgres_fdw 介绍二、安装使用示例三、成本估算四、 远程执行选项执行计划无法递推解决 参考文件: 一、postgres_fdw 介绍 postgres_fdw 模块提供外部数据包装器 postgres_fdw,可用于访问存储在外部 PostgreSQL 服务器中的数据。 此模块…...

什么是3D展厅?有何优势?怎么制作3D展厅?
一、什么是3D展厅? 3D展厅是一种利用三维技术构建的虚拟展示空间。它借助虚拟现实(VR)、增强现实(AR)等现代科技手段,将真实的展示空间数字化,呈现出逼真、立体、沉浸的展示效果。通过3D展厅&a…...
Linux下的CAN通讯
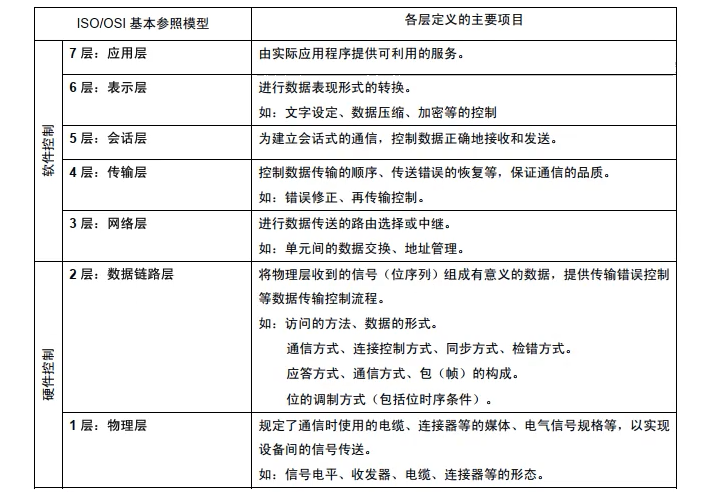
CAN总线 CAN总线简介 CAN(Controller Area Network)总线是一种多主从式 <font color red>异步半双工串行 </font> 通信总线,它最早由Bosch公司开发,用于汽车电子系统。CAN总线具有以下特点: 多主从式&a…...

【Python】pip安装加速:使用国内镜像源
【Python】pip安装加速:使用国内镜像源 零、使用命令行设置 设置全局镜像源 随便使用下面任一命令即可! 阿里云: pip config set global.index-url https://mirrors.aliyun.com/pypi/simple/豆瓣: pip config set global.in…...
)
SpringBoot lombok(注解@Getter @Setter)
SpringBoot lombok(注解Getter Setter) 使用lombok注解的方式,在编译生成的字节码文件中就会存在setter/getter等方法,减少代码量,方便了代码的维护 添加依赖 <dependency><groupId>org.projectlombok</groupId><artif…...

descrTable常用方法
descrTable 为 R 包 compareGroups 的重要函数,有关该函数以及 compareGroups 包的详细内容见:R包compareGroups详细用法 加载包和数据 library(compareGroups)# 加载 REGICOR 数据(横断面,从不同年份纳入,每个变量有…...

回归预测 | Matlab实现ReliefF-XGBoost多变量回归预测
回归预测 | Matlab实现ReliefF-XGBoost多变量回归预测 目录 回归预测 | Matlab实现ReliefF-XGBoost多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.ReliefF-xgboost回归预测代码,对序列数据预测性能相对较高。首先通过ReleifF对输入特征计算权…...

年度最强悬疑美剧重磅回归,一集比一集上头
纽约的夜晚,平静被一声枪响打破,一场离奇的谋杀案悄然上演。《大楼里只有谋杀》正是围绕这样一桩扑朔迷离的案件展开的。三位主角,赛琳娜戈麦斯饰演的梅宝、史蒂夫马丁饰演的查尔斯、马丁肖特饰演的奥利弗,这些性格迥异的邻居因为…...

AI一点通: 简化大数据与深度学习工作流程, Apache Spark、PyTorch 和 Mosaic Streaming
在大数据和机器学习飞速发展的领域中,数据科学家和机器学习工程师经常面临的一个挑战是如何桥接像 Apache Spark 这样的强大数据处理引擎与 PyTorch 等深度学习框架。由于它们在架构上的固有差异,利用这两个系统的优势可能令人望而生畏。本博客介绍了 Mo…...

Python知识点:深入理解Python的模块与包管理
开篇,先说一个好消息,截止到2025年1月1日前,翻到文末找到我,赠送定制版的开题报告和任务书,先到先得!过期不候! 深入理解Python的模块与包管理 Python的模块和包是代码组织、复用和分发的基本…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
