【小波去噪】【matlab】基于小波分析的一维信号滤波(对照组:中值滤波、均值滤波、高斯滤波)
链接1-傅里叶变换
链接2-傅立叶分析和小波分析间的关系
链接3-小波变换(wavelet transform)的通俗解释
链接4-小波基的选择
1.示例代码
function main_wavelet
clc
clear
close all
warning off
%% 1.信号生成
time_length = 10;%总时长,秒
sample_rate = 100;% 采样率,Hz
freq = 10; % 生成的信号的频率,Hz
t = linspace(0, time_length, time_length * sample_rate); % 生成时间轴
signal = 2*sin(2 * pi * freq * t);% 生成正弦信号
noise = 0.5 * randn(size(signal));% 生成白噪声,高斯过程
noisy_signal = signal + noise;% 将正弦信号和噪声信号相加生成含噪采集数据figure(1)
plot(t,signal,'b-')
hold on
plot(t, noisy_signal,'r-');
hold on
plot(t, noise,'k-');
xlabel('Time (s)');
ylabel('Amplitude');
legend('原信号','含噪信号','噪声')% save('noise.mat','noisy_signal')
%% 2.小波变换
% 设置小波函数和变换阶数
wname = 'db4'; % 选用 Daubechies 4 小波
level = 2; % 小波变换的阶数
% 进行小波变换
[C, L] = wavedec(noisy_signal, level, wname);
% 提取细节系数
D = detcoef(C, L, level);
% 对细节系数进行阈值处理
sigma = median(abs(D)) / 0.6745; % 计算阈值,robust estimator估计方法
D = wthresh(D, 'h', sigma); % 硬阈值处理
% 重构信号
data_denoised = wrcoef('a', C, L, wname, level);%% 3.绘制结果
figure(3)
subplot(3,1,1); plot(t, noisy_signal,'b-'); title('原始信号(含噪声)');
subplot(3,1,2); plot(t,signal,'b-'); title('原始信号(无噪声)');
subplot(3,1,3); plot(t,data_denoised,'b-'); title('降噪后的信号');figure(4)
plot(t,signal,'b-')
hold on
plot(t,data_denoised,'r-')
legend('原始信号(无噪声)','降噪后的信号')
2.对比滤波器
作为对比,以下代码直接在第1节的main_wavelet.m之后运行即可
中值滤波、均值滤波、高斯滤波
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 一维中值滤波
n=21; % n为模板长度,值可以改变
y=medfilt1(noisy_signal,n);
figure(101)
plot(t,noisy_signal,'b-')
hold on
plot(t,y,'r-')
legend('中值滤波前的序列','中值滤波后的序列')
%% 一维均值滤波
n=5; % n为模板长度,值可以改变
mean=ones(1,n)./n; % mean为1×n的模板,各数组元素的值均为1/n
y = conv(noisy_signal,mean);
y=y(1:length(y)-length(mean)+1);
figure(102);
plot(t,noisy_signal,'b-')
hold on
plot(t,y,'r-')
legend('均值滤波前的序列','均值滤波后的序列')
%% 一维高斯滤波
gau=[0.0009 0.0175 0.1295 0.3521 0.3521 0.1295 0.0175 0.0009]; % 标准差为1时的高斯函数一维模板,如果标准差不为1,则要修改模板
% gau=[0.0090,0.4910,0.4910,0.0090]; % 标准差为0.5时的高斯函数一维模板,如果标准差不为0.5,则要修改模板
y=conv(noisy_signal,gau);
y=y(1:length(y)-length(gau)+1);
figure(103);
plot(t,noisy_signal,'b-')
hold on
plot(t,y,'r-')
legend('高斯滤波前的序列','高斯滤波后的序列')
3.封装代码
主代码
function wavelet_fun_main240919
clc
clear
close all
warning off
%% 1.信号生成
time_length = 10;%总时长,秒
sample_rate = 100;% 采样率,Hz
freq = 10; % 生成的信号的频率,Hz
t = linspace(0, time_length, time_length * sample_rate); % 生成时间轴
noise = 0.5 * randn(size(t));% 生成白噪声,高斯过程
Results_JGLD_ideal = 2*sin(2 * pi * freq * t);% 生成正弦信号
Results_JGLD_error = Results_JGLD_ideal + noise;% 将正弦信号和噪声信号相加生成含噪采集数据%% 小波降噪处理
dt=1/sample_rate;%采样时间间隔
data_denoised=WaveletGenerate(Results_JGLD_ideal,Results_JGLD_error,dt);%% 画图
figure(1)
plot(t,Results_JGLD_ideal,'b-')
hold on
plot(t,data_denoised,'r-')
legend('原始信号(无噪声)','降噪后的信号')
WaveletGenerate.m
function data_denoised=WaveletGenerate(Results_JGLD_ideal,Results_JGLD_error,dt)
%% 1.信号生成
signal = Results_JGLD_ideal;% 原始信号
noisy_signal = Results_JGLD_error;%含噪采集数据
% dt=0.01;%时间间隔
t=dt:dt:(length(signal))*dt;
%% 2.小波变换
% 设置小波函数和变换阶数
wname = 'db4'; % 选用 Daubechies 4 小波
level = 1; % 小波变换的阶数
% 进行小波变换
[C, L] = wavedec(noisy_signal, level, wname);
% 提取细节系数
D = detcoef(C, L, level);
% 对细节系数进行阈值处理
sigma = median(abs(D)) / 0.6745; % 计算阈值,robust estimator估计方法
D = wthresh(D, 'h', sigma); % 硬阈值处理
% 重构信号
data_denoised = wrcoef('a', C, L, wname, level);相关文章:
)
【小波去噪】【matlab】基于小波分析的一维信号滤波(对照组:中值滤波、均值滤波、高斯滤波)
链接1-傅里叶变换 链接2-傅立叶分析和小波分析间的关系 链接3-小波变换(wavelet transform)的通俗解释 链接4-小波基的选择 1.示例代码 function main_wavelet clc clear close all warning off %% 1.信号生成 time_length 10;%总时长,秒 …...

CentOS 7官方源停服,配置本机光盘yum源
1、挂载系统光盘 mkdir /mnt/iso mount -o loop /tools/CentOS-7-x86_64-DVD-1810.iso /mnt/iso cd /mnt/iso/Packages/ rpm -ivh /mnt/iso/Packages/yum-utils-1.1.31-50.el7.noarch.rpm(图形界面安装,默契已安装) 如安装yum-utils依赖错误&#x…...

2024年汉字小达人区级自由报名备考冲刺:2024官方模拟题练一练(续)
2024年第十一届汉字小达人的区级活动的时间9月25-30日正式开赛,满打满算还有9天时间。 今天继续回答一些问题关于汉字小达人的常见问题,再做几道2024年官方模拟题,帮助大家直观地了解汉字小达人的比赛题型和那你程度。 本专题在比赛前持续更…...

实战Redis与MySQL双写一致性的缓存模式
Redis和MySQL都是常用的数据存储系统,它们各自有自己的优缺点。在实际应用中,我们可能需要将它们结合起来使用,比如将Redis作为缓存,MySQL作为持久化存储。 在这种情况下,我们需要保证Redis和MySQL的数据一致性&…...
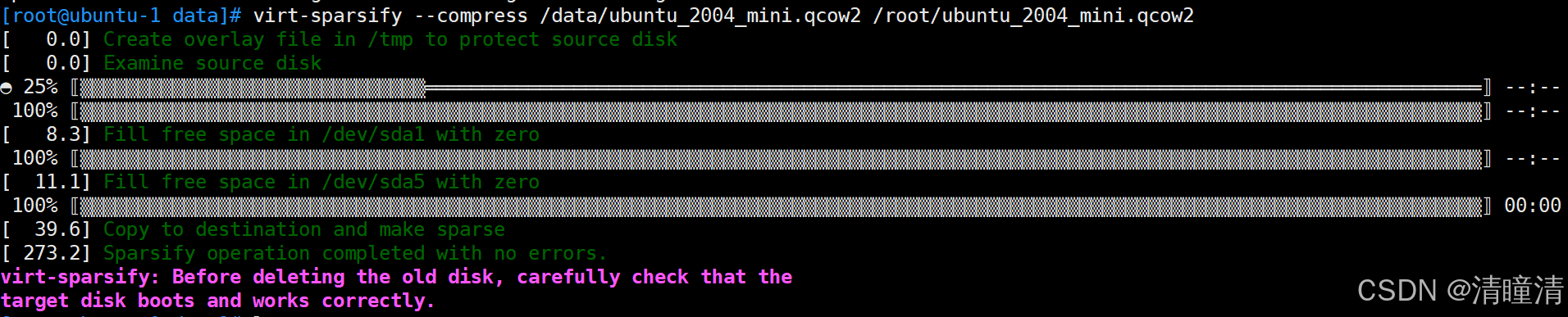
KVM环境下制作ubuntu qcow2格式镜像
如果是Ubuntu KVM环境是VMware虚拟机,需要CPU开启虚拟化 1、配置镜像源 wget -O /etc/apt/sources.list https://www.qingtongqing.cc/ubuntu/sources.list2、安装kvm qemu-img libvirt kvm虚拟化所需环境组件 apt -y install qemu-kvm virt-manager libvirt-da…...

基于SpringBoot+Vue的高校竞赛管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 【2025最新】基于JavaSpringBootVueMySQL的…...

PHP发邮件教程:配置SMTP服务器发送邮件?
PHP发邮件的几种方式?如何使用PHP通过SMTP协议发信? PHP作为一种广泛使用的服务器端脚本语言,提供了多种方式来发送邮件。AokSend将详细介绍如何通过配置SMTP服务器来实现PHP发邮件教程的核心内容。 PHP发邮件教程:设置参数 这…...

SpringBootWeb增删改查入门案例
前言 为了快速入门一个SpringBootWeb项目,这里就将基础的增删改查的案例进行总结,作为对SpringBootMybatis的基础用法的一个巩固。 准备工作 需求说明 对员工表进行增删改查操作环境搭建 准备数据表 -- 员工管理(带约束) create table emp (id int …...

pytorch实现RNN网络
目录 1.导包 2. 加载本地文本数据 3.构建循环神经网络层 4.初始化隐藏状态state 5.创建随机的数据,检测一下代码是否能正常运行 6. 构建一个完整的循环神经网络 7.模型训练 8.个人知识点理解 1.导包 import torch from torch import nn from torch.nn imp…...

智能工厂的软件设计 “程序program”表达式,即 接口模型的代理模式表达式
Q1、前面将“智能工厂的软件设计”中绝无仅有的“程序”视为 专注于 给定的某个单一面(语言面/逻辑面/数学面)中的 问题,专注于分析问题和解决问题的程序活动的组织,每一面都是一个“组织者”就像一个“独角兽”,并提出…...

leetcode 难度【简单模式】标签【数据库】题型整理大全
文章目录 175. 组合两个表181. 超过经理收入的员工182. 查找重复的电子邮箱COUNT(*)COUNT(*) 与 COUNT(column) 的区别 where和vaing之间的区别用法 183.从不订购的客户196.删除重复的电子邮箱197.上升的温度511.游戏玩法分析I512.游戏玩法分析II577.员工奖金584.寻找用户推荐人…...

利士策分享,自我和解:通往赚钱与内心富足的和谐之道
利士策分享,自我和解:通往赚钱与内心富足的和谐之道 在这个快节奏、高压力的时代,我们往往在追求物质财富的同时,忽略了内心世界的和谐与平衡。 赚钱,作为现代生活中不可或缺的一部分,它不仅仅是生存的手段…...

【物联网】深入解析时序数据库TDengine及其Java应用实践
文章目录 一、什么是时序数据库?二、TDengine简介三、TDengine的Java应用实践(1)环境准备(2)数据插入(3)数据查询 一、什么是时序数据库? 时序数据库(Time-Series Datab…...

2023北华大学程序设计新生赛部分题解
时光如流水般逝去,我已在校园中奋战大二!(≧▽≦) 今天,静静回顾去年的新生赛,心中涌起无尽感慨,仿佛那段青春岁月如烟花般绚烂。✧。(≧▽≦)。✧ 青春就像一场燃烧的盛宴,激情澎湃&…...

PPP的配置
概述:PPP模式,即公私合作模式(Public-Private Partnership),是一种公共部门与私营部门合作的模式。 一、实验拓扑 实验一:PPP基本功能 实验步骤: (1)配置AR1的接口IP地…...

回溯算法总结篇
组合问题:N个数里面按一定规则找出k个数的集合 如果题目要求的是组合的具体信息,则只能使用回溯算法,如果题目只是要求组合的某些最值,个数等信息,则使用动态规划(比如求组合中元素最少的组合,…...

机器学习-点击率预估-论文速读-20240916
1. [经典文章] 特征交叉: Factorization Machines, ICDM, 2010 分解机(Factorization Machines) 摘要 本文介绍了一种新的模型类——分解机(FM),它结合了支持向量机(SVM)和分解模型的优点。与…...

【leetcode】堆习题
215.数组中的第K个最大元素 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输…...
和嵌入(Embedding)解析 - llm的输入)
前端大模型入门:编码(Tokenizer)和嵌入(Embedding)解析 - llm的输入
LLM的核心是通过对语言进行建模来生成自然语言输出或理解输入,两个重要的概念在其中发挥关键作用:Tokenizer 和 Embedding。本篇文章将对这两个概念进行入门级介绍,并提供了针对前端的js示例代码,帮助读者理解它们的基本原理/作用和如何使用。 1. 什么是…...

一文读懂 JS 中的 Map 结构
你好,我是沐爸,欢迎点赞、收藏、评论和关注。 上次聊了 Set 数据结构,今天我们聊下 Map,看看它与 Set、与普通对象有什么区别?下面直接进入正题。 一、Set 和 Map 有什么区别? Set 是一个集合࿰…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
