【两方演化博弈代码复现】:双方演化博弈的原理、概率博弈仿真、相位图、单个参数灵敏度演化
目录-基于MatLab2016b实现
- 一、演化博弈的原理
- 1. 基本概念
- 2. 参与者的策略
- 3.演化过程
- 二、MATLAB 代码解读(博弈参与主体(双方)策略选择的动态演化讨程)
- 三、MATLAB 代码解读(博弈主体随着时间策略选择的动态演化讨程)
- 四、两方相位图MATLAB 代码复现
- 五、单一参数灵敏度演化图
- 五、结论
演化博弈论是研究个体在特定环境中如何通过策略选择与其他个体进行互动的学科。这一理论在生物学、经济学和社会科学等多个领域都有广泛应用。本文将深入探讨双方演化博弈的原理及其过程,并解读一段 MATLAB 代码,展示如何模拟这一过程。
一、演化博弈的原理
1. 基本概念
在演化博弈中,参与者(个体)根据其策略与其他参与者进行互动。每种策略在特定环境下的收益决定了这种策略的成功与否。参与者的策略会随着环境的变化而演变,形成“适者生存”的动态过程。
2. 参与者的策略
在一场博弈中,参与者可以选择不同的策略,这些策略的选择影响其在博弈中的收益。例如,在两个玩家的博弈中,常见的策略包括合作与背叛。通过不断的互动与反馈,成功的策略会在种群中逐渐传播。
3.演化过程
演化过程通常可分为以下几个步骤:
初始化:设定参与者的初始状态(策略)。
动态演化:根据参与者策略的收益变化,更新策略选择。
模拟和可视化:使用数学模型和计算机程序模拟演化过程,并通过图形化方式展示结果。
二、MATLAB 代码解读(博弈参与主体(双方)策略选择的动态演化讨程)
以下是用于模拟双方演化博弈的 MATLAB 代码示例:
下面这样的图就是x,y分别为不同参与主体的博弈行为策略概率

下面为复制动态方程函数,需要改成自己的复制动态方程。
注意下面这个代码要单独为一个文件,然后文件的名字,必须和函数的名字一样,比如下面的函数叫dxdt,那么文件名也必须要这个名字
x(1)表示主体1的概率,x(2)表示为主体2的概率,只能这样顺序的表示
所有的演化代码,都需要以这个文件为基础。
function dxdt = taihu(t, x, s, m, c1, c2, r)dxdt = zeros(2, 1); % 初始化一个二元一次的输出dxdt(1) = x(1) * (1 - x(1)) * (r - m - r * x(2)); % x(1) 的变化率dxdt(2) = x(2) * (1 - x(2)) * (s - c1 + c2 - c2 * x(1)); % x(2) 的变化率
end
在设置出来动态方程文件后,再创建一个演化文件,为main文件,这个文件命名没有要求
但是[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]);中taihu表示的是之前设置的复制动态方程的文件,需要和文件名称一致。
clc; clear;s = 10; m = 5; c1 = 20; c2 = 5; r = 10; % 根据实际情况赋值figure(1) % 创建图形窗口% 不同初始条件的演化
[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]);
plot(x(:, 1), x(:, 2), 'rh-'); % 绘制初始值[0.2, 0.8]的演化路径
hold on[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.4, 0.6]);
plot(x(:, 1), x(:, 2), 'mx-'); % 绘制初始值[0.4, 0.6]的演化路径
hold on[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.6, 0.4]);
plot(x(:, 1), x(:, 2), 'bo-'); % 绘制初始值[0.6, 0.4]的演化路径
hold on[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.8, 0.2]);
plot(x(:, 1), x(:, 2), 'gs-'); % 绘制初始值[0.8, 0.2]的演化路径
hold onset(gca, 'XTick', [0:0.1:1], 'YTick', [0:0.1:1]); % 设置坐标轴刻度
axis([0 1 0 1]); % 设置坐标轴范围
xlabel('$x$', 'interpreter', 'latex'); % x 轴标签
ylabel('$y$', 'interpreter', 'latex', 'rotation', 360); % y 轴标签
title('动态演化过程'); % 图形标题
legend('初始值[0.2,0.8]', '初始值[0.4,0.6]', '初始值[0.6,0.4]', '初始值[0.8,0.2]'); % 图例

代码过程分析
函数定义:
taihu 函数定义了两种策略(x(1) 和 x(2))的动态变化率。此函数输入时间 t 和状态 x,以及相关参数 s、m、c1、c2 和 r,并返回 dxdt。
参数设置:
根据实际情况设置参数 s、m、c1、c2 和 r。
使用 ode45 求解:
ode45 是 MATLAB 用于求解常微分方程的函数。在此代码中,使用不同的初始条件 [0.2, 0.8]、[0.4, 0.6]、[0.6, 0.4] 和 [0.8, 0.2] 来模拟演化过程。
绘制演化路径:
使用 plot 函数将每个初始条件下的演化路径绘制在同一图中,便于比较不同策略的动态变化。
图形设置:
设置坐标轴的刻度、范围、标签和标题,并添加图例,以便于理解和分析。
三、MATLAB 代码解读(博弈主体随着时间策略选择的动态演化讨程)
横轴为时间,演化的时间
纵轴为策略的选择概率

以下是代码进行复现的完整 MATLAB 代码:
clc; clear; % 清除命令窗口和工作区变量
s = 10; m = 5; c1 = 20; c2 = 5; r = 10; % 根据实际情况赋值
figure(1) % 创建图形窗口%%%%%%%%%% line1
[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]); % 求解微分方程
plot(t, x(:, 1), '*'); % 绘制与 x1 相关的图形
hold on; % 保持当前图形%%%%%%%%%% line2
[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.4, 0.6]); % 求解微分方程
plot(t, x(:, 2), '*'); % 绘制与 x2 相关的图形
hold on; % 保持当前图形set(gca, 'XTick', 1:1:10, 'YTick', [0:0.1:1]); % 设置坐标轴刻度
axis([0 10 0 1]); % 设置坐标轴范围
xlabel('时间', 'interpreter', 'latex'); % x 轴标签
ylabel('策略值', 'interpreter', 'latex', 'rotation', 360); % y 轴标签
title('动态演化过程'); % 图形标题
legend('策略 x_1', '策略 x_2'); % 图例
其中两个演化图形的关键区别在于:

代码解析
s = 10; m = 5; c1 = 20; c2 = 5; r = 10; % 根据实际情况赋值
这些变量代表模型中的参数,具体含义取决于所研究的博弈模型。
创建图形窗口:
figure(1) % 创建图形窗口
求解微分方程:
[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]); % 求解微分方程
使用 ode45 函数求解常微分方程,taihu 函数定义了模型的动态。
初始条件为 [0.2, 0.8]。
绘制与 x1 相关的图形:
plot(t, x(:, 1), ‘*’); % 绘制与 x1 相关的图形
hold on; % 保持当前图形
再次求解微分方程:
[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.4, 0.6]); % 求解微分方程
plot(t, x(:, 2), ‘*’); % 绘制与 x2 相关的图形
hold on; % 保持当前图形
设置坐标轴:
set(gca, ‘XTick’, 1:1:10, ‘YTick’, [0:0.1:1]); % 设置坐标轴刻度
axis([0 10 0 1]); % 设置坐标轴范围
gca 是获取当前坐标轴的句柄,XTick 和 YTick 设置坐标轴的刻度。
添加标签和标题:
xlabel(‘时间’, ‘interpreter’, ‘latex’); % x 轴标签
ylabel(‘策略值’, ‘interpreter’, ‘latex’, ‘rotation’, 360); % y 轴标签
title(‘动态演化过程’); % 图形标题
legend(‘策略 x_1’, ‘策略 x_2’); % 图例
结果如下所示:

四、两方相位图MATLAB 代码复现
clc; clear; % 清除命令窗口和工作空间
s = 10; m = 5; c1 = 20; c2 = 5; r = 10; % 初始化参数% 外层循环
for i = 0:0.1:1% 内层循环for j = 0:0.1:1[T, Y] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0 100], [i j]); % 求解微分方程figure(1); % 创建或激活图形窗口grid on; % 打开网格plot(Y(:, 1), Y(:, 2)); % 绘制 Y 的第一列和第二列hold on; % 保持当前图形end
end% 设置坐标轴刻度
set(gca, 'XTick', [0:0.1:1], 'YTick', [0:0.1:1]);
xlabel('X'); % x 轴标签
ylabel('Y'); % y 轴标签
代码说明
初始化:
clc; clear; 清除命令窗口和工作空间。
定义一些参数 s, m, c1, c2, r。
双重循环:
外层循环遍历 i 从 0 到 1,以 0.1 为步长。
内层循环遍历 j 从 0 到 1,以 0.1 为步长。
ODE 求解:
使用 ode45 函数求解微分方程,调用自定义的 taihu 函数,时间范围为 [0 100],初始条件为 [i j]。
绘图:
在每次迭代中,创建或激活图形窗口,并绘制 Y 的第一列与第二列的关系。
hold on; 确保所有绘图在同一图形上显示。
设置坐标轴:
使用 set(gca, ‘XTick’, …) 和 ylabel, xlabel 函数设置坐标轴刻度和标签。
注意事项
确保 taihu 函数已定义,并且其输入参数与代码中的一致。
运行此代码需要 MATLAB 环境

发现有空白原点还不是从0开始,修改以下代码:
clc; clear; % 清除命令窗口和工作空间
s = 10; m = 5; c1 = 20; c2 = 5; r = 10; % 初始化参数% 外层循环
for i = 0:0.1:1% 内层循环for j = 0:0.1:1[T, Y] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0 100], [i j]); % 求解微分方程figure(1); % 创建或激活图形窗口grid on; % 打开网格plot(Y(:, 1), Y(:, 2)); % 绘制 Y 的第一列和第二列hold on; % 保持当前图形end
end% 设置坐标轴刻度
set(gca, 'XTick', 0:0.1:1, 'YTick', 0:0.1:1);
xlabel('X'); % x 轴标签
ylabel('Y'); % y 轴标签% 设置坐标轴范围,确保原点重合
axis([0 1 0 1]); % 设置坐标轴范围
set(gca, 'Box', 'on'); % 开启坐标轴框

嗯嗯,这样就可以了
五、单一参数灵敏度演化图
先设置出来,不改变的参数(s;m;c1;c2),
然后单独设置改变的参数(r);
用for循环进入函数;
%% 改变单一参数演化过程图% 主脚本
clc; clear; % 清除命令窗口和工作空间
s = 10; m = 5; c1 = 20; c2 = 5; % 初始化参数figure(1); % 创建图形窗口%%%%%% line1
for r = 10 % 循环参数 r[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]); % 初始条件应为两个元素plot(t, x(:, 1), '*'); % 绘制 t 与 x1 的图像hold on; % 保持当前图形
end%%%%%% line2
for r = 20 % 循环参数 r[t, x] = ode45(@(t, x) taihu(t, x, s, m, c1, c2, r), [0, 10], [0.2, 0.8]); % 初始条件应为两个元素plot(t, x(:, 2), 'o'); % 绘制 t 与 x2 的图像hold on; % 保持当前图形
end% 设置坐标轴刻度
% 设置坐标轴刻度
set(gca, 'XTick', 0:1:10, 'YTick', 0:0.1:1); % 设置 X 和 Y 轴的刻度
axis([0 10 0 1]); % 设置坐标轴范围% 设置 X 轴标签
xlabel('时间', 'Interpreter', 'latex', 'FontWeight', 'bold', 'Fontname', '宋体');
% 设置 Y 轴标签
ylabel('状态变量', 'Interpreter', 'latex', 'Rotation', 360, 'FontWeight', 'bold', 'Fontname', '宋体');
% 设置图形标题
title('动态演化过程', 'Fontweight', 'bold', 'Fontname', '宋体');
% 设置图例
legend('r=10', 'r=20');

这里好像有点问题,和上面的图差不多,代码逻辑应该的没错的,后期还需要再看看,
五、结论
演化博弈论为我们提供了一种分析个体策略选择与环境互动的方法。通过 MATLAB 的编程实现,我们可以模拟并可视化这一复杂的动态过程。希望本文能够帮助您理解双方演化博弈的基本原理与实现方法,欢迎您在实践中进一步探索和应用这一理论!
相关文章:

【两方演化博弈代码复现】:双方演化博弈的原理、概率博弈仿真、相位图、单个参数灵敏度演化
目录-基于MatLab2016b实现 一、演化博弈的原理1. 基本概念2. 参与者的策略3.演化过程 二、MATLAB 代码解读(博弈参与主体(双方)策略选择的动态演化讨程)三、MATLAB 代码解读(博弈主体随着时间策略选择的动态演化讨程&a…...

Selenium打开浏览器后闪退问题解决
笔者这两天在做一个自动化方案,用来优化数据统计。其中一部分数据需要通过云上堡垒机跳转访问,而这个堡垒机在笔者日常使用的火狐浏览器上运行不是很正常(表现在有些复制粘贴按钮显示不太灵敏)。 但在Edge浏览器上基本正常&#…...

【图论】最短路应用
1135. 新年好 题目 提交记录 讨论 题解 视频讲解 MarkDown视图Copy 重庆城里有 nn 个车站,mm 条 双向 公路连接其中的某些车站。 每两个车站最多用一条公路连接,从任何一个车站出发都可以经过一条或者多条公路到达其他车站,但不同的…...

Spring Boot实战:使用策略模式优化商品推荐系统
在现代电子商务平台中,个性化的商品推荐系统是提升用户体验和增加销售额的关键。本文将通过一个Spring Boot实战项目,展示如何利用Java的设计模式——策略模式,来优化商品推荐系统。同时,我们将探讨Spring Boot中的一个重要特性&a…...

Navicat导入Sql文件至Mysql数据库,事务失效
Mysql 版本:8.0.39 Navicat 版本:17.x、16.x 结论: Navicat 导入sql文件,事务不会生效,无论怎么设置 mysql.exe 导入sql文件,事务生效 测试 准备一张表 name约束不能为空,用于测试事务失败…...

篮球运动场景物体检测系统源码分享
篮球运动场景物体检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Comp…...
Docker实操:安装MySQL5.7详解(保姆级教程)
介绍 Docker 中文网址: https://www.dockerdocs.cn Docker Hub官方网址:https://hub.docker.com Docker Hub中MySQL介绍:https://hub.docker.com/_/mysql 切换到“Tags”页面,复制指定的MySQL版本拉取命令,例如 :…...

git reflog
git reflog 是一个非常有用的命令,可以让你查看和回滚到 Git 仓库中的任何之前的状态。reflog 记录了你在 Git 仓库中的所有 HEAD 移动历史。下面是使用 reflog 回滚到之前状态的步骤: 1. 查看 Reflog 首先,你需要查看 reflog 记录…...

使用 Vue 3 和 TypeScript 实现带打字效果的仿 AI 分析展示组件
在这篇博客中,我将分享如何用 Vue 3 和 TypeScript 实现一个带打字效果的 AI 分析展示组件。该组件具有如下功能: 动态打字效果:模拟打字机逐步显示内容。自动滚动:内容超出容器高度时自动滚动到最新位置。 1. 组件实现需求 我…...

数据清洗-缺失值填充-K-NN算法(K-Nearest Neighbors, K-NN算法)
目录 一、安装所需的python包二、采用K-NN算法进行缺失值填充2.1代码(完整代码关注底部微信公众号获取)2.2以某个缺失值数据进行实战2.2.1代码运行过程截屏:2.2.2填充后的数据截屏: 三、K 近邻算法 (K-Nearest Neighbors, KNN) 介…...

爬虫----webpack
目录 一. 什么是webpack 出现的原因:同名函数 概念: 特征:大量缩进 webpack的格式 简单的webpack格式: 详细的webpack格式: 几个参数的运用 1. webpack数组形式 2. webpack对象格式 3.多个js文件打包 打印要扣的代码 …...

Spring Mybatis PageHelper分页插件 总结
1.简介 使用分页插件可以帮助我们自动分页,不用手动在写sql的分页逻辑。 2.配置步骤 在pom.xml中添加依赖 <dependency><groupId>com.github.pagehelper</groupId><artifactId>pagehelper</artifactId><version>5.1.11<…...

9、等保测评介绍
数据来源:9.等保测评介绍_哔哩哔哩_bilibili 信息系统等级测评 信息系统等级测评是测评机构依据国家信息安全等级保护制度的规定,按照相关管理规范和技术标准,对未涉及国家秘密的信息系统的安全等级保护状况进行检测评估的活动。 等级测评…...

解决Gson将长数字( json字符串)转换为科学记数法格式
Gson(又称Google Gson)是Google公司发布的一个开放源代码的Java库,主要用途为序列化Java对象为JSON字符串,或反序列化JSON字符串成Java对象。 依赖 Gradle: dependencies {implementation com.google.code.gson:gson:2.11.0 }…...

php环境搭建教程
PHP环境搭建教程 在构建和开发PHP应用程序时,搭建一个稳定、高效的PHP环境是基础且关键的一步。本教程将详细介绍如何在不同操作系统(Windows和Linux)上搭建PHP环境,包括Apache服务器的安装与配置、PHP的安装与配置、MySQL的安装…...

测试ASP.NET Core的WebApi项目调用WebService
虚拟机中部署的匿名访问的WebService,支持简单的加减乘除操作。本文记录在WebApi中调用该WebService的方式。 VS2022创建WebApi项目,然后在解决方案资源管理器的Connected Services节点点右键,选择管理连接的服务菜单。 点击下图圈红处…...

【用Java学习数据结构系列】对象的比较(Priority Queue实现的前提)
看到这句话的时候证明:此刻你我都在努力 加油陌生人 个人主页:Gu Gu Study 专栏:用Java学习数据结构系列 喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹 喜欢的话可以点个赞谢谢了。 作者ÿ…...
)
快手视频怎么保存到相册?(详细操作)
随着短视频的流行,快手已经成为越来越多人日常生活的一部分。无论是搞笑片段、旅行记录,还是生活点滴,用户们每天都会在快手上浏览到大量有趣的视频。有时候,我们会遇到特别想保存的视频,想要分享到朋友圈,…...

为什么 ECB 模式不安全
我们先来简单了解下 ECB 模式是如何工作的 ECB 模式不涉及链接模式,所以也就用不着初始化向量,那么相同的明文分组就会被加密成相同的密文分组,而且每个分组运算都是独立的,这也就意味着可以并行提高运算效率,但也正是…...
『功能项目』事件中心处理怪物死亡【55】
本章项目成果展示 我们打开上一篇54回调函数处理死亡的项目, 本章要做的事情是用事件中心处理怪物死亡后的逻辑 首先打开之前事件中心脚本(不做更改,调用即可): using System.Collections.Generic; using UnityEngine…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
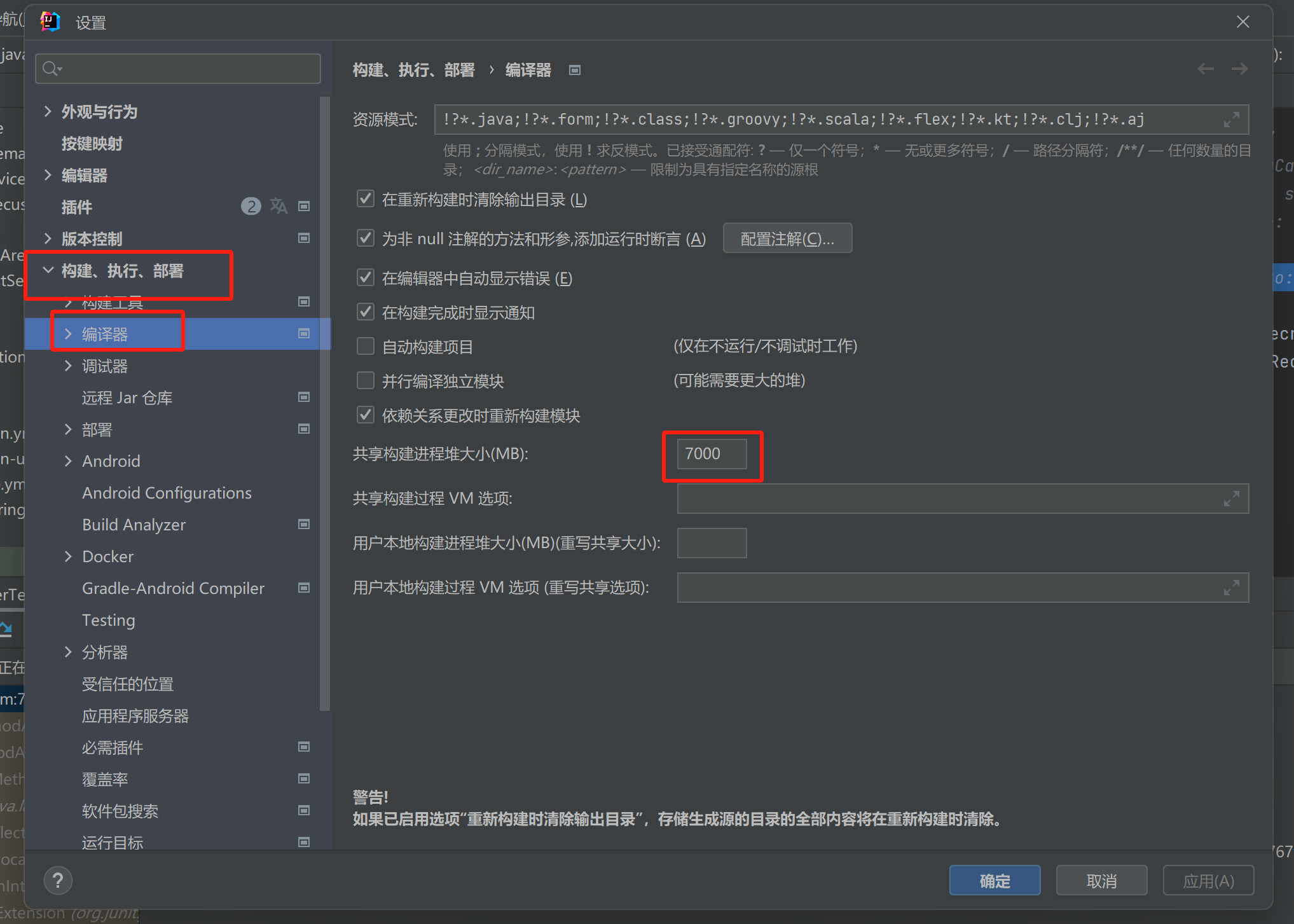
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
