希尔排序(C语言实现)
目录
1.希尔排序( 缩小增量排序 )
2.动图 编辑
3.代码实现
预排序实现
子序列排列实现
单趟排序实现
对整组数进行子排序
希尔排序代码
代码测试
时间复杂度分析
希尔排序的特性总结:

1.希尔排序( 缩小增量排序 )
基本思想:
1.先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并 对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重 复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
2.动图 
3.代码实现
思路:
预排序实现
插入排序
预排序实现
根据当前增量,数组被分为若干子序列,这些子序列的元素在原数组中间隔着固定的增量。对每个子序列应用插入排序。
假设最初增量为5

d越大,数据挪动得越快;d越小,数据挪动得越慢。前期让d较大,可以让数据更快得移动到自己对应的位置附近,减少挪动次数。
注:一般情况下,取序列的一半作为增量,然后依次减半,直到增量为1(也可自己设置)。
完成了一轮希尔排序,此时整个数组并不完全有序,但是已经比原始的数组更接近有序了。然后减小增量,通常是将原来的增量除以2(或者除以3+1),现在选择下一个增量为 2,按照此排序规则继续预排序即可,直到增量为1时,则为直接插入排序,此时则排序完成。
子序列排列实现
//子序列int gap;int end;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + 3] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;这里只需要在插入排序的基础上修改一下即可。end的所加所减都为gap;
单趟排序实现
int gap;//单趟排序实现for (int i = 0; i < n - gap; i += gap){//子序列int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + 3] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}这里的 n-gap 和插入排序中的 n-1 一样是为了防止越界
对整组数进行子排序
int gap;for (int j = 0; j < gap; j++){//单趟排序实现for (int i = 0; i < n - gap; i += gap){//子序列int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + 3] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}外层循环
(for (int j = 0; j < gap; j++))意在对每个以gap为间隔的分组进行遍历。
这里进行一下优化:
三层代码的循环是每一组子排序排完再进行下一组,直到排完整个数组。
下面这组代码优化后效率并没有很大的提升,只是代码更为简洁。
这组代码是齐头并进,排完第一组的前n个就排下一组了,并没有把第一组全部排完。
int gap;for (int i = 0; i < n - gap; i++){//子序列int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + 3] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
希尔排序代码
分析
gap越大,大的值更快调到后面,小的值更快调到前面,越不接近有序。
gap越小,大的值更慢调到后面,小的值更慢调到前面,越接近有序。
当gap为1,就是直接插入排序。
所以我们这里的gap值应该是在变化的,一般我们随n变化,取gap = gap/3+1,或者gap = gap/2;
void ShellSort(int* a,int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){//子序列int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}这里无论gap是奇数还是偶数,这里gap最终都会除以到值为1。
gap>1时是预排序,目的让其接近有序。
gap=1时是直接插入排序,目的让其有序。
在gap=1时,已经十分接近有序了
代码测试

时间复杂度分析
希尔排序的时间复杂度并不固定,它依赖于所选择的间隔序列(增量序列)。直到今天,已经有多种不同的间隔序列被提出来,每种都有自己的性能特点。
《数据结构(C语言版)》--- 严蔚敏

《数据结构-用面相对象方法与C++描述》--- 殷人昆
 因为咋们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:O(N^1.25) 到 O(1.6* N^1.25) 来算。
因为咋们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:O(N^1.25) 到 O(1.6* N^1.25) 来算。
希尔排序的特性总结:
时间复杂度:O(N²)
空间复杂度:O(1)
稳定性:不稳定
复杂性:简单
如有错误,请指正
相关文章:

希尔排序(C语言实现)
目录 1.希尔排序( 缩小增量排序 ) 2.动图 编辑 3.代码实现 预排序实现 子序列排列实现 单趟排序实现 对整组数进行子排序 希尔排序代码 代码测试 时间复杂度分析 希尔排序的特性总结: 1.希尔排序( 缩小增量排序 ) 基本思想: 1.先选定一个…...

LLVM 中的Value、User、Use设计
概述 LLVM是一个强大的编译器基础设施,提供了一套丰富的库,用于构建编译器的前端和后端。在LLVM中,Value、User和Use是几个核心的概念,它们之间有着紧密的关系 Value Value是LLVM中表示所有可计算的值的基类,例如常…...
)
C++智能指针入门教程(C++11)
智能指针 1.定义 C中的智能指针是一种用于自动管理动态分配的内存的模板类,它们通过封装原始指针来提供自动的内存管理功能,从而避免了内存泄漏和悬挂指针等问题。C标准库中提供了几种智能指针类型,其中最常用的是std::unique_ptr、std:…...

常用工具推荐!分享7款AI论文修改软件工具网站
在当今学术研究和写作领域,AI论文修改软件工具已经成为了不可或缺的助手。这些工具不仅能够帮助研究人员提高写作效率,还能确保论文的质量和原创性。以下是七款值得推荐的AI论文修改软件工具网站,其中特别推荐千笔-AIPassPaper。 1. 千笔-AI…...

怎么解除BitLocker对磁盘的加密?
BitLocker是一种Windows操作系统内置的加密功能,用于保护用户的数据安全。它通过对整个磁盘进行加密,防止数据被未经授权的用户访问。BitLocker主要用于保护笔记本电脑和台式机中的重要数据,尤其是在设备丢失或被盗的情况下。怎么解除BitLock…...
群晖使用Docker部署WPS Office并实现异地使用浏览器制作办公文档
文章目录 前言1. 本地环境配置2. 制作本地分享链接3. 制作公网访问链接4. 公网ip地址访问您的分享相册5. 制作固定公网访问链接 前言 想象一下这个场景:如果遇到周末紧急需要改方案,但团队成员都在各自家中,这个时候如果大家能够轻松访问这个…...

Unity3d 以鼠标位置点为中心缩放视角(正交模式下)
思路整理: 缩放前: 缩放后: 记录缩放前鼠标的屏幕坐标 A,计算鼠标位置对应的世界坐标 A_world 缩放完成后,根据当前屏幕下A所对应的世界坐标A1_world 计算A1_world 和 A_world 的偏移量 移动摄像机 代码ÿ…...

Git清除某文件所有历史提交记录
一、软件要求 1.1 软件版本要求 git > 2.22.0python3 > 3.5 1.2 辅助插件 git filter-repo Linux/macOS # Debian/Ubuntu 系统 # 或使用 pip 安装pip install git-filter-repo sudo apt install git-filter-repo Windows pip install git-filter-repo二、操作步骤…...
jacoco生成单元测试覆盖率报告
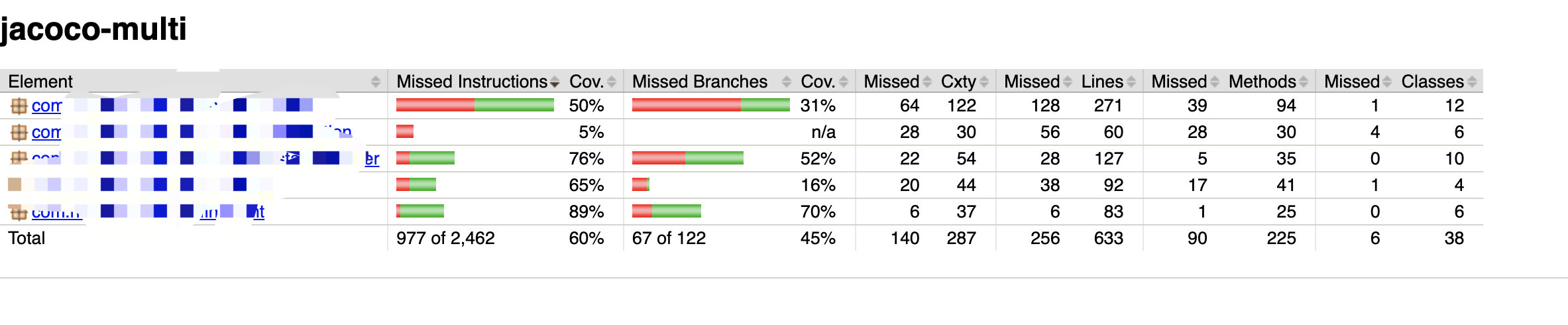
前言 单元测试是日常编写代码中常用的,用于测试业务逻辑的一种方式,单元测试的覆盖率可以用来衡量我们的业务代码经过测试覆盖的比例。 目前市场上开源的单元测试覆盖率的java插件,主要有Emma,Cobertura,Jacoco。具体…...

【CSS Tricks】如何做一个粒子效果的logo
效果展示 代码展示 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>粒子效果Logo</title>…...

如何使用ssm实现基于Javaweb的网上花店系统的设计与实现
TOC ssm653基于Javaweb的网上花店系统的设计与实现jsp 研究背景 自计算机发展以来给人们的生活带来了改变。第一代计算机为1946年美国设计,最开始用于复杂的科学计算,占地面积、开机时间要求都非常高,经过数十几的改变计算机技术才发展到今…...

Elastic 的 OpenTelemetry PHP 发行版简介
作者:Pawel Filipczak 宣布 OpenTelemetry PHP 的 Elastic 发行版的第一个 alpha 版本。在本篇博文中了解使用 OpenTelemetry 来检测 PHP 应用程序是多么简单。 我们很高兴推出 OpenTelemetry PHP 的 Elastic Distribution 的第一个 alpha 版本。在这篇文章中&…...

TCP 和 UDP 协议的区别?
参考TCP 和 UDP的区别_tcp和udp的区别-CSDN博客...

【PHP】使用thinkphp5查询最大值时,把varchar类型字段转换成数字
有时候我们需要把carchar类型的字段进行聚合函数运运行(max、min、avg),但是如果直接用聚合函数,得到的结果是错误的,因为varchar字段是字符串,无法直接使用聚合函数,所以需要把varchar字段转换…...

Java 正则表达式详解
正则表达式 (Regular Expression,简称 regex) 是一种强大的文本处理工具,可以用来匹配、搜索和替换文本中的特定模式。在 Java 中,正则表达式由 java.util.regex 包提供支持。 1. 理解正则表达式语法 正则表达式使用特殊的字符和符号来定义…...
MySQL篇(窗口函数/公用表达式(CTE))(持续更新迭代)
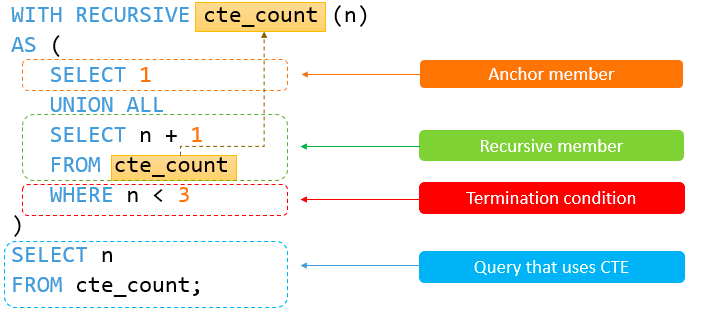
目录 讲解一:窗口函数 一、简介 二、常见操作 1. sumgroup by常规的聚合函数操作 2. sum窗口函数的聚合操作 三、基本语法 1. Function(arg1,..., argn) 1.1. 聚合函数 sum函数:求和 min函数 :最小值 1.2. 排序函数 1.3. 跨行函数…...

Jira Cloud涨价5%-20%,钉钉项目Teambition成优选替代
近日,Jira再次宣布涨价,Cloud版涨幅达到5%-20%,这一消息来源于Atlassian官方面向合作伙伴发布的2024年最新涨价通知。 Atlassian旗下核心产品,包括Jira、Confluence、JiraServiceManagement等的Cloud版本价格将有所提高ÿ…...

Python语言基础教程(下)4.0
✨博客主页: https://blog.csdn.net/m0_63815035?typeblog 💗《博客内容》:.NET、Java.测试开发、Python、Android、Go、Node、Android前端小程序等相关领域知识 📢博客专栏: https://blog.csdn.net/m0_63815035/cat…...
【HTTP】构造HTTP请求和状态码
状态码 用于响应中,表示响应的结果如何 正确?错误?什么原因? HTTP 中的状态码都是标准约定好的 200 OK 成功了,一切顺利 在抓包到的响应中 404 Not Found 访问的资源(URL 中的路径)没找…...

Delta Lake如何使用
1. 安装 Java 确保你的系统上安装了 Java 8 或更高版本。可以通过以下命令检查 Java 是否已安装: java -version2. 安装 Apache Spark 下载 Spark: 从 Apache Spark 官方网站 下载适合的版本,建议下载预编译的版本(例如…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
