第 100002(十万零二)个素数是多少?
题目描述
素数就是不能再进行等分的整数。比如7,11。而 9 不是素数,因为它可以平分为 3 等份。一般认为最小的素数是2,接着是 3,5,...
请问,第 100002(十万零二)个素数是多少?
请注意:“2” 是第一素数,“3” 是第二个素数,依此类推。
运行限制
最大运行时间:1s
最大运行内存: 128M
题目分析
对于这道题来说,难点在于运行时间只要1秒钟的问题
这个问题核心解决在于对素数的判定能不能够更快一点
先来看第一种,也是最慢的一种

第二种 稍微快一点

他确实也是快了一点点,但是可以帮我们解决问题吗?
确实能解决问题,但是运行的非常慢,时间复杂度是O(n)
第三种,采用sqrt开根号的方式来继续这半找素数
这个方法比上面排查的数据更少
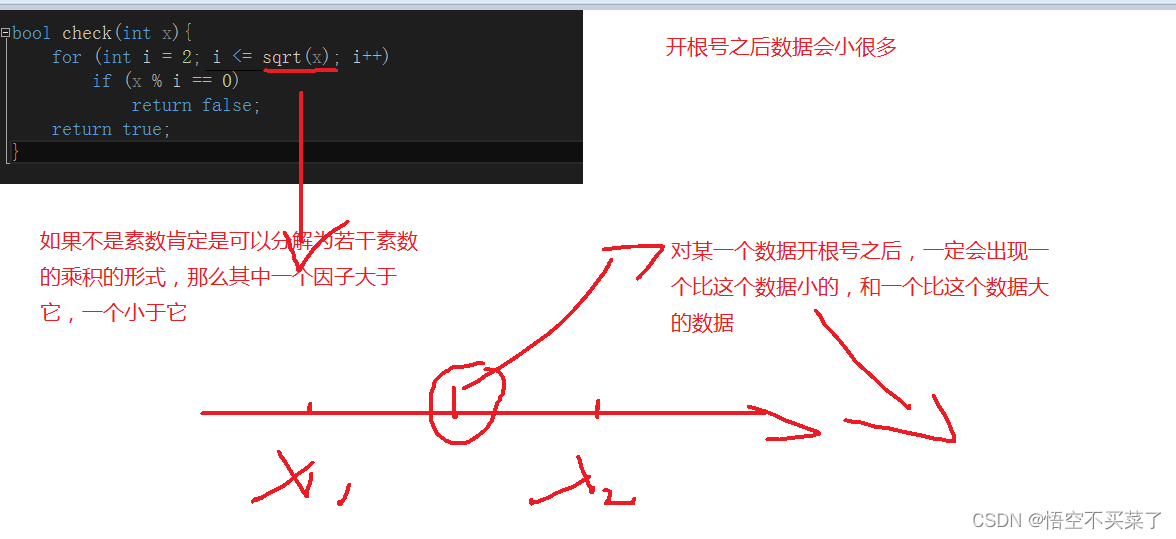
这个时间复杂度应该就是O(sqrt(n))
相对于上面的来说还是要快一点
第四种, 直接卡到x/i这个位置
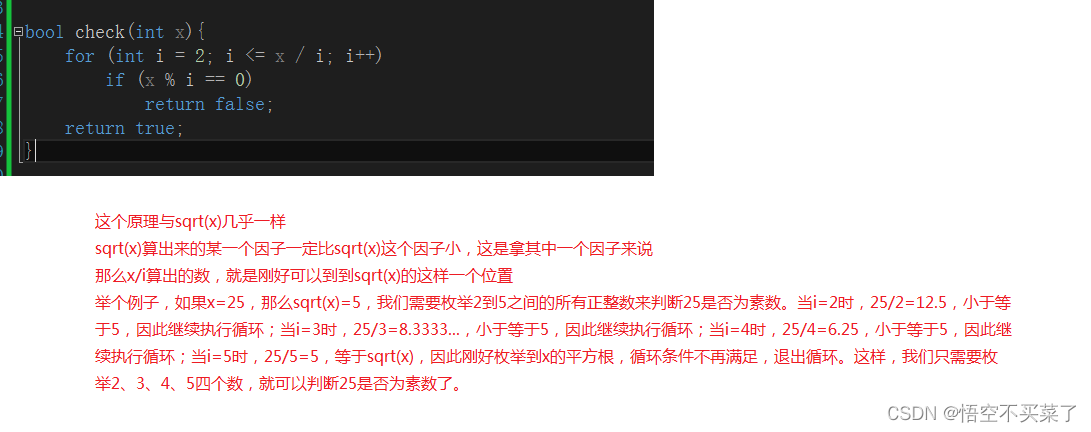
我们还可以列举出更大的质数来进行测试

每一个数都会除一下,基本上也是除到sqrt(x)这样一个位置
上面这道题基本上来说,就解决了。
知识拓展
讲一个查找20以内的所有素数,假定是查找到20,但是这个数据这个可能更大,这里我们用一种埃氏筛选法
来说一下原理

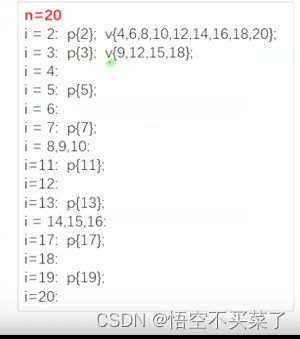
这里贴一下测试代码
#include <stdio.h>
#include <stdlib.h>typedef long long ll;
//定义数组的大小
const int N = 10000000;//一千万个数据int visit[N];//记录合数
int cnt=0;//与prime关联的一个游标
int prime[N];//记录质数//找出到<= N这样一个素数的一个查找
void find_prime(int n)
{//外层循环,循环整体for(int i = 2;i <= n;i++) {//如果等于0的情况,就是一个质数if(!visit[i]) {prime[cnt++] = i;//它的倍数一定是一个合数,然后按步长增长for(ll j = i*i;j<=n;j+=i) {//全是合数visit[j] = 1;//相应的i就是1 }}}
}int main()
{find_prime(20);for(int i = 0;i < cnt;i++) {printf("%d ",prime[i]); }return 0;
}下面在来说另外一种素数筛选方法
欧拉筛选也叫线性筛选法
用两句话来说明一下线性筛选法
第一:每一个合数都是被它的一个最小因子筛选掉的
第二:如果当前被筛选的是一个质数,那么质数*质数是可以筛选掉一部分合数,其实也是通过最小因子算出来的
第三:用已知的素数去筛选合数,避免重复筛选,避免重复筛选这个过程,就是一个位置,如果一旦被标记为合数之后,就不要重复标记为合数
一张图来说明一下线性筛选法

demo2.cpp
#include <stdio.h>
#include <stdlib.h>
#include <vector>using namespace std;vector<int> get_primes(int n)
{vector<int> primes;vector<bool> is_prime(n+1,true);//默认为true的情况下其实是为这质数的//下面开始循环for(int i = 2;i <= n;i++) {if(is_prime[i]) {primes.push_back(i);}for(int j = 0;j < primes.size() && i * primes[j] <= n;j++) {//只要有因子这个数标记为falseis_prime[i * primes[j]] = false;//避免重复标记if(i % primes[j] == 0) {break;}}}return primes;//返回一个vector数组
}int main()
{vector<int> res = get_primes(20);//采用for循环的方式进行打印vector<int>::iterator it_begin = res.begin();vector<int>::iterator it_end = res.end();//采用for循环的方式for(it_begin;it_begin != it_end;it_begin++) {printf("%d ",*it_begin);}printf("\n-------------------\n");//这里说过prime可以看成一个数组for(int i = 0;i < res.size();i++) {printf("%d ",res[i]);//本身就可以当成数组对待}return 0;
}
相关文章:

第 100002(十万零二)个素数是多少?
题目描述 素数就是不能再进行等分的整数。比如7,11。而 9 不是素数,因为它可以平分为 3 等份。一般认为最小的素数是2,接着是 3,5,... 请问,第 100002(十万零二)个素数是多少? 请注意࿱…...

Lua迭代器
Lua迭代器 迭代器(iterator)是一种对象,它能够用来遍历标准模板库容器中的部分或全部元素,每个迭代器对象代表容器中的确定的地址。 在 Lua 中迭代器是一种支持指针类型的结构,它可以遍历集合的每一个元素。 泛型 f…...

同步与互斥之信号量
目录 1、信号量用于线程的互斥 验证 2、信号量用于线程的同步 验证 3、无名信号量用于进程间互斥 代码一 代码二 验证 4、有名信号量 用于进程间同步和互斥 验证 信号量广泛用于进程或线程间的同步和互斥,信号量本质上是一个非负的整数计数器,它…...

如何当个优秀的文档工程师?从 TC China 看技术文档工程师的自我修养
本文系 NebulaGraph Community Academic 技术文档工程师 Abby 的参会观感,讲述了她在中国技术传播大会分享的收获以及感悟。 据说,技术内容领域、传播领域的专家和决策者们会在中国技术传播大会「tcworld China 2022」大会上分享心得。作为一名技术文档工…...

如何学习k8s
学习Kubernetes可以遵循以下步骤: 了解Kubernetes的基本概念和架构。学习Kubernetes前,需要了解它的基本概念和组成部分,包括Pod、Service、ReplicaSet、Deployment、Namespace等等,同时也需要了解Kubernetes的整体架构和工作原理…...
)
【SSM】MyBatis(十.动态sql)
文章目录1.if2.where3.trim4.set5. choose when otherwise6.foreach6.1 批量删除6.2 批量增加7.sql1.if <select id"selectByMultiCondition" resultType"Car">select * from t_car where 1 1<if test"brand ! null and brand ! ">…...
最近很多人都在说 “前端已死”,讲讲我的看法
转自 : 掘金 作者 : Ethan_Zhou 现状 我记得去年脉脉的论调还都是 客户端已死,前后端还都是一片祥和,有秀工资的,有咨询客户端转前端的,怎么最近打开脉脉一看,风向变了? 随便刷几下,出来的信息…...

大家好,我是火旺技术
大家好,我是火旺技术 在Internet高速发展的今天,我们生活的各个领域都涉及到计算机的应用。这其中,家乡特色推荐的网络应用已经成为外国家乡推荐系统的一种很普遍的方式。不过,在国内,管理网站可能还处于起步阶段。 …...
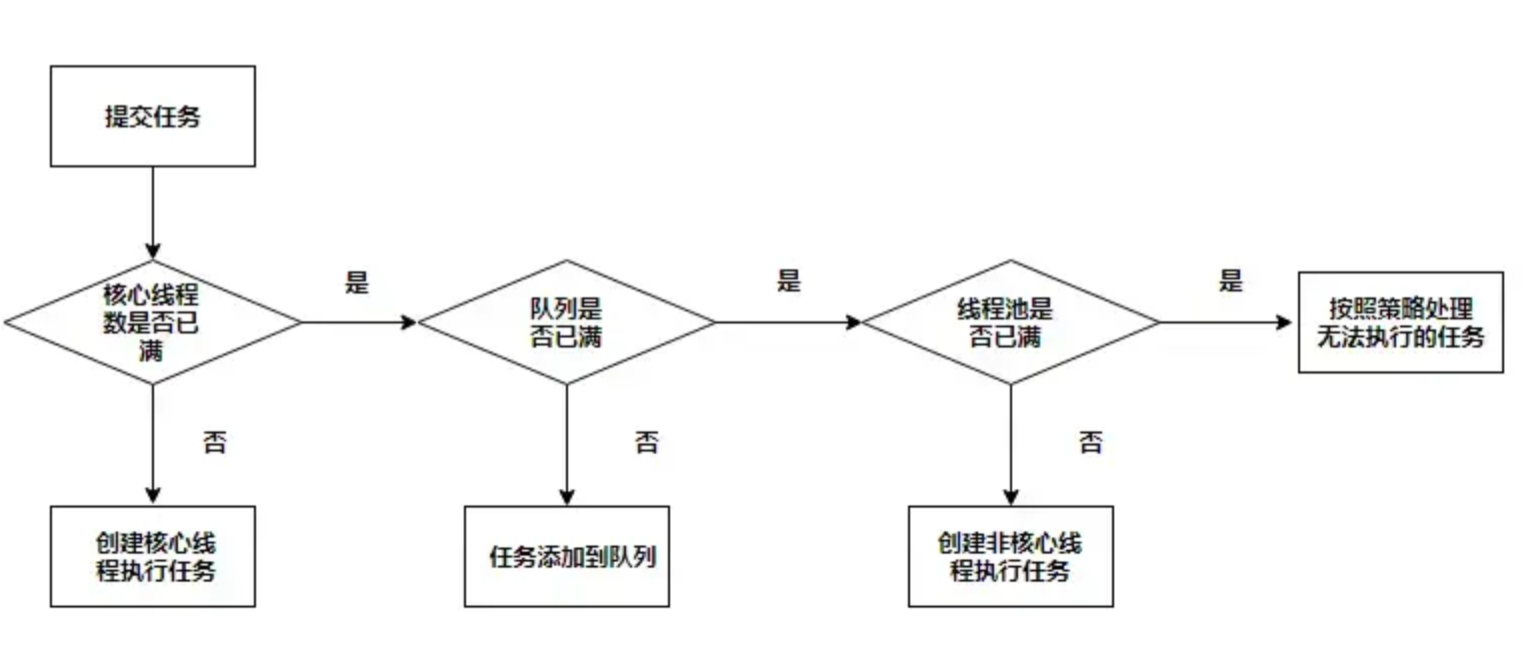
【Java并发编程系列】全方位理解多线程几乎包含线程的所有操作哦
文章目录一、概述及目录二、实现多线程的方式2.1 继承Tread类,重写run方法。start方法2.2 实现Runnable方法,并实现run接口方法2.3 实现Callable接口重写call方法,Feature.get()获取返回值三、线程的执行流程3.1 执行流程3.2 start方法和 run…...

天宝S6测量机器人/天宝S6全站仪参数/教程/Trimble 天宝全站仪
TRIMBLE DR PLUS技术 Trimble DR Plus™距离测量技术实现更大范围的直接反射测量,不使用棱镜也能进行长距离测量。难以抵达或不安全的测 量目标,对Trimble S6来说不再是问题。Trimble DR Plus结合 了MagDrive™磁驱伺服技术,使测量的快捷和…...

c++基础知识汇总
目录 1、基础 1.2 注释 1.3 变量 1.4 常量 1.5 关键字 1.6 标识符命名规则 2 数据类型 2.1 整型 2.2 sizeof关键字 2.3 实型(浮点型) 2.4 字符型 2.5 转义字符 2.6 字符串型 2.7 布尔类型 bool 2.8 数据的输入 1、基础 1.2 注释 作用&a…...
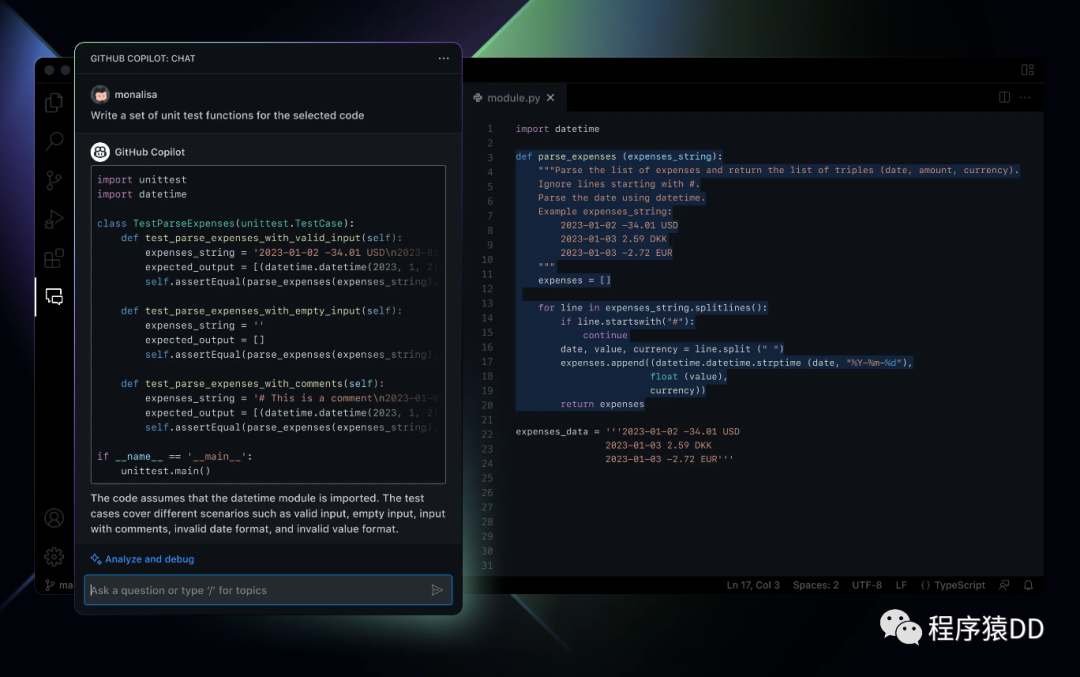
重磅!基于GPT-4的全新智能编程助手 GitHub Copilot X 来了!
GitHub Copilot相信大家一定不陌生了,强大的智能代码补全功能一度让媒体直呼程序员要被替代。随着OpenAI推出全新的GPT-4,GitHub Copilot也在3月22日,推出了全新一代产品:GitHub Copilot X 。最新的GitHub Copilot X 不仅可以自动…...
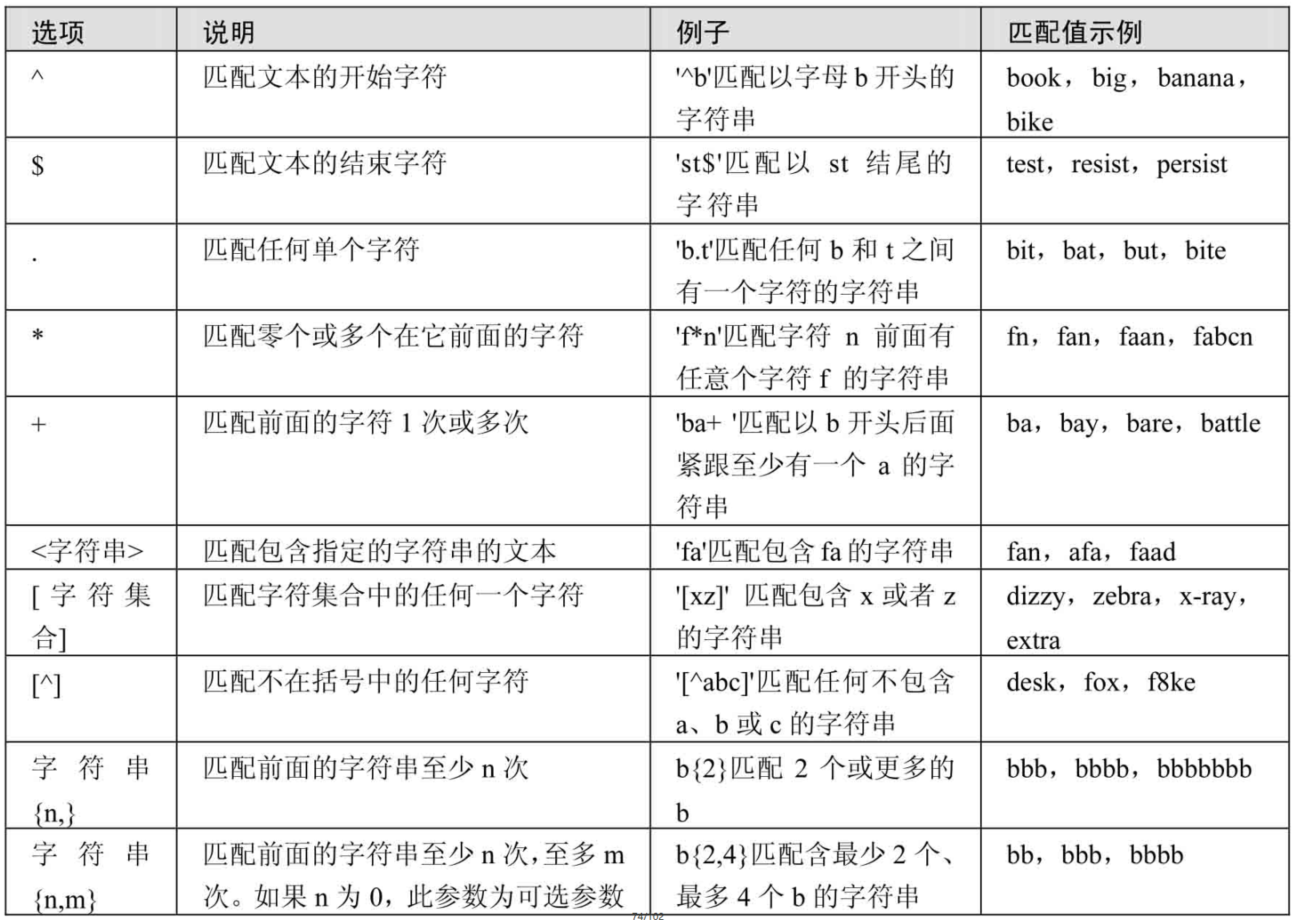
第04章_运算符
第04章_运算符 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公…...

Excel 文件比较工具:xlCompare 11.0 Crack
(Excel 文件比较工具)xlCompare 11.0 下载并安装最新版本的 xlCompare。下载是一个功能齐全的版本。 筛选匹配的行 筛选不同的行 仅显示两个 Excel 文件中存在的行,并排除新(已删除)行 隐藏在另一张工作表上具有相应行…...
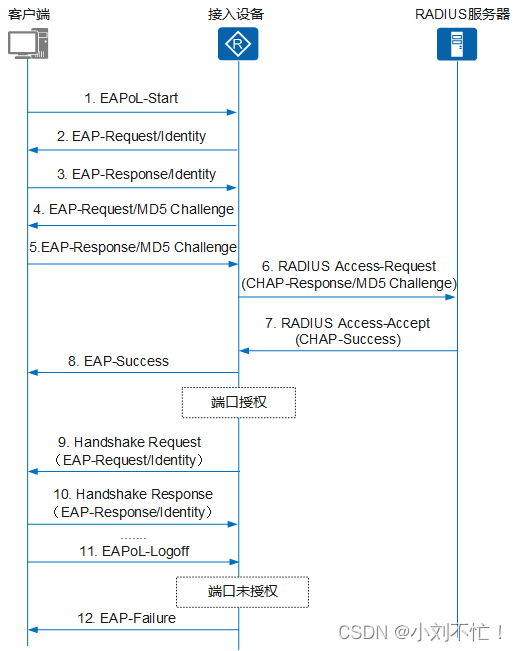
802.1x认证原理
802.1x认证原理802.1X认证简介802.1X认证协议802.1X认证流程802.1X认证简介 定义:802.1x协议是一种基于端口的网络接入控制协议。基于端口的网络接入控制,是指在局域网接入设备的端口这一级验证用户身份,并且控制其访问权限。优点࿱…...
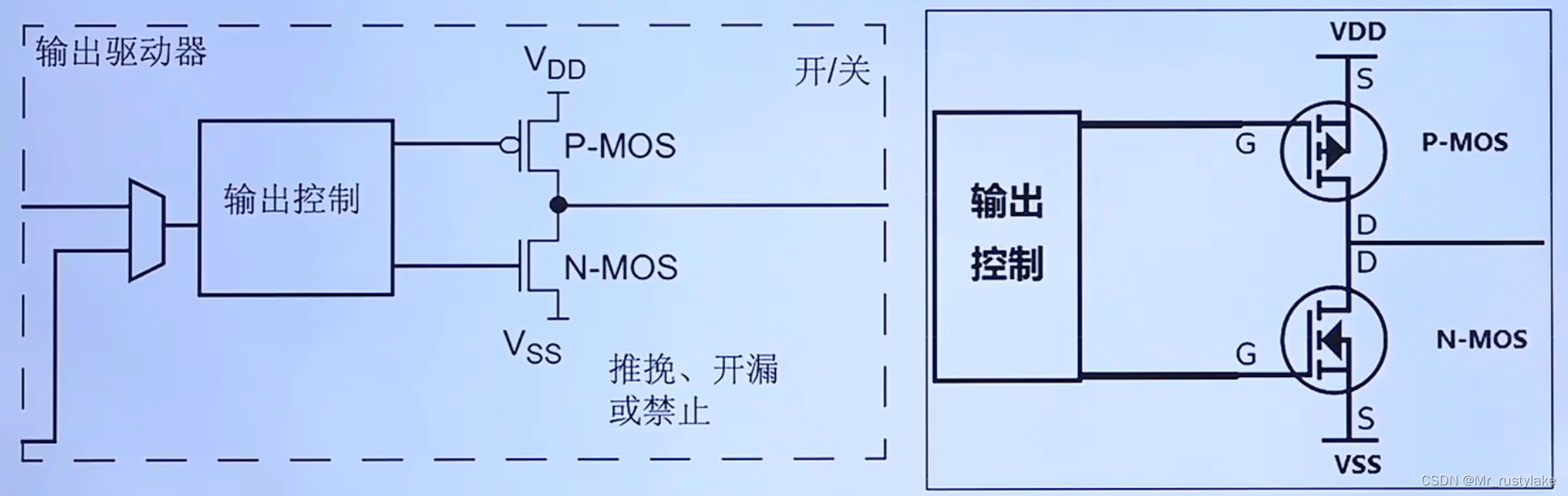
GPIO的八种模式分析
GPIO是general purpose input output,即通用输入输出端口,作用是负责外部器件的信息和控制外部器件工作。 GPIO有如下几个特点:1.不同型号的IO口数量不同;2,反转快速,每次翻转最快只需要两个时钟周期,以ST…...

携职教育:财会人常用必备,203个EXCEL快捷键汇总
会用快捷键的人早下班! 作为财务人员如果你想要提高工作效率,不掌握一些Excel快捷键怎么行? 老板看见了,也会赞一声,“看,这就是专业。” 立马给你加薪(划掉),工作效率这…...

【美赛】2023年ICM问题Z:奥运会的未来(思路、代码)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

CSS基础入门
CSS基础之语法 介绍 CSS(层叠样式表)是一门用来设计网页样式的语言,如网页的布局、字体、颜色搭配、视觉特效。作为WEB开发的基础技术之一,掌握CSS的语法和API对于我们构建丰富的网页是必须的。 基础语法 <style>div …...

可重入锁、读写锁、邮戳锁 详解
文章目录1、可重入锁(递归锁)2、读写锁2.1、读写分离2.2、从写锁到读锁,ReentrantReadWriteLock可以降级2.3、写锁和读锁是互斥的3、邮戳锁StampedLock3.1、是什么3.2、锁饥饿3.3、如何缓解锁饥饿问题呢3.3.1、使用“公平”策略3.3.2、Stampe…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
