逻辑回归 和 支持向量机(SVM)比较
为了更好地理解为什么在二分类问题中使用 SVM,逻辑回归的区别,我们需要深入了解这两种算法的区别、优势、劣势,以及它们适用于不同场景的原因。
逻辑回归和 SVM 的比较
1. 模型的核心思想
• 逻辑回归:
• 基于概率的模型:逻辑回归是一种概率模型,它预测的是样本属于某个类别的 概率值。其假设函数是通过 Sigmoid 函数 将输入映射到 0 到 1 之间的概率。最后通过设定一个阈值(通常为 0.5),来决定样本属于哪个类别。
• 线性决策边界:逻辑回归假设类别可以通过一个线性决策边界分开。例如在二维空间中,逻辑回归找到的是一条直线,在更高维空间中则是一条超平面。
• SVM:
• 基于最大间隔的模型:SVM 并不是像逻辑回归那样输出概率,而是直接找到 分隔不同类别的超平面,并且保证该超平面与最近的样本(支持向量)之间的距离 最大化,从而增强模型的 泛化能力。
• 最大间隔决策边界:SVM 选择的决策边界不仅要正确地分类样本,还要保证分隔两类样本的间隔尽可能大。这样可以让模型在面对新的样本时具有更好的稳定性和鲁棒性。
2. 损失函数与优化目标
逻辑回归:
• 逻辑回归使用的是 对数似然损失(Log-Loss)。其目标是通过最小化这个损失函数,使得模型预测出的概率与真实的类别值之间的误差最小化。
• 优化目标是找到模型参数 w 和 b ,使得预测的概率尽量接近真实的类别。
SVM:
• SVM 使用的是 hinge loss 损失函数,其目标是最大化决策边界与支持向量的间隔。换句话说,SVM 会找到一个使分类正确且 间隔最大 的超平面。
• 优化目标是找到能够最大化分类间隔的决策边界,而不仅仅是将样本正确分类。
3. 如何处理非线性问题
• 逻辑回归:
• 逻辑回归是 线性模型,它的决策边界是线性的。如果数据是非线性的(例如无法通过一条直线或一个超平面分割),逻辑回归在原始特征空间中无法很好地解决问题。
• 为了处理非线性问题,逻辑回归可以通过 特征扩展(如多项式特征)来引入非线性,但这需要手动添加额外的特征。
• SVM:
• SVM 的一个核心优势是使用 核方法(Kernel Trick),它能够自动将数据映射到更高维的空间,在这个新空间中找到一个线性决策边界。因此,SVM 可以在 原始数据不可线性分割的情况下,通过核函数将其转化为线性可分。
• 常用的核函数有 RBF核(高斯核)、多项式核等,它们能够很好地处理复杂的非线性问题。
4. 对噪声数据的敏感性
• 逻辑回归:
• 逻辑回归是一种基于概率的模型,对噪声数据相对不太敏感。即使数据中存在一些不易分类的样本,逻辑回归仍然可以通过概率分布合理地处理。
• SVM:
• SVM 对噪声数据较为敏感,因为 SVM 是通过 最大化支持向量与决策边界的间隔 来进行优化的。如果存在噪声样本,这些噪声样本可能会成为支持向量,从而影响到决策边界的位置。
• 为了解决这个问题,SVM 引入了 软间隔(Soft Margin) 和 惩罚参数 C ,允许模型对一些样本进行误分类,但会对这些误分类样本进行一定的惩罚。
5. 处理多分类问题
• 逻辑回归:
• 逻辑回归可以轻松扩展到多分类问题,使用 一对多(One-vs-Rest, OvR) 或 多项式逻辑回归(Softmax Regression) 来实现多分类任务。
• SVM:
• SVM 是 二分类算法,需要通过 一对多(OvR) 或 一对一(One-vs-One) 的方式扩展到多分类问题。因此,SVM 在处理多分类问题时相对复杂,需要训练多个分类器。
6. 决策边界与泛化能力
逻辑回归的决策边界:
-
逻辑回归的决策边界是通过概率阈值来确定的。例如,假设我们将 ( 0.5 ) 作为阈值,那么模型的决策边界是使预测概率等于 ( 0.5 ) 的那条直线。
-
优点:简单易懂,适合线性问题。
-
缺点:如果数据线性不可分,逻辑回归的表现会非常差。
SVM 的决策边界:
-
SVM 的决策边界是通过 最大化支持向量与超平面之间的间隔 来确定的。SVM 不仅要正确分类样本,还要保证边界的稳定性。
-
优点:SVM 的最大间隔策略使得它在应对新样本时具有更好的 泛化能力,特别是在高维空间中,SVM 能够有效处理复杂问题。
-
缺点:对于噪声敏感,因为支持向量是影响决策边界的关键,噪声点可能成为支持向量,影响分类效果。
7. 优缺点对比
| 算法 | 逻辑回归 | SVM |
|---|---|---|
| 核心思想 | 基于概率的模型,输出概率值 | 基于最大化间隔,找到最优的决策边界 |
| 决策边界 | 线性决策边界,通过设定阈值确定分类 | 最大化分类间隔的超平面,确保支持向量离边界最远 |
| 非线性处理 | 需要手动扩展特征 | 核方法自动将数据映射到高维空间,处理非线性问题 |
| 概率输出 | 输出类别的概率值,适合需要概率判断的任务 | 仅输出类别标签,不提供概率值 |
| 噪声处理 | 对噪声较为鲁棒 | 对噪声敏感,可能会受支持向量影响 |
| 多分类处理 | 容易扩展为多分类(通过 Softmax 或 One-vs-Rest 方法) | 二分类模型,需要 One-vs-One 或 One-vs-Rest 进行扩展 |
| 泛化能力 | 泛化能力较好,适合线性可分或近似线性可分的数据 | 在高维和复杂非线性数据中有更强的泛化能力 |
8. 如何选择 SVM 和 逻辑回归?
选择逻辑回归的情况:
-
数据是线性可分 或接近线性可分,数据的类别可以通过一条直线或一个超平面分割开来。
-
需要概率输出,例如在一些医疗诊断、金融风险评估中,概率值的输出可以提供额外的信息。
-
数据集较大 且模型训练时间有限,逻辑回归的计算效率较高,尤其是当数据集较大时。
-
特征维度较低,逻辑回归在低维空间中的表现较好。
选择 SVM 的情况:
-
数据是线性不可分,或者数据的类别之间有复杂的边界。SVM 通过核函数可以处理非线性问题。
-
高维数据集,尤其是当特征维度远大于样本数量时,SVM 的表现通常非常好。
-
噪声较少 或你可以通过设置适当的惩罚参数 ( C ) 来控制模型对噪声的容忍度。
什么时候使用 SVM?
1. 数据线性不可分:
• 如果你的数据在原始空间中 线性不可分,SVM 的 核方法 可以有效地将数据映射到高维空间,在高维空间中实现线性分割。这是逻辑回归所不能轻松解决的问题。
2. 需要更好的泛化能力:
• SVM 通过最大化分类间隔来保证模型的 泛化能力,尤其是在样本数较少且特征维度较高的情况下,SVM 通常能够表现得非常好。
3. 对分类边界的要求更高:
• 如果你需要一个 非常明确的决策边界,并且希望分类边界能够最大化不同类别的分隔距离,SVM 是一个更好的选择。
4. 特征维度高且数据量中等:
• SVM 在处理高维数据时效果很好,尤其是在特征数量远多于样本数量的情况下。
什么时候使用逻辑回归?
1. 需要概率输出:
• 如果你不仅关心分类结果,还需要知道模型预测某个样本属于某个类别的 概率,那么逻辑回归是更好的选择。SVM 只能输出类别标签,而不能输出概率。
2. 数据线性可分或接近线性可分:
• 如果你的数据在原始特征空间中本来就是 线性可分的,逻辑回归通常能够很好地解决问题,训练速度快且效果好。
3. 处理噪声较多的数据:
• 逻辑回归对噪声数据较为鲁棒,因为它会基于概率分布进行分类,即使有一些噪声样本,也不会对模型的整体决策边界产生重大影响。
4. 多分类任务:
• 如果你面临的是一个 多分类任务,逻辑回归可以通过扩展(如 Softmax 回归)直接处理,而 SVM 需要训练多个分类器来实现多分类。
总结
• 逻辑回归 是基于概率的分类模型,适用于线性问题或接近线性的问题,并且能够输出类别的概率。在需要解释性或概率判断的任务中,逻辑回归表现更好。
• SVM 是基于最大化分类间隔的模型,能够通过核方法处理复杂的非线性问题。在高维空间中,SVM 通常能够取得较好的泛化效果。特别是在数据线性不可分的情况下,SVM 比逻辑回归更具优势。
相关文章:
比较)
逻辑回归 和 支持向量机(SVM)比较
为了更好地理解为什么在二分类问题中使用 SVM,逻辑回归的区别,我们需要深入了解这两种算法的区别、优势、劣势,以及它们适用于不同场景的原因。 逻辑回归和 SVM 的比较 1. 模型的核心思想 • 逻辑回归: • 基于概率的模型&…...

GS-SLAM论文阅读笔记--TAMBRIDGE
前言 本文提出了一个自己的分类方法,传统的视觉SLAM通常使用以帧为中心的跟踪方法,但是3DGS作为一种高效的地图表达方法好像更侧重于地图的创建。这两种方法都有各自的优缺点,但是如果能取长补短,互相结合,那么就会是…...

[Redis面试高频] - zset的底层数据结构
文章目录 [Redis面试高频] - zset的底层数据结构一、引言二、zset 的底层数据结构1、zset 的编码方式1.1、ziplist 编码1.2、skiplist 编码 1.3、ziplist 编码适用条件1.4、skiplist 编码适用条件2、zset 的操作命令 三、zset 的性能考量1、内存效率2、搜索效率 四、总结 [Redi…...

搜维尔科技:OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作
OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作 搜维尔科技:OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作...

CentOS Linux教程(6)--CentOS目录
文章目录 1. 根目录2. cd目录切换命令3. CentOS目录介绍4. pwd命令介绍5. ls命令介绍5.1 ls5.2 ls -a5.3 ls -l 1. 根目录 Windows电脑的根目录是计算机(我的电脑),然后C盘、D盘。 Linux系统的根目录是/,我们可以使用cd /进入根目录,然后使…...

观察者模式全攻略:从设计原理到 SpringBoot 实践案例
观察者模式 观察者模式(Observer Pattern)是一种行为型设计模式,它定义了一种一对多的依赖关系,使得当一个对象的状态发生改变时,所有依赖于它的对象都能得到通知并自动更新。 核心思想: 观察者模式将**观…...

【MyBatis】Java 数据持久层框架:认识 MyBatis
Java 数据持久层框架:认识 MyBatis 1.CRUD 注解2.映射注解3.高级注解3.1 高级注解3.2 MyBatis 3 注解的用法举例 MyBatis 和 JPA 一样,也是一款优秀的 持久层框架,它支持定制化 SQL、存储过程,以及高级映射。它可以使用简单的 XML…...
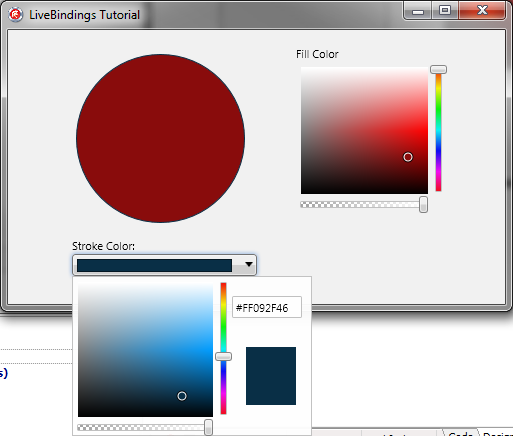
【Delphi】通过 LiveBindings Designer 链接控件示例
本教程展示了如何使用 LiveBindings Designer 可视化地创建控件之间的 LiveBindings,以便创建只需很少或无需源代码的应用程序。 在本教程中,您将创建一个高清多设备应用程序,该应用程序使用 LiveBindings 绑定多个对象,以更改圆…...

深度学习——基础知识
深度学习的重点在于优化,其中很重要的步骤在于如何调参,会涉及到一些微积分等数学知识。不同于以往接触到的数值运算,深度(机器)学习都是关于张量Tensor(向量)的计算,Python中最常用…...

QT实现升级进度条页面
一.功能说明 在Qt中实现固件升级的进度条显示窗口,你可以通过创建一个自定义的对话框(Dialog)来完成。这个对话框可以包含一个进度条(QProgressBar)、一些文本标签(QLabel)用于显示状态信息&am…...

JavaWeb--纯小白笔记04:Tomcat整合IDEA
IDEA整合Tomcat 1.点击Idea的导航栏里的Run,选择Edit Configurations 2.点击左上角的"",向下翻找到Tomcat Server 选择里面的Local 3.创建一个web工程,点击IDEA的File-->new-->project 然后选择Java Enterprise,…...

【jvm】动态链接为什么需要常量池
目录 1. 常量池的作用2. 动态链接与常量池的关系3. 动态链接的必要性 1. 常量池的作用 1.常量池是JVM(Java虚拟机)中用于存储字面量(如字符串常量、整数常量等)和符号引用(如类和接口的完全限定名、字段的名称和描述符…...

HTTPS详解
文章目录 HTTPS加密 常见加密方式对称加密非对称加密非对称对称数据指纹 证书CA认证数字签名非对称证书对称 中间人 HTTPS 这也是一个应用层协议,是在HTTP协议的基础上引入了一个加密层 为什么要加密呢,这主要是因为如果不对传输主体加密,当…...
的缓存)
redis作为mybaits(mybatisplus)的缓存
引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency>配置application.yml文件 spring:data:redis:# 地址host: 127.0.0.1# 端口port: 6379# 数据…...

【环境配置】AST: Asymmetric Student-Teacher Networks for Industrial Anomaly Detection
文章目录 一、环境的配置二、预处理三、训练四、问题 一、环境的配置 # zheP04_cmp_AST $ conda create -n P04_cmp_AST python3.9 $ conda activate P04_cmp_AST $ conda install -y anaconda::scikit-learn $ conda install -y conda-forge::scipy $ conda install -y conda…...

TinkerTool System for Mac实用软件系统维护工具
TinkerTool System 是一款功能全面且强大的 Mac 实用软件,具有以下特点和功能: 软件下载地址 维护功能: 磁盘清理:能够快速扫描并清理系统中的垃圾文件、临时文件以及其他无用文件,释放宝贵的磁盘空间,保…...

物理学基础精解【9】
文章目录 直线与二元一次方程两直线夹角直线方程斜率两点式方程截距式方程将不同形式的直线方程转换为截距方程直线的一般方程直线一般方程的系数有一个或两个为零的直线 参考文献 直线与二元一次方程 两直线夹角 两直线 y 1 k 1 x b 1 , y 2 k 2 x b 2 形成夹角 a 1 和 a…...

Flask-JWT-Extended登录验证
1. 介绍 """安装:pip install Flask-JWT-Extended创建对象 初始化与app绑定jwt JWTManager(app) # 初始化JWTManager设置 Cookie 的选项:除了设置 cookie 的名称和值之外,你还可以指定其他的选项,例如:过期时间 (max_age)&…...

Altium Designer(AD)百度云下载与安装(附安装步骤)
在我们日常使用当中,Altium designer常常也被简称为AD,是一款一体化的电子产品开发系统软件,主要运行在Windows操作系统上。 我们通过Altium designer把原理图设计、电路仿真、PCB绘制编辑、拓扑逻辑自动布线、信号完整性分析和设计输出等技…...

无人机视角下的车辆数据集
车辆数据集 无人机视角下的车辆数据集。数据集为无人机俯拍的真实场景下的车辆机动车数据集。数据集已经标注好,yolo格式,txt标签。数据集已经划分好训练集(20970张图片)验证集(5242张图片)测试集ÿ…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
